台阶式溢洪道流场三维数值模拟研究

郝永志

(新疆水利水电勘测设计研究院，乌鲁木齐 830000)



台阶式溢洪道流场三维数值模拟研究

郝永志

(新疆水利水电勘测设计研究院，乌鲁木齐 830000)

采用VOF法，运用RNG k-ε双方程紊流模型对台阶式溢洪道的水面线、流场、速度场等进行三维数值模拟。研究结果表明：水面线在能量交换过程中受台阶影响先升高再降低；台阶断面上的流速分布符合明渠水流规律；受水体拖拽力和台阶的影响，台阶上的水流分为滑移流和涡旋流两种。通过数值计算和水工试验发现模拟结果与模型试验结果基本相近，说明建立的数学模型及设置的参数模拟台阶式溢洪道的水流特性是可行的。

VOF法；流场；台阶式溢洪道； k-ε紊流模型；数值模拟

1 问题的提出

改革开放以来，随着中国经济的迅猛发展和科学技术水平的不断提高，中国高坝建设取得了前所未有的成就，三峡、双江口、溪洛渡、锦屏等一大批规模巨大的战略型工程拔地而起[1]，这些大型工程普遍存在泄流流量集中、单宽流量大的“高水头、大流量”的特点，其下泄的高速水流对建筑物及下游河床可能造成严重的冲击破坏。为减免混凝土的空蚀破坏，溢洪道设计时要求溢流面光滑，但在高速水流的冲刷下，仍会产生空蚀破坏[2]。除此之外，传统溢洪道的溢流面平整度施工难度大、工期长、造价高、机械化施工困难等弊端。

台阶式溢洪道就是从泄槽段到消力池入口处布置一系列台阶，利用水流与台阶碰撞所产生的横向斡滚与主流之间的剪切作用促进水体表面波破碎使水流掺气，将势能转化为动能，在泄槽段实现能量交换以消除大量能量。相较于传统溢洪道，台阶式溢洪道有其明显优势：①可显著提高溢洪道的消能率，有效缩短消力池长度，简化消能设施；②台阶可以一次碾压成型，省去溢流面二次立模浇筑，施工工序简便，工期大幅缩短，进而降低工程投资[3]。为研究台阶式溢洪道水面线及流场分布规律，引入VOF法的RNG k-ε稳流模型对其进行三维数值模拟来研究台阶式溢洪道的水流特性。

2 模型建立与计算

2.1 物理模型建立

委托西北农林科技大学对表孔溢洪道进行水工模型试验[4]，用水工模型试验成果来验证数学模型选择可靠性和模拟结果的准确性性。该开敞式侧堰表孔溢洪道原型由侧堰段、水平稳流段、泄槽缓坡段、涡曲线段、泄槽陡坡段、渐变段及消力池组成，总长365.607m。根据试验要求，模型设计需要满足几何相似、水流运动相似和重力相似，因此，模型制作遵循佛劳德相似准则并结合实验室场地等条件进行。溢洪道水工模型试验布置见图1。

模型几何比尺Lr=40，流量比尺Qr=Lr5/210119.289，流速比尺vr=Lr1/2=6.3246，时间比尺Tr=Lr1/2=6.3246，糙率比尺nr=Lr1/6=1.8493。渥曲线方程为y=0.164x+0.00663x2。泄槽缓坡段坡度i=1∶6.0796，陡坡段坡度i=1∶2.5022。溢洪道宽度除消力池入口前20m由5m渐变至10m，其余部分均为5m，台阶步长2.5m，步高1.0m，共布设46阶台阶，泄槽渐变段出口与消力池连接。

图1 溢洪道水工模型试验布置图

2.2 数学模型建立

离散方程组的求解采用欠松驰迭代方法，水气两相流的自由表面处理采用VOF(Volume of Fluid)模型[5]，采用标准k-ε模型对模型求解。

对紊流模型数值模拟中，应用k-ε模型。其连续方程、动量方程和k、ε方程表示为：

连续方程：

(1)

动量方程：

(2)

k方程：

(3)

ε方程：

(4)

式中：t为时间，ρ为密度，μ为分子黏性系数；u为速度，x为坐标。模型参数为Cu=0.09，C1ε=1.44，C2ε=1.92，σk=1.0，σε=1.3。

引入VOF模型后，ρ和μ则为体积分数的函数，不再是一个常数，即：

ρ=αwρw+(1+αw)ρa

(5)

μ=αwμw+(1-αw)μa

(6)

式中：ρw和ρa分别为水和气的密度；μw和μa分别为水和气的分子黏性系数。

2.3 模型网格划分及计算边界条件

2.3.1 网格划分

软件的网格划分形式主要为结构化网格、非结构化网格及结构化和非结构化相结合的划分方式，网格生成对CFD至关重要，直接关系到CFD计算问题的成败。采用何种网格划分形式要根据模型的具体形式予以选择。本文建立的台阶式溢洪道模型是矩形以“搭积木”的形式拼搭起来，体型规整，三维网格划分较好；同时水体具有一定的黏滞性，因此本模型采用结构化网格进行划分，避免了非结构化网格填充率低、网格数量大、计算耗时、不能很好地计算水体黏滞性等问题[6]。为方便计算模型建立、缩短计算时间，本文从涡曲线段至消力池入口建立三维数值计算模型(见图2)。模型计算区域网格共划分5.73万个。网格划分见图3。

图2 台阶式溢洪道三维数值模拟空间模型

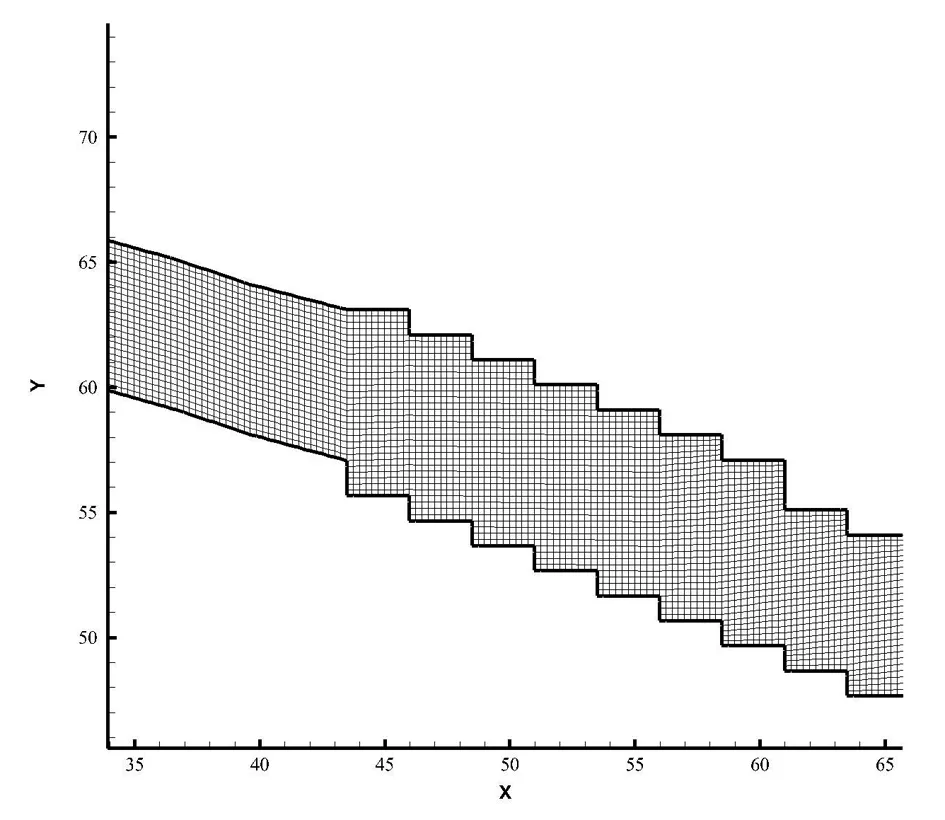
图3 计算网格划分图

2.3.2 边界条件

本模型的计算区域为水、气两种介质。将水体定义为主相，其密度为1000 kg/m3；气体为次相。

进口边界条件为：

ux= V，uy= 0，uz=0

(7)

式中：ux、uy、uz分别为x、y和z方向的分速度，取来流方向为x正向，设置进口流量Q=165.473m3/s，流速V=15.65m/s。

空气进口边界：由于溢洪道表面与大气联通，即将溢洪道顶面设置为压力进口边界，压强设置为0。

出口边界：装置的出口分别为下游河道流速出口与空气出口，由于下游河道水深要求，故将水流出口设置为速度出口边界。取来流方向为x正向，：ux=U，uy= 0，uz=0；，故设置出口流速为U=-2.55 m/s。

压力出口边界：溢洪道下游水流出口上方与大气接触，设置为压力出口边界，供溢洪道上层空气流出，出口压强设置为0。

固壁边界条件：溢洪道底面与变比均为固壁边界，采用无滑移边界条件，并使用标准壁面函数法确定固壁附近的流动。

3 计算结果对比及分析

3.1 自由水面线

通过三维数值模拟计算得到了台阶上部水流达到稳定时的自由水面线，图4是溢洪道台阶上部自由水面线图。由图4可以看出，渥曲面段至1#台阶水流流态是滑行流[7]；从1#台阶开始，溢洪道底部不再是光滑平面，底部水流受阶梯干扰，开始出现波动，1#、2#台阶受上游滑行流影响，底部水流波动轻微，从3#台阶表面开始水流波动逐渐加剧，底部水流与上部水流发生脱流现象，形成水汽两相流，随着台阶表面水滴跃离现象剧烈，水面开始逐渐上升。随着水流的势能不断转化成动能，水体的动能>阶梯对水流的摩阻作用所损失的能量[8]，水流流速沿程增大，自由水面线开始降低。由图5可以看出，泄槽陡坡段水流在台阶作用下紊动强度达到一定峰值后，阻力作用<水体动能，水面线开始降落。由图5还可以看出，水面线试验结果与数值计算结果基本吻合，过渡区域内水流涡旋最剧烈，水面线最高，过渡区域基本发生在泄槽陡坡段中部。

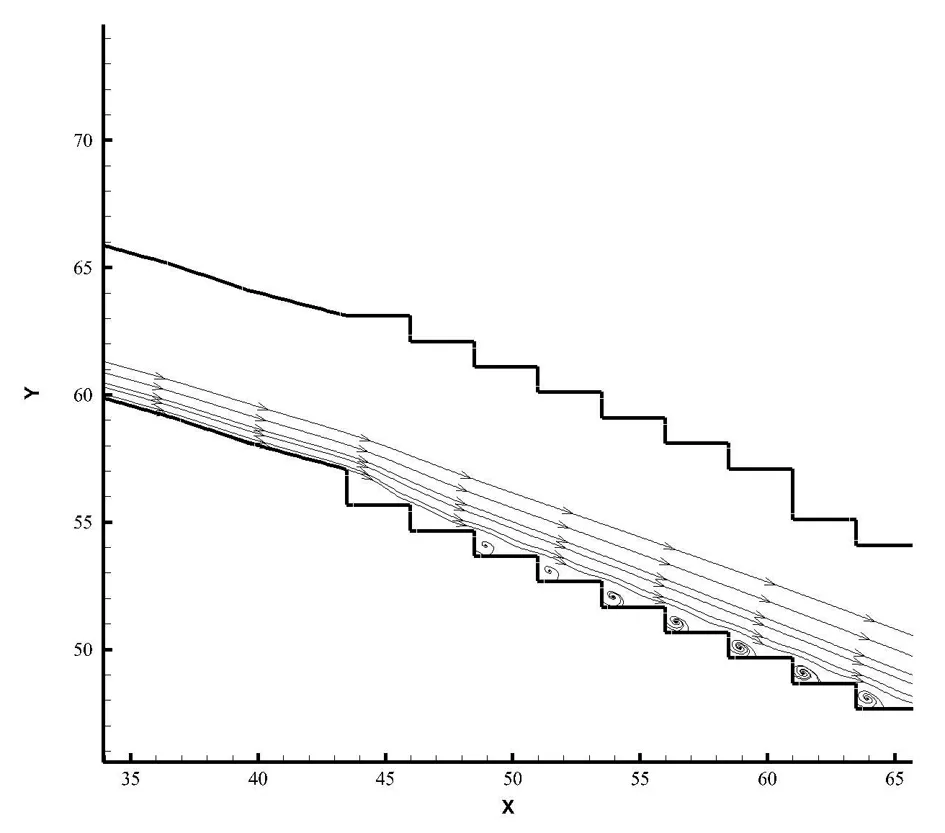
图4 台阶式溢洪道上部自由水面线图

图5 自由水面线模拟计算值与试验值对比表

3.2 断面流速分布

为了更好的研究台阶式溢洪道流速分布情况，现以典型断面台阶凸角处垂直于虚拟光滑溢流面方向的流速分布如图6所示。由图6可看出，台阶凸角上的流速分布与光滑溢流面上的流速分布规律相似，也是在接近底板处流速近似为0，沿水深方向流速逐渐增大，达到最大值后稍有减小，该规律符合明渠水流流速分布规律。台阶式溢洪道流速分布从凸角处沿虚拟底板垂直方向逐渐增大，流速梯度较大，迅速增加到势流流速，随后流速稍有变化，但此时受主流区滑移流的影响，流速变化幅度较小[9]。本文选取首端、中端和末端(即取5#台阶、20#台阶和38#台阶)为典型断面进行流速分析，3个断面的流速值与自由水面线分布规律一致。5#台阶为紊流起始点，受渥曲面段滑移流影响，流速较大；随着紊动强度增大，大部分势能转化为动能，水气两相流涡旋耗散较多动能，流速略有减小；当摩阻作用小于水流的动能后，流速又开始增大。台阶式溢洪道的水流在不断的能量交换过程中起到了显著的消能效果[10]。

5#台阶 20#台阶 38#台阶

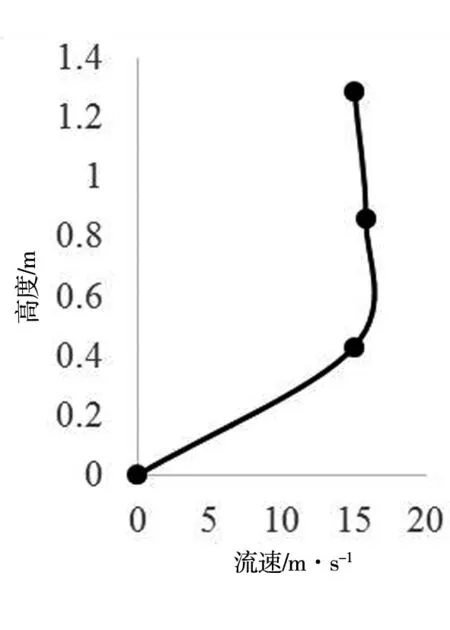
3.3 速度场

图7为数值模拟计算得到的台阶内部漩涡图，图8为水工模型试验得到的台阶内部漩涡图。从图7和图8可以明显看出，在台阶水平步长、铅直步长和凸角连线构成了一个虚拟封闭的三角形漩涡区[11]，在每个漩涡区内均有一顺时针方向旋转的涡旋流，涡旋流中心处流速接近零，向四周扩散，流速逐渐增大，但由于水体具有黏滞性，漩涡区流速小于凸角连线处滑行流。滑移流速度等值线与台阶虚拟底板近似平行。由图4和图8可以看出，由于渥曲面段流速较大，以滑移水流为主，同时1#、2#台阶的水平步长较短，在台阶起始端并没有形成涡旋流，但1#、2#台阶的加糙作用，从3#台阶开始逐渐有滑移流水流发生脱流，流速逐渐减小，涡流区内掺气逐渐增多，水流的紊动强度越来越剧烈，由于水流的拖拽作用，形成上部以滑移流为主、底部漩涡区内以涡旋流为主的两种流态。

图7 数值计算台阶内部漩涡图

4 结 论

文章采用VOF法的RNG k-ε双方程紊流模型对台阶式溢洪道进行三维数值模拟[12]，通过数值模拟计算和水工模型试验对比分析发现两者得到的结果基本一致，说明RNG k-ε紊流模型能够很好地对台阶式溢洪道复杂流场进行三维数值模拟，VOF模型能够真实准确地对水气两相流临界面迭代求解，是模拟求解水面线和流态的理想方法。

[1]贾来飞.溢洪道掺气坎槽后掺气水流三维数值模拟研究[D].天津：天津大学,2012.

[2]张峰.台阶式溢洪道消能特性的研究[D].西安：西北农林科技大学,2014.

[3]尹芳芳.带有掺气挑坎的台阶式溢洪道的三维数值模拟[D].西安：西安理工大学,2010.

[4]西北农林科技大学.新疆哈拉吐鲁克水库表孔溢洪道水工模型试验报告[R].西安：西北农林科技大学，2015.

[5]惠康,邱秀云,陶洪飞,等.基于加压液化输沙技术的浑水水力分离清水装置中水沙两相三维流场数值模拟[J].水电能源科学,2014(08):120-122+94.

[6]靳晟,李琳.基于数值模拟的某阶梯溢洪道方案优化研究[J].水资源与水工程学报,2013(05):17-22.

[7]杨吉健,刘韩生,代述兵,等.台阶式溢洪道阶顶过流断面平均流速沿程变化研究[J].水力发电学报,2015(06):107-111.

[8]田嘉宁,大津岩夫,李建中,安田阳一.台阶式溢洪道各流况的消能特性[J].水利学报,2003(04):35-39.

[9]〗张志昌,曾东洋,刘亚菲.台阶式溢洪道滑行水流水面线和消能效果的试验研究[J].应用力学学报,2005(01):30-35+157.

[10]〗张为法,刘韩生.斯木塔斯台阶式陡槽溢洪道水力特性模型试验研究[J].中国农村水利水电,2011(01):93-96.

[11]何照青,祁永斐,李卫鹏.基于VOF模型的阿拉沟溢洪道流场数值模拟[J].水资源与水工程学报,2013(02):170-173.

Experimental Study on 3D numerical simulation of Stepped Spillway Flow Field

HAO Yong-zhi

(Xinjiang Water Conservancy and Electricity Survey and Designing Institute，Urumqi 830000，China)

Direct with the RNG k-ε double-equation turbulence mode，which was introduced by the method of VOF，3D numerical simulation were conducted to simulate free surface，flow field，velocity distributions of stepped spillway. The results show that free surface increased at first and then decreased because the effect of step when energy exchange; velocity distribution law of sidestep section accord with open channel flow; water flow was divided into two flow state which were slip flow and vortex flow because the influence on water drag force and step. Through the numerical calculation and hydraulic test found that simulation results and test results were basically identical，the paper show that mathematical model and parameters is feasible to simulate flow characteristics of stepped spillway.

VOF method; flow field; stepped spillway; k-ε turbulence mode; numerical simulation

TV651.1；TV135.2

B

1007-7596(2016)08-0008-03

2016-07-14

胡静(1985-)，女，江西南昌人，工程师，从事工程造价和水工建筑物施工工作。