利用ARMA模型预报电离层总电子含量研究

文/刘贵云 湖南省地质测绘院 湖南衡阳 421001

利用ARMA模型预报电离层总电子含量研究

文/刘贵云 湖南省地质测绘院 湖南衡阳 421001

利用IGS中心的电离层TEC数据作为实验数据，采用ARMA模型对TEC进行建模预报，并对对该模型的预报精度与BP神经网络进行对比分析，实验结果表明：ARMA模型的预报精度较为稳定，能更好地反映TEC变化趋势。

总电子含量；ARMA模型；BP神经网络；精度分析

1.引言

电离层延迟一直是GNSS定位的主要误差来源，对卫星的导航定位精度产生严重的影响，因此，需要对电离层延迟误差进行修正。电离层延迟误差主要受传播路径上的总电子含量（Total Electron Content， TEC）影响[1］，而对TEC的研究一直是国内外的研究热点，并取得了一定的研究成果。现今，常用电离层TEC预报模型有球谐模型[2］、Klobuchar模型[3］等，文献[2］基于球谐函数模型的基础上，采用时间序列分析模型进行预报，其预报精度有了较大的提高，但模型计算较为复杂，而文献[3］提出的改进Klobuchar模型计算简便，基于广播星历所提供的8参数即可解算TEC，并对模型的初始相位、振幅和夜间时延值进行改进，从而提高了模型的预报精度，但该模型是根据长期的观测资料建立的，因此模型精度仍有待提高。针对以上问题，国内外的学者基于TEC数据的非线性、非平稳特性，提出了格网模型[4］、时间序列模型[5］、神经网络模型[6］等，并取得了一定的效果。因此，本文采用时间序列模型对处于不同时空环境的电离层TEC数据进行建模预报，并与BP神经网络对比，重点分析两种模型的预报精度。

2. ARMA模型算法原理

ARMA（Auto Regressive and Moving Average）模型时间序列分析法是一种利用参数模型对有序随机振动响应数据进行处理，从而进行模态参数识别的方法，参数模型包括AR自回归模型、MA滑动平均模型和ARMA自回归滑动平均模型。

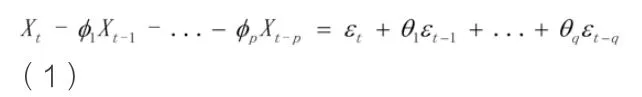
则式（9）可表示为：

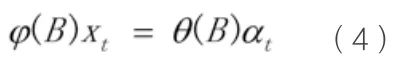
3.算例分析

3.1 数据来源与精度评估

本文采用数据来源于IGS中心提供的电离层TEC数据进行实验，其空间分辨率为 ，时间分辨率为2 h，利用BP神经网络模型和ARMA模型对不同时空环境下的TEC数据分别进行建模预报，并以IGS中心发布的TEC值作为真值，利用相对精度和平均绝对偏差来评估两种模型的预报精度：

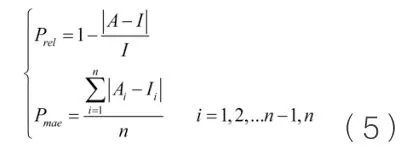
式中，A为模型预报的TEC值；I为IGS中心发布的TEC值；n为TEC值预报量。

3.2 模型在不同环境下的预报精度分析

任意选取IGS中心提供的格网点（30°N、120°E）在2014年年积日分别为1～10日，100～110日，200～210日，300～310日 的TEC值作为实验数据，且这4个时段包含了电离层活跃期和平静期。采用BP神经网络模型和ARMA模型分别对各个时段前7 d的TECu值预报后3 d的TEC值，并与真值进行精度对比分析。

预报结果如图2所示，图2中共4个子图，分别为不同时段的预报结果图，横坐标表示预报的历元数，3 d共36个历元，纵坐标表示TEC值，单位为TECu，红色十字形代表BP神经网络模型预报的TEC值，蓝色星形代表ARMA模型预报的TEC值，绿色圆形代表IGS提供的TEC值。由图2可得出：（1）在不同时间环境下，BP神经网络模型和ARMA模型的预报值与真值均符合得很好，其预报精度都较高；（2）两种模型在TEC极值处的历元预报偏差较大，但ARMA模型略优于BP神经网络模型。

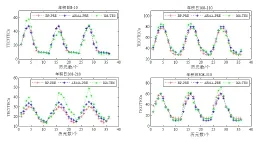
图1 不同模型在不同环境预报精度对比分析

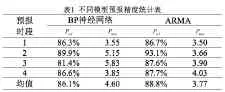
为了更进一步分析BP神经网络模型和ARMA模型在不同环境下的预报精度，本文将两种模型的预报相对精度以及平均绝对偏差进行统计分析研究，如表1所示。由表1可以得出：（1）在不同的预报时段，两种模型的预报相对精度都优于80%，且在各个时段ARMA模型的精度由于BP神经网络模型；（2）在不同的时段，ARMA模型的平均绝对偏差小于BP神经网络模型；（3）ARMA模型在各个时段的预报精度相对稳定，而BP神经网络模型的预报精度波动比较大。综上所述，两种模型的预报精度整体都较高，但ARMA模型更能准确地预报TEC的变化趋势。

4.结论

本文采用IGS中心提供的4个不同时段的高精度电离层TEC数据进行实验，利用ARMA模型进行建模预报，并与BP神经网络模型进行了对比分析，根据大量的实验分析表明：

（1）ARMA模型模型的预报精度都较高，都能较好地反映TEC的变化特性，平均绝对偏差为3.77 TECu；

（2）ARMA模型的预报精度略优于BP神经网络模型，且ARMA模型的预报精度更为稳定可靠

由于本文所采用的数据有限，同时电离层的时空变化特性比较复杂，因此ARMA模型在其他时空环境的适用性有待进一步研究。

致谢 衷心感谢IGS中心提供电离层TEC格网数据！

[1］范国清，王威，郗晓宁.基于广义回归神经网络的电离层VTEC建模[J］.测绘学报，2010，01：16-21.

[2］周伟莉，李素华，蒋美霞.基于球谐函数模型的电离层预报[J］.测绘信息与工程，2012，03：3-5.

[3］蔡成辉，刘立龙，黎峻宇，林国标.基于改进的Klobuchar模型建立南宁市区域电离层延迟模型[J］. 大地测量与地球动力学，2015，05：797-800.

[4］刘军，柴洪洲，范龙，王海栋.基于格网的GPS/BD-2组合系统电离层VTEC模型研究[J］.测绘科学，2011，03：34-36.

[5］汤俊，姚宜斌，陈鹏，利用EMD方法改进电离层TEC预报模型[J］.武汉大学学报（信息科学版）， 2013， 38（4）： 408-411.

[6］张禄.基于时间序列、神经网络、灰色和组合预测对电离层TEC的预测研究[D］.南京信息工程大学，2012.

[7］谢迎涛.基于MATLAB人工神经网络预测太阳耀斑级别的研究[D］.河南师范大学，2014.

[8］Shumway R H， Stoffer D S. Time series analysis and its application[M］. New York： Springer-Verlag，2000.