基于全局灵敏度分析的侧向气动导数不确定性对侧向飞行载荷的影响

阮文斌， 刘洋， 熊磊

上海飞机设计研究院 总体气动部， 上海　201210



基于全局灵敏度分析的侧向气动导数不确定性对侧向飞行载荷的影响

阮文斌*， 刘洋， 熊磊

上海飞机设计研究院 总体气动部， 上海201210

考虑飞行载荷计算中使用的气动导数存在不确定性，利用基于方差的全局灵敏度分析(GSA)方法，结合偏航机动的动力学模型，分析了侧向气动导数不确定性对侧向飞行载荷的影响。以某型飞机为例，运用该方法得到侧向气动导数的全局灵敏度排序。结果表明：侧滑角、阻尼贡献的垂尾侧向载荷及垂尾侧向总载荷受全机侧力系数对侧滑角导数的影响最大，受航向静稳定导数及方向舵操纵效能的影响次之；方向舵偏度贡献的垂尾侧向载荷只受全机侧力系数对方向舵偏度导数的影响；无尾飞机侧向载荷主要受航向静稳定导数、方向舵操纵效能及无尾飞机侧力系数对侧滑角导数的影响；偏航阻尼导数基本不影响各侧向飞行载荷。同时也验证了方法的有效性，对提高飞行载荷的计算精度有一定的指导意义。

全局灵敏度分析； 不确定性； 气动导数； 飞行载荷； 方差； 偏航机动

飞行载荷是评定飞机在使用寿命期间结构完整性的原始数据，其合理性、精确性对保证飞机的使用安全、减轻结构重量、实现设计性能和保证经济服役寿命至关重要。作为飞行载荷设计工程师,必须找出飞机各部件最大飞行载荷,并给出飞行载荷的大小和分布,以此作为飞机结构强度的设计依据。在飞行载荷的计算过程中，很多因素直接或间接影响飞行载荷的计算精度，如结构柔性、非线性气动力特性、飞行控制律、推力矢量和飞机弹性变形等。因此，开展飞行载荷计算影响因素的研究具有重要的意义和工程价值。

目前，国内外关于上述相关工作的研究有很多，主要着重于飞行载荷设计方法和对适航条款的理解，如文献[1-3]研究了柔性飞机的非线性飞行载荷计算，文献[4]研究了飞机操纵系统特性对机动载荷的影响，文献[5]研究了民用飞机阵风载荷及减缓技术，而缺乏对载荷计算输入不确定性的影响研究。气动导数作为飞行载荷计算的重要输入之一，由于风洞试验[6]、工程估算[7]和数值计算等误差，以及线性化理论[8]的简化，造成其存在较大随机不确定性[9]，进而使得输出载荷也具有不确定性。因此，为了提高飞行载荷计算精度，有必要研究气动导数输入不确定性对输出载荷不确定性的影响。然而，目前国内外在相关领域的研究较少，仅文献[10-11]研究了气动导数变化对飞行品质的影响，且将气动导数视为非随机变量，而多数情况下气动导数不确定性具有随机分布的特点[9]，将其视为随机型变量能得到更丰富的输出分布信息。

近年来，国内外相关研究者发展了一种新的灵敏度分析方法，即全局灵敏度分析(GSA)方法，该方法因从整体上分析输入变量不确定性对输出响应量的影响而应用尤为广泛[12-18]，并已形成三大类：非参数方法[12-13]、基于方差的分析方法[14]以及矩独立分析法[15]。其中，由于基于方差的分析方法能够直接反映输入变量对输出响应量方差(即不确定性)的贡献并且容易计算, 加上方差是工程实践中最关心的统计特征量,因此该方法在许多领域已得到了广泛应用[16-18]，并验证了其有效性。但目前该全局灵敏度分析方法在飞行载荷中的应用却几乎没有，在该领域得到的分析结果是否有效也并未得到验证。

为此，本文采用基于方差的全局灵敏度分析方法，结合飞机偏航机动动力学模型，将侧向气动导数视为随机输入变量，各部件侧向飞行载荷视为输出响应量，建立了侧向飞行载荷对侧向气动导数的全局灵敏度指标及求解方法。通过对某型飞机算例计算，分析了侧向气动导数不确定性对侧向飞行载荷的影响；同时验证了由该种全局灵敏度分析方法所得结果的合理性和有效性。

1　偏航机动侧向飞行载荷的求解

偏航机动是中国民用航空规章第25部(CCAR-25-R4)[19]条款§25.351规定的重要设计情况。机动中因飞机产生侧滑，造成飞机不对称受载，方向舵偏转和侧滑导致垂尾承受很大载荷，该情况是垂尾、后机身的主要受载情况。

按规范定义考虑偏航机动时，飞机响应可用侧滑及偏航二自由度方程描述, 即

(1)

初值为：t=0时，β=a=0。式中：β为侧滑角；t为时间；g为重力加速度；q为速压；S为机翼面积；W为全机重；V∞为无穷远处来流速度；CCβ为全机侧力系数对侧滑角的导数；CCTOβ为无尾飞机侧力系数对侧滑角的导数；a为偏航角速度；Lv为垂尾对重心的尾力臂；CCδr为全机侧力系数对方向舵偏度的导数；δr为方向舵偏度；b为机翼展长；Iz为偏航转动惯量；Cnβ为全机偏航力矩系数对侧滑角的导数,也称航向静稳定导数；Cna为全机偏航力矩系数对偏航角速度的导数,也称偏航阻尼导数；Cnδr为全机偏航力矩系数对方向舵偏度的导数,也称方向舵操纵效能；M为全机重心处纵向坐标；M0为气动力力矩参考点纵向坐标。

CCAR-25-R4条款§25.351规定了在计算垂尾载荷时可以假定偏航角速度为零，最大方向舵偏度的大小及δr-t操纵规律。然后，按式(1)求出整个过程的β和a响应，可得垂尾侧向总载荷Fv为

Fv=Fvβ+Fvδr+Fva

(2)

(3)

Fvδr=CCδrδrqS

(4)

(5)

式中：Fvβ为侧滑角贡献的垂尾侧向载荷；Fvδr为方向舵偏度贡献的垂尾侧向载荷；Fva为阻尼贡献的垂尾侧向载荷。

无尾飞机侧向载荷FTO为

FTO=CCTOββqS

(6)

本文选择飞机响应过程中垂尾侧向总载荷Fv达到最大瞬时为设计点,以气动导数CCβ、CCTOβ、CCδr、Cnβ、Cna和Cnδr为随机输入变量，Fvβ、Fvδr、Fva、Fv和FTO为输出响应量，利用基于方差的全局灵敏度分析方法，分别分析各气动导数的不确定性对该设计点处飞行载荷的影响。

2　全局灵敏度分析

在众多全局灵敏度分析方法中，基于方差的方法由于能够直接反映输入变量对输出响应量的影响并且容易计算，且运用尤为广泛，因此，本节将该方法应用于飞机飞行载荷的影响研究。

2.1基于方差的全局灵敏度分析

假设X=[X1X2…Xn]包含n个独立的随机输入变量，本文中X为侧向气动导数，ψ(X)为第1节定义的飞机载荷响应函数。由Sobol[14]提出的基于方差的方法，可在飞机各部件结构中建立载荷输出响应ψ(X)对气动导数Xi的全局灵敏度指标为

(7)

式中：算子V(·)和E(·)分别为求方差和期望；Si(i=1,2，…,n)为一阶灵敏度指标(也称气动导数Xi对载荷输出响应ψ方差贡献的“主效应”)，该指标可用于衡量Xi对ψ方差的单独贡献,能够反映Xi的不确定性对ψ的影响。由式(7)可知，0≤Si≤1，Si的值越大，表明Xi对ψ的影响越大，进而可通过有针对性的实验或仿真等手段来减小Xi的不确定性，从而提高ψ的精度。反之，若Si的值趋近于0，则说明Xi对ψ几乎没有影响，可对Xi放宽要求，进而提高工作效率。

2.2全局灵敏度指标的求解

由式(7)定义的全局灵敏度指标可知，求解该指标的难点在于计算响应函数的条件期望的方差。求解条件期望的通用方法是MonteCarlo数值模拟[20],但其致命的弱点是计算工作量非常大，需要抽取大量的样本数据才能达到精度要求，以至于该方法在实际工程问题中很难应用。目前，工程实际中在计算全局灵敏度指标方面更为普遍的一类方法为基于模型拟合的方法，如移动最小二乘(MovingLeastSquares,MLS)法[17]和状态依存参数(StateDependentParameter,SDP)法[21]等。由于这些方法都已发展比较成熟，有些直接调用MATLAB软件工具箱就可以得到相应的结果，因此本文对这些方法不再具体说明。

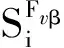
步骤1根据气动导数的统计特性，利用MATLAB软件产生样本量为N的随机输入样本矩阵A：

(8)

步骤2利用步骤 1中生成的随机输入样本，运用MATLAB软件求解式(1)和式(3)得到N个对应的载荷响应量值Fvβ,j(j=1,2，…,N)。进而得到Fvβ的总方差估计值V(Fvβ)为

(9)

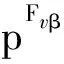
(10)

(11)

3　侧向气动导数不确定性对侧向飞行载荷的影响

本节采用第1节定义的偏航机动动力学模型，以某型飞机原始数据为基础，考虑侧向气动导数为随机输入变量，计算了各部件侧向飞行载荷，进而应用第2节讨论的全局灵敏度分析方法，分析了侧向气动导数不确定性对侧向飞行载荷的影响。假定气动导数都服从正态分布，变异系数均为0.06，且互不相关。

首先由MATLAB软件根据气动导数的分布参数产生一组样本量N为1 000的随机样本；然后利用侧向飞行载荷计算方法求得相应的1 000个输出载荷的值；最后运用全局灵敏度分析方法及求解步骤得到侧向飞行载荷对气动导数的全局灵敏度指标值，所得结果见图 1。分析图 1全局灵敏度指标计算结果可知：

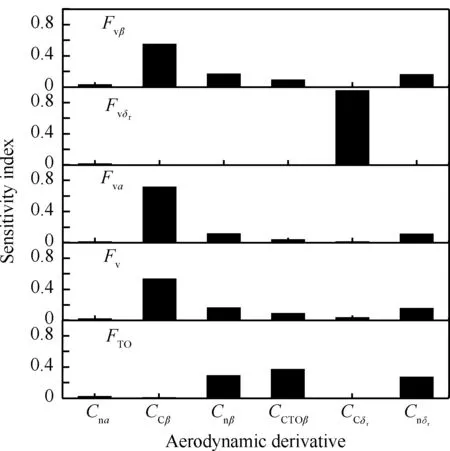
图1　侧向飞行载荷对侧向气动导数的灵敏度指标值Fig.1　Sensitivity index of side flight load to side aerodynamic derivatives　

1) 偏航阻尼导数Cna对应的指标值几乎都为0，表明Cna的不确定性基本不影响各侧向飞行载荷。

2) 侧滑角贡献的垂尾侧向载荷Fvβ、阻尼贡献的垂尾侧向载荷Fva和垂尾侧向总载荷Fv对全机侧力系数对侧滑角的导数CCβ的指标值都很大，而方向舵偏度贡献的垂尾侧向载荷Fvδr和无尾飞机侧向载荷FTO对CCβ的指标值几乎为0，这表明载荷Fvβ、Fva和Fv对CCβ很敏感，Fvδr和FTO对CCβ不敏感。当要提高Fvβ、Fva和Fv的精确度时，应该着重考虑CCβ，尽量提高该气动导数的精度要求，减少它的随机不确定性(即减小变异系数)，而当考虑提高Fvδr和FTO的精度时，降低CCβ的不确定性是无效的。

3) 当提高Fvβ、Fva和Fv的精确度时，还能减少航向静稳定导数Cnβ和方向舵操纵效能Cnδr的不确定性。

4) 当要提高Fvδr的精确度时，只能减少全机侧力系数对方向舵偏度的导数CCδr的不确定性。

5) 减少Cnβ、Cnδr和无尾飞机侧力系数对侧滑角的导数CCTOβ的不确定性都能提高FTO的精确度。

从上述分析可知，各侧向飞行载荷对Cna的灵敏度都很低，这是由于Cna为动导数，而本文所讨论的载荷都为静载荷；由式(4)中定义的载荷Fvδr可以看出，该载荷只与气动导数CCδr有关，因此Fvδr只受CCδr的不确定性影响。这表明上述应用基于方差的全局灵敏度分析方法所得结论是合理的，符合实际的。

另外，为了进一步验证由基于方差的全局灵敏度分析方法所得结论的正确性和有效性，本文考察了气动导数的变异系数(即不确定性)变化时，各侧向飞行载荷变异系数的变化情况。气动导数的变异系数变化范围为-40%～40%，图2(a)显示了Fvδr的变异系数随侧向气动导数参数变化的情况。由图2(a)可见，Fvδr的变异系数随CCδr的变异系数变化而变化的程度很明显，除此之外，单独将其他气动导数的变异系数按同比例改变大小时，发现Fvδr的变异系数几乎没有变化，这证实了上述分析结果是正确的。进一步通过计算验证发现，单独将CCδr的变异系数减少40%时，Fvδr的均值为172 183.25N，变异系数为0.037。与原参数情况对比，发现Fvδr的均值几乎没有改变，而Fvδr的变异系数则降低了35.96%。

类似的，由图2(b)可见，FTO的变异系数随Cnβ、CCTOβ和Cnδr的变异系数变化而变化的程度都比较显著。通过计算验证发现，单独减小Cnβ、CCTOβ和Cnδr的变异系数40%时，FTO的变异系数分别减少了9.56%、15.24%、10.13%。除此之外，单独将其他气动导数的变异系数按同比例改变大小时，发现FTO的变异系数几乎没有变化，这也证实了上述分析结果是正确的。

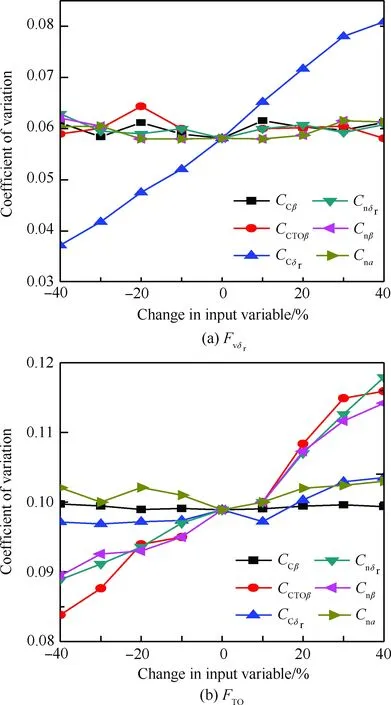
图2　侧向飞行载荷变异系数随侧向气动导数的变化Fig.2　Coefficient of variation of side flight load varying with side aerodynamic derivatives

4　结　论

1) 基于方差的全局灵敏度分析方法可以适用于分析飞行气动导数随机不确定性对侧向飞行载荷的影响，分析结果是正确有效的。

2) 各飞行气动导数的不确定性对飞机不同部件侧向飞行载荷的影响是不一样的：Cna几乎不影响各侧向载荷；Fvδr只受CCδr的影响；CCβ对Fvβ、Fva和Fv的影响最大，Cnβ、Cnδr次之；Cnβ、CCTOβ及Cnδr对FTO的影响都很大。

[1]邓立东, 李天, 薛晓春. 飞机非线性飞行载荷计算方法研究[J]. 航空学报, 2002, 23(4): 317-320.

DENG L D, LI T, XUE X C. Calculation method about non-liner flight loads of aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2002, 23(4): 317-320 (in Chinese).

[2]邓立东, 李天. 柔性飞机的非线性飞行载荷计算研究[J]. 飞行力学, 2004, 22(4): 85-88.

DENG L D, LI T. Research of nonlinear flight loads calculation on a flexible aircraft[J]. Flight Dynamics, 2004, 22(4): 85-88 (in Chinese).

[3]潘登, 吴志刚, 杨超, 等.大柔性飞机非线性飞行载荷分析及优化[J]. 航空学报, 2010, 31(11): 2146-2151.

PAN D, WU Z G, YANG C, et al. Non-liner flight load analysis and optimization for large flexible aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(11): 2146-2151 (in Chinese).

[4]王仲燕. 飞机操纵系统特性对机动载荷的影响[J]. 航空学报, 1994, 15(1): 27-31.

WANG Z Y. The influence of airplane control system properties on the maneuver loads[J]. Acta Aeronautica et Astronautica Sinica, 1994, 15(1): 27-31 (in Chinese).

[5]赵继伟, 胡赞远. 民用飞机阵风载荷及减缓技术的研究[J]. 民用飞机设计与研究, 2012, 104(1): 17-20.

ZHAO J W, HU Z Y. Research on gust load and its load alleviation technology of civil aircrafts[J]. Civil Aircraft Design & Research, 2012, 104(1): 17-20 (in Chinese).

[6]徐林程, 王刚, 武洁, 等. 翼型风洞试验中不确定性分析的自动微分方法[J]. 航空学报, 2014, 35(8): 2102-2111.

XU L C, WANG G, WU J, et al. Uncertainty analysis of airfoil wind tunnel tests with automatic differentiation[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(8): 2102-2111 (in Chinese).

[7]谭林林, 王正平, 刘军. 飞翼布局横航向气动导数的总体估算研究[J]. 飞行力学, 2009, 27(2): 16-19.

TAN L L, WANG Z P, LIU J. Analyzing lateral and directional static derivatives of flying wing based on conceptual design[J]. Flight Dynamics, 2009, 27(2): 16-19 (in Chinese).

[8]李鹏, 顾宏斌, 高振兴. 三次样条插值法在气动导数计算中的应用[J]. 飞行力学, 2008, 26(2): 74-76.

LI P, GU H B, GAO Z X. Application of thrice spline method in the calculation of aerodynamic derivatives[J]. Flight Dynamics, 2008, 26(2): 74-76 (in Chinese).

[9]王贵东, 陈则霖, 刘子强. 飞行器气动参数估计不确定度评价方法研究[J]. 航空学报, 2013, 34(9): 2057-2063.

WANG G D, CHEN Z L, LIU Z Q. Study on uncertainty evaluation methods of aerodynamic parameter estimation for aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(9): 2057-2063 (in Chinese).

[10]胡朝江. 飞机纵向飞行品质对大迎角气动导数的敏感性研究[J]. 西北工业大学学报, 2000, 18(3): 442-445.

HU C J. On the sensitivity of aircraft longitudinal flying qualities to aerodynamic derivatives at high angle of attack[J]. Journal of Northwestern Polytechnical University, 2000, 18(3): 442-445 (in Chinese).

[11]张曙光, 李雪峰, 孙金标. 横航向飞行品质对参数的灵敏度分析[J]. 飞行力学, 2000, 18(2): 19-22.

ZHANG S G, LI X F, SUN J B. Analysis on sensitivity of lateral and directional flying qualities to variation of parameters[J]. Flight Dynamics, 2000, 18(2): 19-22 (in Chinese).

[12]SALTELLI A, MARIVOET J. Non-parametric statistics in sensitivity analysis for model output: A comparison of selected techniques[J]. Reliability Engineering & System Safety, 1990, 28(2): 229-253.

[13]HELTON J C, DAVIS F J. Survey of sampling-based methods for uncertainty and sensitivity analysis[J]. Reliability Engineering & System Safety, 2006, 91(10-11): 1175-1209.

[14]SOBOL I M. Sensitivity estimates for nonlinear mathematical models[J]. Journal of Mathematical Model, 1993, 1(4): 407-414.

[15]BORGONOVO E. A new uncertainty importance measure[J]. Reliability Engineering & System Safety, 2007, 92(6): 771-784.

[16]PUENTE E F, TARANTOLA S, GHRAYEB S, et al. Application of global sensitivity analysis to nuclear reactor calculations[J]. Procedia-Social and Behavioral Sciences, 2010, 2(6): 7726-7727.

[17]RUAN W B, LU Z Z， WEI P F. Estimation of conditional moment by moving least squares and its application for importance analysis[J]. Proceedings of the Institution of Mechanical Engineers Part O: Journal of Risk and Reliability, 2013, 227(6): 641-650.

[18]阮文斌, 吕震宙, 安军, 等. 不确定条件下复合材料结构的全局灵敏度分析[J]． 复合材料学报, 2014, 31(3): 699-706．

RUAN W B, LYU Z Z, AN J, et al. Global sensitivity analysis for composite structures with uncertainty[J]. Acta Materiae Compositae Sinica, 2014, 31(3): 699-706 (in Chinese).

[19]中 国民用航空规章第25部: 运输类飞机适航标准: CCAR-25-R4[S]. 北京: 中国民用航空局, 2011.

Chinese Civil Aviation regulation Part 25 Airworthiness standards: Transport category airplanes: CCAR-25-R4[S]. Beijing: Civil Aviation Administration of China, 2011 (in Chinese).

[20]吕震宙, 宋述芳, 李洪双, 等. 结构机构可靠性及可靠性灵敏度分析[M]. 北京： 科学出版社, 2009.

LYU Z Z, SONG S F, LI H S, et al. Analysis for reliability and reliability sensitivity of structural system[M]. Beijing: Science Press, 2009 (in Chinese).

[21]YOUNG P. Time variable and state dependent modelling of nonstationary and nonlinear time series[M]//RAO S T. Developments in time series analysis. New York: Springer, 1993: 374-413.

阮文斌男， 硕士， 助理工程师。主要研究方向： 民用飞机飞行载荷设计。

Tel: 021-20865564

E-mail: ruanwenbin@comac.cc

刘洋男， 硕士， 工程师。主要研究方向： 民用飞机飞行载荷设计。

Tel: 021-20865563

E-mail: liuyang6@coamc.cc

熊磊男， 硕士， 工程师。主要研究方向： 民用飞机飞行载荷设计。

Tel: 021-20865559

E-mail: xionglei@comac.cc

Influence of side aerodynamic derivative uncertainty on side flight load based on global sensitivity analysis

RUAN Wenbin*, LIU Yang, XIONG Lei

General Configuration and Aerodynamics Department, Shanghai Aircraft Design and Research Institute,Shanghai201210, China

Considering the uncertainty of aerodynamic derivative used in flight load calculation, combining with the equations of motion for yaw maneuver, the influence of side aerodynamic derivative uncertainty on side flight load is investigated, utilizing the variance-based global sensitivity analysis (GSA) method. According to the parameters of a certain aircraft, the ranking results of GSA are obtained using the proposed method. The results show that: the derivative of side force coefficient with respect to angle of sideslip has the most significant influence on the vertical tail side load due to sideslip and damping, as well as total vertical tail side load, besides the influences of weathercock stability derivative and rudder control effectiveness are also significant; the vertical tail side load due to rudder is only influenced by the derivative of side force coefficient with respect to rudder deflection; tail-off side load is mainly influenced by weathercock stability derivative, rudder control effectiveness and the derivative of tail-off side force coefficient with respect to angle of sideslip; yaw damping derivative has almost no influence on all side loads. Meanwhile, the example verifies the validity of the method, which is of benefit to promoting the calculation precision of flight load in aircraft design.

global sensitivity analysis; uncertainty; aerodynamic derivative; flight load; variance; yaw maneuver

2015-06-29； Revised： 2015-09-04； Accepted： 2015-09-25； Published online： 2015-10-1015:02

. Tel.： 021-20865564E-mail: ruanwenbin@comac.cc

2015-06-29； 退修日期： 2015-09-04； 录用日期： 2015-09-25；

时间： 2015-10-1015:02

www.cnki.net/kcms/detail/11.1929.V.20151010.1502.002.html

.Tel.： 021-20865564E-mail: ruanwenbin@comac.cc

10.7527/S1000-6893.2015.0264

V212.11

A

1000-6893(2016)06-1827-06

引用格式： 阮文斌， 刘洋， 熊磊． 基于全局灵敏度分析的侧向气动导数不确定性对侧向飞行载荷的影响[J]． 航空学报, 2016, 37(6): 1827-1832. RUAN W B, LIU Y, XIONG L. Influence of side aerodynamic derivative uncertainty on side flight load based on global sensitivity analysis[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(6): 1827-1832.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

URL： www.cnki.net/kcms/detail/11.1929.V.20151010.1502.002.html