A Double-Index Method to Classify Kuroshio Intrusion Paths in the Luzon Strait

Zhida HUANG,Hailong LIU,Jianyu HU,and Pengfei LIN

1State Key Laboratory of Marine Environmental Science,College of Ocean and Earth Sciences,Xiamen University,Xiamen 361102

2State Key Laboratory of Numerical Modeling for Atmospheric Sciences and Geophysical Fluid Dynamics, Institute of Atmospheric Physics,Chinese Academy of Sciences,Beijing 100029

A Double-Index Method to Classify Kuroshio Intrusion Paths in the Luzon Strait

Zhida HUANG1,Hailong LIU*2,Jianyu HU1,and Pengfei LIN2

1State Key Laboratory of Marine Environmental Science,College of Ocean and Earth Sciences,Xiamen University,Xiamen 361102

2State Key Laboratory of Numerical Modeling for Atmospheric Sciences and Geophysical Fluid Dynamics, Institute of Atmospheric Physics,Chinese Academy of Sciences,Beijing 100029

A double index(DI),which is made up of two sub-indices,is proposed to describe the spatial patterns of the Kuroshio intrusion and mesoscale eddies west to the Luzon Strait,based on satellite altimeter data.The area-integrated negative and positive geostrophic vorticities are defined as the Kuroshio warm eddy index(KWI)and the Kuroshio cold eddy index(KCI), respectively.Three typical spatial patterns are identified by the DI:the Kuroshio warm eddy path(KWEP),the Kuroshio cold eddy path(KCEP),and the leaking path.The primary features of the DI and three patterns are further investigated and compared with previous indices.The effects of the integrated area and the algorithm of the integration are investigated in detail.In general,the DI can overcome the problem of previously used indices in which the positive and negative geostrophic vorticities cancel each other out.Thus,the proportions of missing and misjudged events are greatly reduced using the DI. The DI,as compared with previously used indices,can better distinguish the paths of the Kuroshio intrusion and can be used for further research.

Luzon Strait,Kuroshio intrusion,mesoscale eddy,double-index method

1.Introduction

The Luzon Strait(LS)is located between Taiwan Island and Luzon Island and is a primary channel for water exchange between the South China Sea(SCS)and the Northwest Pacific(Fig.1).The Kuroshio,a western boundary current in the Northwest Pacific,transports mass,heat and other properties into the SCS through the LS.The warm and salty Kuroshio water significantly affects circulation and stratification in the northern SCS(e.g.,Wyrtki,1961;Metzger and Hurlburt,1996;Lan et al.,2004;Qu et al.,2004;Cai et al., 2005;Tian et al.,2006).Although much work has been performedregardingthe pathwayofthe Kuroshiointrusion(e.g., Qiu et al.,1984;Li and Wu,1989;Li et al.,1998;Caruso et al.,2006;Yuan et al.,2006;Nan et al.,2011a,2014),how the Kuroshiointrudes into the SCS is still debated due to the lack of long-term and systematic in-situ observations.

Early observations suggested that the Kuroshio intrusion varies seasonally,with strong intrusion during winter and weak intrusion during summer(Wyrtki,1961;Lan et al., 2004).Based on the shape of the path,the Kuroshiointrusion has been classified into several types,such as“the Kuroshio SCS branch”(Qiu et al.,1984)and“the Kuroshio loop”(Li and Wu,1989).Hu et al.(2000)summarized four typical types of the Kuroshiointrusionaccordingto previousstudies: the Kuroshio direct branch,the Kuroshio loop,the Kuroshio extension,and the anticyclonic rings.Recently,Caruso et al.(2006)depicted five types of Kuroshio intrusion paths based on satellite altimeter data,including the Kuroshio SCS branch,the Kuroshio loop,the detached anticyclonic eddy, the cyclonic intrusion,and the leaping path.These classifications provide a basic framework for understanding and analyzing the dynamics of the Kuroshio intrusion.

Recently,oceanographers have attempted to identify the paths of the Kuroshio intrusion more objectively and quantitatively(Nan et al.,2011a,2014;Tsui and Wu,2012;Lu and Liu,2013).The Kuroshio SCS index(KSI)was proposed by Nan et al.(2011a)by using the area integral of geostrophic vorticity(GV)west of the LS(19°–23°N,118°–121°E).Using the KSI,these authors distinguished three types of Kuroshio intrusion paths:the looping,leaping,and leaking paths.The occurrence proportion of each path was computed,and the KSI was used to study the seasonal variation of the looping path(Nan et al.,2014)and was applied to ocean model output(Nan et al.,2011a).However,there are several aspects of the KSI that still require improvement. First,the selection of the integral area could be done so more objectively,because the results are sensitive to the chosen area.Second,the positive and negative GVs can cancel eachotherout,whichcanleadtomissingloopingorleapingevents and the misjudgment of some events.

©Institute of Atmospheric Physics/Chinese Academy of Sciences，and Science Press and Springer-Verlag Berlin Heidelberg 2016

Fig.1.Mean dynamic topography(cm)near the LS from 1993 to 2013.The blue dashed line represents the mean dynamic topography values of 115 cm.Box 1(19°–23°N,118°–121°E) and Box 2(20°–22°N,119°–121°E)are chosen to calculate the KSI1 and KSI2.Box 2 is the integral area for the DI.

Due to the large horizontal or vertical shear of the Kuroshio around the LS,a large number of eddies occur in this region.In addition,satellite and in-situ observations show that a warm eddy occurs in the center of the looping path(Li et al.,1998;Yuan et al.,2006;Nan et al.,2011a) and a cold eddy exists west of the leaping path(Tian et al., 2006;Yang et al.,2010;Nan et al.,2011b).The occurrences of these eddies suggest close relationships between the Kuroshio paths and mesoscale eddies in the northeastern SCS.Because themeanflowandthemesoscaleeddiescannot be separated by using the values of GV,the KSI more likely demonstrates the spatial patterns for both the Kuroshio intrusion path and mesoscale eddies,rather than for the Kuroshio intrusion path only.

In the present study,we propose two sub-indices to describe the Kuroshio intrusion and mesoscale eddies,which is referred to as the double index(DI)hereafter.The DI is composed of two sub-indices:the areal integration of the negative GV,called the Kuroshio warm eddy index(KWI);and the areal integration of the positive GV,called the Kuroshio cold eddy index(KCI).The definition of the DI is given in section 2.Section 3 presents the primary characteristics of the DI,which includes the classification of the Kuroshio intrusion paths,the seasonal occurrence proportions of these paths,and the differences between the DI and KSI in terms of the integral area and calculation method.The results are

summarized and discussed in section 4.

2.Data and methods

This study uses the merged satellite altimeter products for the period 1993–2013[spatial resolution:(1/4)°×(1/4)°] provided by AVISO(http://www.aviso.oceanobs.com). Satellite altimeter data were obtained weekly by averaging the daily products(with a mean of±3 days).The absolute dynamic topography(ADT)is the sum of the sea level anomaly(SLA)and mean dynamic topography.The surface geostrophic currents are computed using the ADT and a geostrophicrelation.Because the ADT data in shelf areas are contaminated by tides and internal waves(Yuan et al.,2006; Nan et al.,2011a),the data where the water depth is less than 200 m are excluded.

The KSI proposed by Nan et al.(2011a)is defined and written as Iksas follows:

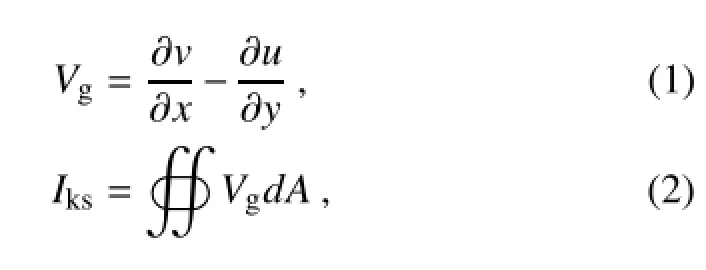
where u and v are the surface geostrophic currents,and A is the integrated area.The GV is written as Vg.To avoid the impacts caused by the offset of positive and negative GVs, we propose two sub-indices:the areal integration of negativeGV,defined as the KWI;and the areal integration of positive GV,defined as the KCI.The KWI and KCI are written as Ikwand Ikc:

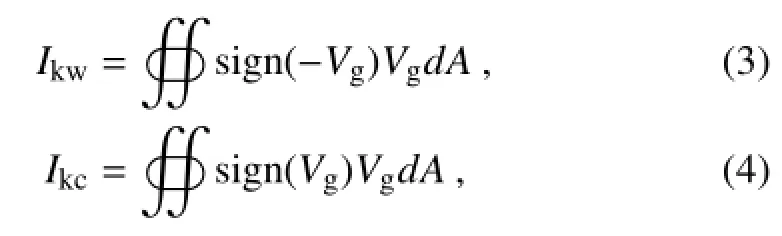
where sign()is the sign function and is defined as follows:

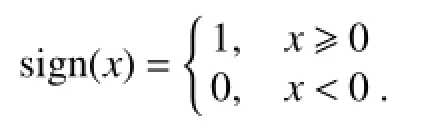
We adjust the integrated region to a smaller area[(20°–22°N,119°–121°E);Box 2 in Fig.1],based on the spatial patternofthe correlationcoefficientbetweentheKSI andGV. At the same time,we also consider the sizes of mesoscale eddies in this region,which are about 150–200 km around this region.It is better that the size of the box should be larger than the sizes of eddies,or at least comparable with the sizes of eddies.So,a 2°×2°box is good for capturing eddies.The integrated area in Nan et al.(2011a)was(19°–23°N,118°–121°E)and is shown as Box 1 in Fig.1.However,the maximumcorrelationcoefficientbetweentheKSIandGV inevery grid is approximately0.2(passing the 99%significance level of the t-test,0.081)in Box 1(not shown),which indicates that the spatial representationof the KSI is poor(the resulting impacts will be shown later).Now,the largest correlation coefficient is approximately 0.5(passing the 99%significance level of the t-test,0.081)for the new area.For convenience, the KSIs calculated in Box 1 and Box 2 are named KSI1 and KSI2,respectively.By definition,KSI2 is the sum of the KWI and KCI.

In addition,we use the standard deviations as thresholds and obtain the following three types of typical Kuroshio intrusion paths:the events smaller than the standard deviation of the KWI are defined as the Kuroshio warm eddy path (KWEP);the events larger than the standard deviation of the KCI are defined as the Kuroshio cold eddy path(KCEP);and the remaining events are defined as the leaking path.

Because the DI is composed of the KWI and KCI,it is possible that the KWEP and KCEP both satisfy the criteria. When this situation occurs,an additional criterion is introduced.The two sub-indices are normalized with their own mean and standard deviation values,respectively.If the absolute value of the normalized deviation of the KWI(KCI)is large,then the event is a KWEP(KCEP).This situation only accounts for 1.5%of the 1095 cases,which suggests that it is appropriateto definetwo sub-indicesto identifythe Kuroshio intrusion paths.

Asshownabove,therearetwomajordistinctionsbetween the DI and KSI.First,the area of integration for the DI is smaller and mainly centered in the northern LS.Second,the DI treats positive and negative GVs separately.The impacts of these differences on the classifications of the Kuroshio intrusion path are shown in the following sections.

3.Results

3.1.DI and its related spatial pattern

Figure 2 shows the time series of the weekly KWI and KCI computed by using the AVISO data from 1993 to 2013. The KWI has significant seasonal variations and its minimum(maximum)values mainly occur in the winter(summer),with values less than-4.0×105m2s-1in the winters of 1995/1996,1996/1997,and 2011/2012.The KCI is characterized by intraseasonal variations.Power spectral analysis also indicates that significant intraseasonal and seasonal signals principally exist for the KWI,but only intraseasonalsignals exist for the KCI(not shown).

Fig.2.Time series of the weekly KWI and KCI(m2s-1)based on the AVISO data from 1993 to 2013.Red and blue dots represent the KWEP and the KCEP,respectively.The pink dashed lines denote μ±σ,where μ and σ are the mean and standard deviation.

The mean(μ)and standard deviation(σ)values of the KWI are-1.50×105and 0.75×105m2s-1,and those of the KCI are 1.93×105and 0.55×105m2s-1,respectively. The pink dashed lines in Fig.2 denote the μ±σ.Based on the classification method mentioned in section 2,the red and blue dots represent KWEP and KCEP events,while the rest represent leaking path events.The occurrence proportions for these three types of paths,KWEP,KCEP and the leaking paths,are 14.1%,14.8%and 71.1%,respectively,which are similar to the results of the KSI in magnitude(Nan et al., 2011a).

Figures 3a–f show the composites of the ADT,the surface geostrophic currents,and the SLA for the three types of paths based on the DI.The corresponding GV composites and eddy kinetic energy(EKE)are shown in Figs.3g–l. When KWEP events occur,the main Kuroshio path enters the SCS in the middle portion of the LS and flows outward in an anticyclonic pattern in the northern part(Figs.3a and g)to form a“Kuroshio loop”(Li and Wu,1989;Xue et al., 2004;Nan et al.,2011a).The center of the Kuroshio loop is located southwest of Taiwan Island and has a minimumnegative GV value(Fig.3g)with SLA and EKE values larger than 15 cm and 0.15 m2s-2(Figs.3b and h).Therefore,a KWEP event is mainly characterized by a warm eddy in the center of the Kuroshio loop.The warm eddy may be detached from the Kuroshio loop,based on in-situ and satellite altimeter observations(Li et al.,1998;Caruso et al.,2006;Yuan et al., 2006).

When a KCEP event occurs,the main Kuroshio path flows across the LS,and a branch of the Kuroshio enters the SCS in the northern part of the LS(Figs.3c and i).Maximum positive GV values exist left of the main Kuroshio path (Fig.3i),with a minimumSLA value of less than-5 cm(Fig. 3d)and a maximumEKE valueof approximately0.09m2s-2(Fig.3j).These results demonstrate that the KCEP is mainly characterized as a cold eddy,which occurs west of the LS, when the main Kuroshio path leaps the LS.A branch of the Kuroshio water enters the SCS in a cyclonic pattern in the northern region of the LS.Parts of this branch may return to the main Kuroshio path(Fig.3c),which corresponds with the cyclonic intrusion presented by Caruso et al.(2006).It is worth noting that there are two warm eddies with maximum SLA values larger than 5 cm on both sides of the cold eddy. One eddy is in the SCS and the other is just outside the LS (Fig.3d).The relationships between the warm and cold eddies in the SCS are consistent with the conceptual model of eddy–Kuroshio interaction during the summer proposed by Nan et al.(2011b).Their results show that a cold eddy often forms when the main Kuroshio path leaps the LS during the summer,which induces the formation of a warm eddy in the SCS and west of the cold eddy.Several studies have revealed that the warm eddy east of the LS will allow the main Kuroshio path to overcome the β effect more easily and leap the LS(Sheremet,2001;Zhao and Luo,2010;Yuan and Wang,2011).

Because the leaking path accounts for more than 70%, the composite ADT and surface geostrophic currents of the leaking path are similar to those of the mean state(Figs.1 and 3e).According to the ADT maps,there is no significant distinction between the leaking path and KCEP because both paths have a branch of Kuroshio flowing into the SCS.The branch of Kuroshio in the KCEP is northward relative to that intheleakingpath.However,thedifferencebetweentheleaking path and KCEP is clear when looking at the SLA maps, in which no eddy is in the leaking path(Fig.3f).For the leaking path,the intensities of negative and positive GVs are relatively weak north and south of the integrated area(Fig. 3k),and the EKE values are smaller than those of the KWEP or KCEP in the SCS(Fig.3l).Therefore,weaker mesoscale eddy activities in the northeastern SCS are the main features of the leaking path.

As shown above,the newly defined DI method can be used to identify three typical Kuroshio intrusion paths:the KWEP,KCEP,and leaking path.These three paths not only focus on the main Kuroshio path,but also on the typical spatial patterns of both the Kuroshio path and mesoscale eddies west of the LS.The ratios between the standard deviations and ensemble mean of each category—KWEP,KCWP and leaping path—have also been computed(not shown).The values are around 10%in the study domain.The small ratio suggests that the patterns of each event in each category are close to each other.

3.2.Kuroshio intrusion paths from the KSI

To compare the DI with the KSI,we calculate two KSIs (KSI1 and KSI2),as discussed in section 2.The integral area and the calculation method of KSI1 are the same as the KSI proposed by Nan et al.(2011a).The calculation method of KSI2 is the same as that of KSI1,but uses the integral area of the DI,which is smaller than that of KSI1(Fig.1).Therefore,the impacts of the integral area can be determined by comparing KSI1 and KSI2,and the impacts of the calculation methods can be evaluated by comparing KSI2 with the DI.In the present sub-section,we present the primary features of KSI1 and KSI2,including the indices themselves, the occurrence proportions of different paths,and the spatial patterns of composited flows and eddies.

Figures 4a and b show the time series of the weekly KSI1 and KSI2 from 1993 to 2013.Overall,KSI1 is consistent withtheKSI calculatedbyNanetal.(2011a),with onlysmall differences resulting from different dataset versions.Nevertheless,large differences occur between KSI2 and KSI1 (Figs.4a and b),and KSI2 is similar to KWI(Fig.2).Figures 4a and b also indicate that KSI1 has a significant intraseasonal signal,while KSI2 has both intraseasonal and seasonal signals.

Using the standard deviations as thresholds,the red and blue points represent the looping and leaping path events and the remaining points represent the leaking path events. The occurrence proportions of the three patterns are approximately 15%,15%and 70%for the looping,leaping and leaking paths,respectively(Table 1),which are close to those of the DI shown above.

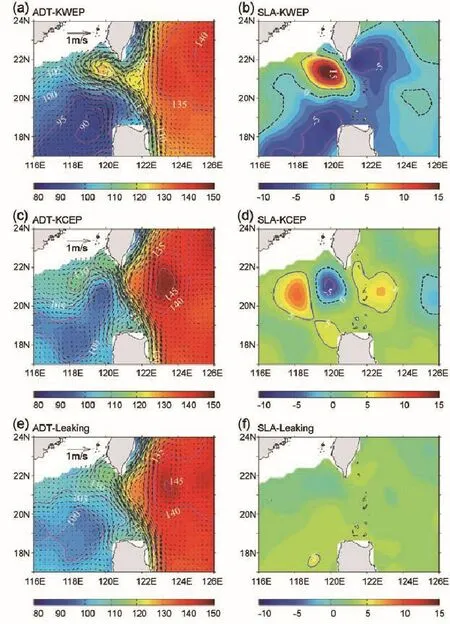
Fig.3.Composite ADT(cm)and corresponding surface geostrophic currents(m s-1)for the(a)KWEP,(c)KCEP,and(e) leaking path,according to the DI method shown in Fig.2.Panels(b,d,f)are the corresponding SLAs(cm);(g,i,k)are the corresponding GVs(s-1)and surface geostrophic currents(m s-1);(h,j,l)are the corresponding EKE(m2s-2).The thick dashed lines are the ADT values of 115 cm in(a,c,e).The thin dashed lines denote the 0 SLA contours in(b,d,f).The purple lines denote the 0 GV contours in(g,i,k).

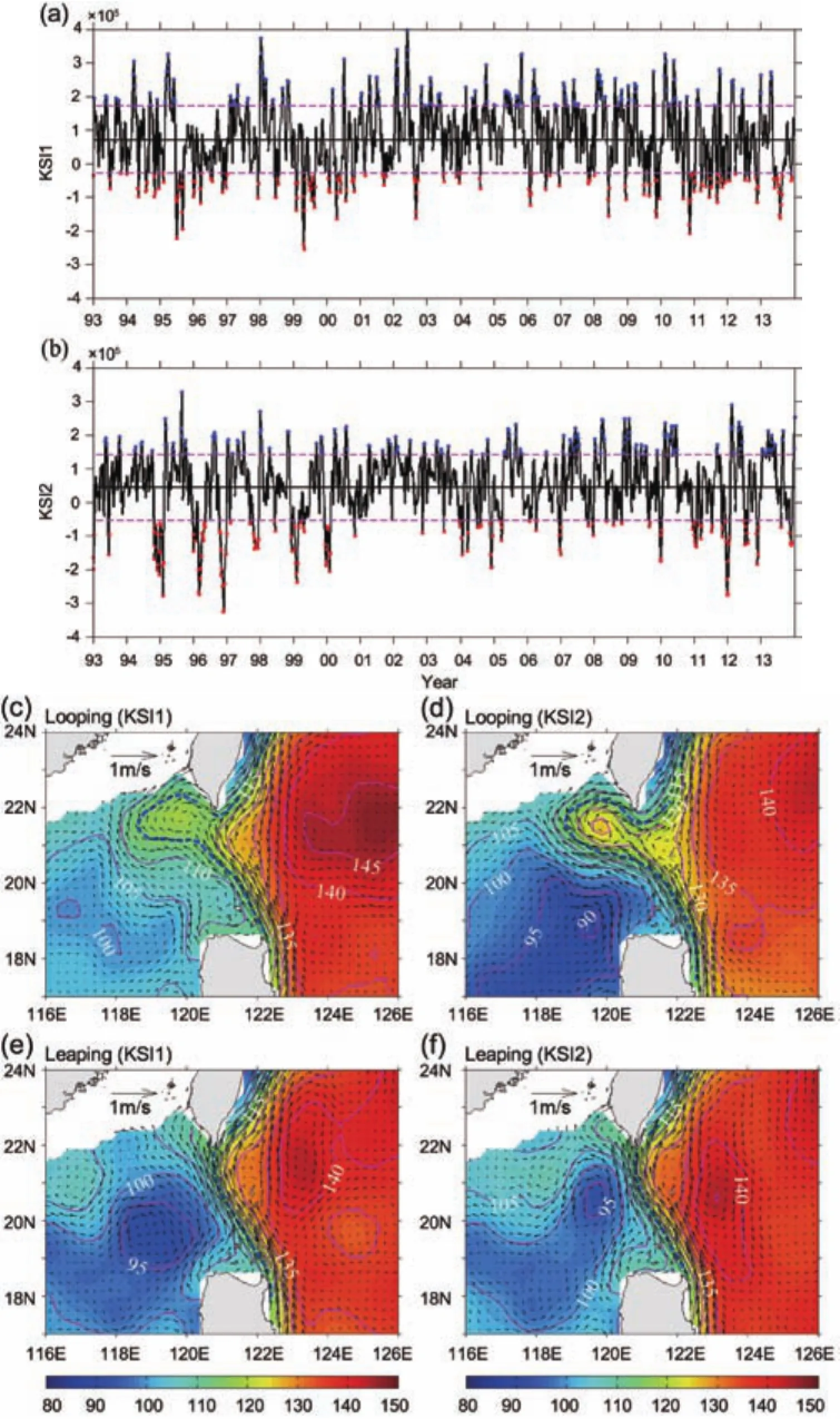
Fig.4.Time series of the weekly(a)KSI1 and(b)KSI2(m2s-1)based on the AVISO data from 1993 to 2013.Red and blue dots represent the Kuroshio looping path and Kuroshio leaping path,respectively.The pink dashed lines denote μ±σ,where μ and σ are the mean and standard deviation.Panels(c,e)are the composite ADT(cm)and corresponding surface geostrophic currents(m s-1)for the Kuroshio looping path and the Kuroshio leaping path according to the KSI1.Panels(d,f)are similar to (a,c)except for the KSI2.The thick dashed lines in(c–f)are the ADT values of 115 cm.

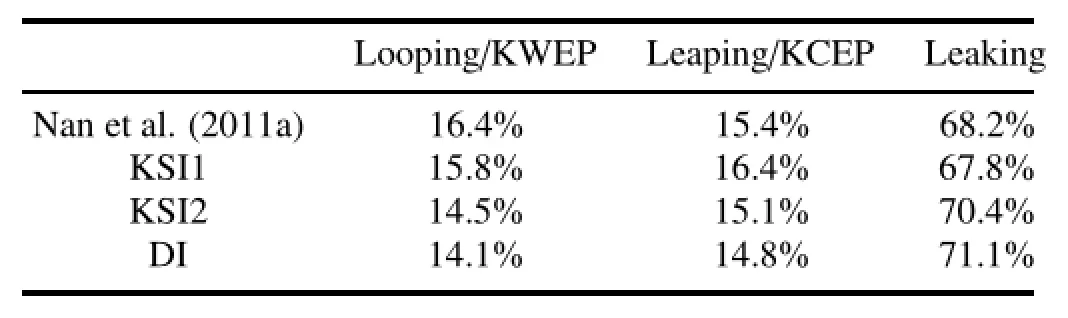
Table 1.List of probabilities for the three types of Kuroshio intrusion paths.

Figures 4c and e show the composite of the ADT and the corresponding surface geostrophic currents for the looping and leaping paths for KSI1.Figures 4d and f are the same as Figs.4c and e,respectively,but for KSI2.Because the patterns of the leaking paths are similar to those in Fig.3e, the figures are not shown here.The distributions of the ADT and the surface geostrophic currents for the looping path and leaping path identified by KSI1(Figs.4c and e)are consistent with the results of Nan et al.(2011a),but different from the paths identified by KSI2.The greatest distinction between KSI2 and KSI1 is that the ADT value in the center of the looping path identified by KSI2 is approximately 10 cm larger than that identified by KSI1(Figs.4c and d), which suggests that the events for the looping path classified by KSI2 are stronger than those classified by KSI1.For the leaping path,a cold eddy exists west of the LS,which is identified by KSI2 and is smaller than the Luzon cold eddy northwestofLuzonIsland identifiedbyKSI1(Figs.4e andf).

According to a preliminary comparison between KSI1 and KSI2,the integral area will significantly affect events and flow features;however,the occurrenceproportionsof the threepatterns forKSI1 andKSI2 are close.These results also indicate that the paths of Kuroshio intrusion are more sensitive to changes in the integral area.

3.3.Comparison of the DI with the KSI

3.3.1.Monthly proportions of the looping/KWEP and leaping/KCEP paths

The Kuroshio intrusion has seasonal signals that are strong in winter and weak in summer(e.g.,Wyrtki,1961). Thus,investigatingtheseasonalvariationsofthethreeindices can highlight the distinctions among them.Figure 5 shows the monthly proportions of the looping/KWEP and leaping/ KCEP paths identified by the three indices.Hereafter,for simplicity,we simply refer to the looping and leaping paths. Overall,the values of the proportions show that the differences between KSI1 and KSI2 are much larger than those between KSI2 and DI,especially for the looping path.

For the looping path,both KSI2 and the DI indicate that the maximum proportion occurs during winter,with approximately 40%in December and 30%in November,and that theminimumproportion(less than10%)appearsduringsummer.Comparedwith KSI2(ortheDI),theproportionofKSI1 has semi-annualvariations,with two peaks exceeding20%in both July and November.These peaks suggest that the seasonal variations of the looping path identified by KSI1 are not consistent with observations(e.g.,Wyrtki,1961;Lan et al.,2004).

The seasonal proportion of the leaping path is generally higherin the winterand lowerin the summerfor KSI1,which obviouslyconflictswithobservations(e.g.,Wyrtki,1961;Qu, 2000;Lan et al.,2004).The differences between KSI1 and KSI2 for the leaping path occur mainly in February and August,with KSI1 yielding a 20%higher(10%lower)result than KSI2 in February(August).The differences(over 5%) between KSI2 and the DI for the leaping path occur in April, May,June,July and October,with the largest occurring(over 10%)in April.This indicates that the consistency of KSI2 and the DI for the leaping path is less than that for the looping path.

According to the seasonal proportion of the looping and leaping paths,KSI2 and the DI appear closer to the observations than KSI1.These results indicate that the indices are sensitive to the integral area.Furthermore,the major differences between KSI2 and the DI are the proportions of the leaping path in spring and summer.The following analysis will focuson what causes these differencesand also on which index is more reasonable.

3.3.2.Impacts of the integral area

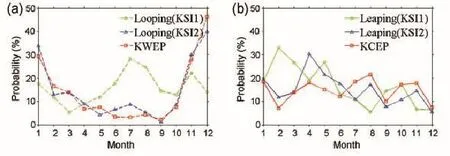
Fig.5.(a)Monthly variation of the proportions for the looping/KWEP path identified by KSI1,KSI2 and the DI.Panel (b)is similar to(a)except for the leaping/KCEP path.

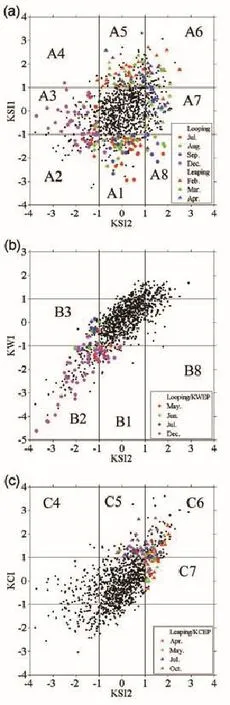
Fig.6.Scatter diagrams for the normalized(a)KSI2–KSI1,(b) KSI2–KWI and(c)KSI2–KCI.The colored dots(triangles) highlight the cases for the looping/KWEP(leaping/KCEP)path in particular months according to significant differences in the monthly proportion,as shown in Fig.5.The black dots in the center area are the cases for the leaking path identified by the two indices.

Figure 6 presents the scatter diagrams for the normalized KSI2–KSI1,KSI2–KWI,and KSI2–KCI.According to the definition,the looping(leaping)events are identified by values smaller(greater)than-1(+1),and the leaking path events are the black dots in the center area identified by the two indices.In Fig.6a,the events in the A2 and A6 zones are identified as the looping and leaping paths,respectively,by both KSI1 and KSI2;events in the A1 and A5 zones are identified as leaking paths by KSI2 and as looping and leaping paths by KSI1;and events in the A3 and A5 zones are identified as the looping and leaping paths by KSI2 and as leaking paths by KSI1.The largest difference occurs in the A4 and A8 zones.Events in the A4 zone are identified as the leaping path by KSI1,as the looping path by KSI2,and vice versa in the A8 zone.Figures 6b and c are similar to Fig.6a,but for KSI2–KWI and KSI2–KCI.The key zones for looping paths are B1,B2,B3 and B8,and those for leaping paths are C4, C5,C6 and C7.

Based on the significant differences between the monthly variations of the proportions for Kuroshio intrusion types (Fig.5),we use colored dots and triangles to highlight the looping and leaping events that occur during particular months(Fig.6).When comparing KSI1 with KSI2,we choose July,August,September and December for the looping path,and February,March and April for the leaping path (Fig.6a).Additionally,to compare KSI2 and the DI,May, June and December are selected for the looping paths(Fig. 6b),and April,May,July and October are selected for the leaping paths(Fig.6c).The analysis of the following compositeandsinglecasemapsaccordingtoscatterdiagramswill demonstrate the causes of the differences in the monthly occurrence proportions shown in Fig.5.

First,we analyze the impacts of the integral area based on the scatter diagram of KSI1–KSI2(Fig.6a).To determine the main differences between KSI1 and KSI2,we focus on the A1,A2,A5 and A7 zones.Figure 7a presents the composite ADT and corresponding surface geostrophic currents according to the 21 cases in July in the A1 zone(red dots in Fig.6a;Table 2).These cases are the looping paths for KSI1 and leaking paths for KSI2.The classification for KSI2 is obviously more reasonable.Figure 7b is the same as Fig.7a,but for 26 cases in the A3 zone in December(purple dots in Fig.6a;Table 2)that are identified as leaking paths by KSI1 and looping paths by KSI2.The composite ADT and current pattern are obviously a looping path and not a leaking path,which also indicates that KSI2 is more reasonable.

For the situation shown in Fig.7a,no evident positive or negative GV center occurs in the integration area.A weak negative GV center in the northern part of Box 1 causes the integrationtobe morenegativeandis mistakenlyclassified as the looping path by KSI1.According to Fig.7b,although a strong negative GV center occurs in the northern part of Box 1,the positive GV center in the south will cancel out the negative value.Thus,there is no peak for KSI1.These results can also explain the causes of the relatively high(low)occurrence proportion of the looping path in July(December)by KSI1.

Figure 7c shows the composite ADT and surface geostrophic currents of 19 events in the A5 zone in February(red triangles in Fig.6a;Table 2),and Fig.7d is similar toFig.7c,except for 20 events in the A7 zone in April(blue trianglesinFig.6a;Table2).InFig.7c,theeventsareidentified as the leaping path by KSI1 and as the leaking path by KSI2; however,the opposite situation is shown in Fig.7d.For the leaping path,a strong cold eddy with larger positive GV exists west of the LS,based on both KSI1 and KSI2.However, the center of the cold eddy identified by KSI1 is more southwestward than that of KSI2.The strong cold eddy cannot prevent the Kuroshio from entering into the SCS completely, because a branch of the Kuroshio extends into the SCS in the leaping path,which is identified by KSI1 and KSI2(Figs. 4e and f).Moreover,the intrusion branch of the Kuroshio for the leaping path appears stronger than that for the leaking path.Therefore,it is difficult to determine which index is more reasonablefor the leaping path.In addition,this finding suggeststhatitis impropertocallthispaththe“leapingpath”. The ADT distribution in Fig.7c is closer to that in Figs.3e and 4e,while the ADT distribution in Fig.7d is similar to that in Figs.3c and 4f.Therefore,we infer that KSI2 better depicts the spatial pattern of mesoscale eddies and mean flow.

Figure 8 is similar to that of Fig.7,except for the A4 and A8 zones,which have relatively fewer events(only 4 events in the A4 zone and12 eventsin the A8 zone).These also suggest that both KSI1 and KSI2 are reasonable to some extent. Figure 8a is the same as Fig.7d,except for 4 events in April and 4 events in September in the A8 zone(green and blue dots in Fig.6a;Table 2).A cold eddy is located just west of the main Kuroshio path,and a warm eddy is located just west of the cold eddy.Because the entire area integration of GV is negative,the paths are classified as looping paths for KSI1.However,it is clear that this path is not a looping path. Figure 8b shows the same situation,but with only one case on 31 August 2011 when compared with the composite map shown in Fig.8a.

Because only 4 cases occur in the A4 zone,a single case map is shown here instead of a composite one.Figures 8c–f present the distributions of the ADT for the 4 cases,which are identified as leaping paths by KSI1 and looping paths by KSI2.Although the flow pattern details vary,the main features clearly indicate loopingpaths in Figs.8c,d and f,which indicate that KSI2 is more reasonable than KSI1.The situation shown in Fig.8e is special.Although a negative GV occurs in the north part of the area,the value is small.Based on its definition,this path should not be classified as a leaping or looping path.Thus,both KSI1 and KSI2 misjudged this case.

The causes of missed or misjudged events when comparing KSI1 and KSI2 are shown above.Furthermore,we confirm that indices are sensitive to the integral area,and KSI2 calculated in a relatively small region seems more reasonable.The integral area for KSI1 is larger than the circulation structure and mesoscale eddy scales.Thus,the offset of positive and negative GVs possibly results in the reduction of the absolute value of the integrated GV for the looping path (e.g.,Fig.7a)and the criterion for the leaping path(e.g.,Fig. 7c).However,KSI2 also results in misjudgment,as shown in Fig.8e.

3.3.3.Impacts of calculation methods

A comparison of the Kuroshio intrusion paths between KSI2 and the DI will further reflect the difference caused bythealgorithmoftheindices,whichconsiderswhethertocomputethe positiveandnegativeGVs separately.Figures6b and c present scatter diagramsfor the normalizedKSI2–KWI and KSI2–KCI.From the distribution of the scatter dots,the consistency between KSI2 and KWI is better than that between KSI2 and KCI,which can also be seen in Fig.5.Similar to the analysis of the impacts of the integral area,we also apply the composite method to investigate the causes of the differences between KSI2 and the DI.

Table 2.List of date information for events in Figs.7,8 and 9.

Fig.7.Composite ADT(cm)and corresponding surface geostrophic currents(m s-1)for(a)21 red dots in July in zone A1,(b)26 purple dots in December in zone A3,(c)19 red triangles in February in zone A5,and(d)20 blue triangles in April in zone A7.The zones A1,A3,A5 and A7 are shown in Fig.6.The black line represents the 120.5°E section across the LS.The red boxes are Box 1(19°–23°N,118°–121°E)and Box 2(20°–22°N,119°–121°E).

Figure 9a shows the composite ADT and surface geostrophiccurrentsof 11 events in the B1 zone in December (purple dots in Fig.6b;Table 2).Figure 9b is similar to Fig. 9a,except for 7 events in the B3 zone in July(blue dots in Fig.6b;Table 2).The former is identified as a leaking path by KSI2 and as the KWEP by the DI,while the latter is classified as a looping path by KSI2 and as the KCEP by the DI. These two situations reflect the main problems of KSI2.In Fig.9a,it is clear that the judgment of the DI is correct.The misjudgment of KSI2 occurs because of the offset of the positive and negativeGVs south and north of the integrated area. Although no strong negative GV center is shown in Fig.9b, most of the integrated area is covered by relatively weak and negative GV.Therefore,the absolute values of the integrated GV of these cases are much more evident when using KSI2 than in the real looping path in which the large positive and negative values are offset.Thus,the misjudgment of KSI2 occurs.

Fig.8.As shown in Fig.7 except for(a)four green dots in August and four blue dots in September in zone A8(shown in Fig.6a).Panel(b)is one case for(a)on 31 August 2011.The ADT and corresponding surface geostrophic currents on(c)20 January 1993,(d)7 December 1994,(e)12 February 1997 and(f)22 October 2008 identified as the leaping path by KSI1 and looping path by KSI2,as shown in zone A4.The red boxes are Box 1(19°–23°N,118°–121°E)and Box 2(20°–22°N,119°–121°E).

Fig.9.As in Fig.7 except for(a)11 purple dots in December in zone B1,(b)7 blue dots in July in zone B3,(c)10 blue triangles in July in zone C5,and(d)17 red triangles in April in zone C7.Zones B1,B3,C5 and C7 are shown in Fig.6.

Figures 9c and d are similar to Fig.9a,except for 10 events in the C5 zone in July(blue triangles in Fig.6c;Table 2)and 17 events in the C7 zone in April(red triangles in Fig. 6c;Table 2).The former is classified as the leaking path by KSI2 and as the KCEP by the DI,and the latter situation is classified as the leaping path by KSI2 and as the leaking path by the DI.As shown in Figs.9c and d,it is difficult to determine which index is better.For the cases shown in Fig.9c, two cores of positive and negative GVs are located in the integrated area west of the LS.For KSI2,the offset of positive and negative GVs results in a leaking path.However,for the DI,the positive GV is stronger than the negative GV.Thus, a KCEP occurs according to the DI.For the cases in Fig.9d, weak positive GV anomalies occur throughout the study region.Because the absolute value of the positive GV is larger than that of negative GV for KSI2,the path is classified as a leaping path.The KCIs of these cases are smaller than those with strong cold eddies for the DI,and these cases are classified as leaking paths.In addition,the cases shown in Figs. 9c and d occur in July and April,respectively.The above two examples can also explain the differences in the occurrence proportion of the leaping path between KSI2 and the DI in Fig.5b.

Figure 10 shows the ADT and surface geostrophic currents for the three events in the C4 and B8 zones.It is interesting that both the KWI and KCI values satisfy the criterion (Fig.2).In Figs.10a and b,two centers are shown in this study area:one has a large positive GV,and the other has a negative GV.The two events described above are both identified as looping paths by KSI2 because the absolute value of the negative GV in the north is larger than that of the positive GV in the south.For the DI,the KWEP and KCEP criteria are both satisfied.As mentioned in section 2,when this situation occurs,we classify the path based on the normalized deviations of the KWI and KCI from their mean values.That is,when the normalized deviation of KWI is larger than that of KCI,we define this as a KWEP case,and vice versa.The case in Fig.10c is similar to the above two cases,except that the positive GV value in the south is relatively large.Therefore,the flow type is identified as the leaping path by KSI2. For the DI,the case is identified as a KCEP case because the KCI has a larger deviation from the mean value than the KWI.The above three cases indicate that the DI can address the special cases well whenthe KWI andKCI bothsatisfy the criteria.

Generally,the separated positive and negative GVs in the DI overcome the shortcomings of KSI2 and result in a large reduction in the probability of the error.The DI can further highlight the anticyclonic pattern of the main Kuroshio path entering the SCS,while the positive and negative GVs are cancelled out in KSI2.

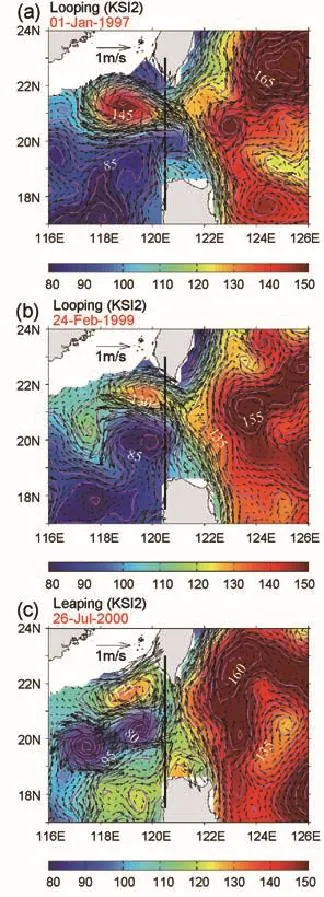
Fig.10.The ADT(cm)and corresponding surface geostrophic currents(m s-1)on(a)1 January 1997,(b)24 February 1999 and(c)26 July 2000.Panels(a,b)are the two dots in zone C4 and are identified as the looping path according to KSI2.Panel (c)is the only dot in zone B8 and is classified as the leaping path by KSI2.Zones C4 and B8 are shown in Fig.6.The black line represents the 120.5°E section across the LS.

4.Summary and discussion

This paper proposes two sub-indices to describe the spatial patterns of the mean flow and mesoscale eddies west of the LS based on the KSI put forward by Nan et al.(2011a). The area-integrated negative GV is defined as the KWI,and the area-integrated positive GV is defined as the KCI.These two sub-indices are collectively referred to as the DI.

By applying the DI to the satellite altimeter data for the period 1993–2013,three typical spatial patterns are identified:the KWEP,the KCEP,and the leaking path.The main features of these three types of patterns can be summarized as follows:(1)For the KWEP,the main Kuroshio path enters the SCS in the middle and outflows in the northernpart of the LS in an anticyclonic pattern with a warm eddy southwest of Taiwan Island(Figs.3a and b).(2)For the KCEP,the main Kuroshio path leaps the LS with a cold eddy to the west of the LS(Figs.3c and d)and a Kuroshio branch flows cyclonically into the SCS following the north edge of the eddy.(3) For the leaking path,a Kuroshio branch enters the SCS in the central LS and no eddies occur west of the LS(Figs.3e and f).Therefore,the classifications of the DI not only focus on the typical path of the Kuroshio intrusion but also on the typical spatial distributionsof the Kuroshiointrusion path and the mesoscale eddies in the northeast of the SCS.Thus, the names of the two sub-indices of the DI and their corresponding spatial patterns are referred to as KWI/KWEP and KCI/KCEP.

In addition,the occurrence proportions of the KWEP, KCEP and leaking paths are computed,yielding results of 14.1%,14.8%and 71.1%,respectively.The KWEP has significant seasonal variation,with a maximum proportion of approximately 31%in the winter and a minimum proportion of approximately 3%in the summer.The occurrence proportions of the KCEP range between 11%and 17%with no evident seasonal variability.However,the value in the summer is relatively large.In addition,both the KWEP and KCEP have clear intraseasonal and interannual signals.

Thisstudyprimarilyfocusesontheimpactsoftheintegral areaandthecalculationmethodstoclassifythespatialpattern of the Kuroshio intrusion and the mesoscale eddies,which correspond to the differences between the DI and KSI.These results reveal that these indices are sensitive to the integral area.The typical spatial pattern of flow and its intensity can be changed by using different integrated areas.Furthermore, the events and the seasonal variability of the occurrence proportion of the typical flow are different.If a relatively large integral region is selected,the positive and negative GVs offset each other.Therefore,some events of the looping or leaping paths will be missed,especially during the winter for the looping path.Furthermore,it is possible that some events are identified as having a typical pattern by mistake.This misjudgment frequently occurs in July for the looping path and in February for the leaping path.

The old computation method will also result in missing or misjudging the looping path.The former is due to the offset of the large values of positive and negative GVs,and thelatter to the relatively large integrated values of GVs from a regionfullofweaknegativeGVs withnocancellationbypositive GVs.However,the main difference between the DI and KSI2 occurs when classifying the leaping path or the KCEP, especially in the spring and summer seasons.In the spring, the weak positive GV is not cancelled out and is identified as a leaping path by KSI2 and a leaking path by the DI.During the summer,the large positive GV is cancelled out and identified as a leaking path by KSI2 and a KCEP by the DI.

Generally,the DI improves upon the KSI,in which cancellation between positive and negative GVs occurs.The proportions of missed and misjudged events are greatly reduced when applying the DI.The problem of the DI caused by the two sub-indices is also solved by introducing an additional criterion.However,two problems still remain for the DI.First,the GV cannot identify the contributions from the mean flows or the mesoscale eddies.Second,the features of the DI are not comprehensivelypresented in this paper.Work is underway to address the variability of the DI and the relationship between the DI and the volume transport,as well as evaluate its typical patterns.

Acknowledgements.This work was supported by the National Basic Research Program of China(Grant Nos.2015CB954004 and 2013CB956204)and the National Natural Science Foundation of China(Grant Nos.41276006,U1405233 and 41023002).The ADT and SLA data were distributed by AVISO(ftp://ftp.aviso.oceanobs. com).We appreciate the AVISO center for the online data,and the two anonymous reviewers for their helpful comments.

REFERENCES

Cai,S.Q.,H.L.Liu,W.Li,and X.M.Long,2005:Application of LICOM to the numerical study of the water exchange between the South China Sea and its adjacent oceans.Acta Oceanologica Sinica,24,10–19.

Caruso,M.J.,G.G.Gawarkiewicz,and R.C.Beardsley,2006: Interannual variability of the Kuroshio intrusion in the South China Sea.Journal of Oceanography,62,559–575.

Hu,J.Y.,H.Kawamura,H.S.Hong,and Y.Q.Qi,2000:A review on the currents in the South China Sea:Seasonal circulation, South China Sea Warm Current and Kuroshio intrusion.Journal of Oceanography,56,607–624.

Lan,J.,X.,W.Bao,and G.P.Gao,2004:Optimal estimation of zonal velocity and transport through Luzon Strait using variational data assimilation technique.Chinese Journal of Oceanology and Limnology,22,335–339.

Li,L.,and B.Y.Wu,1989:A Kuroshio loop in South China Sea?—On circulations of the northeastern South China Sea.Journal of Oceanography in Taiwan Strait,8,89–95.(in Chinese)

Li,L.,W.D.Nowlin Jr.,and J.L.Su,1998:Anticyclonic rings from the Kuroshio in the South China Sea.Deep Sea Research Part I:Oceanographic Research Papers,45,1469–1482,doi: 10.1016/S0967-0637(98)00026-0.

Lu,J.Y.,and Q.Y.Liu,2013:Gap-leaping Kuroshio and blocking westward-propagating Rossby wave and eddy in the Luzon Strait.J.Geophys.Res.,118,1170–1181,doi:10.1002/jgrc. 20116.

Metzger,E.J.,and H.E.Hurlburt,1996:Coupled dynamics of the South China Sea,the Sulu Sea,and the Pacific Ocean.J. Geophys.Res.,101,12 331–12 352.

Nan,F.,H.J.Xue,F.Chai,L.Shi,M.C.Shi,and P.F.Guo, 2011a:Identification of different types of Kuroshio intrusion into the South China Sea.Ocean Dynamics,61,1291–1304, doi:10.1007/s10236-011-0426-3.

Nan,F.,H.J.Xue,P.Xiu,F.Chai,M.C.Shi,and P.F.Guo, 2011b:Oceanic eddy formation and propagation southwest of Taiwan.J.Geophys.Res.,116,C12045,doi:10.1029/2011JC 007386.

Nan,F.,H.J.Xue,and F.Yu,2014:Kuroshio intrusion into the South China Sea:A review.Progress in Oceanography,137, 314–333,doi:10.1016/j.pocean.2014.05.012.

Qiu,D.Z.,T.H.Yang,and Z.X.Guo,1984:A west-flowing current in the northern part of the South China Sea in summer. Journal of Tropical Oceanography,3,65–73.(in Chinese)

Qu,T.D.,2000:Upper-layer circulation in the South China Sea. J.Phys.Oceanogr.,30,1450–1460.

Qu,T.D.,Y.Y.Kim,M.Yaremchuk,T.Tozuka,A.Ishida,and T.Yamagata,2004:Can Luzon Strait transport play a role in conveying the impact of ENSO to the South China Sea?J. Climate,17,3644–3657.

Sheremet,V.A.,2001:Hysteresis of a western boundary current leaping across a gap.J.Phys.Oceanogr.,31,1247–1259.

Tian,J.W.,Q.X.Yang,X.F.Liang,L.L.Xie,D.X.Hu,F. Wang,and T.D.Qu,2006:Observation of Luzon Strait transport.Geophys.Res.Lett.,33,L19607,doi:10.1029/2006GL 026272.

Tsui,I.-F.,and C.-R.Wu,2012:Variability analysis of Kuroshio intrusion through Luzon Strait using growing hierarchical self-organizing map.Ocean Dynamics,62,1187–1194,doi: 10.1007/s10236-012-0558-0.

Wyrtki,K.,1961:Physical oceanography of the Southeast Asian waters.Naga Report,Volume 2.The University of California, Scripps Institution of Oceanography,1–195.

Xue,H.J.,F.Chai,N.Pettigrew,D.Y.Xu,M.C.Shi,and J.P.Xu,2004:Kuroshio intrusion and the circulation in the South China Sea.J.Geophys.Res.,109,C02017,doi: 10.1029/2002JC001724.

Yang,Q.X.,J.W.Tian,and W.Zhao,2010:Observation of Luzon Strait transport in summer 2007.Deep Sea Research Part I: Oceanographic Research Papers,57,670–676,doi:10.1016/ j.dsr.2010.02.004.

Yuan,D.L.,W.Q.Han,and D.X.Hu,2006:Surface Kuroshio path in the Luzon Strait area derived from satellite remote sensing data.J.Geophys.Res.,111,C11007,doi:10.1029/ 2005JC003412.

Yuan,D.L.,and Z.Wang,2011:Hysteresis and dynamics of a western boundary current flowing by a gap forced by impingement of mesoscale eddies.J.Phys.Oceanogr.,41,878–888,doi:10.1175/2010JPO4489.1.

Zhao,J.,and D.-H.Luo,2010:Response of the Kuroshio current to eddies in the Luzon Strait.Atmos.Oceanic Sci.Lett.,3, 160–164.

Huang,Z.D.,H.L.Liu,J.Y.Hu,and P.F.Lin,2016:A double-index method to classify Kuroshio intrusion paths in the Luzon Strait.Adv.Atmos.Sci.,33(6),715–729,

10.1007/s00376-015-5171-y.

17 July 2015;revised 29 October 2015;accepted 30 November 2015)

Hailong LIU

Email:lhl@lasg.iap.ac.cn