扩散和沉降耦合作用下霾气溶胶分布的研究

方爱平 田蓬勃 应 钺 蔡佳音 苟明岳 郭启隆 宋 倩 杨宇驰 喻有理 王小力

（西安交通大学理学院，陕西西安 710049）

扩散和沉降耦合作用下霾气溶胶分布的研究

方爱平 田蓬勃 应 钺 蔡佳音 苟明岳 郭启隆 宋 倩 杨宇驰 喻有理 王小力

（西安交通大学理学院，陕西西安 710049）

通过气溶胶的特性，从扩散、沉降、凝聚三个方面对霾微粒进行分析.发现对于霾微粒，沉降速度采用孤粒子沉降速度是完全可行的；凝聚作用对一般的霾分散系作用很小以至于可以忽略.在这一前提下，采用对流扩散方程描述扩散和沉降的耦合作用，并给出了积分形式的解析解.参考高斯烟羽模型，给出一种较为典型的初值条件，并在污染物接触地面完全反射的假设下通过数值方法模拟未来的污染物浓度演化.模拟结果显示:（1）在无风的条件下，霾消散的速度是相当缓慢的；（2）霾的演化中起最主要作用的是沉降.

扩散；沉降；凝聚；扩散系数；Stokes速度；高斯烟羽模型

近年来，能源消耗量增大，燃烧化石燃料的过程中排放到空气中的化学物质以及颗粒状的污染物（如尘、煤等）不断增加，造成了各种形式的大气污染.其中，霾这一现象尤其引人关注.霾，也称阴霾、灰霾，是指大量烟、尘等微粒悬浮而形成的浑浊现象.霾的核心物质是空气中悬浮的灰尘颗粒，气象学上称为气溶胶颗粒.霾中含有数百种大气化学颗粒物质，可引起多种疾病.此外，霾影响大气能见度，常引发交通事故.为了治理霾，在实际工作中，需要根据污染源的位置、高度、气象情况等条件正确推算出污染物在大气中的浓度.再以此来制定合理的治理措施.

本文从气溶胶的通性［1］入手分析影响雾霾分散系的因素.考虑扩散、沉降、凝聚以及周围环境的影响，通过分析论证了采用对流扩散方程描述霾分布演化的可行性.以高斯正态烟羽模式为背景，研究单一污染源排放出的污染物，推算出了周围地区的污染物浓度分布随时间的演化，以供后续使用.

1 模型建立

我们基于两个基本假设:（1）考察的空间足够大以至于可以认为是无界的；（2）环境中无风且温度均匀，通过气溶胶的通性，给出描述扩散，沉降，凝聚的方程.并通过分析合理的简化模型.

1.1 控制气溶胶运动的方程

1）扩散

扩散是物质分子从高浓度区域向低浓度区域转移，直到均匀分布的现象.由菲克定律，扩散的速率与物质的浓度梯度成正比.故在流场v内，有对流扩散方程［2］

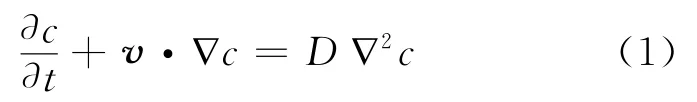
其中，c为质量浓度；D为扩散系数，可以由下式确定［2，3］

其中，kB为玻尔兹曼常数；T为绝对温度；μ为动力黏度系数，在空气中μ=1.81×10-5Pa·s；dp为粒子粒度；Cu为库宁汉滑移修正系数，常温常压下，施特劳斯给出的库宁汉修正系数为［3］

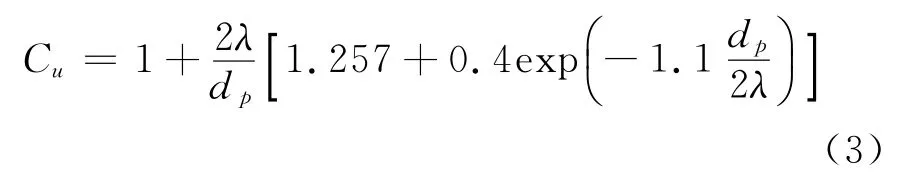
其中λ为平均自由程［2］，有

其中λ0为标准状态下的空气分子平均自由程，λ0= 0.0665μm.

2）沉降

在外力作用下，气溶胶粒子与气流之间产生相对运动，产生阻力.假定粒子所受阻力服从斯托克斯定律，则随着粒子和气流的速度差的增大，阻力也随之增大.若力场是均匀的，则粒子必有一个最终沉降速度.在重力场中，孤立粒子的最终沉降速度即Stokes速度为［3］

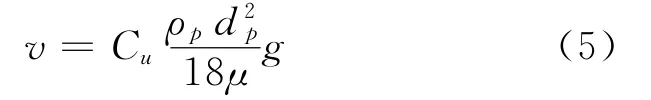
其中ρp为胶粒的质量密度.实际情况中，分散系内的气溶胶粒子会互相影响，实际的沉降速度与Stokes速度会有一定差异.在单分散体系的假设下，有沉降速度公式［3］为

其中，ϕ为分散系中粒子的体积浓度；S为沉降系数，此处S=-6.55.

3）凝聚

先考虑简单单分散热凝聚或Smoluchowski凝聚:它假设粒子是单分散性的；粒子一旦接触就互相黏附；这些粒子生长得很慢.在这些假设下推导出气溶胶数量浓度的变化率［3］为

中位数粒度［3］为

当粒度为正态分布时，由Lee和Chen提出的计算公式可以得到平均凝聚系数［3］

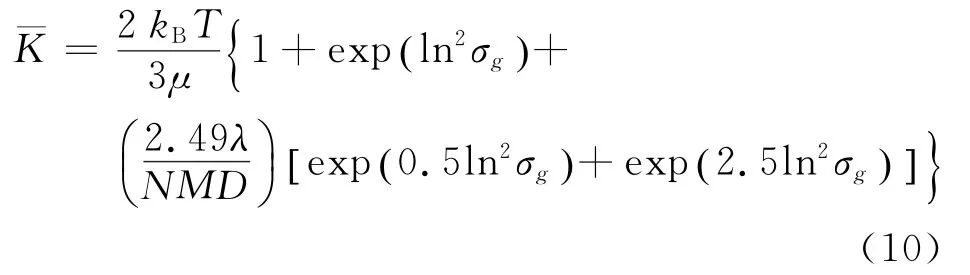
其中，NMD为计数中位直径；σg为几何标准偏差，它被定义为

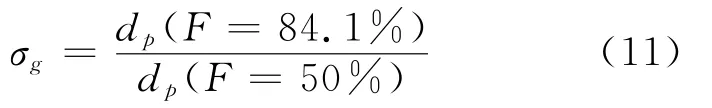
当粒度分布符合正态分布时

由于这些粒子生长得很慢，在考虑的时间范围内，σg的变化不计，则粒子数为

中位数粒度

1.2 简化模型

对模型中的影响因素进行适度的分析，排除一些影响很小的项，以简化模型，降低求解的难度.

1）忽略凝聚的影响

考虑粒度为正态分布时的凝聚情况，考察一个如图1所示的具有代表性的实例，通过估算凝聚速度说明凝聚的效果在我们考虑的时间尺度下可以忽略.

图1 北京西北城区夏季大气PM10的粒度分布［4］

仅考虑烟尘集合体，注意到它的频率分布呈现单峰分布，用正态分布对其进行拟合，通过参数估计可以得到NMD=0.295μm；σg=1.86.

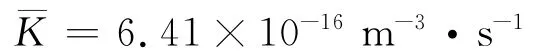
在标准状态，由Lee和Chen给出了公式（10）的平均凝聚系数［3］为要求得气溶胶的数量密度，胶粒的线度应该用质量中位径MMD，有NMD和MND的换算关系估算［3］

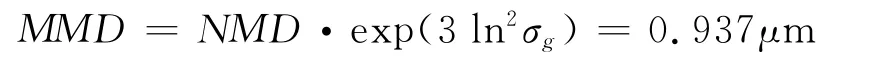
考虑PM10值为300μg·m-3时的情形，通过计算此时N0≈1.5×107m-3，考察粒子数随时间变化的方程

将粒子数变为初值的1/2所用的时间称为半衰期T，则由以上讨论可以得到

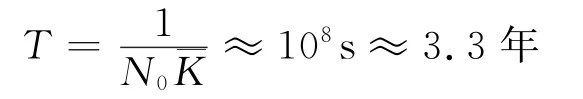
注意到沉降速度大约为10-5m·s-1，如果污染源离地地面的距离为101m量级，则污染源处霾粒子沉降到地面的时间约为106s，可见在此情形下凝聚的时间尺度远远大于我们考虑的时间范围，故在以下的讨论中不考虑凝聚的作用.

2）忽略多粒子互相作用对沉降的影响

考虑多粒子相互作用时的沉降公式:

1.3 模型建立

通过以上的分析，霾分散系的演化可以归结为扩散和Stokes沉降的耦合作用.沉降的效果可以等效于对流扩散方程中的对流项.由于考虑的是无风环境，控制霾随时间演化的方程如下表示:

其中v为沉降速度.

2 模型求解

考虑前面分析过的例子，假设环境处于标准状态，PM10值为300μg·m-3.代入一个基于高斯烟羽模型的较具有代表性的初值条件，求解霾分散系的演化情况.

2.1 参数的确定

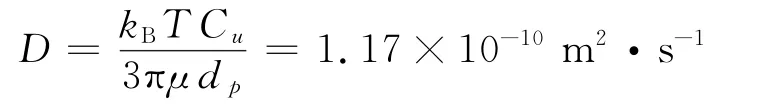
由中位数粒度和求解假设可以确定扩散系数为同样可以由公式确定沉降的Stokes速度为

2.2 无源空间对流扩散方程的解析解

为了简化问题，假设考虑上方为无界空间，地面按一定比例吸收运动到地面上的污染物，假设我们已经得到无界边界条件下的浓度场u，那么“反射”的效果即z＜0的u场“翻转”到z＞0的空间中并乘上一个比例系数，再与z＞0处的u场叠加，就可以得到有地面边界条件下的浓度场c控制u的方程如下为

运用格林函数，先考虑在r=0处一小团气体的质量为m0的气体的扩散情况，在球坐标下

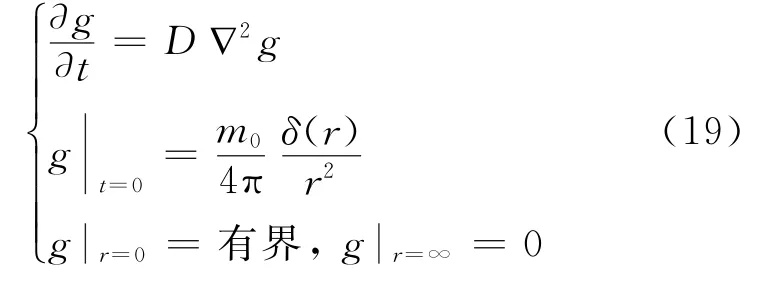
解得

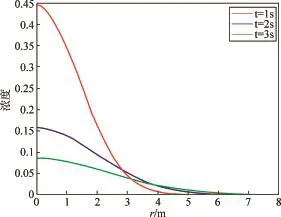
图2 时间t取1，2，3s时的浓度分布示意图

加入对流项，相当于坐标系在以v的速度向-z方向平移，只需在解中加入一个坐标变换

或

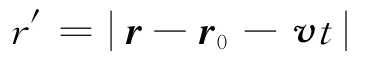
则仍有

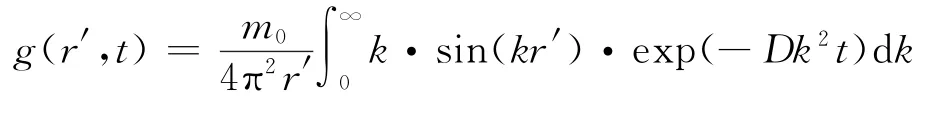
将由高斯烟云模型得到的初值条件看作delta函数的叠加，则整块烟云的浓度场应该是一小团气体扩散产生的浓度场g的叠加.

其中d V为r0附近的一个面积微元.

设地面的反射率为k，则由之前提供的计算方法

其中r=（x，y，z），z＞0.

代入初值条件和之前求得的系数，可以得到任意时刻的浓度分布.

2.3 初值条件的确立

对于连续均匀排放的点源，源强为Q（mg·s-1），离地面的有效排放高度为he（m）.令平均风速u（m·s-1）沿x轴方向.当风速较大，稳定之后，可以假设在y、z方向上浓度C呈正态分布，则扩散公式［2，3］为

式中:

C—下风向任意位置（x，y，z）的污染浓度，mg·m-3；

σy—扩散系数，y方向的标准差，m；

σz—扩散系数，z方向的标准差，m；

Q—排放源强，mg·s-1；

U—排放口高度处的平均风速，m·s-1；

he—有效排放高度.

考虑无风的情形，烟云有向上的初速度，忽略反射项，则可以将高斯烟云模型改写为如下形式

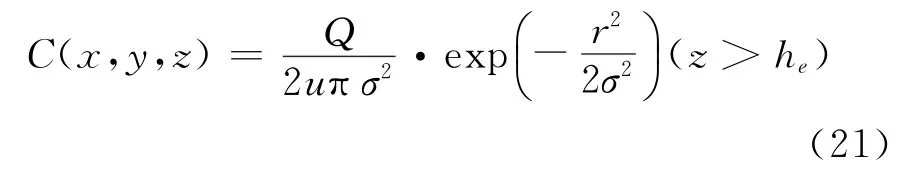
其中:r2=x2+y2，σ为r方向的标准差.

这是一个比较具有代表性的情形，若将它作为初值条件，则它的物理意义为由一点源以较大的初速度向上排放污染物至稳定.之后停止排放，将此处的浓度分布作为初值条件.

为了求解的方便，对初值条件做如下规定:

（1）为了避免在场源处出现奇点，在z＞he的空间中，对分布

（2）为了让浓度场在空间内连续，在z＜he的空间中，假设

（3）为了计算方便，u取1m·s-1，Q取2πmg·s-1，he取10m.

由此得到初值条件的示意图图3所示.

我们将这种形式的的烟云分布作为讨论问题的初值条件.这只是一个值得参考的有一定参考意义的情形，事实上2.2中的讨论可以处理各种形式的初值条件.

图3 基于高斯烟羽模型的初值条件

2.4 数值模拟

代入初值条件和之前求得的系数，可以得到任意时刻的浓度分布，代入系数D=1.17× 10-10m2·s-1，v=1.23×10-5m·s-1，当反射率k=1，t取6，9，12，24天，浓度分布如图4所示.

可见，在无风的环境下，气溶胶污染物的变化是很缓慢的.此外，我们发现在我们考察的情景下，扩散的效果相较于沉降也非常小.这是因为霾气溶胶的粒度较大，沉降速度大，扩散系数小.霾的演化中起主要作用的是沉降作用.

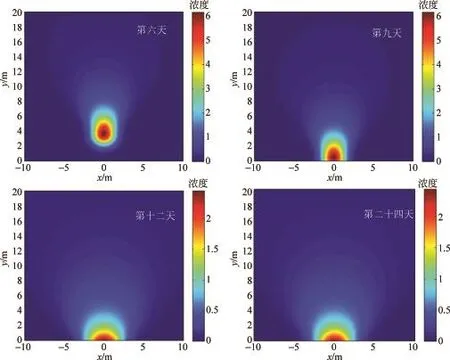
图4 当反射率k=1，第6，9，12，24天的浓度分布示意图

3 结语

本文通过分析，略去了凝聚对粒度的影响和多粒子相互作用对沉降速度的影响，合理地简化了模型.在考虑沉降和扩散的耦合作用时，将沉降的效果用对流等效起来，取得了较好的效果.并通过叠加的方法求出了对流项恒定条件下对流扩散方程的解析解.找到一种典型的烟云分布，通过数值方法解出其演化情况.

但是这一模型也有许多局限.它需要温度恒定，无风或者至少风速恒定这样很强的假设.该模型对污染物的沉积和化学转化过程只做了十分粗略的处理，如果在此方面需要考虑时，模式的应用受到限制.

［1］张小曳.中国大气气溶胶及其气候效应的研究［J］.地球科学进展，2007，22（1）:12-16.

［2］向晓东.气溶胶科学技术基础［M］.北京:中国环境科学出版社，2012.

［3］平措.大气污染扩散长期模型的应用研究［D］.硕士学位论文.天津:天津大学环境科学与工程学院，2006.

［4］邵龙义，时宗波.北京西北城区与清洁对照点夏季大气PM10的微观特征及粒度分布［J］.环境科学，2003，24（5）: 11-16.

STUDY ON THE DISTRIBUTION OF AEROSOL HAZE UNDER THE COUPLED ACTION OF DIFFUSION AND SUBSIDENCE

Fang Aiping Tian Pengbo Ying Yue Cai Jiayin Gou Mingyue Guo Qilong Song Qian Yang Yuchi Yu Youli Wang Xiaoli
（School of Science，Xi’an Jiaotong University，Xi’an，Shaanxi 710049）

In this paper，according to the characteristics of the aerosol，diffusion，subsidence and coagulation these three aspects of haze particles were analyzed.We found that for haze particles，the use of solitary particle sedimentation velocity is feasible；cohesive effect on the general haze dispersion effect is so small that can be ignored.In this context，the use of coupling diffusion and convection-diffusion equation describes the settlement，and the analytic solution of the integral form.Reference Gaussian plume model to give a more typical initial conditions，and under the assumption that the ground can completely reflected the pollutant，the future evolution of the pollutants can be solved by numerical methods.The simulation results show that:（1）in the windless conditions，haze dissipated speed is very slow；（2）The sedimentation plays the most important role in haze evolution.

diffusion；subsidence；cohesion；diffusion coefficient；Stokes speed；Gaussian plume model

2016-05-01

方爱平，女，西安交通大学理学院讲师，博士，主要从事量子光学和大学物理的教学与研究工作.

田蓬勃，男，副教授，主要从事大学物理和热学教学科研工作，研究方向为光学.pbtian@163.com

方爱平，田蓬勃，应钺，等.扩散和沉降耦合作用下霾气溶胶分布的研究［J］.物理与工程，2016，26（4）:104-108.