使用正态分布函数修正推荐系统相关相似性

宋 平，邵 清

(上海理工大学 光电信息与计算机工程学院，上海 200093)



使用正态分布函数修正推荐系统相关相似性

宋 平，邵 清

(上海理工大学 光电信息与计算机工程学院，上海 200093)

为提高协同过滤推荐系统寻找最近邻居集合的准确程度，在传统的相关相似性基础上，提出了一种利用正态分布函数作为修正函数的相关相似性计算方法，该方法依据双方共同评分的项目进行用户相似性评价，利用正态分布函数来修正用户之间评分项目数差距对相关相似性计算产生的负面影响，能够较好地体现用户的相似程度。实验结果表明，在相同条件下，该方法与传统的相关相似性计算方法，在一定程度上提高了寻找最近邻居用户集合的准确度。

推荐系统；相似性；正态分布；修正函数；邻居用户集合

SONG Ping, SHAO Qing

(School of Optical-Electrical and Computer Engineering, University of Shanghai for Science and Technology,Shanghai 200093, China)

为了让用户从大量信息中找到自己感兴趣的信息，推荐系统[1]已逐渐成为电子商务中一个必不可少的工具，并且得到研究者的关注。协同过滤推荐系统[2]是目前为止成功、且运用最多的推荐技术，与传统的直接分析内容进行推荐不同，基于用户的协同过滤推荐系统通过分析用户兴趣，在用户群中找到与指定用户的相似用户，综合户对该项目的喜好程度[3]。为找这些相似用户对同一项目的评价，预测出该用到目标用户的最近邻居进行推荐, 必须度量用户之间的相似性，然后选择相似性最高的若干用户，作为目标用户的最近邻居[4]。目标用户的最近邻居查询是否准确, 直接关系到整个推荐系统的推荐质量, 而要想准确查询目标用户, 需要准确计算不同用户之间的相似性, 所以如何准确计算用户之间相似性就成为提高推荐准确率的关键。计算用户之间相似性的方法主要包括余弦相似性，修正的余弦相似性以及相关相似性等[5]，本文主要在相关相似性的基础上，对基于用户的协同过滤推荐系统中的相关相似性进行改善，设计了一种基于正态分布函数作为修正函数计算用户之间相似性的方法，使得生成相似邻居用户集合更加准确，从而可以提高评分预测的准确程度。

1 相关工作

1.1 推荐算法的基本流程

图1 推荐算法基本流程图

(1)根据系统中用户项的评分建立用户项目评分矩阵；(2)进行用户间相似度的计算，常用的相似性计算有3种；(3)根据计算得到的相似度大小为目标用户选择邻居；(4)预测目标用户对未知项目评分，为其提供推荐列表。

1.2 相似性计算方法

1.2.1 相关参数

为方便阅读和理解，本文中出现的符号和其意义都在表1中呈现，具体如下。

表1 参数列表

1.2.2 相似性度量方法

协同过滤推荐技术中一个必不可少的步骤是计算目标用户与其他用户之间的相似性，从而生成最近邻居集合，进而产生推荐，传统的相似性计算方法有以下3种[6-7]：

(1)余弦相似性。用向量和分别表示用户i和用户j的评分向量，而它们的相似性就是通过计算向量之间夹角的余弦来进行度量，则用户x和用户y之间的相似性为

(1)

(2)修正余弦相似性。 考虑到用户之间评分尺度的不同，公式中利用用户的平均评分作出了一定的修正，即用户i和用户j之间的相似性

(2)

(3)相关相似性。用户之间的相似性通过计算两个用户评分向量之间的线性关系来进行衡量，则用户x和用户y之间的相似性

(3)

余弦相似性度量方法把用户评分看作一个向量，用向量的余弦夹角来度量用户间的相似性，然而没有包含用户评分的统计特征；修正的余弦相似性方法在余弦相似性的基础上，减去了用户对项目的平均评分，该方法更多地体现了用户间的相关性而非相似性；相关相似性方法依据双方共同评分的项目进行用户相似性评价，能够更好地体现用户的相似程度，但相关相似性在计算用户之间相似性上还存在着一些问题。

1.3 相关相似性缺点

下面通过具体事例说明相关相似性存在的问题[8]。

表2 测试数据

(1) 未考虑用户评分项的数量对相似度的影响。

表2中，行与列的交叉点表示用户(1～5)对项目(1～3)的一些评分值。直观来看，User1和User5用3个共同的评分项，并且给出的评分趋势相同，User1与User4只有2个相同评分项，虽然他们的趋势也相似，但由于User4对Item2的评分未知，可能是User4对Item2未发生行为，或者对Item2很讨厌，所以更希望User1和User5更相似，但结果是User1与User4有着更高的结果。 可以看出相关相似性只会对共同评价过的记录进行计算[9]。

同样的场景在现实生活中也经常发生，例如用户A和用户B各观看了200部电影，用户C只看了2部电影，而用户A和B共同观看的200部电影完全相同，虽然不一定给出相同或完全相近的评分，但只要他们之间的趋势相似也应该比另一位用户C只观看了2部相同电影的相似度高。但事实并非如此，如果对这两部电影，两个用户给出的相似度相同或很相近，通过相关相关性计算出的相似度会明显大于观看了相同的200部电影的用户之间的相似度；

(2)只有一个共同评分项则无法计算相关性。由公式可以看出，若两用户之间只有一个共同的评分记录或无共同评分记录，那么将导致分母为0，从这一点也可以看出，相关相似性不适用于冷启动问题。但是，这一特性也有它的好处，当无法计算相关相似性可以认为这两个用户之间没有任何相关性，即他们之间的相似性为零[10]。

2 相似性计算方法

2.1 正态分布函数

正态分布是一个在数学、物理及工程等领域都非常重要的概率分布函数

(4)

通过式(4)可以看出，当x=μ时f(x)达到最大值，而当|x-μ|的值越大，f(x)的值越小。

2.2 修正函数

本文将在正态分布函数的基础上，设用户x的评分项目个数为m，用户y的评分项目个数为n，max(m，n)表示用户x和用户y评分项目集合中评分项目个数较大的项目数，令正态分布函数中μ=0,x=m-n,σ=max(m，n)，经过变换得到函数

(5)

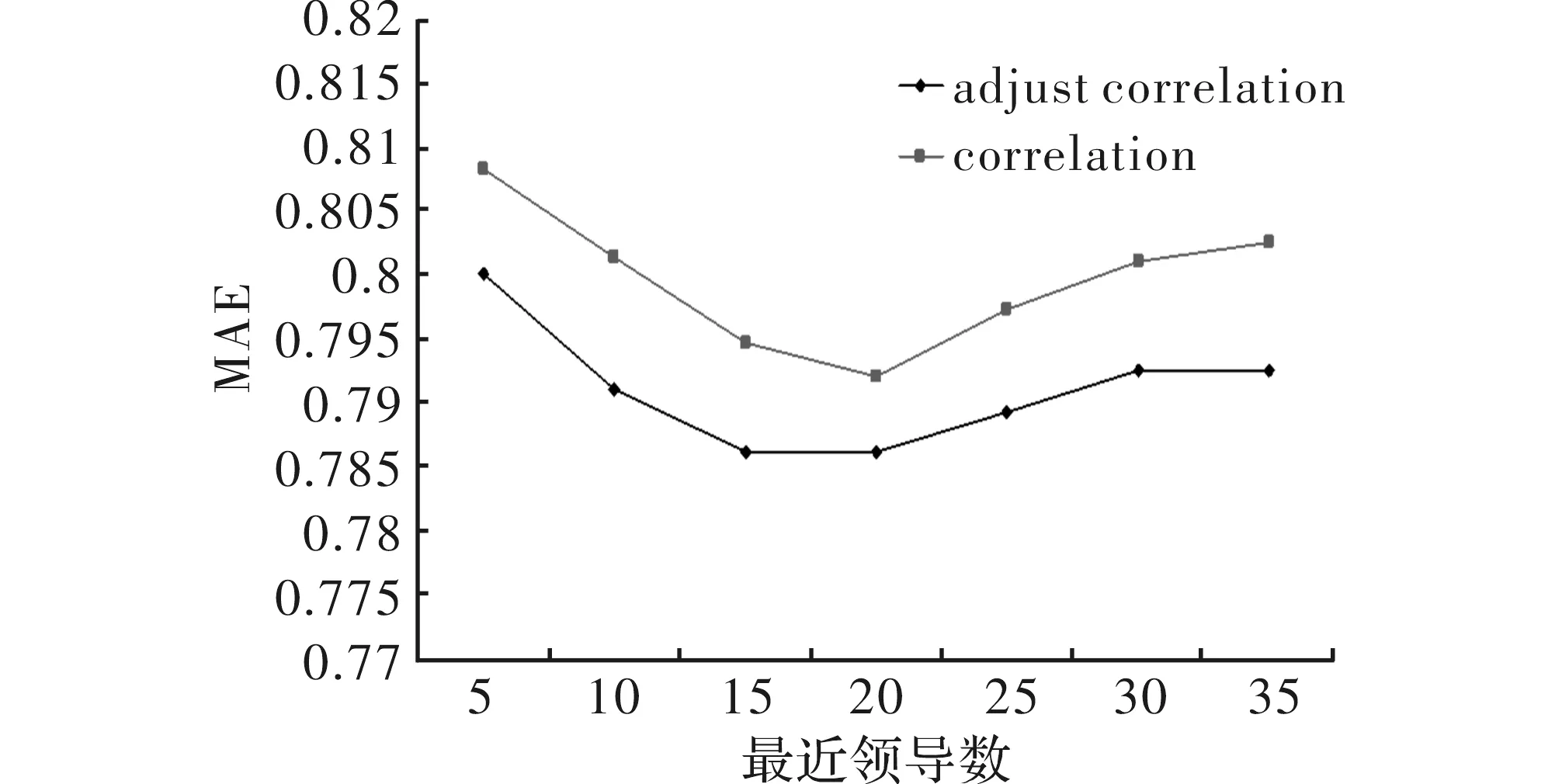
易知，当m=n时，f(m-n)取得最大值为1，当|m-n|越大，f(m-n)的值越小，随着|m-n|不断增加，f(m-n)逐渐从1趋近于0，且0

2.3 改进后的相似性计算方法

正是由于相关相似性没有考虑用户评分记录项的数量对相似度的影响,而导致了两用户A和C观看了相同2部电影的相似度会明显大于观看了相同200部电影的用户A和B之间的相似度。 故可以在相关相似性的基础上添加一个修正函数来修正两用户之间由评分项目数量差距带来的负面影响[11]，即

sim′(x,y)=sim(x,y)f(m-n)

(6)

在前面例子的基础上，由于用户A和用户B有过的评分电影完全相同，则用户A和用户B之间的修正函数为：f(0)=1；而用户A和用户C有过的评分电影只有两部，且二者观看电影数量差距较大，则用户A和用户C之间的修正函数为f(198)=0.376。

假设有5个用户User1～User5，且他们的评分项目数为200，100，70，30和10，则他们之间的惩罚函数值如表3所示。

表3 用户之间的惩罚函数值

表3中行与列的交叉点为两用户的修正函数数值，易知：当两用户的评分项目数差距越大时，修正函数对其相关相似性的修正力度也就越大，这正好符合文中的预期。

3 仿真实验分析

实验将通过在数据集中利用相关相似性和修正的相关相似性分别求出目标用户与其他用户之间的相似度，并按相似度大小生成一个最近邻居用户集合，然后根据邻居集合预测目标用户对该项目的评分。

3.1 实验条件

为了验证提出修正的相关相似性计算方法的一般性和有效性，将分别在MovieLens、Flixster和Epinions这3个数据集上进行实验，他们的评分为1～5，具体用户数、项目数、评分记录如表4所示。

表4 评分数据集

3.2 推荐集的生成

选取与目标用户相似性大小在前N个用户作为用户u的最近邻居集合U按照相似性由大到小排列，根据目标用户u的最近邻居集合U中用户对u的未评分项i的评分，预测u对i的可能的评分值Pu,i，可通过式(6)计算[12]

然后按照Pu,i的大小取前N个项目作为推荐项目推荐给目标用户完成推荐。

3.3 度量标准

实验采用平均绝对误差(MAE)作为实验的评价指标进行实验 ，其公式为

式中，ri是用户u对物品i的实际评分，而Pri是推荐算法给出的预测评分；N为测试集合中的所有记录数目。

3.4 实验结果及分析

为检验本文所提方法的有效性和普遍性，文中基于传统相关相似性(Correlation)和修正后的相关相似性(Adjust Correlation)，在上述3个数据集的基础上，通过实验生成一个相似度由大到小的最近邻居用户集合，并根据邻居集合预测目标用户对该项目的评分，求出评分预测的MAE[13]，实验结果如图2～图4所示。

通过对比可以看出，修正后的相关相似预测评分的MAE比传统相关相似性求出的略低，在最近邻居数逐渐增加到20的过程中，MAE逐渐减小，而最近邻居数>20时，MAE又开始逐渐增加，说明此时会有一些相似度较低的用户“被迫”选入邻居集合，使得算法的精度有所下降，但总体上修正后的相关相似性的评分预测MAE要优于传统的相关相似性。

图2 基于Movielens数据集的MAE

图3 基于Flixster数据集的MAE

图4 基于Epinions数据集的MAE

以上实验结果表明：在数据集MovieLens、Flixster、Epinions上，利用改进后的相关相似性计算方法形成的邻居用户集合。求出的目标用户对项目的预测评分的MAE总体上优于传统的相关相似性计算方法。

4 结束语

针对协同过滤推荐系统中相关相似性的计算方法进行改善，在传统相似性计算方法的基础上提出了一种使用正态分布函数作为惩罚函数来改进相关相似性的计算方法[14]，实验表明，该方法能够有效提高了寻找最近邻居的准确度，从而提高评分预测的准确度。但是当目标用户评分极度稀疏时[15]，该方法的准确度会有所下降，下一阶段将在确保最近邻居集合准确度的基础上，考虑与其他相似性计算方法相结合，尽可能地提高在用户评分极度稀疏的情况下，寻找最近邻居集合的准确程度。

[1] 王国霞,刘贺平.个性化推荐系统综述[J]. 计算机工程与应用,2012,48(7):66-74.

[2] 夏培勇.个性化推荐技术中的协同过滤算法研究[D].青岛:中国海洋大学,2011.

[3] 李聪,梁昌勇,马丽.基于领域最近邻的协同过滤推荐算法[J].计算机研究与发展,2008,45(9):1532-1538.

[4] 冷亚军,梁昌勇,陆青.基于近邻评分填补的协同过滤推荐算法[J].计算机工程,2012,38(21):56-59

[5] Chedrawy Z,Abidi S S R.An adaptive personalized recommendation strategy featuring context sensitive content adaptation[C]. Sydney:Proceedings of Adaptive Hypermedia and Adaptive Web-based Systems,2006.

[6] 马宏伟,张光卫,李鹏. 协同过滤推荐算法综述[J].小型微型计算机,2009(7):1283-1286.

[7] Sarwar B,Konstan J,Borchers A.Using filtering agents to improve prediction quality in the groupLens research collaborative filtering system[M].New York: ACM Press,1998.

[8] Xie F,Xu M,Chen Z. RBRA: A simple and efficient rating-based recommender algorithm to cope with sparsity in recommender systems[J]. IEEE Computer Society,2012,10(1109): 306-311.

[9] Feng Xie, Zhen Chen, Shang Jiaxing. Grey forecast model for accurate recommendation in presence of data sparsity and correlation[J].Knowledge-Based Systems,2014,69(2):179-190.

[10] Jesus Bobadilla, Fernando Ortega, Antonio Hernando,et al. A collaborative filtering approach to mitigate the new user cold start problem[J].Knowledge-Based Systems,2012(26):225-238.

[11] Sang Min Choi, Sang Ki Ko, Yo Sub Han. A movie recommendation algorithm based on genre correlations[J]. Expert Systems with Applications,2012(7): 8079-8085.

[12] 张锋,常会友.使用BP 神经网络缓解协同过滤推荐算法的稀疏性问题[J].计算机研究与发展,2006,43(4): 667-672.

[13] Bobadilla J, Ortega F,Hernando A, et al. A collaborative filtering approach to mitigate the new user cold-start problem[J]. Knowledge-Based Systems, 2012(3): 225-238.

[14] 李聪.电子商务推荐系统中协同过滤瓶颈问题研究[D]. 合肥:合肥工业大学,2009.

[15] Guo Guibing,Zhang Jie, Daniel Thalmann. Merging trust in collaborative filtering to alleviate data sparsity and cold start[J]. Knowledge-Based Systems,2014,57(2):57-68.

Correction of the Correlation Similarity in Recommendation Systems Using the Normal Distribution Function

A calculation method of correlation similarity with normal distribution function as a correction function is proposed based on the traditional correlation for better accuracy of seeking the nearest neighbor set in the collaborative filtering recommendation system. The normal distribution function is employed to correct the negative effect because of the number of items between users on similarity calculation, which well reflects the degree of similarity of users. The experimental results show that the proposed method offer better accuracy of searching for the nearest neighbor set than the traditional method of correlation similarity under the same conditions.

recommender system; similarity; normal distribution; correction function; neighbor user set

2016- 01- 03

国家自然科学基金资助项目(61170277);上海市教委科研创新基金资助项目(02120557)

宋平 (1990-)，男，硕士研究生。研究方向：网络智能。邵清 (1970-)，女，博士，副教授。研究方向：网络智能。

10.16180/j.cnki.issn1007-7820.2016.10.017

TP301.6

A

1007-7820(2016)10-058-04