CMOS反相器和传输门的教学实践

唐普英，姜书艳（电子科技大学 .光电信息学院；.自动化工程学院，成都 610054）

CMOS反相器和传输门的教学实践

唐普英a，姜书艳b
（电子科技大学 a.光电信息学院；b.自动化工程学院，成都 610054）

CMOS反相器和传输门是数字逻辑设计及应用课程中最基本的逻辑门电路，也是学生最先接触到的数字电路，对它们的正确认识是学习其他逻辑门电路的基础。从NMOS反相器存在的问题，到CMOS反相器和传输门的构成，在教学中采用启发式和讨论式教学方法，逐步引导学生如何分析和探究问题的解决过程。学生提高了学习课程的兴趣，把握了知识的来龙去脉，掌握了相关知识的相互关系。

数字电路；反相器；传输门；启发式教学

数字逻辑设计及应用课程是信息技术类专业所共有的一门重要基础课程，同时也是一门重要的工程技术课程，是研究数字系统硬件设计的基础课程。它以大学物理、电路分析基础和模拟电路基础课程为基础，同时又是后续的微机原理、电子设计自动化等课程的基础，在课程教学体系结构中起着承前启后的作用。

CMOS反相器和传输门是数字逻辑设计及应用课程中最基本的逻辑门电路，也是学生最先接触到的数字电路，对它的正确认识是学习其它逻辑门电路的基础。

《教育部关于全面提高高等教育质量的若干意见》的第五条就明确要求“创新教育教学方法，倡导启发式、探究式、讨论式、参与式教学”。提高课堂教学质量是提高教育质量的关键［1］，而教学方法的创新是提高课堂教学质量的一种重要方法。

以CMOS反相器和传输门为例，从NMOS反相器存在的问题出发，运用启发式和讨论式教学方法，逐步引导学生探究CMOS反相器和传输门的构成过程，取得了良好效果。

下面的分析过程中，假设NMOS管和pMOS管均是增强型，并且均工作在开关状态。定义VCC（电源）表示逻辑电平1，地（0 V）表示逻辑电平0。

1 NMOS反相器

图1为NMOS反相器的电路图［2-3］，由一个NMOS管和一个电阻R构成。首先引导学生分析其工作原理，当输入A=1时，NMOS管导通，输出F=0；当输入A=0时，NMOS管截止，输出F=1。该电路具有反相功能，但进一步分析，发现下述问题。

1）当输入A=0时，NMOS管截止，漏极d和源极s之间的电阻很大，输出端F通过上拉电阻R到电源VCC获得高电平，为了得到理想的高电平，电阻R上的压降应尽量小，此时要求电阻R较小。

2）当输入A=1时，NMOS管导通，漏极d和源极s之间的电阻很小，输出端通过导通的NMOS管到地获得低电平，为了降低电路的功耗，此时要求电阻R较大。因此，输入A=1和A=0时，电路输出端F对电阻R的要求是完全不一样的。然而对于一个具体的NMOS反相器电路来说，电阻R的值是相对固定的，与上述要求是矛盾的。

设问:有什么方法能解决上述问题？能否找到一个可随输入电压变化而变化的电阻？

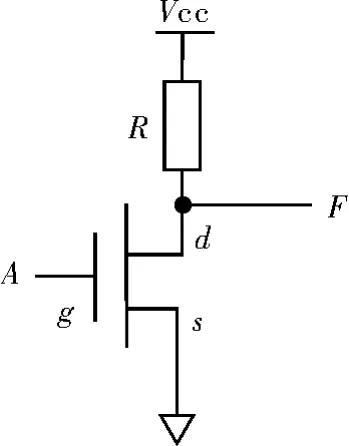
图1 NMOS反相器

学生们会马上说到压敏电阻，这个主意很好，但当被告知压敏电阻不能与NMOS管集成在一起时，学生们陷入了沉思，产生了认知冲突，出现了“愤悱”状态。教师可及时对学生进行启发，并引导学生探究问题，以提高教学效率。

引导学生思考上述问题后，接着介绍PMOS管的特性。如图 2所示［4-6］，若栅极g=0，PMOS管导通，源极s和漏极d之间的电阻很小；若栅极g=1，PMOS管截止，源极s和漏极d之间的电阻很大。由此可见，PMOS管的源极s和漏极d之间的等效电阻就是一个可随输入电压变化而变化的电阻，这正是我们要找的那种电阻。

图2 PMOS管

继续设问:若把图1中的电阻R换为图2的PMOS管，是否就能满足图1的电路对电阻R的要求？由此引出了CMOS反相器结构。

2 CMOS反相器

把图1中的电阻R换为pMOS管后，就得到图3所示的CMOS反相器电路图［7-8］。若图3的输入A为0，NMOS管Q1截止，PMOS管Q2导通，Q2的源极s和漏极d之间的电阻很小，则输出端通过导通的Q2到电源获得高电平。然而，若图3的输入A为1，NMOS管Q1导通，PMOS管Q2截止，Q2的源极s和漏极d之间的电阻很大，则输出端通过导通的Q1到地得到低电平。因此，Q2起到了图1电阻R的作用，随着输入电平的不同，体现出的电阻值完全不一样，而且输入和输出之间的关系构成了逻辑反相的功能。这就是CMOS反相器的工作原理。

学生自己设问:为什么图3的电路称为CMOS反相器？因为它由两个性质互补的MOS管构成。CMOS的第1个字母C其实是单词Complementary（互补）的首字母。对这样的问题学生稍加思考就能领悟。

让学生相互讨论:对比NMOS反相器，CMOS反相器有何优点？从图3可以看到，不管输入的逻辑电平是什么，任何时候CMOS反相器中总是只有一个MOS管导通，另一个MOS管截止，从电路的电源到地是没有直流通路的。因此，CMOS反相器的静态功耗比NMOS反相器的静态功耗要低得多。这就是CMOS反相器得以广泛应用的原因。

图3 CMOS反相器

再设问:CMOS反相器的电路构成有何特点？从图3知道，为了使输入端同时控制两个MOS管的开和关，输入端就必须同时连接两个MOS管的栅极，并且NMOS管的源极接地，PMOS管的源极接电源，然后漏极连在一起并作为反相器的输出。

学生掌握了上述CMOS反相器的构成和工作原理后，有些喜欢思考的学生会主动向教师提出下列问题（几乎每年讲授数字逻辑设计及应用课程时都有学生提问）:PMOS管在上面，NMOS管在下面，构成了CMOS反相器，若交换两者的位置，如图4所示，NMOS管在上面，PMOS管在下面，是否就能构成缓冲器呢？为什么？

图4的电路初看好像是没有问题，但仔细分析却是有问题的。教师没有马上告知学生答案，而是先让学生思考，然后才引导学生进一步分析。

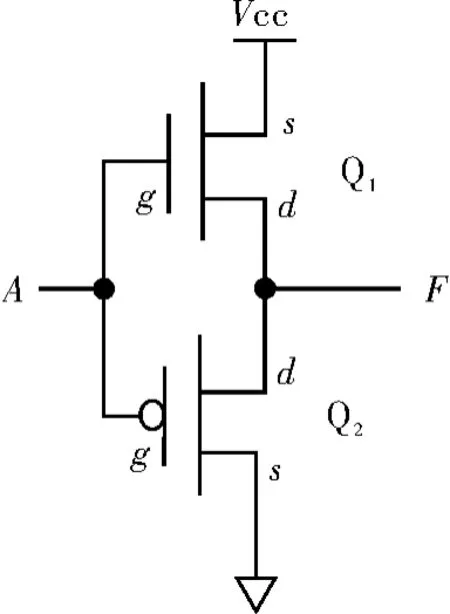
图4 假设的逻辑门

实际上，如图4所示，输入A=1时，PMOS管Q2的Vgs>0，Q2截止；NMOS管Q1的Vgs≈0，Q1也截止，因此两个晶体管都截止，输出F呈现高阻态。

同理，输入A=0时，NMOS管Q1的Vgs<0，Q1截止；PMOS管Q2的Vgs≈0，Q2也截止，因此两个晶体管也都截止，输出F也呈现高阻态。所以图4所示的电路是不可能工作的。

3 CMOS传输门

再让学生相互讨论:从图3可知，NMOS管和PMOS管串接时构成了CMOS反相器。若把NMOS管和pMOS管并接起来，如图5所示［9-10］，将构成什么功能的器件？这时学生再次产生认知冲突，再次出现了“愤悱”状态。

图5 两个MOS管并接

为了分析图5电路的功能，增加一个CMOS反相器U1，得到如图6所示电路，其中C′（或）表示C的反相。

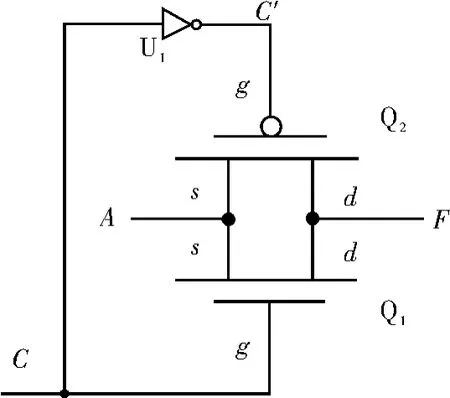
图6 CMOS传输门

1）当控制输入C=1，C′=0，若输入A=1，则图6的Q1截止，Q2导通，输出F=1；若输入A=0，则图6的Q2截止，Q1导通，输出F=0。因此，输入C=1时，输出F=A。

2）当控制输入C=0，C′=1，不管输入A是什么逻辑电平，图6的Q1和Q2都截止，因此，输出F呈现高阻态。

综合上述分析，图6就是一个CMOS三态传输门。学生会自问:“三态”是指什么？如前所述，当图6的输入C=1时，输出F=A，若输入低电平，则输出是低电平，若输入高电平，则输出是高电平；当图6的输入C=0时，输出F呈现高阻态。因此，根据不同的输入逻辑电平，传输门的输出将出现三种状态之一，故“三态”就是指逻辑高电平态、逻辑低电平态和高阻态，学生就能马上领会。

让学生分析:CMOS三态传输门有什么特点？由图6可知，PMOS管传输逻辑高电平，NMOS管传输逻辑低电平，当控制输入 C=1时，两个 MOS管总有一个是导通的。由于MOS管的源极s和漏极d结构上是对称的，因此CMOS三态传输门还是一个双向传输器件。

还可以继续设问:

1）再进一步延伸，CMOS与非门如何构成？

2）CMOS或非门又是如何实现的？

3）能否总结出其他逻辑门的构成规律？

上述从一个简单问题的提出和解决就可以延伸出一系列相关问题，通过对问题由简单到复杂的逐层探究，提高了学生学习课程的兴趣，学生把握了知识的来龙去脉，掌握了相关知识的相互关系。

4 结束语

CMOS反相器和传输门是数字逻辑设计及应用课程中最基本的逻辑门电路，传统的传授式方法是教师直接告诉学生CMOS反相器和传输门的构成结论，学生被动地接受知识，对得到的结论印象不深刻，不知晓其原因。本文运用启发式和讨论式教学方法，从NMOS反相器存在的问题出发，探究了CMOS反相器和传输门的构成过程，有助于学生的知识构建，取得了良好的效果。

［1］范钦珊，鞠平，伍贻兆.提高课堂教学质量是提高教育质量的关键［J］.中国大学教学，2003（11）:4-7.

［2］Richard R.Spencer，Mohammed S.Ghausi.电子电路设计基础［M］.张为，译，北京:电子工业出版社，2005.

［3］Sung-Mo Kang，Yusuf Leblebici，Chulwoo Kim.CMOS数字集成电路:分析与设计［M］.4版（英文版）.北京:电子工业出版社，2015.

［4］阎石.数字电子技术基础［M］.5版.北京:高等教育出版社，2006.

［5］William J.Dally，R.Curtis Harting.Digital Design:A systems approach［M］.Cambridge University Press，2012.

［6］毛法尧.数字逻辑［M］.2版.北京:高等教育出版社，2008.

［7］王毓银.数字电路逻辑设计（脉冲与数字电路）［M］. 3版.北京:高等教育出版社，1999.

［8］龙忠琪，龙胜春.数字集成电路教程［M］.2版.北京:科学出版社，2007.

［9］WAKERLY J.数字设计:原理与实践（原书第4版）［M］.林生，译，北京:机械工业出版社，2007.

［10］姜书艳.数字逻辑设计及应用［M］.成都:电子科技大学出版社，2014.

Teaching Practice for CMOS Inverter and Transmission Gate

TANG Puyinga，JIANG Shuyanb
（a.School of Optoelectronic Information；b.School of Automation Engineering，University of Electronic Science and Technology of China，Chengdu 610054，China）

CMOS inverter and transmission gate are the basic logic gate circuits in digital logic design and its application.They are also the digital circuits with which students first come into contact.Correctly understanding the inverter and the gate is the basis of learning other logic gate circuits.From the question existed in NMOS inverter to the formation of CMOS inverter and transmission gate，heuristic and discussion-based teaching method is applied in the course teaching.The process of problem solving is presented by guiding the students to analyze problems step by step.The practice results have shown that students’interest in learning the course has been improved，and that the knowledge of context and the related knowledge of mutual relations have been mastered.

digital circuit；inverter；transmission gate；heuristic teaching

TN79；G642.4

A

10.3969/j.issn.1672-4550.2016.05.026

2015-04-10；修改日期：2015-10-14

电子科技大学教学改革研究项目（2013XJYSL011）。

唐普英（1965-），男，博士，副教授，主要从事电子技术的教学与研究工作。