11位多数判决器的层次化设计
方 藤,唐普英(电子科技大学 光电信息学院,成都 610054)
11位多数判决器的层次化设计
方 藤,唐普英
(电子科技大学 光电信息学院,成都 610054)
利用模块层次化的多数判决算法,设计了11位多数判决器的最简化组合逻辑电路。首先对11个输入变量进行分组,分别对每组变量按一定算法进行设计,然后按层次对变量数进行递进式缩减,最后根据多数判决的要求对所得6个结果变量进行处理以确定输出结果。为验证该设计的有效性,利用Modelsim仿真软件对电路功能进行抽样性检验测试仿真。仿真结果表明,设计的逻辑电路在保证成本最低的情况下实现了11位多数判决的功能。
11位多数判决器;模块层次化设计;逻辑电路;仿真测试
在数字逻辑设计与应用课程中,功能层次化、结构模块化的设计思想有助于解决设计功能特殊、结构复杂的逻辑电路时产生的难题,在一些多输入集成电路(如A/D转换电路)中这种思想体现尤甚。该思想主要是先将多个输入变量分成若干组(每组变量数小于4为宜),再分别对每组按一定算法进行设计(其设计结果的变量数应小于输入的变量数),然后将这些结果变量汇总,再按一定算法对结果变量进行设计(如二次设计的变量数仍较多,则再进行一次或多次分组设计直至汇总得到的结果变量数合理),最终得到最后的输出。故本文在于以一种11位多数判决器的模块层次化设计方案为例,以深化模块层次化的设计理念在逻辑电路设计中的应用。
该判决器并行输入为11位的向量,若其中1的数量超过0的数量,输出设置为1。考虑到实际中可能会存在无效信号的干扰,加一片选输入端Data_ Ready,当其信号为1时才对输入数据进行检查。
若类似于3位多数判决器一样列出其真值表,然后根据真值表写出逻辑功能表达式[1-3],那么11位的多数判决器将会形成一个211=2 048行的真值表,可以想象通过真值表来得出逻辑表达式几乎是不可能的。
所以本课题在于设计一种简化的多数判决(majority vote)算法,通过这个算法对输入向量进行分模块化处理[2-3],并分层次得出相应的电路逻辑 关 系[4-6]。
1 方案设计
1.1 方案介绍
Data_Ready信号为1时,才对输入数据进行检查,那么Data_Ready信号输入端可以作为此判决器的使能端(高电平使能)。
对于11位的并行输入数据A,B,C,D,E,F,G,H,I,J,K进行分组分层次处理。
第一层次:将 11位数据分为(A,B,C)、(D,E,F)、(G,H,I)、(J,K)4组。在前3组数据中,对其中1的数量进行编码并向下一层次输出,(J,K)组数据留在下一层次进行处理。
第二层次:将第一层次中(A,B,C)、(D,E,F)两组的输出结果X1,Y1,X2,Y2并为一组,(G,H,I)组的输出结果X3,Y3与第一层次中未处理的(J,K)并为一组。在这两组数据中根据输入的编码对1的数量进行统计并再次进行编码对下一层次输出。
第三层次:对上一层次中第一组的输出结果Q1,Q2,Q3和第二组的输出结果Q4,Q5,Q6所反映的1的数量(也就是11位输入数据中1的数量)进行统计整理,并根据多数判决的原理将相应的结果输出。
层次结构图如图1所示。

图1 11位多数判决器的层次结构图
1.2 各层次的具体实现
1)第一层次
(A,B,C)、(D,E,F)、(G,H,I)、(J,K)4组中,每组必须对下一层次输出该组中1的个数。
对于第一组(Part1),以2位二进制编码(X1Y1)来表征三位中1的个数,如表1所示。

表1 Part1输出编码表
由表1可得:
X1=A·B+B·C+A·C
Y1=A′·B′·C+A′·B·C′+A·B′·C′+ A·B·C
加上Data_Ready使能端,表达式为:
X1=A·B·Data_Ready+B·C·Data_Read+ A·C·Data_Ready
Y1=A′·B′·C·Data_Ready+A′·B·C′· Data_Ready+A·B′·C′·Data_Ready+A·B· C·Data_Ready
对于D,E,F(Part2)和G,H,I(Part3)两组,用第一组的方法,可得:
X2=D·E·Data_Ready+E·F·Data_ Ready+D·F·Data_Ready
Y2=D′·E′·F·Data_Ready+D′·E·F′· Data_Ready+D·E′·F′·Data_Ready+D·E· F·Data_Ready
X3=G·H·Data_Ready+H·I·Data_Ready+ G·I·Data_Ready
Y3=G′·H′·I·Data_Ready+G′·H·I′· Data_Ready+G·H′·I′·Data_Ready+G·H·I· Data_Ready
对于最后一组(J,K),在下一层次中处理。
2)第二层次
对第一层次中输出的X1,Y1,X2,Y2,X3,Y3和输入端口J,K进行处理,
类似地,用3位二进制编码(Q1Q2Q3)来表征X1,Y1,X2,Y2,也就是A,B,C,D,E,F中1的个数,如表2所示。

表2 Part4输出编码表
根据表2可得:
Q1=X1·Y1·Y2+Y1·X2·Y2+X1·X2
Q2=X1·X2′·Y2′+X1·Y1′·X2′+X1′·Y1′· X2+X1′·X2·Y2′+X1′·Y1·X2′·Y2+X1·Y1· X2·Y2
Q3=Y1⊕Y2
用3位二进制编码(Q4Q5Q6)来表征X3,Y3,J,K中1的个数,同法可得:
Q4=X3·Y3·K·Data_Ready+X3·Y3·J· Data_Ready+X3·J·K·Data_Ready
Q5=X3′·Y3·K·Data_Ready+X3·J′·K′· Data_Ready+X3·Y3′·J′·Data_Ready+X3′· J·K·Data_Ready+X3·Y3′·K′·Data_Ready+ X3′·Y3·J·Data_Ready
Q6=Y3·J′·K′·Data_Ready+Y3′·J′·K· Data_Ready+Y3·J·K·Data_Ready+Y3′·J· K′·Data_Ready
3)第三层次
对第二层次中输出的Q1,Q2,Q3,Q4,Q5,Q6进行统计处理得出输出结果Z,如表3所示。
表3对应的逻辑表达式为:
Z=Q1′·Q2′·Q3·Q4·Q6+Q1′·Q2·Q4· Q5′+Q1′·Q2·Q3·Q4+Q1′·Q2·Q3·Q5·Q6+ Q1·Q2′·Q4′·Q5+Q1·Q2′·Q4·Q5′+Q1·Q2′· Q3·Q6+Q1·Q2
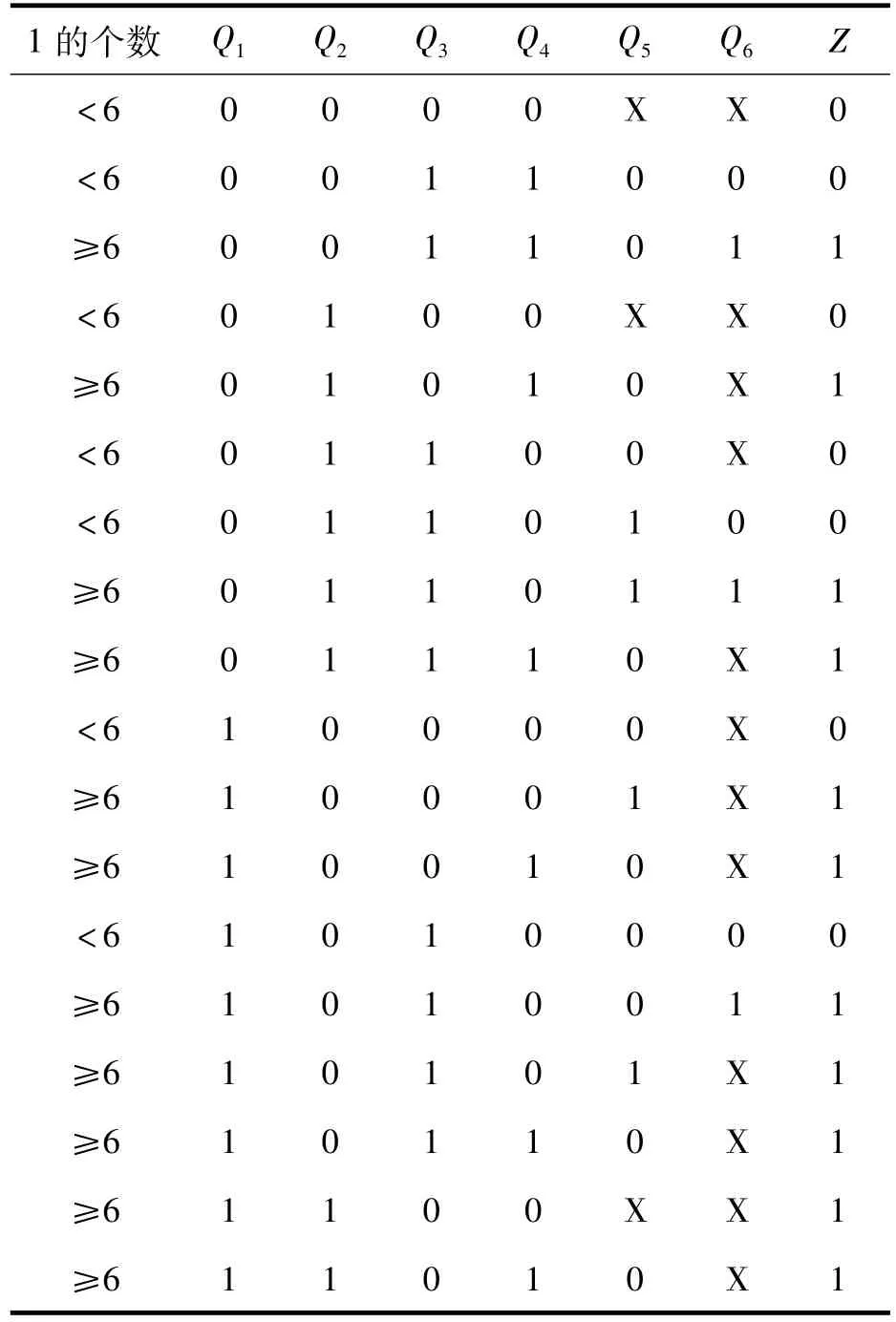
表3 Part6输出编码表
4)逻辑框图
将以上各部分的逻辑关系按照图1进行合并,得到多数判决器的总逻辑框图,如图2所示。
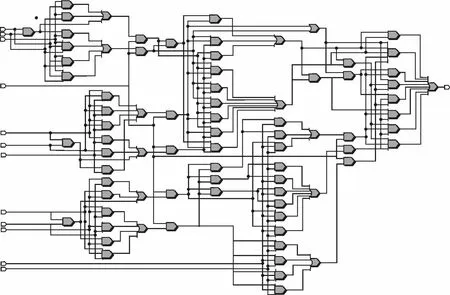
图2 系统总逻辑框图
2 仿真及结果分析
根据以上方案设计,在Modelsim软件中编写相应Verilog程序并编译、仿真[7],在A~K端口依次加入不同周期的时钟信号,进行抽样性的观察得波形图如图3和图4所示。

图3 Data_Ready信号有效时波形图
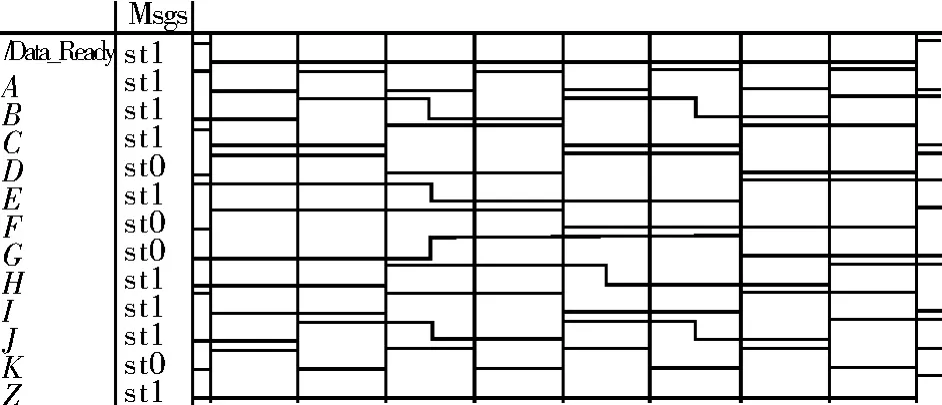
图4 Data_Ready信号无效时波形图
分析图3中波形可知:Data_Ready信号有效(Data_Ready=1)时,对应输入的输出为Z,如A,B,C,D,E,F,G,H,I,J,K分别为0,1,0,1,1,1,0,1,0,1时,输出Z=1,符合11位多数判决器的功能。
分析图4中波形可知:Data_Ready信号无效(Data_Ready=0)时,输出Z恒为0,满足Data_ Ready=0时不检查输入数据的要求。
3 结束语
若直接写出该11位多数判决器211行的真值表,并根据真值表[8-10]画出26×25的卡诺图,根据设计要求,此卡诺图中将会有=1 024个格中填1。为估算其成本,假设这1 024个格子中每4个“1”相邻可被圈在一起,那么至少会形成256个圈,即至少会用到256个逻辑门(实际上不是每4个都可以被圈在一起,这可能导致成本更高),这已进入大规模集成电路的范围,而且从真值表到卡诺图,再到逻辑表达式的相关的处理工作也相当繁冗。而本文所设计的多数判决器方案只用到了80个逻辑门,属于中规模集成电路,大大降低了成本。
此外,以此11位多数判决器的模块层次化设计方案为例,通过多数判决算法的优化和逻辑运算的简化,层次分明、结构清晰,突出了这种分模块分层次的组合逻辑电路设计理念的优点。相信在其他具有特殊功能及应用的逻辑电路的设计中,模块层次化的设计理念可以得到广泛的运用与推广。
[1]WAKERLYJ F.数字设计——原理与实践[M].北京:高等教育出版社,2007.
[2]刘占文,高飞,王轶萍,等.判奇电路实现方法探讨[J].机械工程与自动化,2013,19(17):13-18.
[3]刘祖刚,曾梅香.关于组合逻辑电路设计方法与设计技巧[J].高等函授学报(自然科学版),1995(4): 33-36.
[4]王丽萍,徐开琴.数字逻辑电路设计的两个重要问题[J].白城师范学院学报,2008,22(6):26-30.
[5]孙津平.基于组合逻辑电路实现方法的探究[J].电子设计工程,2011,19(8):151-153.
[6]库少平,胡伟莉.数字逻辑电路的竞争与险象分析[J].电子工艺技术,2003,24(4):170-171.
[7]Model Technology Corporation.ModelSim 5.4 User Manual[Z].Portland,USA:2000.
[8]周宦银,刘家华.卡诺图法化简多变量逻辑函数的探讨[J].电子工程师,2006,32(7):30-31.
[9]韩新风,高伟霞.卡诺图在数字电路教学中的应用[J].重庆文理学院学报(自然科学版),2011,30(6):74-77.
[10]蒋志勇,陈锡华,熊川.卡诺图在多变量逻辑函数化简中的应用[J].桂林航天工业高等专科学校学报,2006,11(4):4-5.
Hierarchical Design of 11 bit Majority Judgment
FANG Teng,TANG Puying
(School of Optoelectronic Information,University of Electronic Science and Technology of China,Chengdu 610054,China)
By using the modularized and hierarchical algorithm of majority judgement,the most simplified combination logic diagram of digital circuit of 11bit majority judgment is designed.That is,11 input variables are divided into groups and the logic relationships in each group are structured respectively.Then,the numbers of the variables are reduced hierarchically by step.Finally,the output is decided after handling the 6 outcome variables via majority judgment.To verify the effectiveness of the design,the programme is composed and its function is tested and checked by samples in simulation software Modelsim.The simulation result shows that the designed digital circuit can realize the function of 11bit majority judgment at the lowest cost.
11bit majority judgment;modularized and hierarchical design;logiccircuit;simulation and test
TN79+1
A
10.3969/j.issn.1672-4550.2016.05.013
2015-05-18;修改日期:2015-06-14
方 藤(1995-),男,学士,光电专业。

