复函数矩阵的向量及矩阵导数的性质

杜 鹃, 冯思臣, 谭仁俊

(成都理工大学 管理科学学院，成都 610059)



复函数矩阵的向量及矩阵导数的性质

杜 鹃, 冯思臣, 谭仁俊

(成都理工大学 管理科学学院，成都 610059)

复函数已经广泛应用于自然科学各领域，有必要探讨复函数矩阵的各种分析性质，特别是对向量与矩阵的导数的研究。本文以实函数矩阵性质为基础，针对复函数矩阵的特征，引入复函数矩阵及其极限、连续性、导数、积分等概念或定义。以综合类比与推理研究的方法，推导出复矩阵函数的逆、迹的导数的算法，尤其是复向量数量函数、复多元向量函数、复向量复合函数对向量的导数，以及复合复函数、复二次型的导数的性质；进一步揭示了复矩阵函数、复矩阵函数对矩阵的导数以及迹、行列式导数的重要性质，也得到了复矩阵函数、复向量矩阵函数的全微分的算法。研究结果表明复函数矩阵对向量与对矩阵的导数的算法虽然源于实函数矩阵的导数算法，但却发展出非常多的、更广泛的不同性质。

复向量；复矩阵；复函数矩阵；矩阵函数

1 预备知识

函数矩阵的性质在控制论、信息处理、图像识别领域有着重要作用，相关结论都主要针对实变量的函数矩阵[1]；而复变量的函数矩阵有着重要性质。本文主要讨论复变量的函数矩阵，给出函数矩阵解析性，以及对向量、矩阵变量的导数性质。下面的定义将实变量的函数矩阵性质拓宽到复函数矩阵。

定义1 若矩阵A=(aij(z))m×n，其中aij(z)是复函数，即

称它为复函数矩阵[2,3]。

首先给与实函数有类似结果的复函数矩阵极限、连续、导数及积分等概念。

c. 若aij(z)在z=z0处可导或者在区域D上解析(i=1,2,…,m;j=1,2,…,n)，则称A(z)在z=z0处可导或在区域D上解析。记

定义2

c. 设矩阵H是以复矩阵Z∈Cm×n为自变量的s×t复多元函数矩阵[8]

hkq(Z)以Z=(zij)m×n的元素为变量的m×n元复函数，则定义

其中

d. 设H=(hij)m×n,hij=hij(Z), Z=(z1,z2,…,zn)Τ，

则H的全微分为dH=(dhij)m×n。

由于复变函数的解析性不同于实函数的可导性，因而使解析函数有广泛的应用。以下主要给出复函数矩阵导数的结论。

引理1 复函数矩阵A(z),B(z)在D上解析，则

a. (A(z)+B(z))′=A′(z)+B′(z)。

b. (A(z)B(z))′=A′(z)B(z)+A(z)B′(z)。

c. (k(z)A(z))′=k(z)A′(z)+k′(z)A(z)[9]。 引理2 设A(z)是复函数矩阵，A(z)=(aij(z))n×n，

a. 若A(z)与A-1(z)都在区域D 上解析，则

证明

a. ∵A(z)A-1(z)=I，由复函数导数的性质得A′(z)A-1(z)+A(z)(A-1(z))′=0。

∴A(A-1(z))′=-A′(z)A-1(z),即

引理3 设复向量函数h(Z)=h(z1,z2,…,zn),f(Z)=f(z1,z2,…,zn), 其中Z=(z1,z2,…,zn)Τ, 则

证明b由定义2-a有

=(fz1h,fz2h,…,fznh)Τ+(fhz1+fhz2,…,fhzn)Τ

类似可得a、c。

2 主要结果

定理2 设A=(aij)n×n为复数矩阵，f(Z)=ZTAZ，其中Z=(z1,z2,…,zn)Τ，则

证明

=AZ+ATZ=(A+AT)Z

定理3W=f(Z)=(w1,w2,…,wn)Τ,Z=(z1,z2,…,zn)。

其中w1=f1(Z)=f1(z1,z2,…,zn);w2=f2(Z)=f2(z1,z2,…,zn); …;wn=fn(Z)=fn(z1,z2,…,zn)。 则

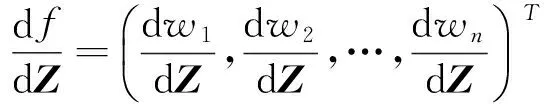
证明 由定义2-b。

定理4

证明

=((0,0,…,zj,0,…,0)AZ+⋮i列ZΤAΤ(0,0,…,0,zj,0,…,0)Τ)m×n⋮i列

=((zjai1,zjai2,…,zjain)(z1,z2,…,zn)Τ+ZΤ(zjai1,zjai2,…,zjaim)Τ)m×n

=2AZZΤ。

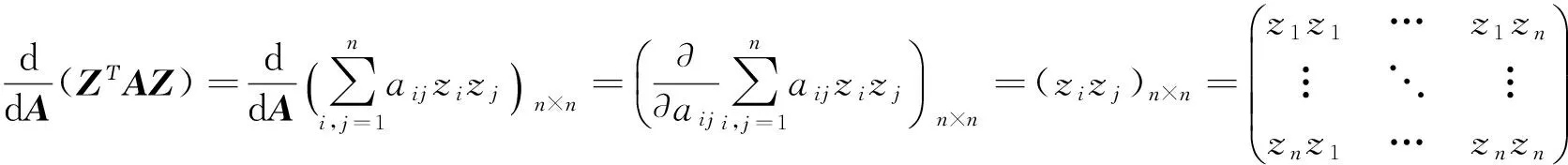
=(z1,z2,…,zn)Τ(z1,z2,…,zn)=ZZT。

定理5 设f(w)是函数向量w=(w1,w2,…,wn)Τ的函数，而wi=wi(Z)，其中

证明

推论

证明

证明 由定义2-c,

3 结 论

从上面的结论可以得出复函数矩阵的分析性质是实函数矩阵分析性质的进一步拓展，是由复函数与实函数的区别和联系产生的。

复函数结合矩阵论，在现代许多科学领域都有着比它们各自单独使用时更广泛的应用。把这两者有效地结合起来进行进一步的研究是一个新课题，在实函数矩阵论范围内它将会有更多的新成果，这些方法和结果在实际应用中，会使得所需要的运算更加高效与快捷。

[1] 杜鹃，冯思臣．复矩阵的Givens变换及其QR分解[J]．成都理工大学学报(自然科学版)，2011，38(6)：693-696.

Du J, Feng S C. Givens transformation and QR factorization of complex matrix[J]. Journal of Chengdu University of Technology (Science & Technology Edition), 2011, 38(6): 693-696. (In Chinese)

[2] Li X H, Fan H. QR factorization based blind channel identification and equalization with second-order statistics[J]. IEEE Trans Signal Process, 2000, 48(1): 60-69.

[3] 戴中林．矩阵函数f(A)的计算方法[J]．大学数学，2012，28(1)：144-150.

Dai Z L. Computational method of matrix functionf(A)[J]. College Mathematics, 2012, 28(1): 144-150. (In Chinese)

[4] 杜鹃，范啸涛，杨建康．自伴矩阵与Hemite二次型[J]．成都理工大学学报(自然科学版)，2007，34(4)：478-481.

Du J, Fan X T, Yang J K. Independent companion matrix and Hermite quadratic form[J]. Journal of Chengdu University of Technology (Science & Technology Edition), 2007, 34(4): 478-481. (In Chinese)

[5] Zhang X D, Li J S. Spectral radius of non-negative matrices and digraphs[J]. Acta Mathematica Sinica, 2002, 18(2): 293-300.

[6] 方保镕，周继东，李医民．矩阵论[M]．北京：清华大学出版社，2013:255-263.

Fang B R, Zhou J D, Li Y M. Matrix Theory[M]. Beijing: Tsinghua University Press, 2013: 255-263. (In Chinese)

[7] 杜鹃，冯思臣，谭仁俊．复矩阵的对称满秩分解[J]．郑州大学学报(理学版)，2011，43(1)：4-6.

Du J, Feng S C, Tan R J. Decomposition of symmetry full rank matrices on complex matrix[J]. Journal of Zhengzhou University (Natural Science Edition), 2011, 43(1): 4-6. (In Chinese)

[8] 杨中原，傅英定，黄廷祝．逆M-矩阵的一些性质及应用[J]．电子科技大学学报，2005，34(5)：713-716.

Yang Z Y, Fu Y D, Huang T Z. Some properties of inverse M-matrices and their applications[J]. Journal of University of Electronic Science and Technology of China, 2005, 34(5): 713-716. (In Chinese)

[9] 周富照，郭婧，黄雅．一类矩阵方程的对称正交对称解的迭代法研究[J]．郑州大学学报(理学版)，2009，41(3)：1-4.

Zhou F Z, Guo J, Huang Y. An iterative method for the symmetric ortho-symmetric solutions of a class of matrix equation[J]. Journal of Zhengzhou University (Natural Science Edition), 2009, 41(3): 1-4. (In Chinese)

[10] Gale J E, Miana P J, Pena A. Hermite matrix-valued functions associated to matrix differential equations[J]. Constructive Approximation, 2007, 26(1): 93-113.

[11] 夏璇，毕公平．复合矩阵及其在Hermite矩阵中的应用[J]．江西师范大学学报(自然科学版)，2009，33(3)：312-316.

Xia X, Bi G P. Compound matrix and its application to Hermite matrix[J]. Journal of Jiangxi Normal University (Natural Sciences Edition), 2009, 33(3): 312-316. (In Chinese)

[12] 于江明，谢清明．次正定Hermite矩阵次Schur补的性质[J]．数学杂志，2006，26(2)：185-190.

Yu J M, Xie Q M. Some properties for sub-Schur complement of metapositive definite sub-Hermite matrices[J]. Journal of Mathematics, 2006, 26(2): 185-190. (In Chinese)

Properties of derivative of complex functions matrix of vector and matrix

DU Juan, FENG Si-chen, TAN Ren-jun

CollegeofManagementScience,ChengduUniversityofTechnology,Chengdu610059,China

Owing to wide application of complex function to most fields of nature sciences, it is necessary to discuss all the analysis properties of complex function matrix, especially the derivative of complex function to the vector variables and matrix variables. Based on the properties of real function matrix, combined with the characters of complex function matrix, the concepts of limits, continuity, derivative and integral are defined. Synthetic analogy and reasoning research are used to deduce the algorithms of derivative of the inverse and trace of complex matrix function, especially the derivative of complex vector quantity function, complex function of several vector variables, and complex vector compound function to vector and properties of derivative of compound complex function and complex quadratic form. Furthermore, the important properties of the derivative of complex matrix function, complex matrix function of complex matrix to matrix and the properties of the derivative of the trace are discovered. Also, the algorithms on the total differentiation of complex vector matrix function and complex matrix function are deduced. It proves that the derivative of complex function matrix to the vector and matrix origins from the derivative of real function matrix, it develops more and wider different properties.

complex vector; complex matrix; complex function matrix; matrix function

10.3969/j.issn.1671-9727.2016.05.15

1671-9727(2016)05-0635-06

2015-05-23。

国家自然科学基金项目(1047112); 四川省教育厅自然科学重点资助项目(08ZA114)。

杜鹃(1961-)，女，教授，主要研究方向:数值代数, E-mail：dj4078@126.com。

O151.21

A