并联有源滤波器补偿容性非线性负载的研究

张 涛

（易事特集团股份有限公司，广东 东莞 523808）

并联有源滤波器补偿容性非线性负载的研究

张 涛

（易事特集团股份有限公司，广东 东莞 523808）

本文针对实际工程应用中并联型有源滤波器补偿UPS容性非线性负载时产生振荡这一问题，在详细分析UPS容性非线性负载特性的基础上，提出了基于FFT的有选择谐波补偿方案以抑制系统谐振。研制一台50kVA三相四线并联有源滤波器，对200kVA十二脉波相控整流装置的UPS进行谐波补偿实验，实验结果验证了补偿方案的有效性。

并联有源电力滤波器；容性非线性负载；FFT；有选择谐波补偿

目前大量使用的电子设备，例如大功率可控硅相控整流电路，交交变频器，工业用电弧炉，开关电源以及其他非线性负载产生了大量的谐波导致了严重的电网污染。并联有源电力滤波器（Shunt Active Power Filter）作为一种有效的被动式谐波治理方案，近年来越来越受到人们的重视[1]。

并联型有源电力滤波器工作时，通常控制为一个谐波电流源[2]，适合补偿电流型谐波源，如阻感型负载，不适合补偿电压型谐波源，如电容滤波型整流负载[3]。但是，并联有源电力滤波器在实际工程应用中，不可避免地会遇到补偿电容滤波型整流负载的情况，比如采用相控整流装置的大功率UPS。由于提高功率因数的需要，这些UPS装置在相控整流装置前一般都要安装大的无功校正电容，当并联有源滤波器投入时，如果这些电容和电网电感构成并联谐振回路的固有谐振频率在有源电力滤波器补偿的频率段内，有源电力滤波器输出的补偿电流将会引起系统谐振，这就是并联型有源滤波器补偿容性非线性负载时遇到的典型问题[3]。

很多学者已经认识到这个问题，并提出相应的解决方案。文献[4]中采用检测电网电压的控制方式达到谐波阻尼的目的，但控制方式是在电网电压比较理想的情况下实现谐波阻尼的，没有考虑到现场实际电网电压畸变对控制的影响。文献[5]给出一种补偿负载电流谐波和阻尼谐波放大两种情况时的新型控制策略，并通过实验验证了可行性和有效性，但提出的新控制策略算法较为复杂，并且是基于并联混合型有源滤波器的前提下实现的，无法直接应用于目前的谐波振荡抑制。

本文针对实际工程应用中遇到的并联型有源滤波器补偿UPS容性非线性负载时出现的谐振问题，仔细分析了某种型号 UPS容性非线性负载的特性后，结合现场实际情况，采用基于FFT的有选择谐波补偿方案，消除了系统谐振，最终实验验证了补偿方案的有效性。

1 并联有源滤波器补偿UPS容性非线性负载谐振现象分析

电容中点式三相四线并联有源电力滤波器补偿容性负载现场实验结构图如图1所示。

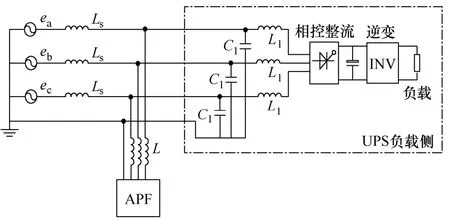
图1 并联有源滤波器补偿UPS容性非线性负载主电路结构图

图1中，ea、eb、ec为三相电网电源相电压，Ls为电网等效电感，L为并联有源滤波器的输出滤波电感，UPS容性负载为电压型谐波源。其中 C1和L1是某种型号200kVA UPS十二脉波相控整流装置前为提高功率因数而安装的滤波电容和电感。因此在并联型有源滤波器实际工作输出谐波补偿电流时，UPS前的C1和电网等效电感 Ls之间便构成了一个并联谐振回路，当谐振频率正好处于有源滤波器补偿的频率范围内时，就会导致相应的谐波放大和负载电流峰值增大[6]。

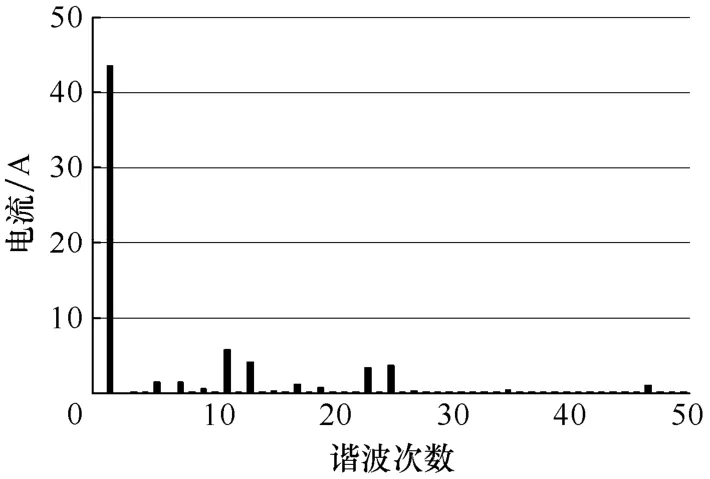
图2 200kVA UPS谐波频谱特性

图2为该型号UPS实际工作时50次以内的电流谐波频谱特性，从图中看出电流谐波主要成分在25次以内，因此要求并联有源滤波器的补偿带宽在25次以上。

图3为并联有源滤波器补偿UPS容性非线性负载谐波频段的模型。

图3中，isn为网侧电流n次谐波分量，icn为有源滤波器输出电流的n次谐波分量，iLn为负载电流中的 n次谐波分量；iLcn表示UPS负载滤波电容支路电流的n次谐波分量，iLon表示UPS负载电容滤波型整流电流中的n次谐波，等效为谐波电流源，上述中，n是一个大于2的整数；此外，G(s)表示从iLn到icn的传递函数。因此网侧等效阻抗Zs，滤波电容阻抗Zc，G(s)分别定义如下：

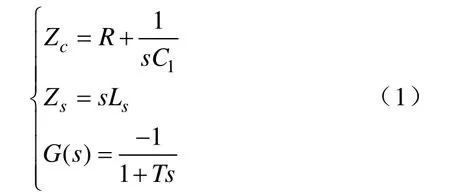
式中，G(s)为一阶惯性环节；T为有源滤波器的延时时间，包括采样滤波延时，谐波计算提取延时，PWM控制延时等。

图3 有源滤波器补偿容性非线性负载的模型（谐波段）

根据图中定义的节点P和O，列出KVL方程和KCL方程

假设有源滤波器能完全补偿负载电流谐波，即：

式（1）至式（4）联立，得到负载谐波源电流iLon到负载电流iLn的传递函数G1(s)：

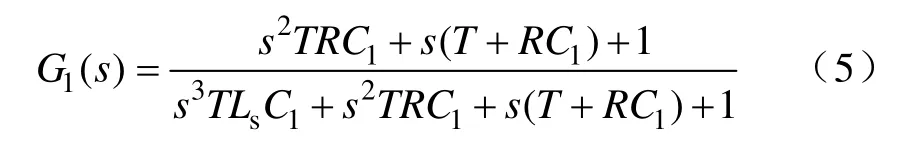
由于电网等效电感Ls在实际工程中是个确定的值，因此 G1(s)的幅频特性就只与 C1的值有关了。系统中Ls为100μH，R为0.5Ω，T为40μs，由式（5）可得C1分别为60μF和600µF时的系统幅频特性图，如图4所示。

从图4中可知，C1为60μF时系统谐振频率约为 2kHz，如果并联有源滤波器谐波补偿次数为 25次，即补偿带宽小于2kHz，当有源滤波器投入工作时输出电流不会出现谐波放大现象。反之当 C1为600μF时，系统谐振频率约为 650Hz，此时谐振点的位置处于并联有源滤波器谐波补偿次数范围内。如果采用基于瞬时无功理论的 ip-iq方法补偿谐波，由于是对负载电流中的谐波进行全带宽补偿，因此当有源滤波器投入输出谐波补偿电流时，将会出现谐波放大现象，引起系统振荡。这也是并联有源滤波器补偿容性非线性负载时不宜直接采用 ip-iq方法补偿谐波的原因。

2 并联有源滤波器补偿容性非线性负载的控制策略

基于上述的分析，UPS滤波电容与电网等效电感存在一个固有的谐振频率，并联有源滤波器的投入极易激励谐振的发生，为避免谐振的发生，一般可以采用以下两类方法[6]。

1）改变原系统的固有谐振频率范围，通常是给并联电容器串接一定的电抗器，改变并联电容器和与系统阻抗的谐振点，以避免谐振[6-7]。

2）要对并联有源滤波器进行改进，变原来的全带宽补偿为有限带宽补偿，有选择谐波次数的补偿，不需给滤波系统提供谐振激励源[6]。

由于在实际工程应用中有源滤波器对补偿对象不能提出要求，无法对UPS负载滤波电容串接电抗器，因此目前最有效的方法是变全带宽补偿为有限带宽补偿，即基于FFT的有选择谐波补偿算法。该算法的原理是，假设系统的谐振频率为ωm，基于FFT算法的有选择谐波补偿带宽为ω1，要求ω1＜ωm，对于低于ω1的谐波分量进行全补偿；对于高于ω1的谐波分量，FFT谐波检测算法乘“0”，即

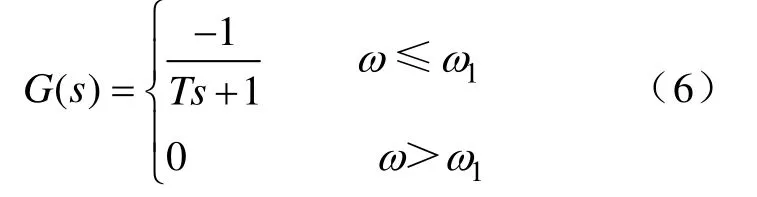
把式（6）代入式（1）和式（5），得到基于FFT有选择谐波补偿算法时的从负载谐波源电流 iLon到负载电流iLn的传递函数G2(s)如式（7）所示。

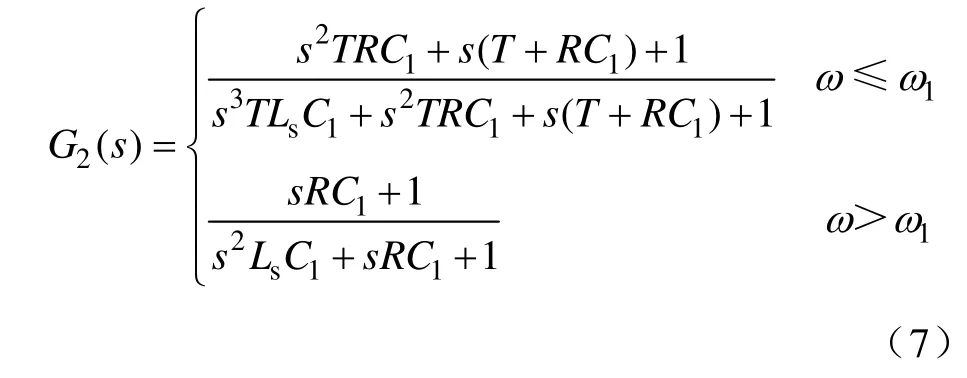
式（7）给出了 FFT有选择性谐波补偿算法与Ls和C1并联谐振频率之间的关系，即当有选择谐波补偿带宽小于或者大于谐振频率时是否会发生谐振现象。G2(s)的幅频特性如图5所示。

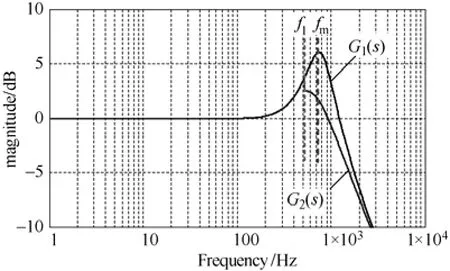
图5 G1(s) & G2(s)的波特图（C1=600μF）

图5中，G1(s)是没有加入FFT算法时系统的幅频特性，G2(s)是加入FFT算法后系统的幅频特性，fm是系统的谐振频率，f1是基于FFT算法时可选择补偿的带宽，且 f1＜fm。由图中可知，对于低于 f1的谐波分量有源滤波器进行了全补偿，FFT谐波检测算法相当于乘“-1”；对于高于f1的谐波分量，FFT谐波检测算法相当于乘“0”，即有源电力滤波器相当于断开状态，因此谐振频率分量被大大地削弱[3]，最终达到了抑制谐振的目的。

3 实验结果

为了验证上述理论分析的正确性，根据现场实际工程应用的需要，由一台50kVA三相四线并联型有源滤波器对某公司某种型号 200kVA十二脉波相控整流装置的UPS进行了谐波补偿实验。

实验控制框图如图6所示，其中主电路参数：电网电压有效值ea、eb、ec为220V，电网频率f为50Hz，电网等效电感Ls=100μH，有源滤波器输出电感L=0.4mH，直流侧电容C为13600μF，直流侧母线电压 Vdc为 780V。主控制芯片采用 TI公司的TMS320F2808 32位DSP，主频100MHz。控制参数：负载电流采样速率25.6kHz，电流环比例增益Kp为100，三角载波幅值Vtri为10V，开关频率fs为15kHz，UPS负载容量为200kVA。图7至图11为实验波形，其中系统谐振频率为650Hz（13次）。

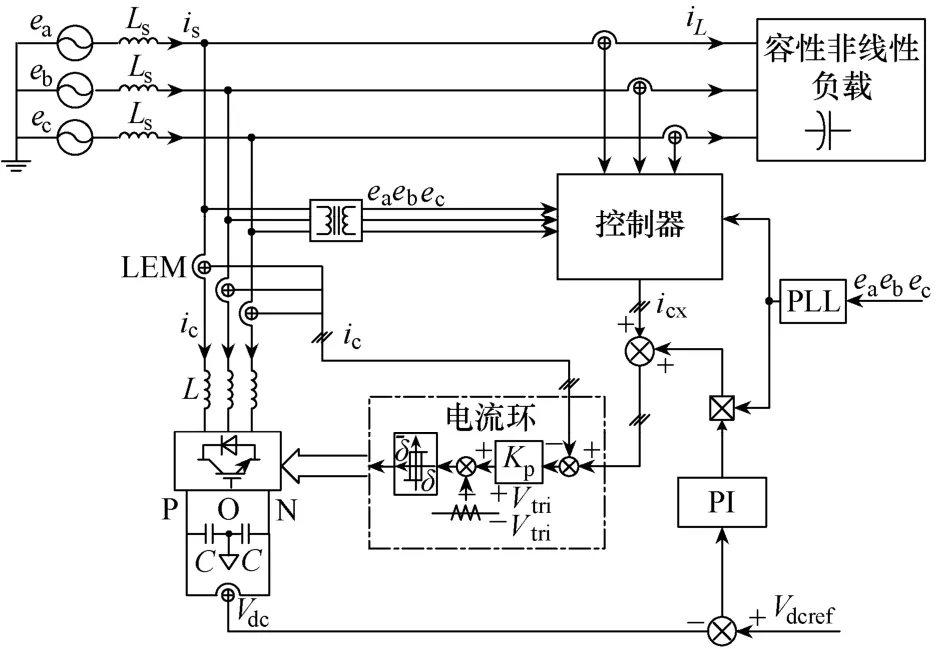
图6 并联有源滤波器补偿容性非线性负载实验框图

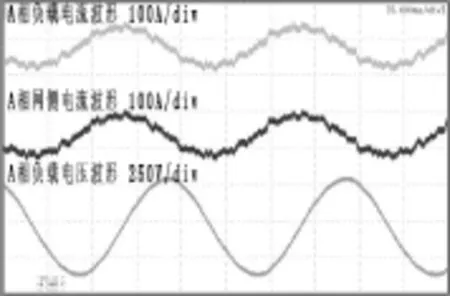
图7 APF不投入只有UPS工作时的波形

图8 APF投入时且采用基于瞬时无功理论的ip-iq算法补偿UPS容性负载时的谐振波形

图7是并联有源滤波器没有投入之前只有UPS工作时的波形，可以看出此时系统稳定，电网电压也没有畸变。

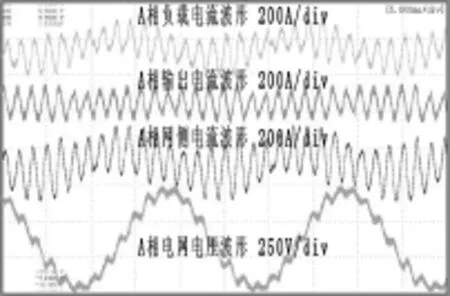
图9 APF投入时且采用基于FFT算法补偿UPS容性负载时的谐振波形（补偿次数为25次）

图10 APF投入时且采用基于FFT算法补偿UPS容性负载时的谐振波形（补偿次数为13次）

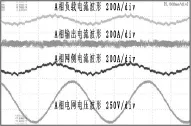
图11 APF投入时且采用基于FFT算法补偿UPS容性负载时没有发生谐振的波形（补偿次数为11次）

图8是并联有源滤波器投入时采用基于瞬时无功理论的 ip-iq方法进行谐波补偿时的波形，由于是对负载电流中的谐波进行全带宽补偿，因此在有源滤波器投入时系统出现了严重的谐振，网侧电流THD大于100%，波形畸变很严重。

图9是并联有源滤波器投入时采用基于FFT算法进行谐波补偿，且补偿次数为25次时的波形，从图9可见，由于补偿带宽大于系统谐振频率（650Hz），有源滤波器投入时系统也出现了严重的谐振。

图 10是并联有源滤波器投入时采用基于 FFT算法进行谐波补偿，且补偿次数为13次时的波形，由于补偿带宽正好等于系统谐振频率，因此仍然会引起系统谐振。

图11是FFT有选择谐波补偿次数为11次时的波形。由于补偿带宽小于系统谐振频率 650Hz（13次），即只补偿到谐振频率点之前的谐波，因此系统稳定不会发生谐振，同时经实验测试，补偿后网侧电流THD小于10%，同图8中采用基于瞬时无功理论的ip-iq方法谐波方案比较（THD大于100%）具有更好的补偿效果。

因此，本文提出的补偿方案不仅可以抑制系统谐振而且具有良好的补偿效果，进一步验证了方案的可行性。

4 结论

本文针对实际工程应用中并联型有源滤波器补偿UPS容性非线性负载时产生振荡这一问题，提出了一种基于FFT的有选择谐波补偿以抑制系统谐振的方案，并从理论上分析了该种控制策略的可行性，最终通过实验结果验证了理论分析的正确性。

［1］周导，陈敏，张涛，等.并联有源电力滤波器谐波畸变率的解析算法［J］.电力电子技术，2010，44（7）：12-14.

［2］仇志凌，杨恩星，孔洁，等.基于LCL滤波器的并联有源电力滤波器电流闭环控制方法［J］.中国电机工程学报，2009，18（18）：15-20.

［3］鞠建永.并联有源电力滤波器工程应用关键技术的研究［D］.杭州：浙江大学，2009.

［4］Wu Longhui，Zhuo Fang，Zhang Pengbo，et al.Stability Analysis and Controller Design of Hybrid Compensation System with Parallel Active Power Filter and Parallel Capacitors［J］.in Power Electronics Specialists Conference，2007.PESC 2007：IEEE，2007.

［5］武健，何娜，徐殿国.无变压器型并联混合有源滤波器设计及应用［J］.中国电机工程学报，2008，12（12）：88-94.

［6］赵文强.并联型电力有源滤波器应用若干关键技术研究［D］.杭州：浙江大学，2010.

［7］王兆安，杨君，刘进军.谐波抑制和无功功率补偿［M］.北京：机械工业出版社，1998.

Study of Compensation for Capacitive Nonlinear Load in Active Power Filter

Zhang Tao
(East Group Co., Ltd, Dongguan, Guangdong 523808)

It is a serious resonance phenomenon happened when compensating capacitive nonlinear load for active filter in practical application field.The paper proposed a method of selective harmonic compensation based on FFT algorithm after analyzing the load features of UPS capacitive nonlinear load.Finally, the experimental results of a 50kVA shunt active filter for compensating a 200kVA UPS capacitive nonlinear load with phase-controlled rectifier equipment are given to verify effectiveness of the proposed study.

APF; capacitive nonlinear load; FFT; selective harmonic compensation

张 涛（1982-），男，甘肃省天水人，硕士，工程师，主要研究方向为有源滤波器，逆变器并联等。