电力变压器零序电抗计算及仿真

刘力强 王春钢

（保定天威保变电气股份有限公司，河北 保定 071056）

电力变压器零序电抗计算及仿真

刘力强 王春钢

（保定天威保变电气股份有限公司，河北 保定 071056）

论述了变压器零序电抗与变压器磁路、联接组别、变压器结构等的关系，并给出了不同结构变压器零序电抗的计算方法。

零序电抗；短路阻抗；激磁电抗；磁路；联接组别

为了保证电力系统和它的各种电气设备的安全运行，必须进行各种不对称故障的分析和计算，通常采用对称分量法把不对称分量分解成对称的正、负序及同向的零序分量进行分析，变压器是电力系统中主要设备之一，因此变压器的零序电抗也是电力系统分析非常重要的参数之一。本文对心式电力变压器的零序电抗进行了分析，针对不同结构的变压器提出了详细的计算方法。

1 磁路与零序电抗

由于零序磁通与正序、负序磁通一样为交变分量，且存在相同的电磁感应关系，因此用于表示正序电磁关系的近似“Γ”型等效电路仍可用于零序（见图1），由图1可得变压器的零序电抗为

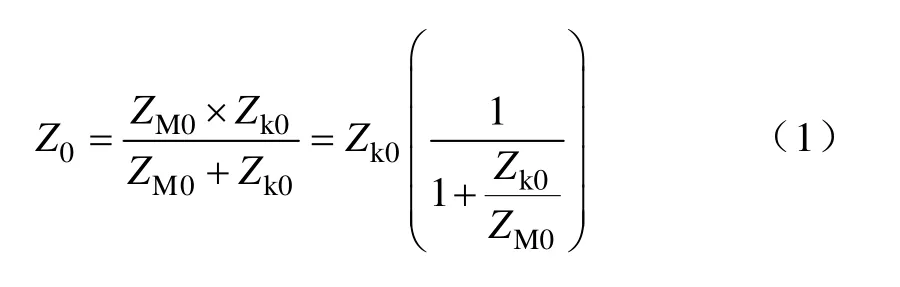
式中，ZM0为变压器的零序励磁电抗；ZK0为零序下的绕组漏电抗。

由于绕组漏电抗与相序无关，所以零序与正序时的绕组漏电抗基本相同，即 ZK0与变压器短路阻抗ZK基本相同。

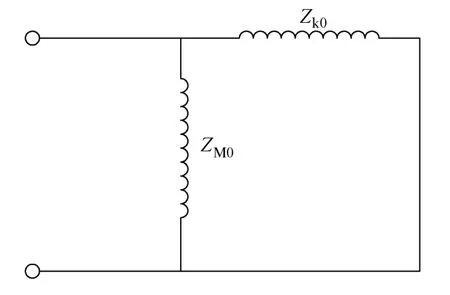
图1 变压器零序等效电路

ZM0与磁路系统有关，变压器磁路按铁心结构可分为带旁柱（如三相五柱式、单相三柱式）和不带旁柱（例如三相三柱式）的结构。带旁柱的铁心结构，零序磁通可以通过旁柱形成闭合回路，如图 2所示，零序励磁电抗很大，其远远大于绕组漏电抗，ZM0支路可以认为是开路，因此对于带旁柱的铁心变压器零序电抗近似等于变压器短路阻抗；对于不带旁柱的变压器，零序磁通只能通过空间和油箱等低导磁材料形成闭合回路，而空间的磁导率很低，这个回路磁阻很大，因此零序励磁电抗比带旁柱结构要小很多，此时ZM0支路不可忽略，由式（1）可知，变压器零序电抗比变压器短路阻抗小。

图2 三相五柱铁心零序磁路分布

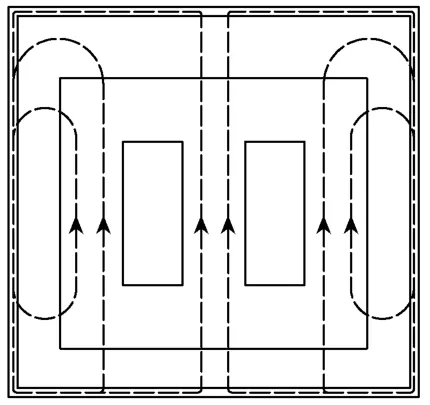
图3 三相三柱铁心零序磁路分布

2 联接组别与零序电抗

联接组别对于变压器的零序电抗有直接影响。按联接组别可分为：有三角形连接的零序电抗和无三角形连接的零序电抗，由于三相零序电流同向，所以对于含三角形连接组的变压器不论三角形连接侧是短路还是开路，零序电流均可在三角形连接的绕组内部流通，因此含三角形连接组的变压器仅有负载零序电抗；对于不含三角形联结组的变压器，当一侧加电，另一侧短路时，其零序电抗为负载零序电抗。当一侧加电，另一侧开路时，其零序电抗为空载零序电抗，此时的零序电抗等于零序励磁电抗。

对于三相五柱铁心或单相铁心，如果采用 Yy联接组别，则两侧中性点必须接地，因为有中性点接地的绕组中有零序电流，但在另一无中性点接地的绕组中无此电流，故零序电流不能安匝平衡，它会产生一个很大的零序电抗，相对地电压的对称会受到影响，中性点会有较大偏移，因此，不含三角形联结组的三相五柱铁心或单相组成的三相组铁心的变压器尽量不采用这种连接方式。

3 变压器型式与零序电抗

3.1 双绕组变压器

1）对于YD联结组的变压器，其零序电抗为Y侧绕组加电，另一侧绕组角接，

变压器零序电抗：

式中，Zk为变压器的正序短路电抗。

2）对于YY联结组的变压器，其零序电抗为：

一侧绕组加电，另一侧绕组短接，变压器零序电抗同式（2）。

一侧绕组加电，另一侧绕组开路，变压器零序电抗：

3.2 三绕组变压器

按变压器用途分为降压变和升压变，降压变绕组排列由内向外为低压绕组（d接）-中压绕组（y接）-高压绕组（Y接），升压变绕组排列由内向外为中压绕组（y接）-低压绕组（d接）-高压绕组（Y接）。

根据变压器的运行情况，三绕组变压器的零序电抗为：

1）高压加电，中压短路，低压角接

对于降压变，由于中压处于短路状态，低压绕组中没有零序电流，此时变压器零序电抗：

式中，ZkHM为变压器高-中正序短路电抗。

对于升压变，由于低压为角接（对于零序，相当于短路状态），中压绕组中没有零序电流，此时变压器零序电抗：

式中，ZkHL为变压器高-低正序短路电抗。

2）高压加电，中压开路，低压角接，不论是降压变还是升压变，变压器零序电抗计算公式同式（5）。

3）中压加电，高压短路，低压角接

对于降压变，这种工况时高压和低压中均有零序电流，变压器绕组中零序电流的分配与变压器联合运行时中压供电，高低压侧短路相同，其零序电抗：

此时等效电路如图4所示，图中ZkH、ZkM、ZkL分别为三绕组变压器中各绕组的等效阻抗。其值可由变压器的短路阻抗求出，计算公式见式（7）—式（9）：

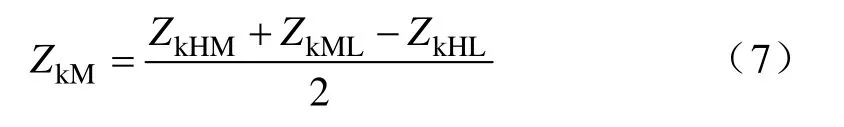
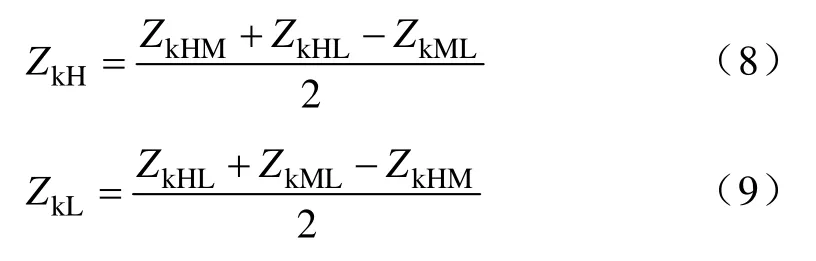
式中，ZkML为变压器中-低正序短路电抗。

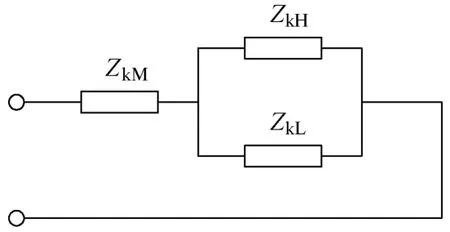
图4 降压变中压加电，高压短路，低压角接等效电路

总等效阻抗为：

对于升压变，由于低压处于角接状态，所以高压绕组中没有短路电流，其零序电抗：

4）中压加电，高压开路，低压角接，不论是降压变还是升压变，变压器零序电抗计算公式同式（11）

注：该节中修正系数K见表1，表中数据为笔者对大量产品的试验数据统计分析得到。

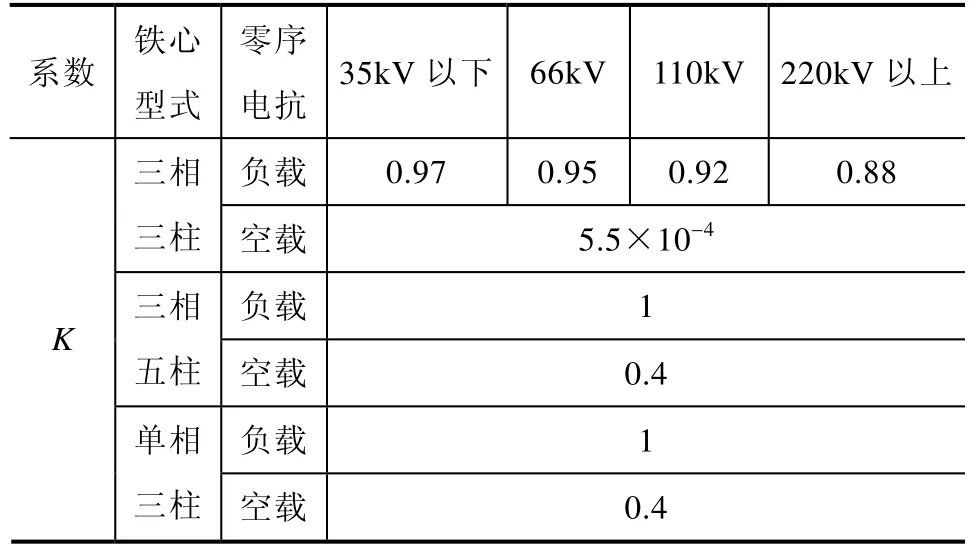
表1 零序电抗修正系数K

4 零序电抗的计算和仿真

4.1 双绕组变压器，联结组Yd

例如一台SF-35000/20变压器，联接组别Dyn1，铁心型式为三相三柱式，高压电压13.8kV，低压电压6.3kV，短路阻抗测量值13.2%（折算至低压侧欧姆值为 0.15Ω），由式（2）得零序电抗 Z0=0.97×0.15=0.146Ω，该产品零序电抗实测值为0.151Ω，与计算值偏差仅为-3.31%。表2为采用此方法计算的变压器零序电抗。

表2 变压器零序电抗计算值与测量值

由第二节分析可知，对于三相五柱式铁心，可以认为激磁回路是开路的，零序电抗仅与短路阻抗有关，因此利用短路阻抗计算零序电抗非常准确；而三相三柱式铁心的零序电抗不仅与短路阻抗有关，还与零序激磁电抗有关，零序激磁电抗又与变压器结构紧密相关，因此三相三柱式变压器零序电抗受变压器结构影响较大，上节表1中给出的三相三柱式铁心修正系数K仅供参考，如果想得到准确的三相三柱式铁心结构变压器零序电抗可采用仿真计算。

表2中SF-35000/20变压器采用仿真计算结果如图5至图7所示。

利用MAGNET基于有限元法的3D时谐场求解器，进行场路耦合分析，磁场计算实体模型如图 5所示，电路模型如图6所示。

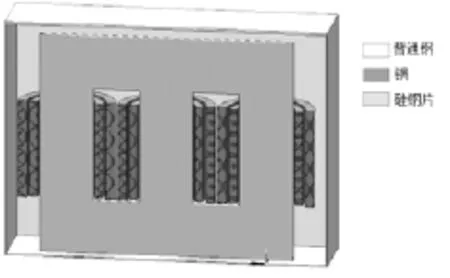
图5 实体模型

图6 电路模型

高压侧角接，在低压侧a、b、c三相施加10.31V（由于变压器的对称性，仅取 1/2模型进行仿真计算，此电压为 1/2模型上的电压，整个模型上电压为20.62V）同相位电压，磁场计算得到低压侧零序电流为 134.98A，见表 3，因此变压器零序阻抗Z0=20.62/134.98=0.152Ω，与试验值偏差为0.66%。

图7 有限元模型

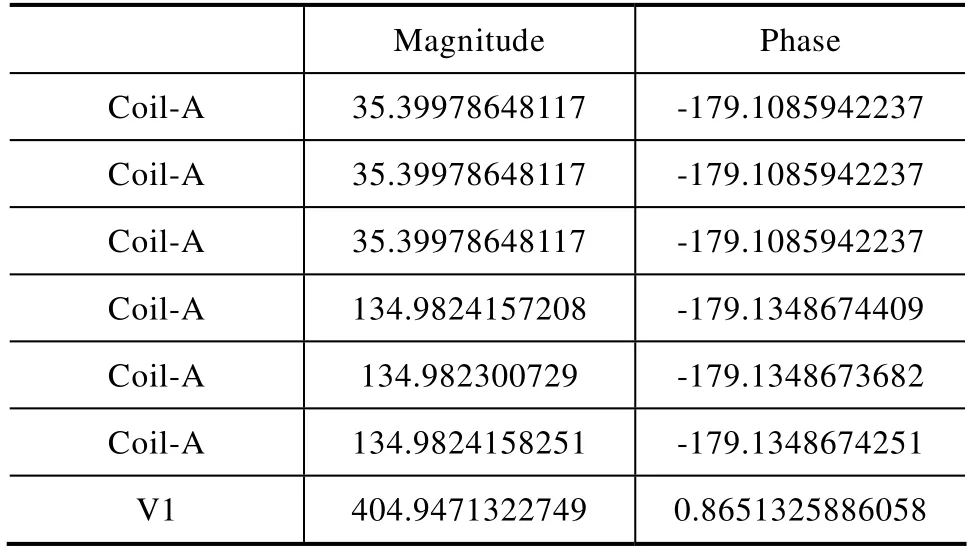
表3 各元件中的电流

图8为通过磁场计算得到的三相零序磁通矢量图，由图可以看出，三相零序磁通通过铁心、气隙、油箱闭合，与第二节的分析吻合。

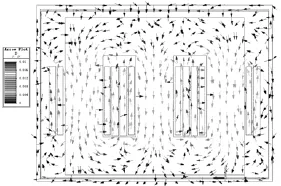
图8 零序磁通矢量图

4.2 双绕组变压器，联结组Yy

例如一台 SFZ-75000/220变压器，联接组别YNyn0，铁心型式为三相三柱式，高压电压220kV，低压电压13.8kV，短路阻抗测量值12.03%。

1）负载零序电抗计算

高压侧加电，低压侧短路，短路阻抗折算值高压侧欧姆值为 77.64 Ω，由式（2）得零序电抗 Z0= 0.88×77.64=68.32，该产品零序电抗实测值为69.4Ω，与测量值偏差-1.56%。

高压侧短路，低压侧加电，短路阻抗折算值低压侧欧姆值为 0.305Ω，由式（2）得零序电抗 Z0= 0.97×0.305=0.296，该产品零序电抗实测值为0.309Ω，与测量值偏差-4.21%。

2）空载零序电抗计算

该联结组铁心为三相三柱式变压器负载零序电抗亦存在零序电抗计算误差偏大的问题，原因同4.1节。

空载零序电抗不仅受变压器结构影响，还与加电绕组的位置，施加电压、铁心励磁特性等有关，因此工程计算方法无法准确计算空载零序电抗，由表4该变压器零序电抗测量结果可以看出，施加电压不同时，其空载零序电抗测量值变化非常大。

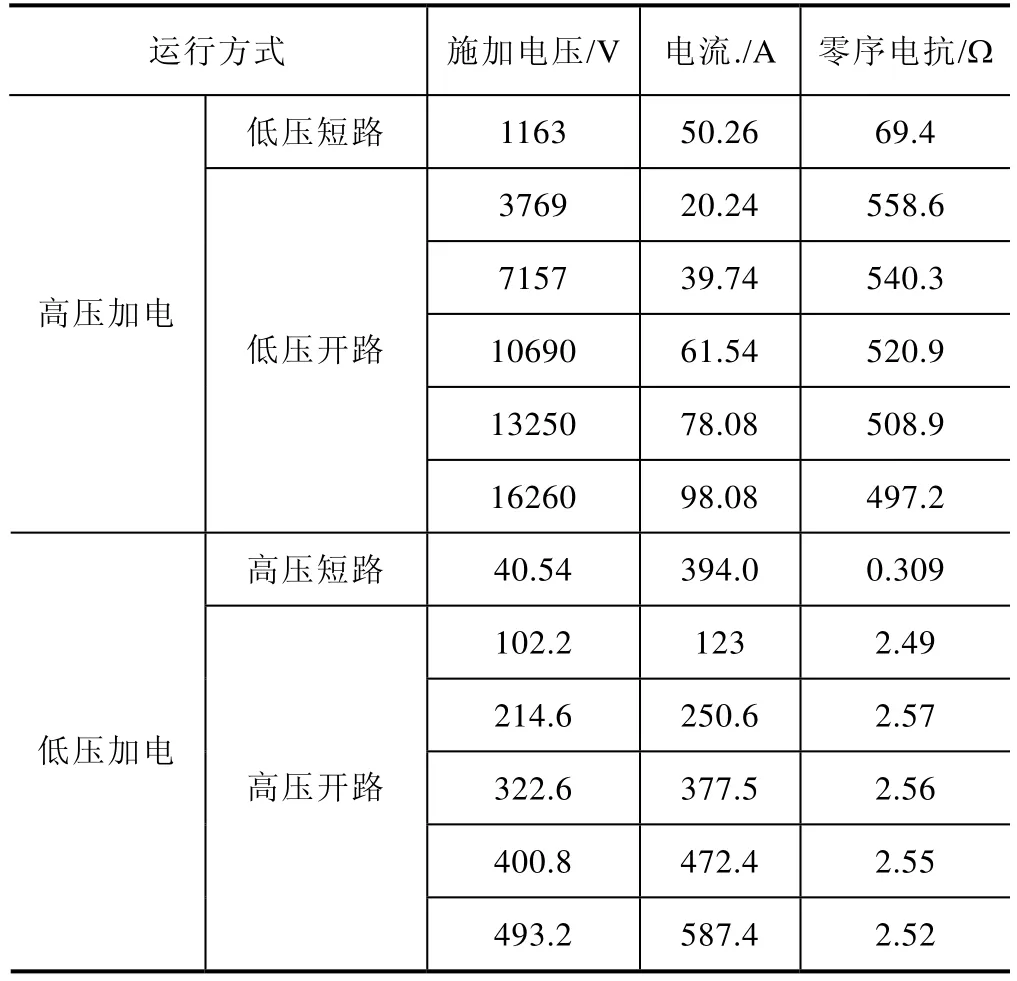
表4 变压器零序电抗测量值

4.3 三绕组变压器，联结组Yyd或Ya0d

如一台OSFSZ-180000/220自耦变压器，联接组别 YNa0d11，铁心型式为三相三柱式，高压电压220kV，中压电压115 kV，低压电压10.5kV，短路阻抗测量值：高-中 12.97%，中-低 46.45%，高-低63.33%。

1）高压加电，中压短路，低压角接

高中阻抗折算至高压侧欧姆值为 34.87，由式（4）得零序电抗 Z0=0.88×34.87=30.69Ω，实测值为 31.9Ω，与实测值偏差为-3.82%；仿真计算值为31.5%，与实测值偏差为-1.25%。

2）高压加电，中压开路，低压角接

高低阻抗折算至高压侧欧姆值为 170.28，由式（5）得零序电抗 Z0=0.88×170.28=149.85Ω，实测值为147Ω，与实测值偏差为1.94%；仿真计算值为146.5%，与实测值偏差为-0.34%。

3）中压加电，高压开路，低压角接

中低阻抗折算至中压侧欧姆值为 34.13，由式（11）得零序电抗Z0=0.92×34.13=31.40Ω，实测值为31.68Ω，与实测值偏差为-0.88%；仿真计算值为31.43%，与实测值偏差为-0.79%。

4）中压加电，高压短路，低压角接

由式（7）至式（10）得联合运行时变压器等值阻抗：

联合运行阻抗折算至中压侧欧姆值为 6.94Ω，由式（6）得零序电抗 Z0=0.92×6.94=6.38Ω，实测值为 6.59Ω，与实测值偏差为-3.19%；仿真计算值为6.47%，与实测值偏差为-1.82%。

受篇幅所限，本节中未列出详细的仿真计算过程，仿真计算的方法同4.1节，其仿真计算有限元模型如图9所示。

图9 仿真计算有限元模

5 结论

1）对于带旁柱的铁心，变压器负载零序电抗近似等于变压器短路阻抗，空载零序电抗约为正序励磁电抗的40%；对于不带旁柱的铁心，变压器负载零序电抗约为变压器短路阻抗90%，空载零序电抗约为正序励磁电抗的0.055%。

2）对于三相五柱式铁心或单相铁心的变压器零序电抗，利用公式可以精确计算；对于三相三柱式铁心，零序磁通需要通过气隙、油箱等闭合，不同变压器因其结构不同，修正系数K存在不确定性，但可以满足工程计算需要，如果想准确计算零序电抗，需采用磁场仿真计算。

3）对于Yy连接的变压器，空载零序电抗受变压器结构、铁心励磁特性、测量电压等因素的影响，无论采用公式法还是仿真均无法准确计算。

[1]李光琦.电力系统暂态分析[M].北京: 水利电力出版社, 1985.

[2]尹克宁.变压器设计原理[M].北京: 中国电力出版社, 2003.

[3]张国兵.三相五柱式变压器零序阻抗的分析和计算[J].变压器, 1995(10): 12-15.

[4]刘传彝.电力变压器设计计算方法与实践[M].沈阳:辽宁科学技术出版社, 2002.

Calculation and Simulation for Zero-sequence Reactance of Power Transformer

Liu Liqiang Wang Chungang
(Baoding Tianwei Baobian Electric Co., Ltd, Baoding, Hebei 071056)

This paper Discusses the relationship between the zero-sequence reactance and transformer magnetic circuit, connection groups, transformer structure and so on,and gives the calculation method of zero-sequence reactance for various kinds of transformer.

zero-sequence reactance; short circuit impedance; excitation impedance; magnetic circuit; connection groups

刘力强（1975-），男，河北藁城人，保定天威保变电气股份有限公司高级工程师，主要从事电力变压器设计研发工作。