多目标函数预抗差估计
李 骁 高宗和 龚成明 王 毅 邹德虎
(国家电网电力科学研究院,南京 211106)
多目标函数预抗差估计
李 骁 高宗和 龚成明 王 毅 邹德虎
(国家电网电力科学研究院,南京 211106)
对于电力系统中出现在杠杆量测上的不良数据,传统含不良数据辨识的最小二乘法状态估计不能很好排除不良数据对系统估计结果的影响。本文提出了多目标函数预抗差状态估计,利用可变窗宽算法平衡了指数目标函数状态估计的精度与速度矛盾,同时利用加权最小二乘估计与之相结合,在不同的迭代周期中使用不同的目标函数,使得估计既可以具有结构抗差估计的优秀抗差性能,又使得估计具有最小二乘法相对优秀的收敛性,避免了迭代震荡浪费计算资源的情况。将本文所提方法与传统算法进行比较,结果表明本文所提出的算法在性能上具有明显优势。
电力系统;状态估计;多目标函数预抗差;迭代变权法;抗差估计
电力系统状态估计利用实时量测系统的冗余度来提高数据精度,自动排除随机干扰所引起的错误信息,估计或预报系统的运行状态[1-2]。其计算性能和精度直接决定高级应用软件的计算可靠性。
具有不良数据辨识环节的加权最小二乘估计(residual-neutralized weighted least square,RnWLS)是目前状态估计中应用最为广泛的主流方法,优点是模型简单,计算量小,对理想的正态分布的量测量,估计具有最优性且无偏等优良统计特性。基于M估计的抗差估计具有一定的抗差性,在估计过程中可以无需额外计算自动排除不良数据;但是其无法有效应对不良杠杆量测对估计结果的负面影响[3-6]。为了解决这一问题,文献[7-9]提出了指数型目标函数抗差估计方法,由于量测残差灵敏度矩阵的对角元在残差较大时均不为零,因此具有良好的结构抗差性能,但其估计精度和收敛性取决于窗宽参数,并且相互矛盾,在高精度要求下可能出现迭代震荡的情况。
本文提出了多目标函数预抗差(multi objective function pre-treatment,MOFP)状态估计方法,应用自适应可变窗宽的指数目标函数状态估计和多目标函数预抗差估计,在不同的迭代周期中使用不同的目标函数,使得估计既可以具有结构抗差估计的优秀抗差性能,又使得估计具有最小二乘法相对优秀的收敛性,避免了迭代震荡浪费计算资源的情况。
1 可变窗宽指数型目标函数状态估计
指数型目标函数(maximum exponential square,MES)电力系统抗差估计的模型可以表示为[7]
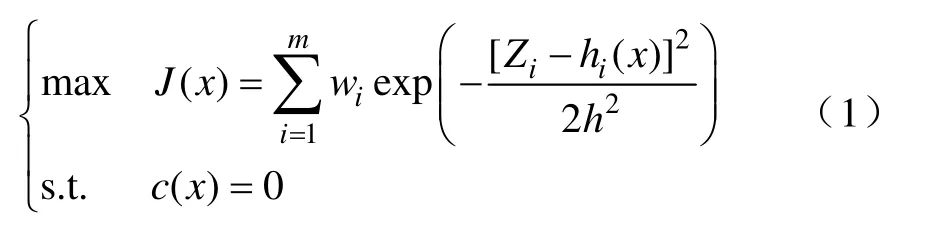
式中,x为系统状态变量;wi为量测权重,m为量测数,为量测函数,即用状态变量计算出的量测值,Zi为量测的量测值;h为模型中暂未给出的窗宽。由于其残差灵敏度矩阵在残差较大时不为0,对于杠杆量测中出现的不良数据具有较好的抵抗能力[7-10]。
指数目标函数状态估计中,窗宽的选择直接关系到整个估计的计算速度与精度。当窗宽选择较大时,目标函数较为平缓,收敛速度慢,结果精度也较低,但是不容易出现局部最优解;当窗宽选择较小时,目标函数较为尖锐,在每个波峰附近收敛速度明显较快,但是在较小的峰处容易陷入局部最优解。因此对于估计而言,估计的迭代收敛速度和估计的结果精度、迭代收敛性这两方面是相互矛盾的。
为解决这一窗宽选择问题,使用均方误差(mean squraerd error,MSE)或风险(risk)来衡量估计的性能[11-14]。其计算公式如下:
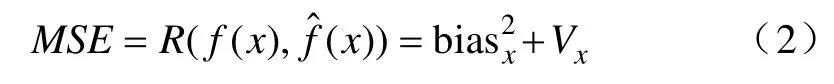
对风险作关于h的微分,并且在其为0时,对于我们选定的高斯核函数,若假设真实分布光滑[18],则可以计算出:

使用每步迭代才残差 r的均方根来近似样本标准差:

由于在多目标函数预抗差中,指数目标函数估计主要作为初期预抗差环节,并考虑迭代近似时的误差所需的余量,在迭代过程中,在h*后面乘以一个大于1的关于迭代次数it的渐减修正函数以保证迭代的最初阶段不会落入局部最优点附近:

2 基于指数目标函数的多目标函数预抗差估计
可变窗宽指数型目标函数状态估计尽管在一定程度上解决了指数目标函数窗宽选择困难的问题,但是在计算中仍然在少数情况,比如所有量测都极为准确而残差极小的状态下出现迭代震荡而无法收敛的情况。但是经过对数据的研究,常见发现开始迭代震荡时经过的迭代次数并不多,杠杆量测上的不良数据已经得到消除,而仅仅在少数数值处发生小幅度震荡。此时继续进行同样的迭代不仅仅浪费计算资源,而且也无法获得更加精确的结果。
多目标函数预抗差算法基于迭代变权法,将最小二乘估计和可变窗宽指数状态估计相结合,以期待获得良好抗差性能的同时,简化计算步骤,避免迭代震荡。其估计过程中通过迭代变权法,在不同的迭代周期中使用不同的目标函数,从而获得多种状态估计目标函数具有的优点并回避其可能的缺点。首先通过可变窗宽指数目标函数状态估计来消除包括杠杆量测上的不良残差,并使用加权最小二乘法来保证迭代的收敛性。其基本算法为:
1)在初次迭代时,采用普通最小二乘状态估计,获得可变窗宽指数型目标函数估计求取窗宽所需的残差量。
2)随后以可变窗宽指数型目标函数状态估计进行至多4次的抗差估计迭代,排除包括杠杆量测上的不良数据。
3)若可变窗宽指数型目标函数状态估计迭代过程中收敛,则终止迭代,否则进行最大标准化残差检测并消除残差,继续使用最小二乘状态估计迭代至收敛。
由于在迭代变权法中,可变窗宽指数型目标函数状态估计与加权最小二乘状态估计目标函数的差异反映在权重计算环节,因此仅需要在权重计算环节判定迭代次数从而更改权重计算公式,实现较为方便。算法流程图如图1所示。

图1 MOFP状态估计算法流程图
3 算例分析
为了评估本文所提出的多目标函数预抗差估计的性能,对于以IEEE-30和IEEE-118标准节点为基础搭建的完全量测测试系统进行测试,并使用江苏电网1098节点系统断面数据进行验证。每个量测使用潮流计算真值加上量测误差来模拟。量测误差em可以表示为如下形式:

式中,Vt是量测值真值;Vf是满刻度值;am是与量测值有关的误差系数;bm是与满刻度值有关的误差系数,N(0,1)为符合标准正态分布函数的白噪声。
对基于IEEE-30的模拟系统,对于所有量测均在精准值上增加误差1em的误差模拟正常量测误差,在显示出强杠杆性的 27-28节点线路末端有功量测上增加15em的极大误差来模拟不良数据,验证算法在多不良数据下的性能。其不良杠杆量测的状态估计结果见表1。WLS算法的误差为量测值的123%,而多目标函数预抗差估计对此此量测估计误差仅仅为21%,可以认为多目标函数预抗差估计对于杠杆量测上不良数据的具有远超 WLS的较强的抵御效果,显示出了非常好的性能。

表1 WLS状态估计和MOFP状态估计对IEEE-30节点系统不良数据的估计结果比较
对于基于IEEE-118节点,量测数达到1098个的模拟系统,对于所有量测均在精准值上增加误差1em的误差模拟正常量测误差,在杠杆性较强的183支路末端无功潮流量测上增加15em的明显误差。其对比数据任然显示出多目标函数预抗差估计在较多节点数据下的同样有较好抗差能力。
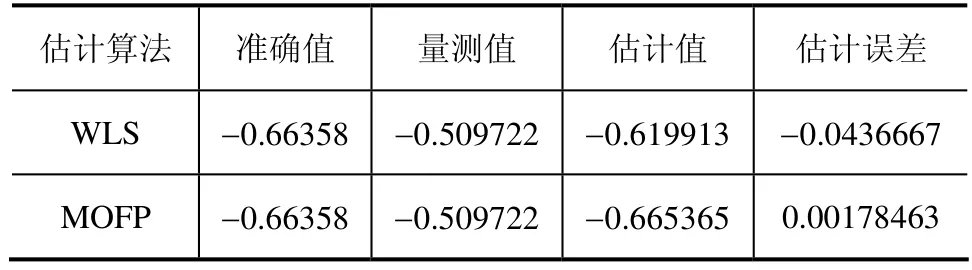
表2 WLS状态估计和MOFP状态估计对IEEE-118节点系统不良数据的估计结果比较
RnWLS和MOFP估计在算例中的总体评价指标见表 3。MOFP估计算法的电压幅值偏离距离、电压相角偏离距离、最大标准化误差、误差目标函数、误差均方根值这四项状态估计评估指标 MOFP均比 RnWLS有明显的领先,计算时间则由于迭代次数略高于 WLS估计,但仍然在可以接受的范围内。
对于一个总体量测十分精确的系统,仅仅采用变窗宽指数目标函数状态估计时,因窗宽依赖于残差同样较小,易发生在精确结果附近震荡的情况。而多目标函数预抗差估计则能够避免这样的收敛性问题。以江苏电网1098节点系统为例,对于所有量测均在精准值上增加误差 0.1em的误差模拟量测精确的情况,并在三号线路首端有功潮流量测上增加15em的不良数据误差。由于此量测并非杠杆量测,RnWLS算法在此算例上表现符合预期。单纯的可变窗宽指数目标函数估计法此时迭代次数较多,消耗大量的时间,而多目标函数预抗差估计则在保证迭代精度的情况下完成了快速收敛,节约了大量时间。
以上算例表明MOFP不仅仅具有较高的抗差性能,同时其额外计算量控制较好,具有工程实用性。

表3 WLS和MOFP状态估计对IEEE-30和118节点系统的估计结果比较

表4 RnWLS、MES和MOFP状态估计对JS-1098节点系统的估计结果比较
4 结论
本文提出了多目标函数预抗差状态估计方法,首先使用可变窗宽算法改进指数目标函数状态估计,使之能够自适应系统,额外计算量小,同时能够有效排除各类不良数据对系统估计结果的影响;同时又结合了传统的加权最小二乘法易收敛,计算量相对较小的特点,避免了各类指数目标函数状态估计都容易出现的收敛性问题,使得状态估计程序整体能在可以接受的时间内得出较为准确的估计结果,避免了之前多种状态估计算法难以在估计时间与估计精度中做出平衡的问题,算例分析也证明了此算法具有进一步发展与进行工程实践的空间。
[1]于尔铿.电力系统状态估计[M].北京: 水利电力出版社, 1985: 1-8.
[2]诸骏伟.电力系统分析[M].北京: 中国电力出版社, 1995: 74-84.
[3]相年德, 王世缨, 于尔铿.电力系统状态估计中的不良数据估计识别法(第一部分):理论与方法[J].电力技术通讯, 1979, 19(8): 1-27.
[4]Monticelli A.Multiple bad data identification for state estimation by combinatorial optimization[J].IEEE Trans.on Power Delivery, 1986, PWRD-1(3): 361-369.
[5]赵海天, 相年德, 王世缨, 等.多不良数据的相关量测检测方法[J].中国电机工程学报, 1990, 10(6): 26-32.
[6]亓俊健, 何光宇, 梅生伟, 等.电力系统抗差状态估计研究综述[J].电工电能新技术, 2011, 30(3): 59-64.
[7]吴文传, 郭烨, 张伯明.指数型目标函数电力系统抗差状态估计[J].中国电机工程学报, 2011, 31(4): 67-71.
[8]郭烨, 张伯明, 吴文传.指数型目标函数电力系统抗差状态估计的解法与性能分析[J].中国电机工程学报, 2011, 31(7): 89-95.
[9]姚诸香, 郭烨, 郭玉金, 等.含指数型目标函数的电力系统抗差状态估计方法在江西电网中的应用[J].电网技术, 2012, 36(4): 155-159.
[10]付艳兰, 陈艳波, 姚锐, 等.基于最大指数绝对值目标函数的抗差状态估计方法[J].电网技术, 2013, 37(11): 3166-3171.
[11]David W S.On optimal and Data-Based histograms[J].Biometrika, 1979, 66(3): 605-610.
[12]Chen Badong, Xing Lei, Zhao Haiquan, et al.Generalized Correntropy for Robust Adaptive Filtering[J].Eprint Arxiv, 2015
[13]Liu Weifeng, Pokharel P P, Principe J C.Correntropy: properties and applications in Non-Gaussian signal processing[J].IEEE Transactions on Signal Processing, 2007, 55(11): 5286-5297.
[14]Han Seungju, Rao Sudhir, Deniz, et al.An improved minimum error entropy criterion with self adjusting step-size[C].IEEE Workshop on Machine Learning for Signal Processing, 2005.
[15]Bernard Silverman.Density estimation for statistics and data analysis[M].1986.
[16]Larry Wasserman.All of nonparametric statistics[M].2006, 125-130.
[17]何晓群.多元统计分析[M].北京: 中国人民大学出版社, 2004.
[18]盛骤, 谢式千, 潘承毅.概率论与数理统计[M].北京: 高等教育出版社, 2008.
Multi Objective Function Pre-treatment Robust State Estimation
Li Xiao Gao Zonghe Gong Chengming Wang Yi Zou Dehu
(State Grid Electric Power Research Institute, Nanjing 211106)
Traditional weighted least square state estimation method with bad data identification progress cannot eliminate the influence of bad leverage data on the result of estimation.The multi objective function pre-treatment robust state estimation was proposed.This estimation use variable window wide algorithm choose the best parameter for maximum exponential square object function , and combined weighted least square estimation to get advantages of both estimator.It was robust and had good convergence.The result of estimation of test systems proved the proposed algorithm have obvious better performance.
power system; state estimation; multi objective function pre-treatment; variable weight iterate; robust estimation
李 骁(1990-),男,国家电网电力科学研究院在读硕士研究生,研究方向为电力系状态估计。

