基于MLD的微电网多逆变器并联组态的建模及优化控制
周东来,龚仁喜,彭立亮,刘 畅
(广西大学电气工程学院, 广西南宁530004)
基于MLD的微电网多逆变器并联组态的建模及优化控制
周东来,龚仁喜,彭立亮,刘 畅
(广西大学电气工程学院, 广西南宁530004)
针对现有微网逆变器并联系统建模精度不高、控制方案复杂、控制效果不理想等问题,文中提出了一种基于混合逻辑动态(MLD)的光伏微网多并联逆变器的建模和优化控制方法。该方法将每个开关周期分为多个子周期,同时引入逻辑变量来判断系统运行的动态模式;然后用HYSDEL工具编程得到MLD模型;最后根据系统的自然约束及系统控制目标设计预测控制器,并通过求解相应的整数线性规划问题达到减少输出电压跟踪误差及各逆变器之间的环流的目标。相较传统的建模与控制方法,该方法具有模型精度高、控制方案简便、控制效果好的特点。仿真结果验证了模型的正确性和控制器性能的优越性。
微电网;并联逆变器;混合逻辑动态建模;模型预测控制
随着全球能源问题的日益严峻以及用户对用电可靠性及安全性要求的日益提高,分布式发电系统应运而生。目前,大多数分布式电源通过逆变器接入电网,采用适当的多逆变器并联技术,不仅可以突破地域限制将相距较远的不同分布式电源并联起来提高发电系统的容量,同时也可组建并联冗余系统提高发电系统运行的可靠性。
针对逆变器的建模,目前普遍采用周期平均的方法,该方法在一个采样周期内对系统状态进行平均,将实际的混杂系统近似为线性系统进行处理,忽略功率器件的开关特性[1],导致模型精度不高,会影响基于模型设计的控制器的性能。
针对逆变器并联运行系统控制,常用的方法有频率电压下垂控制法和PQ下垂控制法,这两种方法都是通过对电压跟踪以及均流这两个控制目标的相互制约来实现各逆变器之间的功率平衡[2];前者的缺点是瞬态响应速度较慢,后者可有效提高瞬时响应速度,但总的说来对多目标的控制效果都不理想[3-4]。为了提高多目标控制效果,人们提出了多种瞬时均流控制方法,如主从均流控制法[5-6]、循环链均流控制法[7]、平均均流控制法[8-9]。与下垂控制法相比,这些方法的优点是既可获得良好的电压跟踪效果,又可保证逆变器之间良好的瞬态均流,缺点是由于增加了逆变器之间额外的互联而造成控制器运行不稳定。
总的来说,这些建模及控制方法均没有考虑逆变器的混杂特性,因而都不能较好地反映这类系统的本质。为此,本文提出了一种基于混合逻辑动态(Mixed Logic Dynamic,MLD)的微网多并联逆变器建模和预测控制方法。在建模过程中通过引入辅助逻辑变量和连续变量,将系统所受到的逻辑约束、控制规则、离散及连续特性集成在一个统一的模型框架下,建立起系统的状态方程——带有混合整数不等式约束的线性状态方程[11];然后使用MPT(Multi-Parametric Toolbox)工具箱将方程转化为混合整数规划问题,通过求解该问题得到闭环控制系统的控制输入;最后基于该模型,采用模型预测控制方法,实现了对系统的优化控制。
1 DC/AC并联运行系统MLD建模
1.1 MLD建模定义
MLD建模方法是将控制系统中的逻辑关系和约束关系用不等式来表示,并将该约束与表述状态演变的差分方程组合起来对混杂系统进行描述,即:
x(k+1)=Ax(k)+B1u(k)+B2δ(k)+B3z(k),
(1-1)
y(k)=Cx(k)+D1u(k)+D2δ(k)+D3z(k),
(1-2)
E2δ(k)+E3z(k)≤E4x(k)+E1u(k)+E5,
(1-3)
其中,x、u、y分别为混杂系统的状态、控制输入和输出,它们均包含连续和离散两部分;δ∈{0,1}和z分别表示引入的辅助逻辑变量和辅助连续变量。针对系统运行的自然特性限制以及为了系统安全稳定运行而加入的系统状态、输入、输出及其他变量的约束条件,则在建模过程中转化为不等式(1-3)[12]。
1.2 逆变器并联电路的状态空间模型
本研究中多分布式电源并联逆变器运行系统的电源种类包括光伏板和风机,这两种电源所具有的互补特性能够提高发电系统运行的效率及稳定性[13],其拓扑如图1所示。
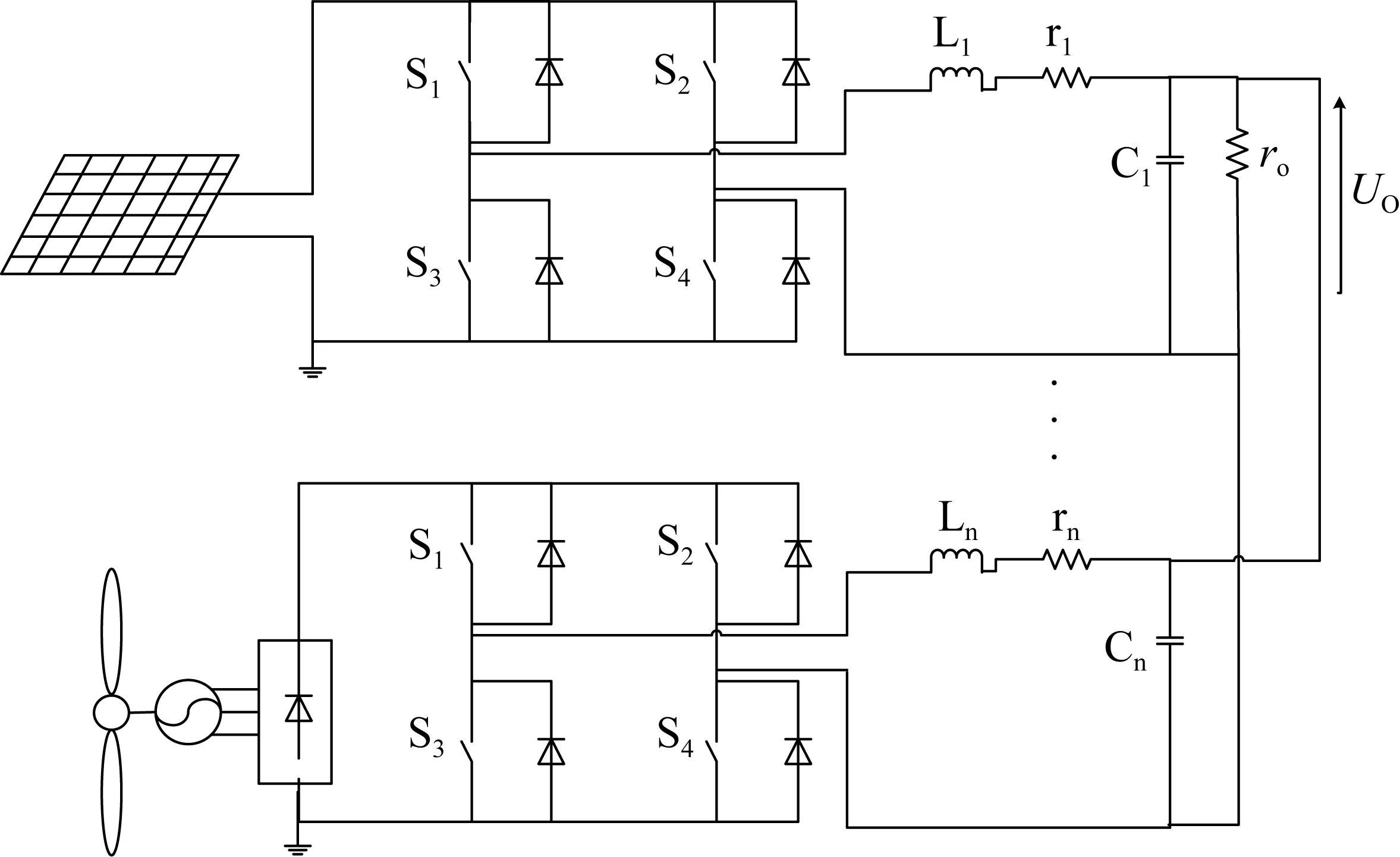
图1 逆变器并联运行系统结构
图1中,rn为电感的等效串联电阻,Ln、Cn分别表示各逆变单元的滤波电感电容。针对系统的控制目标,定义系统状态变量为X(t)=[UO,i1,i2,…,in]T,其中,i1,i2, …,in为流经各逆变器单元滤波电感的电流,UO是整个逆变器并联组态的输出电压。这里用Sn(t)代表第n个逆变器中功率开关管的开关状态,即:
(2)
式中,Sn1,Sn2,Sn3,Sn4分别代表系统中第n个逆变器的4个功率开关。为简化控制方案分析过程,设各并联逆变器直流侧输入电压均为US,系统的控制输入d(t)=(tn)/(TS)=[d1(t),d2(t),…,dn(t)],表示系统中各逆变器PWM控制波形的占空比。
由基尔霍夫定律,可得:
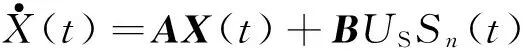
(3)
其中

(4)
将式(3)基于US归一化,状态量转换为x(t)=X(t)/US=[uo(t),il1(t),il2(t),…,iln(t)]T,得到如下表达式:

(5)
通过归一化,所建立的预测控制模型得以去除US的影响,从而可以简化控制器的设计。
1.3 离散混杂建模
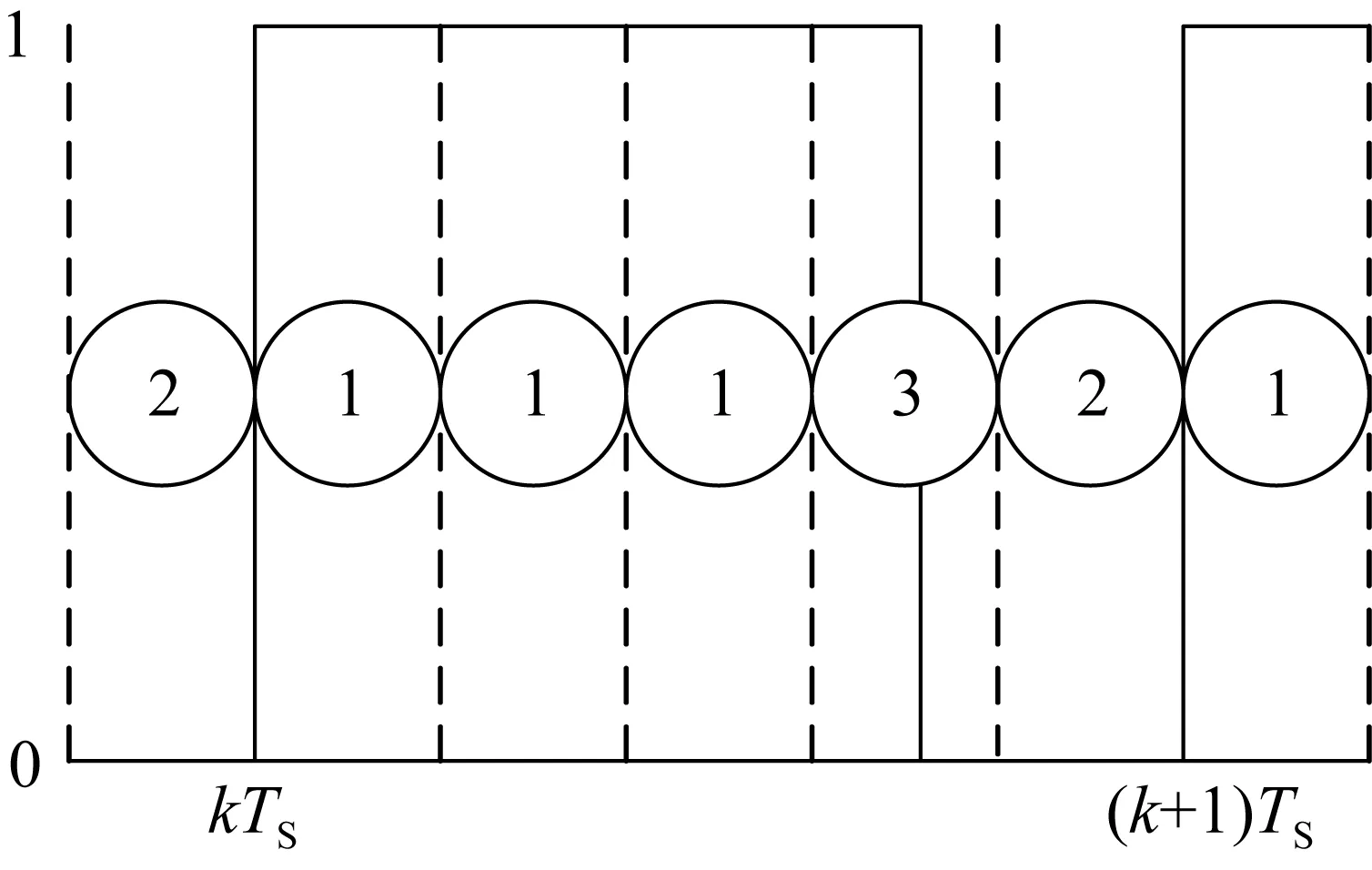
图2 开关周期划分Fig.2 Division of PWM period
为了方便描述并给出离散时间输入变量的变化,引入N步建模方法[14]对离散时间模型进行分析。
将开关周期TS分成N个长度为τs=TS/N(N≥1)的子周期,如图2所示。在子周期k,用ξ(m)表示时刻kTS+m·τS时的状态,其中,m∈{0,1,…,N},ξ(0)=x(k),ξ(N)=x(k+1),得到针对第m+1个子周期的离散模型:
ξ(m+1)=Φξ(m)+ΨB1+ΨB2+…+ΨBn。
(6)
因开关管所处状态的不同,ΨBn分别有以下3种模式:
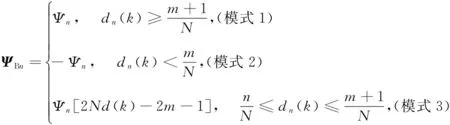
(7)
这里Φ和Ψ分别代表式(4)中描述的A和B在开关子周期时间τs下的离散形式,即:
Φ=eAτs,
(8)
Ψ=[Ψ1,Ψ2,…,Ψn]=-A-1(I-eAτs)B,
(9)
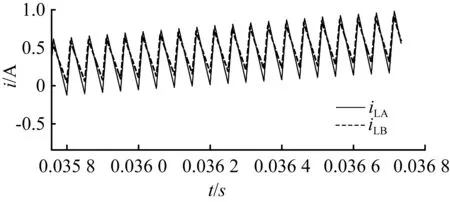
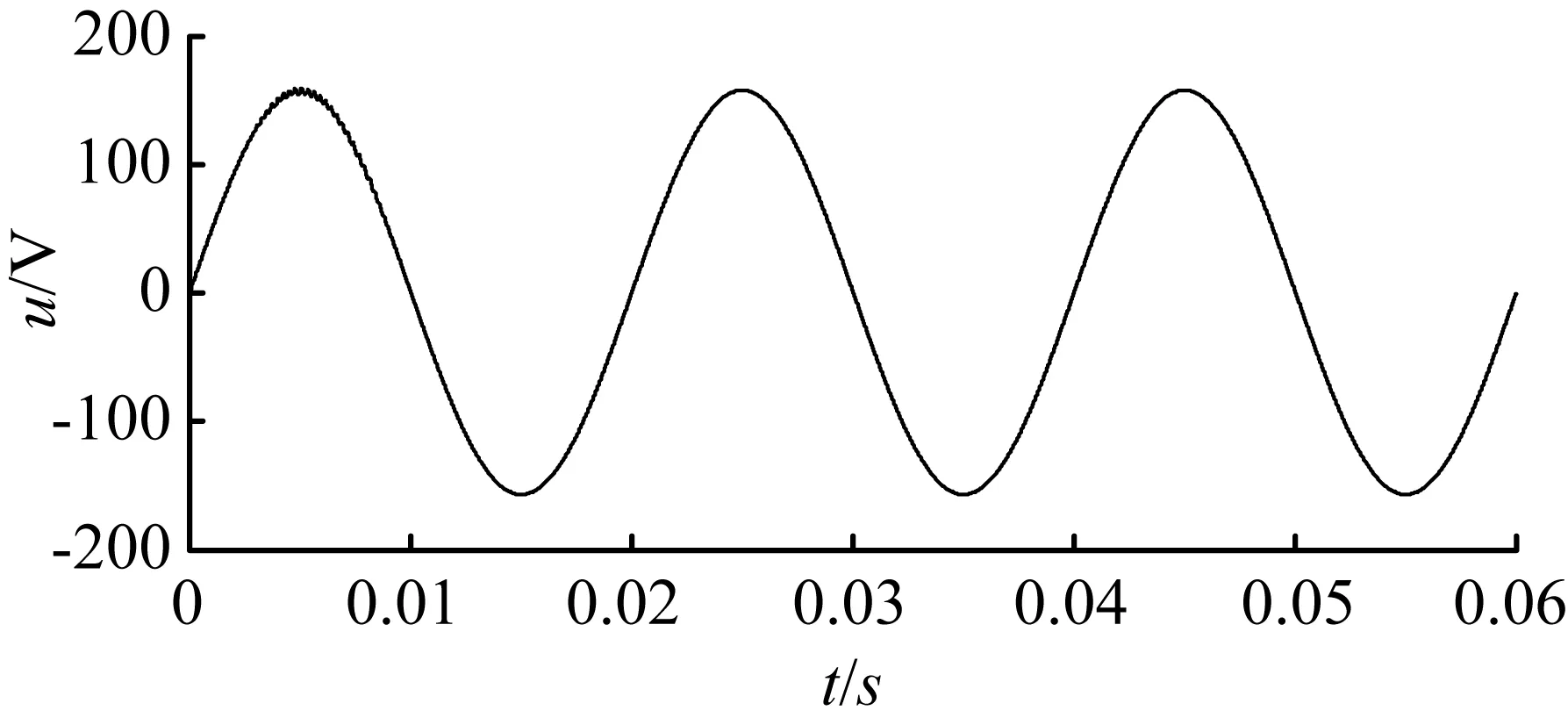
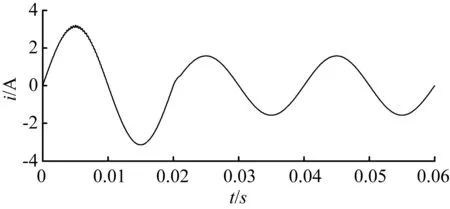
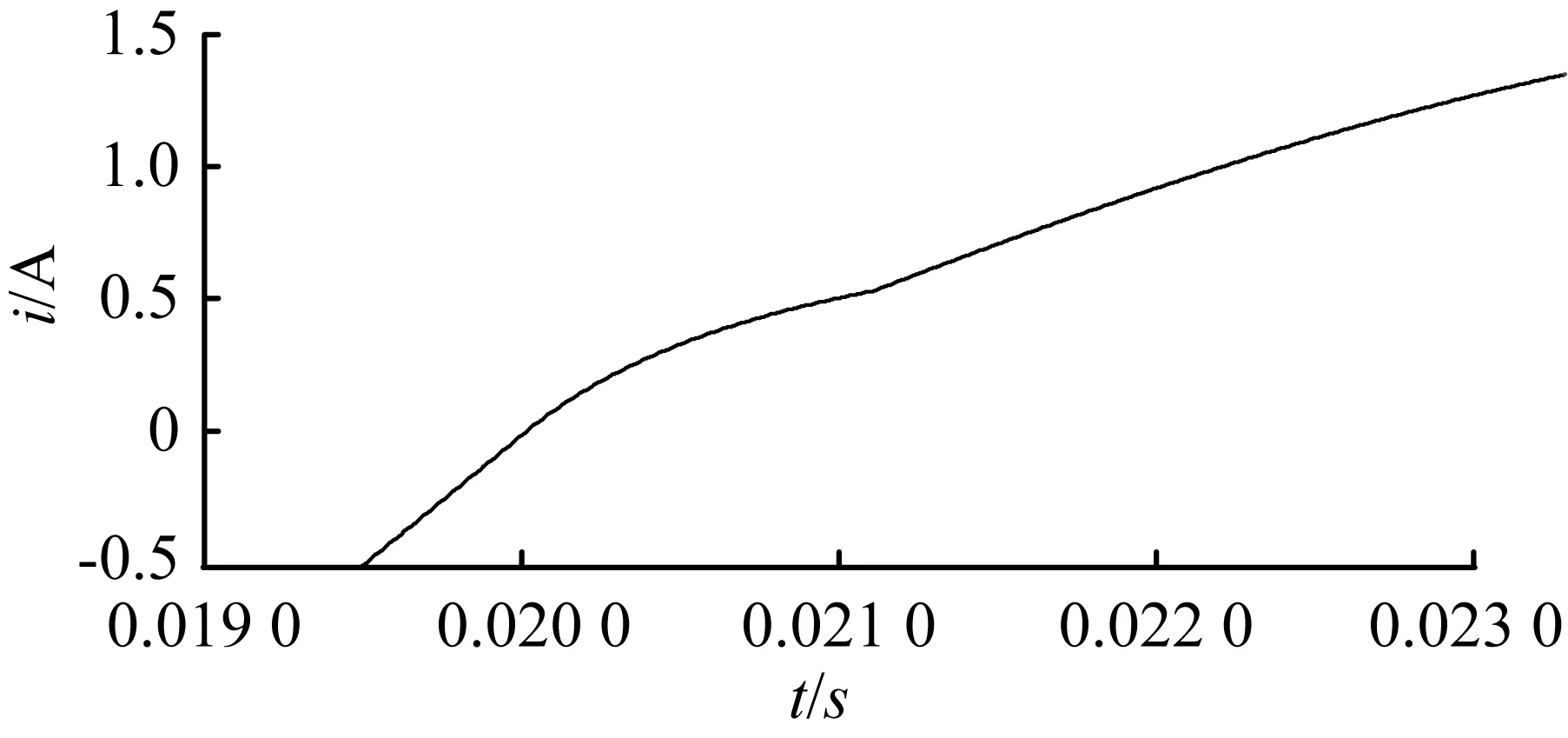
这里通过引入逻辑变量σn_m来判断子周期内的状态,针对系统中任一逆变器n的第m个子周期,如果σn_m=1,即说明d≥m/N,则逆变并联电路运行状态为模式1;如果σn_m=0,即说明d N步建模法相对精确地描述了系统在一个周期内状态的演变。对模型的近似处理只出现在功率管开关变化的子周期内。状态空间平均法对开关周期内状态的处理可以看做是N步划分中N=1这种特殊情况。N值选取得越大,状态变化时刻所处子周期所占比例越小,可有效降低误差,但同时会增加模型的复杂程度。本文采用HYSDEL语言编程,生成MLD模型,大大降低了建模的复杂度,简化了建模过程。 对于逆变器并联运行系统,控制的目标是实现输出电压快速稳定到设定目标值,同时使每个逆变器能够均匀地向负载供以电流,即逆变器间的环流最小。设计控制器的控制目标为调节平均输出电压能迅速准确地跟踪其参考值,每个逆变器能够尽量均分负载,使环流尽量小。 为此,首先需要确立控制目标函数,并根据目标函数获取优化状态反馈控制率,使目标函数在满足约束条件的情况下尽量小。 2.1 约束条件 根据电感电流的安全限值及功率开关管的物理性质,可引入约束条件: -il,max≤iln≤il,max, (10) 0≤dn(k)≤1。 (11) 2.2 目标函数 在第k个开关周期内,输出电压误差积分为: (12) 其中,uo,ref=UO,ref/VS,电流限制为il,max=IL,max/US;根据MLD建模方法,可将该误差积分近似表示为: (13) 在并联控制中必须保证每个逆变器均匀地向负载能够供以电流,理想中每个逆变器的输出电流为i*=il-ic,这里设ic≈C·[duo,ref(k)/dt],由此可引入均流误差: (14) 则第k个开关周期中的电流误差积分可表示为: (15) 式中,il,ref为均流误差的参考值,由均流控制目标可知该值设为0。 为表述方便,定义权值矩阵为Q=diag(q1,q2),其中,q1,q2∈R+。同时,将测量状态x(k),向量ε(k)=[uo,err(k)il,err(k)]T以及il,max(k)合并为一个状态向量p(k)=[(x(k))T, (ε(k))T, il,max]T,则目标函数表示为: (16) 式(16)中,ε(k+l|k)是在k个采样周期中第l步时的预测值,L为预测控制步长。计算t时刻MILP(混合整数预测)问题并求解,即得到一个最优控制序列: (17) 这里只将第一个控制信号dt*(0)输入系统进行控制,根据滚动优化的特点,反复求解该MILP问题,即可实现对系统的优化控制。在Matlab/Simulink中,使用MPT工具箱对控制参数进行设计,并计算求解,即得到闭环控制系统控制律。 为验证方法的有效性,利用Matlab/Simulink搭建了在统一框架下的两逆变器并联运行系统仿真模型。系统构成:2台逆变器采用电压型全桥电路,直流侧电压设为300 V,输出频率为50 Hz,峰值为155.6 V的正弦电压。主要参数:滤波电容Cf1=24 μF,Cf2=26 μF;滤波电感Lf1=6.8 mH,Lf2=5.9 mH;电感寄生电阻r1=0.56 Ω,r2=0.6 Ω;开关管开关频率fs=20 kHz。MLD建模N=2,预测控制步长为3。 图3示出了在相同标准负载及电路参数下,基于MLD法和状态空间平均法两种建模方法对系统进行建模并控制时的输出电压波形。图3(a)所示是基于MLD建模法且预测控制权值系数分别取q1=5,q2=1时系统输出电压跟综设定参考值的波形;图3(c)所示是基于状态空间平均模型的系统输出电压波形跟踪效果。对图3(a)和图3(c)的波形进行比较,可见图3(c)中输出电压波形在波峰以及波谷处的纹波比图3(a)所示波形的纹波大。图3(b)和图3(d)所示分别为图3(a)和图3(c)中跟踪效果的局部放大波形,以对基于两种方法的系统输出电压跟踪效果进一步进行对比。由图(3)中对比波形可以得出,相比状态空间平均建模法,基于MLD建模方法所设计的控制方案能够对输出电压进行更好的跟踪。 (a) 基于MLD模型的系统输出电压跟踪效果 (b) 基于MLD模型的系统输出电压局部波形 (c) 基于状态空间平均模型的系统输出电压跟踪效果 (d) 基于状态空间平均模型的系统输出电压局部波形 图3 系统在恒定负载50 Ω时输出电压跟踪波形 Fig.3 Output voltage tracking waveform for constant load of 50 Ω 图4示出了在标准负载及相应电路参数下系统的均流控制效果,基于MLD模型设计的预测控制算法中权值系数选取为q1=5,q2=1。从图4(a)中可得,基于MLD模型设计的闭环控制系统系统在初始阶段一直寻找最优控制序列,直到PWM波占空比序列在0.01 s后达到稳态,这从侧面反映均流控制效果良好。图4(b)及图4(c)所示分别是基于MLD模型的逆变并联运行系统中两个逆变单元A和B的滤波电感电流控制波形,在0.01 s之后,电感电流达到稳态。图4(d)是基于MLD模型的系统均流效果波形图,对比图4(e)中基于状态空间平均模型的系统均流控制效果,可见图4(d)中两路波形纹波小,重合度高,均流控制效果更好。通过将图4(d)波形进行局部放大得到图4(f)中系统达到稳态之后的两路电感电流局部波形对比图,可以看出,两路电感之间的误差始终控制在一个合理范围内。 图5示出了在t=0.02 s时负载由50 Ω突变到100 Ω时的仿真结果。由图5(a)及图5(b)可以看出,输出电压在负载突变时能准确地跟踪参考值,而负载电流在负载突变后随着新的负载的变化而处于另一稳态。由图5(c)可以看出,在0.02 s突变时刻开始,到0.021 0~0.021 5 s负载电流重新达到稳态,动态响应效果良好。 以上仿真结果证明了本文提出的建模以及控制方法的有效性。 (a) 基于MLD模型的系统控制PWM波占空比序列 (b) 基于MLD模型的逆变单元A滤波电感电流 (c) 基于MLD模型的逆变单元B滤波电感电流 (d) 基于MLD模型的系统均流控制效果 (e) 基于状态空间平均模型的系统均流控制效果 (f) 基于MLD模型的系统均流效果局部波形 图4 系统在恒定负载50 Ω时的均流控制效果 Fig.4 Current-sharing control effect for constant load of 50 Ω (a) 负载突变时输出电压波形 (b) 负载突变时负载电流波形 (c) 负载突变瞬间负载电流局部波形 本文基于MLD建模理论,对光伏微电网多逆变器并联组态进行了建模及控制方案设计。首先使用MLD模型分析了其混杂特性,然后基于MLD模型设计了优化控制方案,最后对方案进行了仿真。仿真结果表明,系统能使输出电压快速跟踪设定目标值,同时逆变器间的环流很小,表明系统具有较好的控制性能,同时也验证了模型的正确性和控制方案的有效性。 [1] 王归新,康勇,陈坚.基于状态空间平均法的单相逆变器控制建模[J]. 电力电子技术,2004,38(5):9-12. [2] TULADHAR A, HUA J, UNGER T, et al.Control of parallel inverters in distributed AC power systems with consideration of line impedance effect[J]. IEEE Transactions on Industry Applications,2000,36(1):131-138. [3] GUERRERO J M, GARCIA D V L, MATAS J, et al.Output impedance design of parallel-connected UPS inverters with wireless load-sharing control[J]. IEEE Transactions on Industrial Electronics,2005,52(4):1126-1135. [4] GREGOIRE J M, LOBOVSKY M B, HEINZ M F, et al.Decentralized control for parallel operation of distributed generation inverters using resistive output impedance[J]. IEEE Transactions on Industrial Electronics, 2007, 54(2):994-1004. [5] PEI Y, JIANG G, YANG X, et al.Auto-master-slave control technique of parallel inverters in distributed AC power systems and UPS[C]//Power electronics specialists conference. Piscataway NJ: IEEE, 2004:2050-2053. [6] CHEN J F, CHU C L.Combination voltage-controlled and current-controlled PWM inverters for UPS parallel operation[J]. IEEE Transactions on Power Electronics,1995,10(5):547-558. [7] WU T F, CHEN Y K, HUANG Y H.3C strategy for inverters in parallel operation achieving an equal current distribution[J]. IEEE Transactions on Industrial Electronics,2000,47(2):273-281. [8] CHEN Y K, WU Y E, WU T F, et al.ACSS for paralleled multi-inverter systems with DSP-based robust controls[J]. IEEE Transactions on Aerospace and Electronic Systems,2003,39(3):1002-1015. [9] SUN X, LEE Y S, XU D H.Modeling, analysis, and implementation of parallel multi-inverter systems with instantaneous average-current-sharing scheme[J]. IEEE Transactions on Power Electronics,2003,18(3):844-856. [10]BEMPORAD A, MORARI M.Control of systems integrating logic, dynamics, and constraints[J]. Automatica,1999,35(3):407-427. [11]郑雪生,李春文,戎袁杰.DC/AC变换器的混杂系统建模及预测控制[J]. 电工技术学报,2009,24(7):87-92. [12]张聚,谢作樟,杨光利.DC/DC变换器混合逻辑动态建模与约束优化控制策略[J]. 电机与控制学报,2012,16(4):106-112. [13]马晓娟,吕智林,卢子广.独立运行的风/光/蓄微电网系统能量动态优化研究[J]. 广西大学学报(自然科学版),2013,39(2):431-438. [14]GEYER T, PAPAFOTIOU G, FRASCA R, et al. Constrained optimal control of the step-down DC-DC converter[J]. IEEE Transactions on Power Electronics,2008,23(5):2454-2464. (责任编辑 裴润梅) Modeling and optimal controlof parallel inverters of micro-grid based on MLD ZHOU Dong-lai, GONG Ren-xi, PENG Li-liang, LIU Chang (College of Electrical Engineering,Guangxi University,Nanning 530004,China) Aiming at the problems such as modeling precision and complexity of control scheme which lead non-satisfy control effect for the micro-grid inverter parallel system, a mixed logic dynamic(MLD)model based optimal control strategy is proposed for multi parallel operation of inverters supplying power in micro grid of distributed power. During the establishment of the MLD model, each PWM period is divided into several sub-periods, and the states of switches in each sub-period are judged by introduced auxiliary logic variables. Then the tool of HYSEDL is used to achieve the mixed logic dynamic (MLD) model. An appropriate predictive controller is designed according to natural constraints of the system and control objectives, and the control objectives of voltage tracking and current sharing are achieved by solving the corresponding mixed integer linear programming problem. Compared with the traditional modeling and control method, this method is characterized by high model precision of model, simple control scheme and better control result. The simulation results verify the validity of the model and the effectiveness of the proposed controller. micro-grid; parallel inverter; mixed logic dynamic; model predictive control 2016-04-15; 2016-05-06 国家自然科学基金资助项目(61561007) 龚仁喜(1962—),男,广西桂林人,广西大学教授,博士,博士生导师;E-mail:rxgong@gxu.edu.cn。 周东来,龚仁喜,彭立亮,等.基于MLD的微电网多逆变器并联组态的建模及优化控制[J].广西大学学报(自然科学版),2016,41(5):1485-1492. 10.13624/j.cnki.issn.1001-7445.2016.1485 TM615 A 1001-7445(2016)05-1485-082 基于MLD的模型优化控制
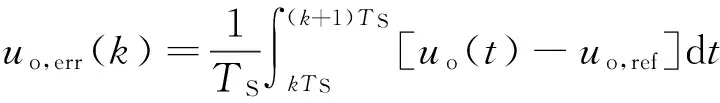
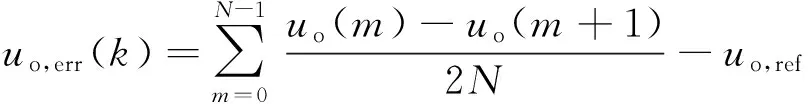


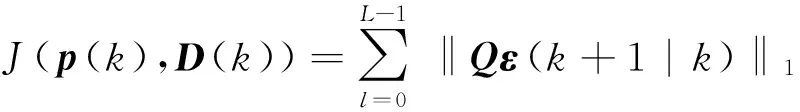

3 仿真验证
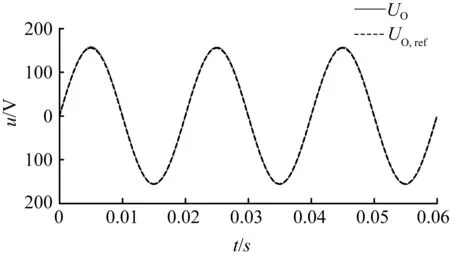

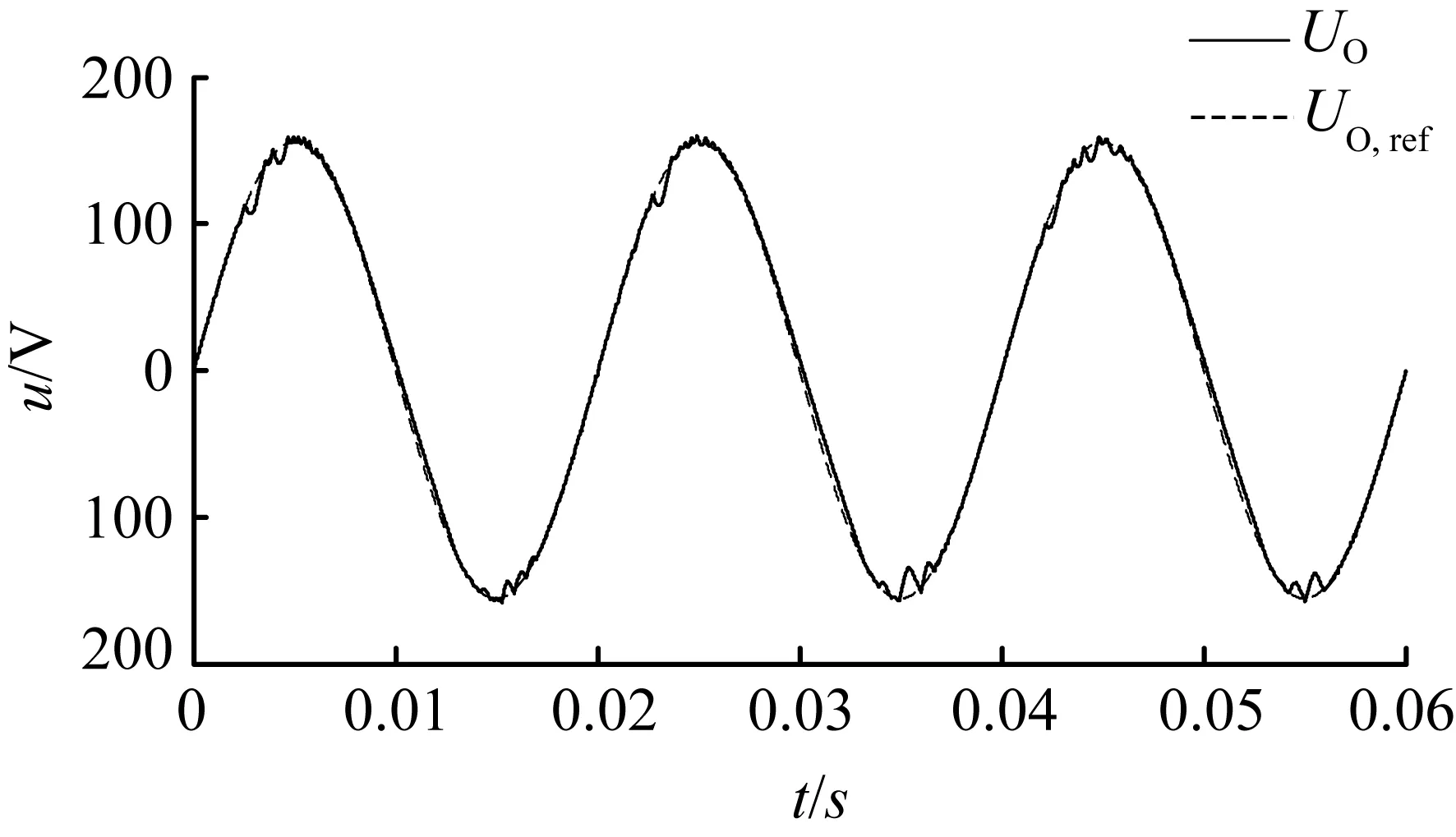


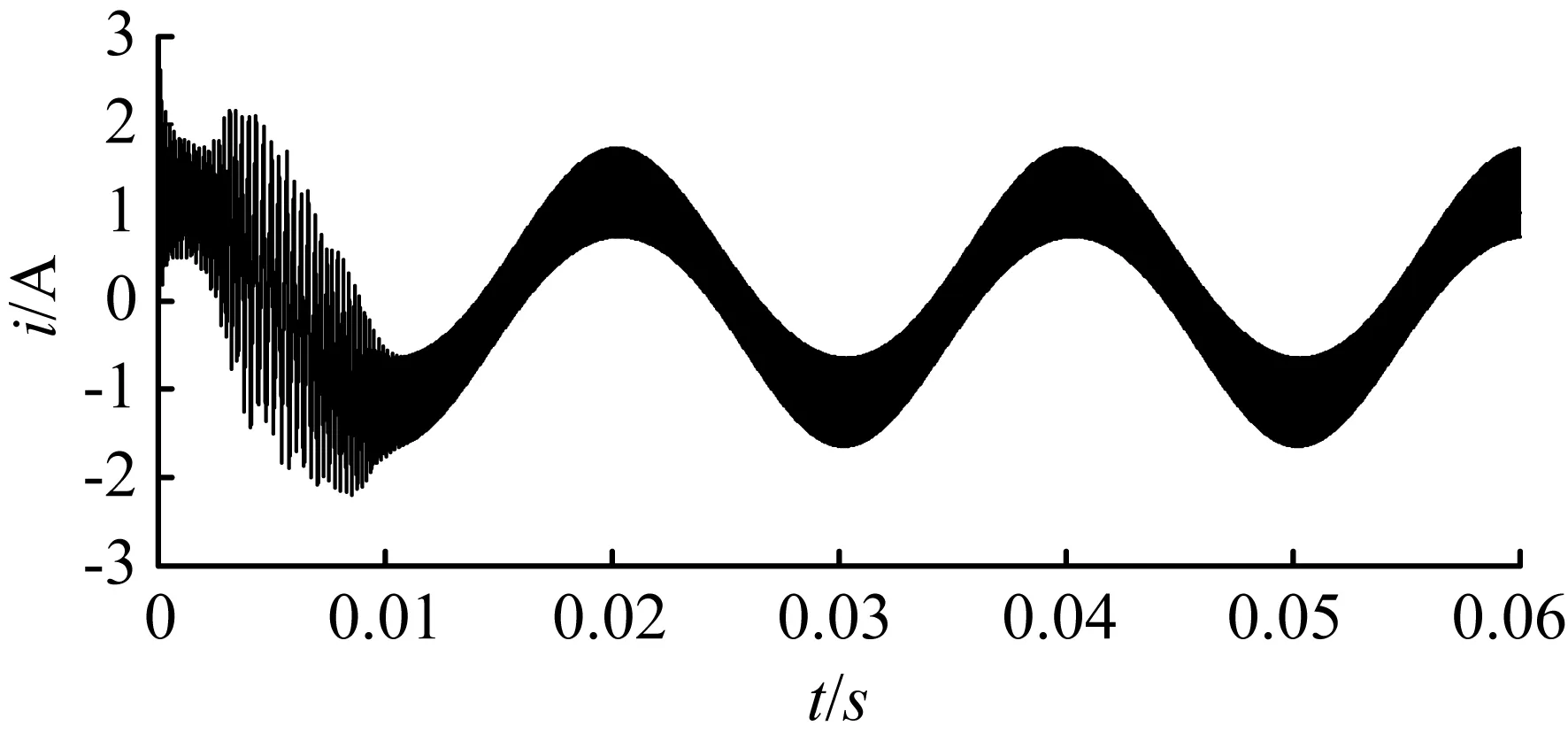
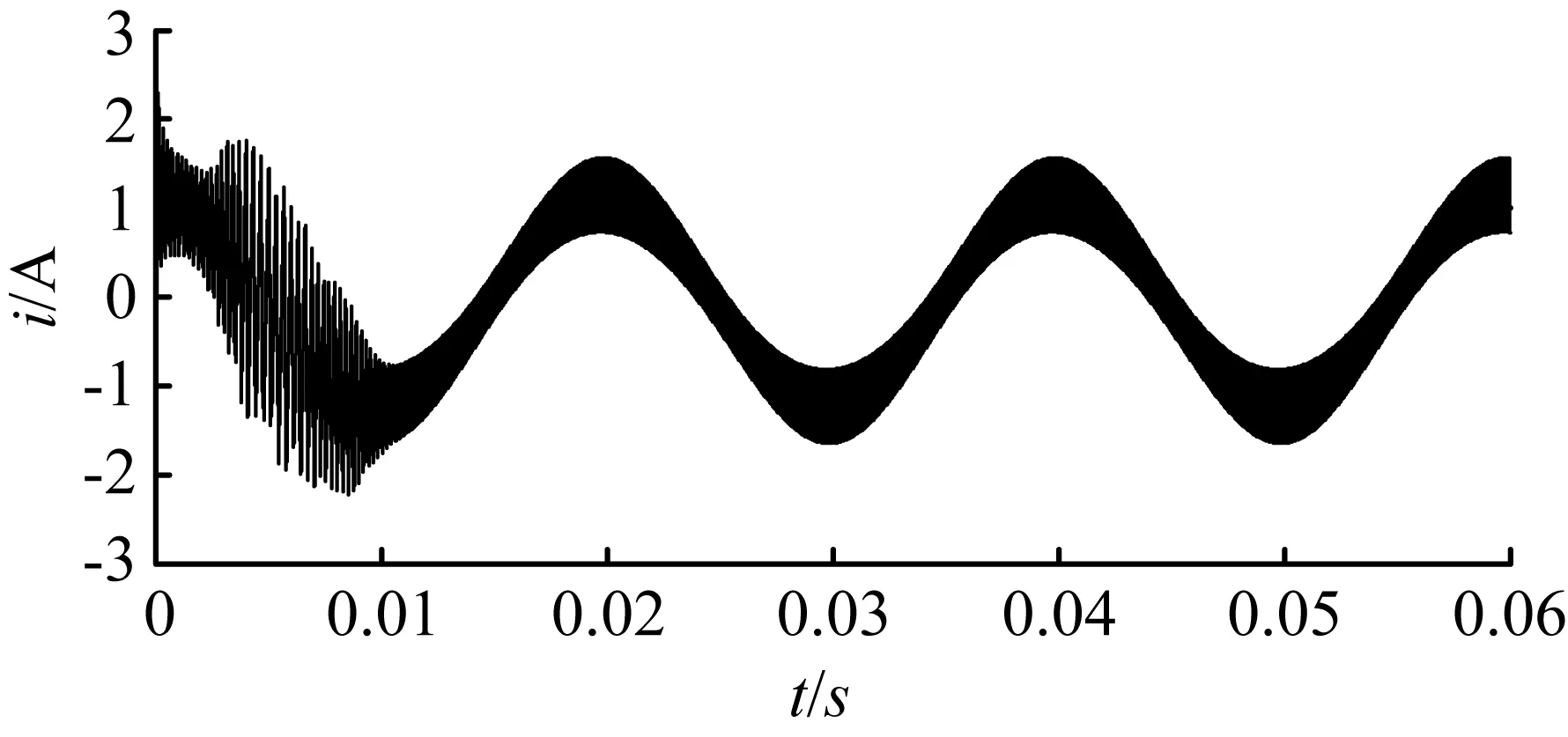
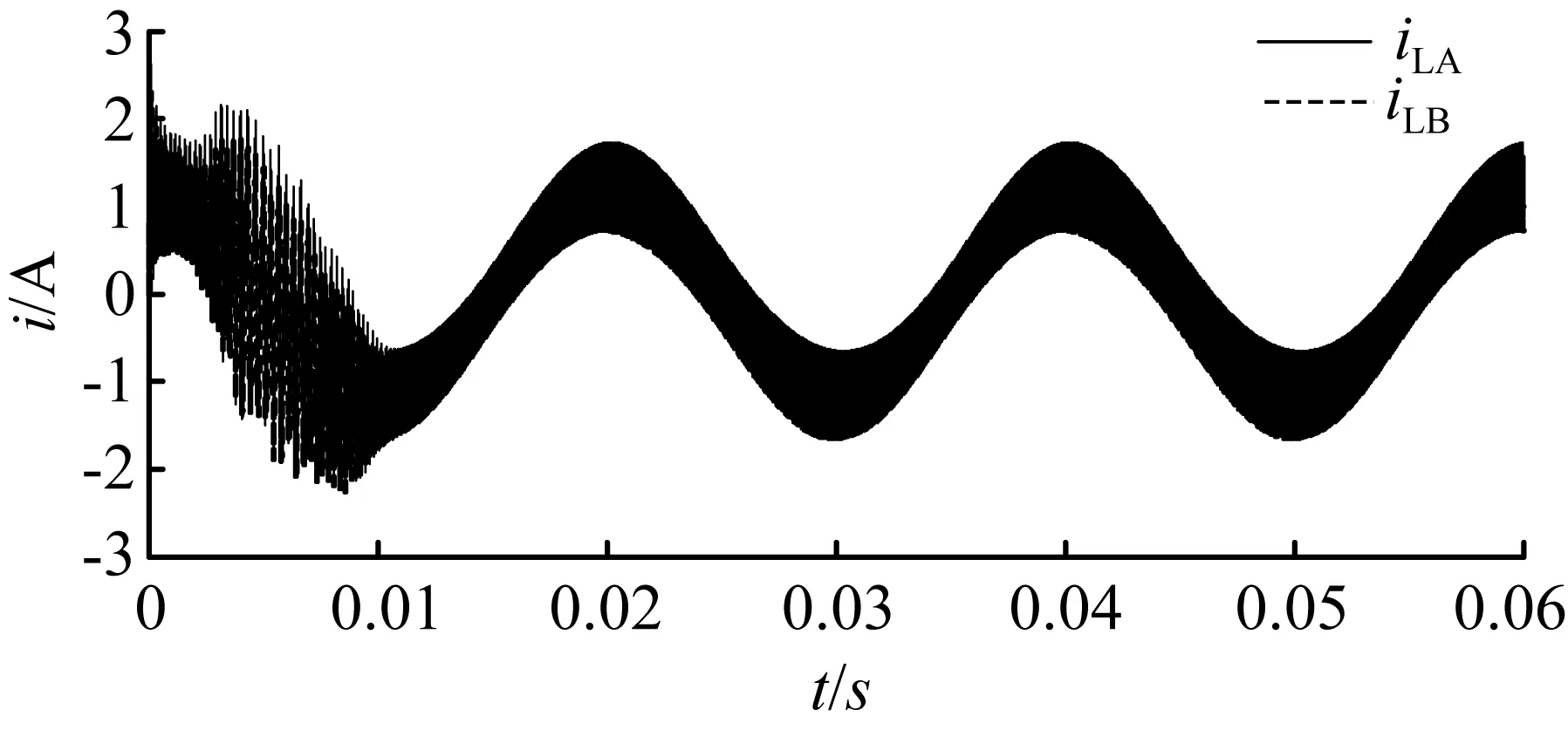

5 结 语

