“互联网+”背景下的废旧手机逆向物流网络设计

凌 旭，杨 斌，朱小林

(上海海事大学物流研究中心， 上海201306)



“互联网+”背景下的废旧手机逆向物流网络设计

凌 旭，杨 斌，朱小林

(上海海事大学物流研究中心， 上海201306)

在“互联网+”背景下，为促进互联网手机回收企业线下逆向物流网络优化布局，根据手机回收逆向物流网络结构及处理流程，建立了以互联网手机回收企业利润最大化和回收处理设施平均利用率最大化为目标的废旧手机逆向物流网络规划模型。考虑废旧手机档次和新旧程度等性质差异及政府补贴因素所带来的影响，结合案例并运用Lingo软件进行求解，得出了互联网手机回收企业回收中心和处理中心的优化选址方案。此时，互联网回收企业的总利润为1 841 824元，所选设施的平均利用率为95.67%。通过对回收量、回收价格及政府补贴3个因素的灵敏度分析，表明单个变量的变化对选址结果的影响较小，从而验证了模型和求解方法的有效性和可行性；但这3个因素对互联网回收企业利润的影响较大，为互联网手机回收企业策略选择提供参考。

互联网+；废旧手机；逆向物流；网络设计；政府补贴

0 引 言

随着科学技术的快速发展和市场竞争的日益激烈，人们对手机功能和外观的要求也在不断提高，这进一步加快了手机生产商技术革新的速度，同时手机更换周期也在不断缩短，尤其是智能手机的出现更是加速了手机更新换代的速度。据我国工业和信息化部统计，2014年我国共销售4.25亿部新手机，而新入网的手机用户仅为5698万，这就意味着存在大量的闲置废旧手机，这些手机大部分被闲置在家中，小部分被转手卖给小商贩，而通过正规渠道回收的手机比重更是少之又少。这些废旧手机的存在，一方面造成了巨大的资源浪费，同时对环境也是一种潜在的安全隐患。如何建立合理有效的逆向物流回收网络对废旧手机进行回收处理,已成为当前我国生态建设的重要课题之一。

当前国内外学者对电子废弃物回收逆向物流网络的研究已经取得了一定的成就。Jayaraman等[1]分析了美国电子产品再制造物流网络，对再制造网络中设施的数量、位置等进行了优化。Huseyin等[2]考虑了不同回收率下电子废弃物回收储存站点和回收设施的选址布局问题,提出了以总成本最小化为目标建立混合整数线性规划模型，并结合实例加以分析。Sibel等[3]研究了多阶段的电子废弃物逆向物流网络设计问题，以利润最大化为目标，考虑单阶段和多阶段情况下德国电子废弃物逆向物流网络模型，通过求解得出检测中心和再制造中心的选址。Berk等[4]考虑了逆向物流中电子废弃物回收量、分拣率和运输成本不确定的情况下，如何选择分拣中心和回收中心可以使第三方回收企业利润最大化。Li-Hsing[5]描述了台湾地区家用电器的管理现状和逆向供应链管理系统，提出一个混合整数规划模型(MIP)用于优化再生逆向物流系统的设施结果和物流分配。何波等[6]通过考虑产品回收逆向物流网络中的相关影响因素, 构建了非线性整数规划数学模型，并采用了嵌套模拟退火算法进行求解。高阳等[7]考虑了多周期多目标条件下第三方物流的产品回收网络模型，并采用目标规划法，分析了第三方物流供应商利益目标和原始设备制造商满意度目标两者之间的关系，研究了一方发生变化对另一方的影响。

在废旧手机回收方面，许志端等[8]以回收废旧手机产品为例，从第三方回收企业的角度考虑，研究了第三方回收企业运作的全过程，并构建了使第三方回收企业利润最大化的优化模型。邹筱[9]以废旧手机为例，建立了废旧手机回收的物流网络模型，并对广西地区的废旧手机回收问题进行了研究。戈姗姗[10]以手机生产企业逆向物流网络构建为研究主体，考虑单周期和多品牌因素，以最小化总成本为目标函数构建逆向物流网络模型，并采用遗传算法进行求解。孔荣娟[11]以陕西省废旧手机回收为例，探讨了不同回收率和拟建设施容量约束下的废旧手机逆向物流网络规划，提出了废旧手机回收率和逆向物流网络结构是影响废旧手机逆向物流网络规划的主要因素。

尽管手机也属于电器电子产品范畴，但目前国内外对废旧电器电子产品回收物流网络的研究主要集中在电视机、微型计算机、洗衣机、电冰箱、空气调节器(简称“四机一脑”)上，对废旧手机回收网络的研究相对较少，且研究主体多为手机制造企业或第三方物流回收企业，专门以新兴互联网回收处理企业为主体的文章相对较少。

随着国家发展和改革委员会等六部委于2015年2月9日公布的《废弃电器电子产品处理目录(2014年版)》的实施，将手机纳入到废旧电器电子产品中，这也就意味着手机回收也可享受和其他废旧电器电子产品回收一样的回收补贴。在利好政策的引导下，我国废旧手机回收市场迎来了一个崭新的春天，也给互联网手机回收带来了新的机遇。

本文以互联网手机回收处理企业为研究主体，互联网回收企业通过构建线上网络回收平台，并与线下回收网点相结合，整合线下线上两种资源对废旧手机进行回收再利用。为更好的促进回收企业选址优化，本文以互联网回收企业利润最大化和回收处理设施利用率最大化为目标建立多目标函数模型，并结合案例，通过运用Lingo11.0软件进行求解，以期为互联网回收企业的逆向物流网络设计提供参考。

1 问题描述

本文以互联网环境下的手机回收处理企业为主体，将互联网思维融入传统回收行业，通过构建网络回收平台建立线上手机报废网络，同时结合线下建立的回收点对消费者手中的废旧手机进行回收再利用。消费者可以通过微信、手机应用程序(APP)、网站等互联网回收渠道和方式进行快速投废，互联网回收企业迅速响应，并安排专业回收人员进行上门回收，然后对收集到的废旧手机进行检测分类，根据回收到的手机档次及新旧程度等情况，采用不同的处理方法进行资源化再利用。通过建立二手手机网络销售平台及零部件销售平台将可再利用的废旧手机销往二手市场、零部件回收企业及材料再生企业。具体回收网络结构如图1所示。

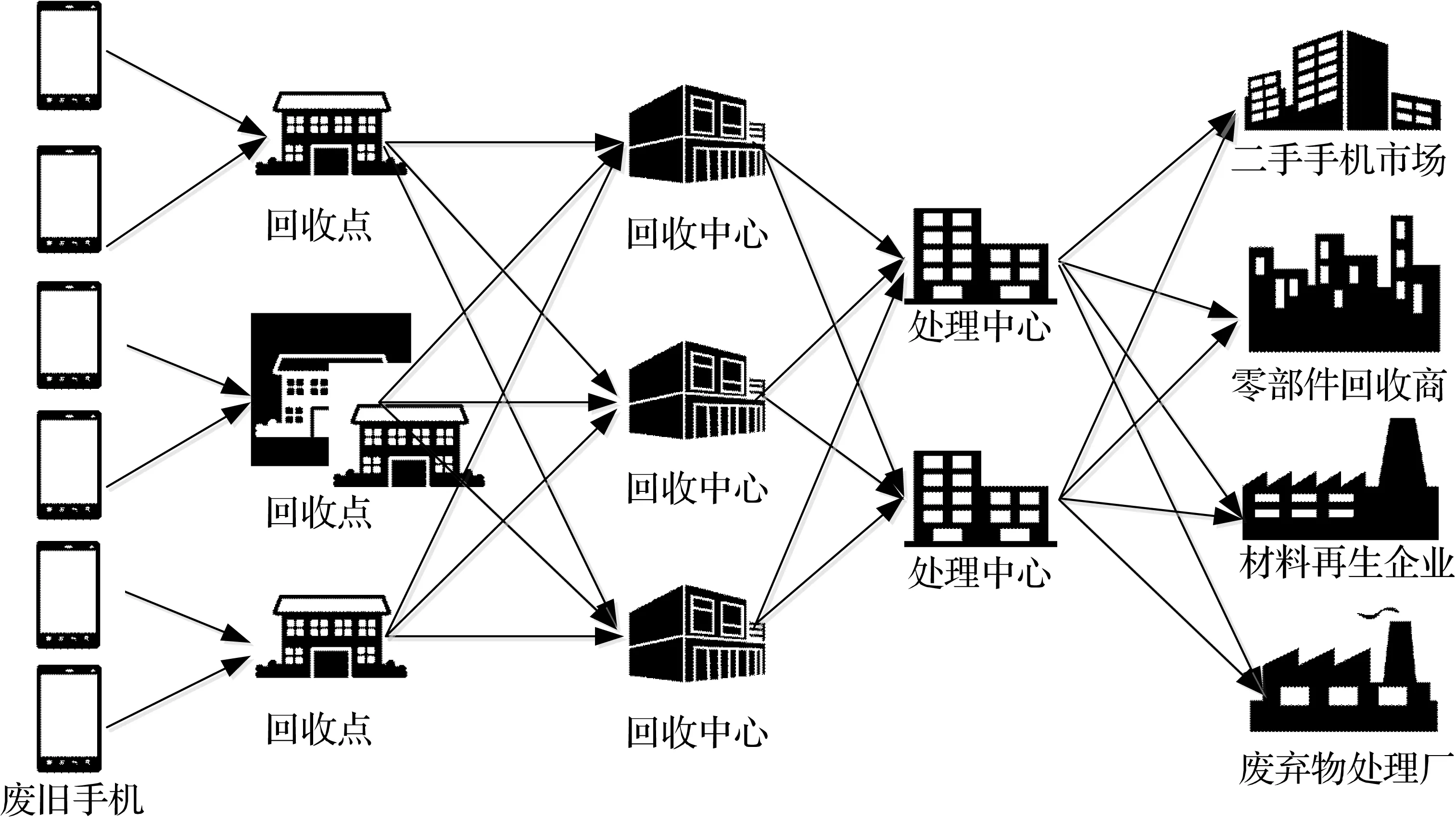
图1 废旧手机回收逆向物流网络结构图

本文所构建的网络是以互联网回收企业为主导的逆向物流网络：各消费区域内选定回收网点，负责此区域废旧手机的回收，消费者通过互联网回收平台进行网上报废，然后由回收点的工作人员进行上门回收并集中到回收点，再将回收的废旧手机运往相应的回收中心进行储存和检测分类，然后运往处理中心，在处理中心进行再处理，通过清洗、维修、翻新贴标和拆卸处理后，最终将处理产品运往相应的二手市场、零部件回收企业、材料再生企业和废弃物处理厂。具体回收处理流程如图2所示。

图2 废旧手机回收处理流程图

2 模型建立

本文在深入研究相关文献[12-15]的基础上,给出了废旧手机回收的逆向物流网络结构和处理流程,并在考虑不同档次、不同新旧程度废旧回收手机的基础上建立了逆向物流网络数学模型。此数学模型以逆向物流网络结构为基础,以单周期内逆向物流网络构建的利润最大化及设施利用率最大化为目标,考虑销售收入、收购成本、处理成本、运营成本、运输成本、固定成本及政府补贴等因素建立一个基于不同档次、不同新旧程度废旧手机回收逆向物流网络模型。模型优化的结果是要确定回收中心、处理中心的位置、数量以及彼此之间的网络流量分配。

2.1 模型假设

为了方便说明问题，现对废旧手机回收物流网络设计作如下假设：

假设1：所有回收处理活动都在已构建的规范化回收处理体系的范围内进行，且只考虑一个回收运营周期内的废旧手机回收情况；

假设2：考虑不同档次、不同新旧程度的废旧手机，根据品牌、功能、配置等方面差异将回收到的废旧手机分为高、中、低三种档次，根据废旧手机的外观、性能、新旧程度的差异，将收到的废旧手机分为四类，即完全不能使用、三成新、六成新和九成新；

假设3：考虑运输成本、设施固定成本、单位运营成本等经济成本，回收点的单位运营成本包括回收点工作人员上门回收的人工成本，且该平均成本已知，设施间的运输成本与设施间的距离及运输量呈一定的比例关系，不考虑时间成本；

假设4：回收点、二手手机市场、零部件回收企业、材料再生企业及废弃物处理厂的地理位置及数量已知，仅在备选地址中考虑回收中心和处理中心的选址，且各备选回收中心、处理中心的存储能力和处理能力是有限的；

假设5：不考虑二手手机市场、零部件回收商及材料再生企业对废旧手机、零部件、材料的需求限制，由于整个回收网络中废弃物产生的量较少，废弃物处理厂的处理能力足以满足要求，故对废弃物处理厂的处理能力不作要求，即其处理能力是无限的；

假设6：政府给予互联网手机回收企业一定的政策扶持和回收补贴，且回收补贴金额与处理中心拆解的废旧手机数量有关。

2.2 符号说明

2.2.1 集合变量

I为互联网回收企业在消费区域设立的回收点集合，i∈I；R为可能设立的回收中心集合，r∈R；P为可能设立的处理中心集合，p∈P；L为回收到的废旧手机档次集合，l∈L={1,2,3}；Q为回收到的废旧手机新旧程度集合，q∈Q={1,2,3,4}；S为二手手机市场集合,s∈S；C为可供选择的零部件回收商集合,c∈C；M为资源再生企业集合，m∈M；D为废弃物处理厂集合,d∈D。

2.2.2 模型参数

Pql为新旧程度为q档次为l的废旧手机的单位收购价格(元/台)；Sql为新旧程度为q档次为l的废旧手机经过处理中心专业处理后销往二手手机市场的单位销售价格(元/台)；S1为处理中心经过拆解后的零部件的单位平均销售价格(元/kg)；S2为处理中心经过拆解后产生的材料的单位平均销售价格(元/kg)；Dir为从回收点i到回收中心r的距离；Drp为从回收中心r到处理中心p的距离；Dps为从处理中心p到二手手机市场s的距离；Dpc为从处理中心p到零部件市场c的距离；Dpm为从处理中心p到材料市场m的距离；Dpd为从处理中心p到废弃物处理厂d的距离；MC1l为回收到的l档次的废旧手机在回收点处的平均运营成本(元/部)；MC2l为回收到的l档次的废旧手机在回收中心处的平均运营成本(元/部)；MC3l为回收到的l档次的废旧手机在处理中心处的平均运营成本(元/部)；C1为废旧手机维修翻新的单位处理成本(元/部)；C2为废旧手机中零部件拆解翻新的单位处理成本(元/部)；C3为废旧手机维修拆解过程中产生的废弃物的委托处理成本(元/kg)；FCi为建立回收点i的固定成本(元)；FCr为建立回收中心r的固定成本(元)；FCp为表示建立处理中心p的固定成本(元)；GS为表示政府对互联网回收企业的单位回收补贴(元/部)。

2.2.3 决策变量和约束条件

Ri为0-1变量，表示是否选择在i地设立回收点，选中取1，否则取0；Rr为0-1变量，表示是否选择在r地设立回收中心，选中取1，否则取0；Rp为0-1变量，表示是否选择在p地设立处理中心，选中取1，否则取0；Xirl为回收点i运往回收中心r的l档次的废旧手机的数量(部)；Yrpl为回收中心r运到处理中心p的l档次的废旧手机的数量(部)；Zpsl为经过处理中心p专业处理后销往二手手机市场的l档次的手机的数量(部)；Ipc为处理中心p销售给零部件回收商c的零部件重量(kg)；Jpm为处理中心p出售给资源再生企业m的材料重量(kg)；Kpd为从处理中心p运往零部件回收商废弃物处理厂d的废弃物重量(kg)。

2.2.4 其他参数设置

Ail为消费区域回收点i回收到的档次为l的废旧手机的数量(部)；θql为回收中心回收到的新旧程度为q档次为l的废旧手机的概率(%)；TC为单位重量、单位距离的运输成本[元/(kg·km)]；G为废旧手机的单位平均重量(kg)；γ1p为经过处理中心p维修翻新后再销售的整机重量比例(%)；γ2p为经过处理中心p拆解的零部件再销售的重量比例(%)；γ3p为经过处理中心p拆解的材料再循环的重量比例(%)；γ4p为处理中心p产生的废弃物重量比例(%)；α为回收中心的平均利用率系数；β为处理中心的平均利用率系数；Ur为单周期内回收中心的最大回收能力(部)；Up为单周期内处理中心的最大处理能力(部)。

2.3 目标函数和约束条件

(1)

(2)

s.t.

(3)

(4)

(5)

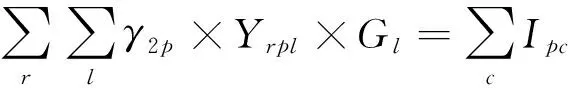
(6)

(7)

(8)

γ1p+γ2p+γ3p+γ4p=1 γ1p,γ2p,γ3p,γ4p≥0

(9)

(10)

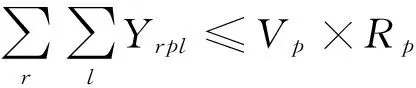
(11)

Xirl,Yrpl,Zpsl,Ail,Ipc,Jpm,Kpd,Gl≥0 ∀i,r,p,s,c,m,d,l

(12)

Ri,Rr,Rp∈{0,1} ∀i,r,p

(13)

其中：式(1)表示整个回收网络中互联网手机回收企业的利润最大化，等式右边自上而下依次是整机、零部件的销售收入、废旧手机的收集成本、整机翻新和零部件拆解的处理成本、废弃物委托处理成本、各物流节点的运营成本、各节点之间的运输成本、各回收处理节点的固定成本及政府补贴；式(2)表示回收中心和处理中心的设施平均利用率最大，主要包括回收过程中各回收中心的检测设备利用率与处理中心的拆解设备利用率；式(3)～(9)表示各物流节点的物质量守恒，即各回收点、回收中心、处理中心的废旧手机输入量等于输出量；式(10)和(11)规定了回收中心和处理中心的最大处理能力限制；式(12)～(13)规定了各变量的取值范围。

2.4 模型求解

上述模型属于多目标混合整数规划模型，多目标规划问题一般很难找到一个最优解，只能在协调各个目标函数的基础上尽可能的接近理想解，即得到一个pareto最优解。本文根据文献[14],运用模糊理论中的模糊隶属度函数对目标函数进行模糊化处理，将多目标问题转化为单目标问题进行求解。具体步骤如下：

步骤1：当仅考虑单个目标时，利用Lingo软件分别求得各目标函数的取值区间。首先当仅考虑目标一时，通过编程计算得到第1个目标函数的取值范围为[F1min,F1max]；同理，当仅考虑目标二时，通过编程计算得到第二个目标函数的取值范围为[F2min,F2max]。

步骤2：采用隶属度模糊化函数方法，对每个目标函数分配一个模糊愿望值，用模糊愿望的隶属度来表示决策者对相应目标水平的满意程度。本模型属于求最大值优化问题，其模糊愿望的隶属度函数为：

(14)

(15)

步骤3：赋予目标满意度不同的权重系数，将各目标的满意度统一到一起组成整体满意度，以实现多目标转化为单目标。即：maxF=ω1μ1+ω2μ2,其中ω1、ω2分别为两个隶属度模糊化函数的权重系数，表示目标函数的相对重要程度，由互联网回收企业根据回收情况及消费者回收响应度综合分析给出。

步骤4：利用Lingo11.0求解新的目标函数。

3 算例分析

3.1 算例描述

已知某互联网手机回收企业拟在S城市布局手机回收处理网络，该城市可分为10个消费区域，该企业已在每个消费区域的中心设立了一个回收点，且每个回收点能覆盖大部分消费区域。该回收企业现有5个回收中心备选地址，3个拟建的备选处理中心地址，为降低成本，提高回收效率，该企业打算从这5个备选回收中心中选择3个作为回收中心，从3个拟建处理中心中选择2个作为处理中心。根据各回收点的互联网平台回收数据分析与预测，给出各回收点高、中、低档废旧手机的回收数量、不同新旧程度废旧手机的回收比例及回收价格，整机翻新成本为10元/部，零部件拆解及翻新的处理成本为5元/部，废弃物委托处理成本为20元/kg，拆解后销售给零部件回收商的零部件单位价格为50元/kg，出售给材料再生企业的拆解材料价格为30元/kg，回收点、回收中心、处理中心的平均运营成本分别为15元/部、3元/部、5元/部，各设施之间的单位运输费率为1元/(kg·km)，政府为鼓励互联网回收企业给予其处理中心拆解的废旧手机补贴为5元/部，高、中、低三档手机的平均重量分别为125 g、150 g和180 g，各处理中心运往废旧手机二手市场、零部件市场、材料再生企业及废弃物处理厂的废旧手机重量比例分别为40%、30%、20%、10%，设定回收中心的平均利用率系数α=0.6，处理中心的平均利用率系数β=0.4。其他相关数据如表1～表8所示。

表1 各回收点收集到的不同档次废旧手机数量Ail

表2 回收中心不同档次不同新旧程度废旧手机的回收比例θql

表3 不同档次不同新旧程度废旧手机的回收价格及翻新后的再销售价格 (Pql,Sql)/(元·部-1)

注：完全不能使用的手机无翻新价值，故翻新再销售价格为0，但可以经过拆解后对可利用的零部件及材料进行再销售。

表4 回收点到备选回收中心之间的距离

表5 备选回收中心到处理中心之间的距离

表6 备选处理中心到各相关物流设施节点之间的距离

表7 各物流设施的固定成本

表8 备选回收中心或处理中心最大处理能力

3.2 算例求解

3.2.1 算例结果

通过运用Lingo软件进行编程求解可得，当两个目标函数的权重为(1,1)时，选择备选回收中心1、3、5和处理中心1、3作为整个回收网络的回收中心和处理中心，此时互联网回收企业的总利润最大为1 841 824元，所选回收中心和处理中心的设施平均利用率为95.67%。具体回收处理设施选址及流量分配如图3所示。

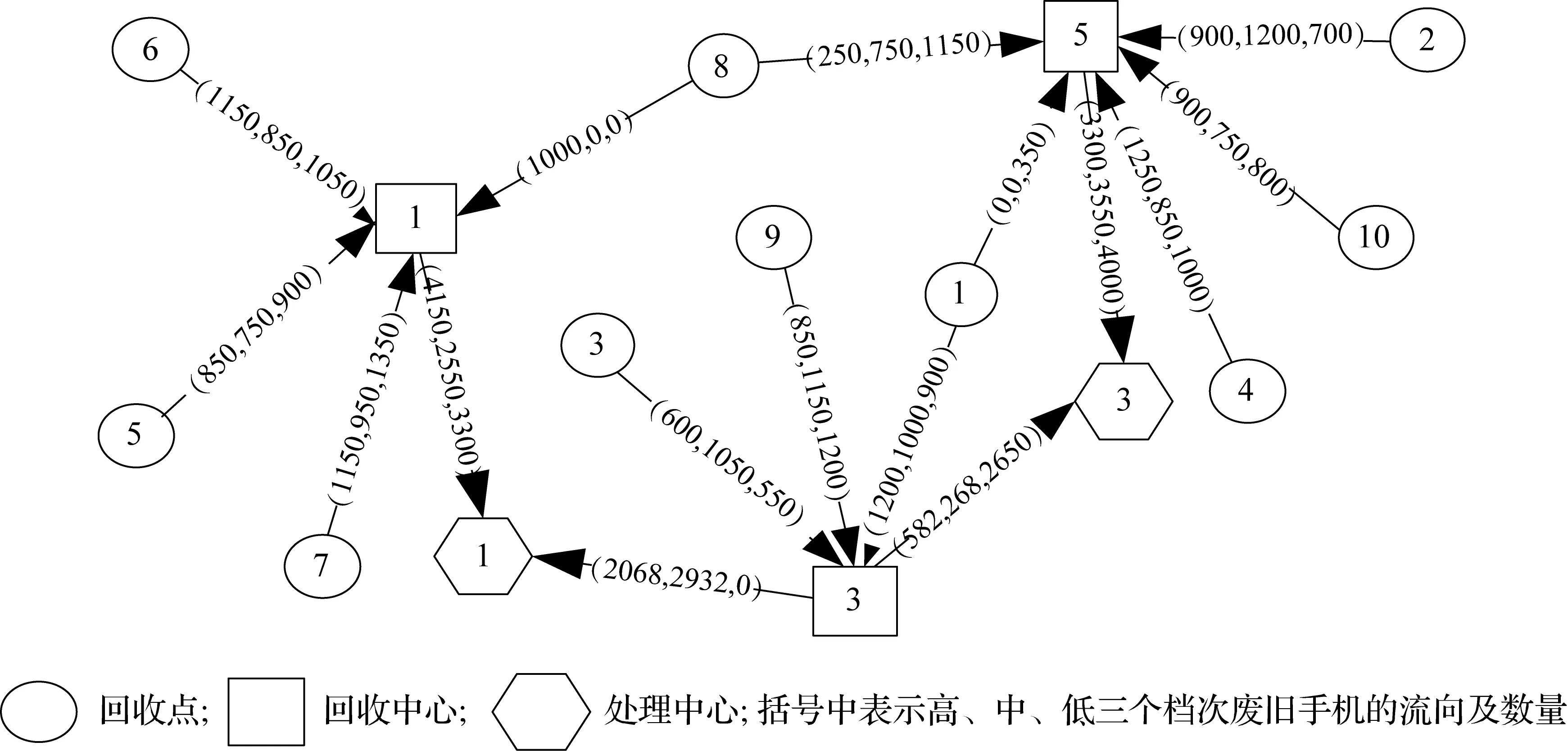
图3 最优物流网络选址及流量分配图

3.2.2 权重变化对设施选址的影响

通过运用Lingo软件，对不同权重下的目标函数进行求解，得出三种权重下的物流网络设施选址方案及对应的互联网回收企业利润和回收处理设施利用率的目标函数值。如表9所示。

由算例可知回收处理设施的平均利用率与回收到的废旧手机数量相关，回收的废旧手机数量越多，设施的平均利用率就越高，而整个回收网络的总利润也与回收数量息息相关，且关系度大于回收处理设施利用率。因此，作为新兴的互联网回收企业，应该充分利用互联网回收平台优势，采取高效、便捷、安全的回收方式和宣传策略，促进消费者积极投废，增加整个回收网络的回收量，尽可能的满足回收处理设施的利用率，降低检测和拆解设备闲置率，才能最大程度的提高整个回收网络的总利润和回收运作效率。

表9 物流网络设施选址方案

注：√表示选中该物流设施。

3.2.3 灵敏度分析

为了分析回收量、回收价格及政府补贴变化对整个回收网络选址及总利润的影响，本文对三者分别进行了灵敏度分析。首先对回收量减少15%、减少10%、减少5%、不变、增加5%、增加10%等6种情况进行了对比分析，如图4所示，在其他条件不变的情况下，随着废旧手机回收数量的增加，销售收入、收购成本及总利润都在增加。通过运用Lingo程序进行编程计算得知，当回收量减少时回收处理中心选址均保持不变；而当各回收点的回收量增加5%和10%时，回收中心选址分别为备选回收中心3、4、5和备选回收中心1、4、5，处理中心选择均为备选处理中心1和3。因此，在本案例中回收量的变化对回收中心的选址影响较大，而对处理中心选址的影响较小。其次，通过对平均回收价格±20%、±10%及不变5种情形下总回收成本及总利润的变化情况进行分析，表明随着回收价格的增加，回收成本也会相应增加，回收总利润也会降低，如图5所示。通过运用Lingo程序进行编程计算得知，回收价格变化对回收中心和处理中心选址影响较小，在以上5种情况下，回收中心和处理中心选址均保持不变。最后分析了政府补贴金额为0、2、5、10、15、20元时的总利润变化情况，如图6所示，随着政府补贴额度的增加，互联网回收企业的总利润也会相应提高，其回收积极性也会相应提高。由Lingo编程计算得知，政府补贴金额对回收处理中心选址影响较小，在以上6种情况下，回收中心和处理中心选址均保持不变。通过上述灵敏度分析及程序实现结果分析可知，单个变量的变化对选址结果的影响较小，但对互联网回收企业利润的影响较大，因此该模型具有较高的稳定性。

图4 回收量变化的灵敏度分析

图5 回收定价变化的灵敏度分析

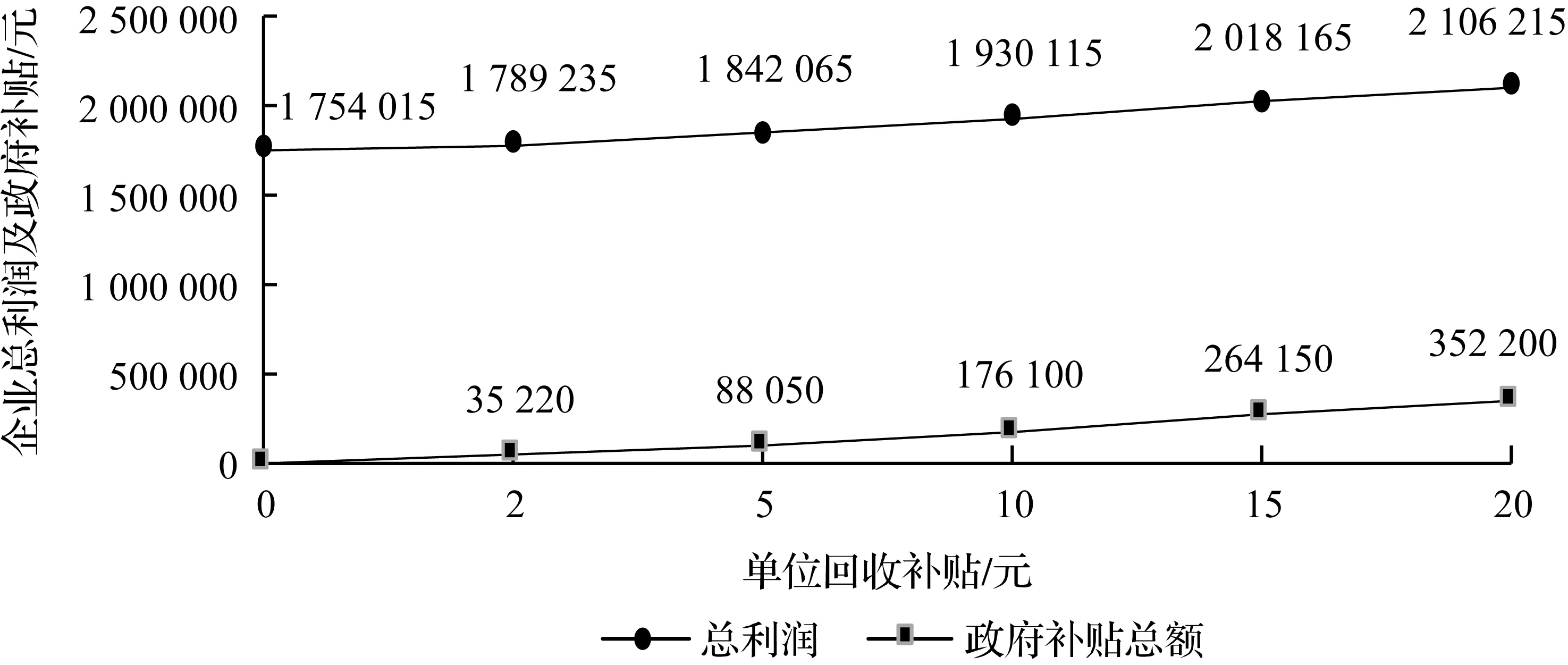
图6 政府补贴金额变化的灵敏度分析

4 结 论

随着“互联网+手机回收”的不断发展，互联网手机回收行业正面临新一轮的整合与挑战。如何在激烈的互联网手机回收市场上获得竞争优势，最主要的是要解决其网络设计问题。本文着重考虑了废旧手机档次和新旧程度的差异对回收价格和再销售价格的影响，同时考虑了政府补贴因素对互联网回收的影响，与其他相关研究相比更具有现实意义。在本文中，首先分析了手机回收网络结构和流程，然后在考虑不同回收档次、不同新旧程度废旧手机和政府补贴的基础上，以互联网手机回收企业利润最大化及回收处理设施平均利用率最大化为目标，建立了废旧手机逆向物流网络多目标数学模型，并结合案例运用Lingo软件进行求解，得出了不同权重系数影响下的互联网手机回收企业线下的逆向物流回收网络的回收中心和处理中心选址优化方案。并通过Lingo软件计算得出了同时考虑互联网手机回收企业利润最大化和回收处理设施平均利用率最大化时，互联网回收企业的总利润为1 841 824元，所选设施的平均利用率为95.67%。

通过对回收量、回收价格及政府补贴的灵敏度分析，表明在其他条件不变的情况下，回收量减少15%、减少10%、减少5%、不变、增加5%、增加10%时处理中心选址均为1和3，回收中心选址也基本保持不变；通过对平均回收价格±20%、±10%及不变五种情形及政府补贴金额差异时选址结果的分析，得出在上述情况下，回收中心和处理中心选址均保持不变。因此，单个变量的变化对选址结果的影响较小，从而验证了网络设计的有效性，促进了回收网络的优化布局。但回收量、回收价格和政府补贴的变化对互联网手机回收企业的利润影响较大，单个变量变化都会影响互联网手机回收企业的总利润。因此，作为互联网手机回收企业，应在充分考虑政府补贴影响的基础上，采取积极的营销和宣传策略，制定合理的回收定价规则，优化服务质量，提高服务水平，从而增加废旧手机的回收量，提高企业的总利润和市场竞争力，促进企业高效快速发展。

[1] JAYARAMAN V，GUIDE Jr V D R，SRIVASTAVA R.A closed-loop logistics model for remanufacturing[J]. Journal of the Operational Research Society，1999，50(1)：497-508.

[2] HUSEYIN S K，UFUK C，MUSTAFA B A.Reverse logistics system design for the waste of electrical and electronic equipment (WEEE) in Turkey[J]. Resources，Conservation and Recycling，,2015，95(1)：120-132.

[3] SIBEL A，STEFAN N，FRANCISCO S G, et al.Multi-period reverse logistics network design[J]. European Journal of Operational Research，2012，220(1)：67-78.

[4] BERK A，BERSAM B，NEZIR A.Stochastic reverse logistics network design for waste of electrical and electronic equipment[J]. Resources，Conservation and Recycling，2015,104(Part B)：391-404.

[5] LI-HSING S.Reverse logistics system planning for recycling electrical appliances and computers in Taiwan[J]. Resources，Conservation and Recycling，2001，32(1)：55-72.

[6] 何波，杨超，任鸣鸣.基于第三方物流的产品回收物流网络优化模型及算法[J]. 计算机集成制造系统，2008，14(1)：39-44.

[7] 高阳，詹沙磊.基于第三方物流的多周期多目标产品回收网络设计[J]. 控制与决策，2010，25(8)：1164-1168.

[8] 许志端，郑腾.电子废旧品第三方回收企业的盈利模型[J]. 管理现代化，2008(2):12-14.

[9] 邹筱.小件电子产品回收物流网络模型与实证研究[J]. 工业经济研究，2012，25(2)：136-141.

[10]戈姗姗.废旧手机逆向物流网络构建研究[D]. 北京：北京交通大学,2011.

[11]孔荣娟.以废旧手机为例的电子废弃物逆向物流网络规划[D]. 西安：西安电子科技大学，2014.

[12]代颖，马祖军.废旧家电回收处理体系及管理机制[M]. 北京：科学出版社，2010.

[13]高阳，周向红，李辉.基于动态定价的再制造商主导的多周期多目标产品回收网络设计[J]. 运筹与管理，2014，3(6)：64-70.

[14]徐玖平，李军.多目标决策的理论与方法[M]. 北京：清华大学出版社，2005.

[15]潘静静，胡志华.集材区选址与能力配置的集成优化问题[J]. 广西大学学报(自然科学版)，2015,40(6)：1533-1539.

[16]周静娴，肖玲，胡志华.基于双层随机规划的多时段募集点选址问题[J]. 广西大学学报(自然科学版)，2014, 39(2):365-371.

(责任编辑 梁 健)

The design of reverse logistics network of used mobile phone in the background of Internet plus

LING Xu， YANG Bin，ZHU Xiao-lin

(Logistics Research Center, Shanghai Maritime University, Shanghai 201306, China)

In order to improve the optimal allocation of the offline reverse logistic network of Internet mobile phone recycling enterprise under the background of “Internet+”, according to the structure and processing procedure of mobile phone recycling reverse logistic network, the used mobile phone reverse logistics network programming model, which regards the profit maximization of Internet mobile phone recycling enterprise and utilization maximization of recycling processing facilities as targets, is designed. Considering the property difference such as the class and condition of used mobile phones as well as the government subsidies, based on some cases, it applies Lingo software to find out the optimal address selection planning for the recycling center and processing center of Internet mobile phone recycling enterprise. In this case, the total profit of the Internet mobile phone recycling enterprises is RMB 1 841 824, the average utilization rate of the selected facilities is 95.67%. Besides, through the Sensitivity Analysis on recycling quantity, price and sensitivity of government subsidies during the phone recycling process, it showed that the change in a single variable has little effect on the location results, thus this verify the validity and feasibility of the model and solution methods. However, it has a greater impact on the Internet mobile phone recycling enterprises profits recovered the Internet, so as to provide reference for the Internet mobile phone recycling business strategy selection.

Internet plus; mobile phone recycling; reverse logistics; network design; government subsidies

2016-04-09；

2016-05-19

国家自然科学基金资助项目(71171129)；交通运输部科技项目(2015328810160)；上海市科委科研计划项目(14DZ2280200, 14511107402)；上海市自然科学基金资助项目(15ZR1420200)

杨 斌(1975—),男，山东招远人，上海海事大学教授，博士生导师；E-mail：binyang@shmtu.edu.cn。

凌旭，杨斌，朱小林.“互联网+”背景下的废旧手机逆向物流网络设计[J].广西大学学报(自然科学版)，2016，41(5)：1465-1476.

10.13624/j.cnki.issn.1001-7445.2016.1465

F252

A

1001-7445(2016)05-1465-12