层次分析法在购房决策中的应用

李天赐

安徽理工大学经管学院，安徽淮南，232001



层次分析法在购房决策中的应用

李天赐

安徽理工大学经管学院，安徽淮南，232001

为指导消费者购房,在调查济南市市民购房需求的基础上，确定房价、户型等9种购房指标，基于层次分析法，构建济南市五大市区购房选择的递阶层次模型。利用问卷调查和专家经验评测法量化购房因素，构造两两比较的判断矩阵。利用和方法计算购房因素的权重及其一致性。然后计算购房指标及其各个市区指标对购房目标的排序权重，依照权重大小进行购房总层次排序及其一致性检验。结果表明，济南购房权重顺序为：历下区>历城区>长清区>市中区>槐荫区，即历下区住房性价比最高，其次是历城区、长清区和市中区，槐荫区住房最差，消费者在购房决策时可以优先选择历下区。

购房决策；层次分析法；问卷调查法；专家评测

古往今来，衣食住行始终是人们关注的焦点，人们对于住房更是情有独钟。如今房地产市场的发展更是如火如荼，房价居高不下，从侧面衬托了人们对住房的需求。婚嫁以及高品质生活的需要，众多的人在城市购房，再加上我国人口基数大，导致购房需求巨大。然而购房资金巨大，人们的资金普遍不充裕，需要考虑的问题众多，如房价、户型、升值空间、子女教育、医疗、超市配置、交通情况、居住环境、地理位置等因素，这些因素导致人们一时无法快速准确地作出购房决策。最重要的是这些购房因素除房价之外，其他的既无量化数据，又无有价值的理论参考，购房者只能凭借个人经验或者自我主观感受粗略地作出决策，很大程度上无法选择最佳的房源，甚至造成重大损失，因此急需科学的理论方法用于购房决策分析。

1　相关理论与研究

1.1层次分析法

20世纪70年代，T.L.Saaty提出一种系统化、层次化、定量和定性相结合的分析方法——层次分析法，简称为AHP[1]。在人们的思维过程和主观判断中，AHP可以实现规范化和数量化来确定权重,并结合专家客观判断，针对性地分析系统因素，计算具有相互联系的各种因素的有序层次和相对权重，最终建立有效的数学模型。然后准确计算每层因素的相对重要性的权重，并根据各因素的权重进行排序，最后分析排序结果。由此选择相对较好的方案进行决策，以期解决所要研究的相关问题。简而言之，运用AHP可以快速准确地处理复杂的决策问题。

1.2购房决策的相关研究

我国学者对购房决策的研究已取得了显著成果。陈江涛讨论了影响消费者购房的决策因素，并提出了一些房地产营销的重要建议[2]。李宏勋将博弈论应用于购房决策中，分析消费者和地产商需要考虑的主要购房指标，进而提出各自的策略[3]。丁香乾等在项目风险管理中应用层次分析法解决项目风险问题，规范项目风险指标，减少不必要的资金损失[4]。为了丰富购房决策理论研究，本文采用多层次分析法分析济南市的购房决策，运用问卷调查收集相关数据，并结合专家评价打分，计算权重，量化济南五大市区的购房指标，给现在或者将来在济南购房的人们提供参考建议。

2　建立购房选择模型

2.1购房建模步骤

首先建立购房递阶层次的结构模型，其次以购房因素数据化构造购房判断矩阵，然后依次进行购房因素层次单排序和一致性检验，最后进行购房层次总排序和一致性检验。

2.2递阶层次购房结构模型的建立

把购房因素层次化，构建一个有层次结构的购房模型，将其中的购房因素分成按照一定属性及相关关系组成的若干层次。

(1)最高层：目标指数是购房，购房是分析问题的预定目标。

(2)准则层：房价、户型、升值、子女教育、医疗、超市配置、交通情况、居住环境、地理位置。

(3)方案层：含市中区、历下区、历城区、槐荫区、长清区。

2.3构造购房判断矩阵

依据以上建立的递阶层次购房结构模型，依次两两比较结构模型的购房因素建立成对比较矩阵，利用数值1～9及它的倒数来量化两两比较矩阵中的购房因素的相对关系。赋值标准如表1所示。

表1　购房判断矩阵中因素的赋值标准

2.4购房的层次单排序及其判断矩阵一致性检验

层次单排序的目的是用来计算判断矩阵因子相对应的最大特征值所对应的特征向量W，然后把购房模型中同层次的因素对上一层次指标相对重要性归一化为排序权值[5]。

从理论上说，计算排序权向量的依据就是判断矩阵，而判断矩阵的数据难免出现误差和数据的不一致性。为确定判断矩阵是否正确、数据是否合理，必须进行一致性检验。

(1)判断矩阵一致性指标：

CI=(λmax-n)/(n-1)

其中CI的数值愈小，说明判断矩阵的一致性越大，数据越合理。

(2)查询不同矩阵的阶数n相应的平均随机一致性指标RI数值，具体相对应的RI值如表2所示。

表2　不同矩阵的阶数n相对应的RI值

(3)计算一致性比值：

CR=CI/RI

当CR数值<0.10时，判断矩阵的一致性是合理的，可以进行下一步计算，否则，必须重新合理地修正判断矩阵，直到一致性比值CR<0.10。

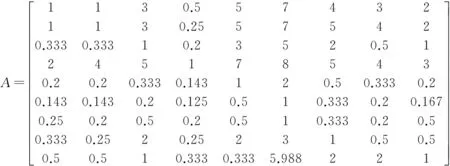
(4)采用和方法(每一列归一化后近似权重)计算各指标权重。

第一步：按照矩阵的列对A矩阵的数据进行归一化。

第二步：将归一化后的矩阵的各行相加。

第三步：将相加后的矩阵结果除以矩阵维数n，可以得到矩阵最终权重向量。

2.5购房模型总排序及其数据的一致性检验

依据以上和方法计算得出的各指标的权重向量，自上而下将各个准则层的权重进行合成，得到各指标尤其是最底层市区指标对购房目标的排序权重，参考排序权重进行购房方案最佳选择。

(1)各元素总权重的计算，假设购房模型各权重向量为：

准则层∂j=(∂1，∂2，∂3，∂4，∂5，∂6，∂7，∂8，∂9)

方案层bij=(b1j，∂2j，∂3j，∂4j，∂5j，∂6j，∂7j，∂8j，∂9j)

式中，j=1，2，…，9。购房决策的5个备选方案对总目标购房的权重计算公式为：

(2)评价购房模型的层次总排序计算以及数据的一致性检验，计算公式如下：

CI表示B层次中判断矩阵的一致性指标，RI表示B层次中判断矩阵的随机一致性指标。

CR=CI/RI

当数值CR<0.1的条件下，购房模型的层次总排序是正确的，层次总排序的数据一致性可以接受，据此选择最终得到最佳购房方案。

3　案例分析

3.1选择购房城市

以山东省济南市为例进行购房决策分析。假设在济南市市中区、历城区、历下区、槐荫区和长清区进行房源选择，利用层次分析法分析得出最终的最佳方案，准确地进行购房决策。

3.2建立购房模型

针对购房考虑的房价、户型、升值、子女教育、医疗、超市配置、交通情况、居住环境和地理位置9个因素，在市中区、历下区、历城区、槐荫区和长清区进行购房决策，建立模型，如图1所示。

3.3中间层要素对最高层购房决策目标的单层次权重系数计算及其一致性检验

3.3.1中间层要素对最高层购房决策目标的权重系数计算

(1)搜集中间层要素信息及其量化要素。在“问卷网”上有针对性地投放调查问卷500份，搜集济南市房地产信息以及市民购房决策时对房价、户型、升值、子女教育、医疗、超市配置、交通情况、环境、地理位置9个购房因素的考虑情况。统计并分析所收集的数据，然后结合表2判断矩阵因子的赋值标准进行分析，得到的结果如表3所示。

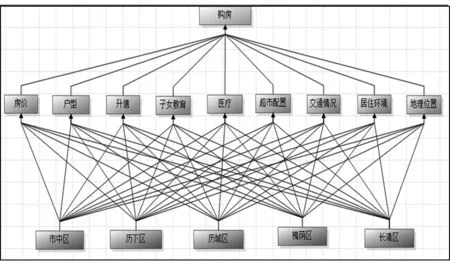
图1　购房的递阶层次结构

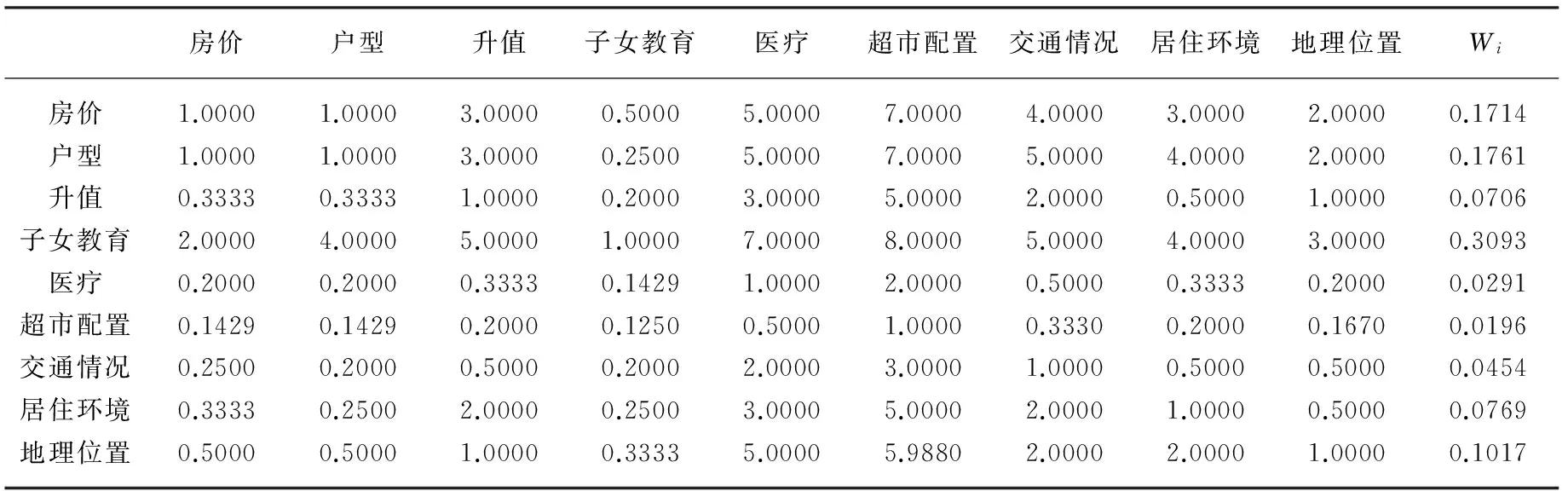
房价户型升值子女教育医疗超市配置交通情况居住环境地理位置Wi房价1.00001.00003.00000.50005.00007.00004.00003.00002.00000.1714户型1.00001.00003.00000.25005.00007.00005.00004.00002.00000.1761升值0.33330.33331.00000.20003.00005.00002.00000.50001.00000.0706子女教育2.00004.00005.00001.00007.00008.00005.00004.00003.00000.3093医疗0.20000.20000.33330.14291.00002.00000.50000.33330.20000.0291超市配置0.14290.14290.20000.12500.50001.00000.33300.20000.16700.0196交通情况0.25000.20000.50000.20002.00003.00001.00000.50000.50000.0454居住环境0.33330.25002.00000.25003.00005.00002.00001.00000.50000.0769地理位置0.50000.50001.00000.33335.00005.98802.00002.00001.00000.1017

注：Wi值为计算所得，其他表格数据为问卷调查所得。

(2)利用和方法进行权重系数计算。

3.3.2中间层要素对最高层购房目标决策的一致性检验

λmax=1/9×(1.613/0.1714+1.6573/0.1761+0.6645/0.0706+2.9097/0.3093+0.2742/0.0291+0.1841/0.0196+0.427/0.0454+0.7236/0.0769+0.9566/0.1017)=9.4080

(2)计算一致性指标：

CI=(λmax-n)/(n-1)

=(9.4080-9)/(9-1)

=0.051

(3)查询表2得相应的平均随机一致性指标RI=1.46

(4)计算一致性比值：

CR=0.051/1.46=0.0349

因为0.0349<0.10，所以认为判断矩阵的一致性是可以接受的,得到最终的数据如表3所示。

购房因素：λmax=9.4080，一致性指标CI=0.0510，购房一致性比值CR=0.0349。

3.4方案层对中间层的权重系数计算及其一致性检验

(1)根据问卷调查数据，结合专家经验评定，得到房价决策的两两比较判断矩阵数据，结果如表4所示。

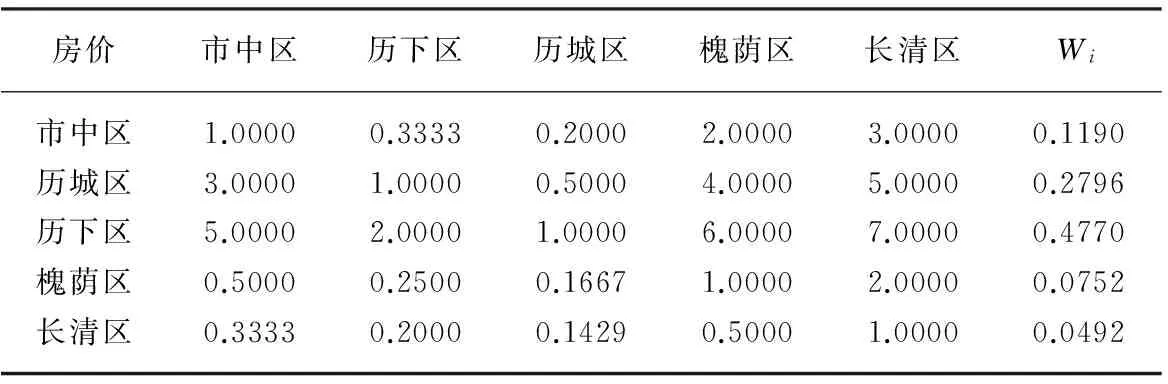
表4　方案层对房价的权重系数

(2)利用和方法计算方案层对房价的相对权重系数，可得：购房因素λmax=5.0883，一致性指标CI=0.0221，购房一致性比值CR=0.00197。

同理可得方案层对中间层的权重系数(表5)。

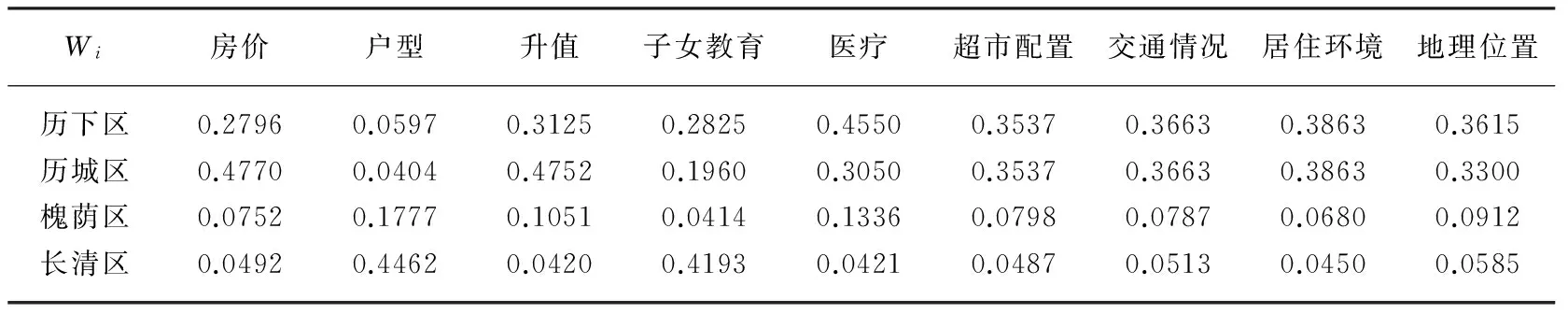
表5　方案层对中间层的权重系数

3.5购房决策层次总排序

3.5.1计算购房因素总权重

根据总权重计算公式:

市中区总权重：

Wi=0.1714×0.119+0.1761×0.276

+0.0706×0.0653+0.3093×0.0608

+0.0291×0.0643+0.0196×0.1641

+0.0454×0.1374+0.0769×0.1144

+0.1017×0.1589=0.1287

同理可得历城区总权重、历下区总权重、槐荫区总权重、长清区总权重依次为0.2711、0.2787、0.0879、0.2336。

3.5.2购房总权重一致性检验

CI=0.1714×0.0197+0.1761×0.0206

+0.0706×0.0200+0.3093×0.0190

+0.0291×0.0337+0.0196×0.0043

+0.0454×0.0090+0.0769×0.0127

+0.1017×0.0111=0.0179

RI=0.1714×1.12+0.1761×1.12

+0.0706×1.12+0.3093×1.12+0.0291

×1.12+0.0196×1.12+0.0454×1.12

+0.0769×1.12+0.1017×1.12=1.0123

CR为一致性比值，计算公式为：CR=CI/RI=0.0179/1.0123=0.177，因为0.0177<0.10，所以认为判断矩阵的一致性是可以接受的。

综上所述，最终购房决策因素的总权重数据如表6所示。

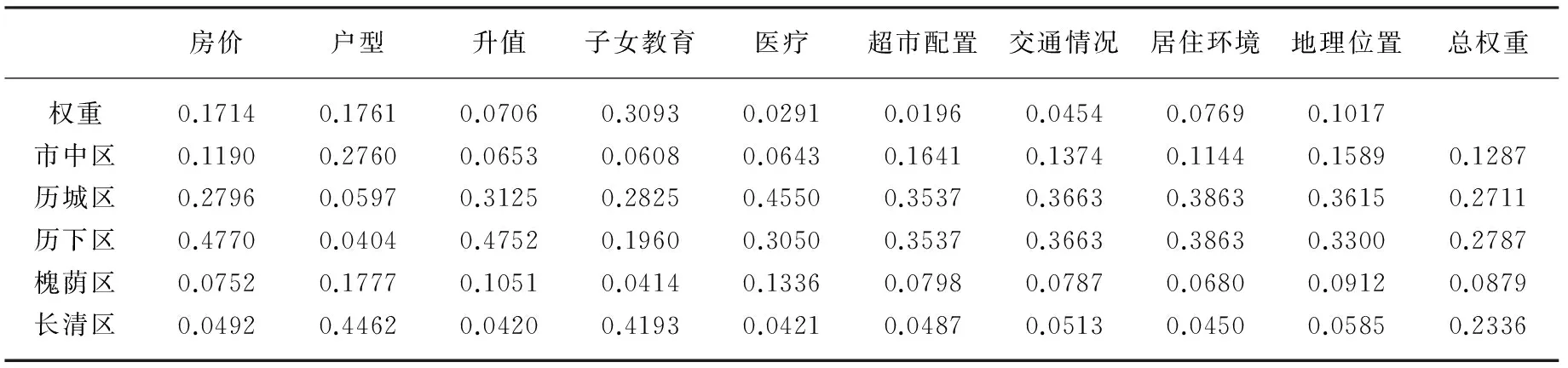
表6　购房因素的总权重系数

4　结束语

表6显示，市中区、历城区、历下区、槐荫区、长清区的总权重依次为0.1287、0.2711、0.2787、0.0879、0.2336，比较数值大小可知，0.2787>0.2711>0.2336>0.1287>0.0879,所以济南购房的排序为：历下区>历城区>长清区>市中区>槐荫区，即历下区住房性价比最高，其次是历城区、长清区和市中区，槐荫区最差，消费者购房决策时可优先选择历下区。

这个决策结果符合济南市区的购房实际情况。不过以上结论是消费者高度重视教育指标的结果。由于对子女教育的重视，市民购房时首选学区房，反映在购房判断矩阵上就是子女教育指标权重大于其他购房指标。长清区拥有大学城，房价较低，也是相对较好的选择。历城区权重(0.2711)略低于历下区(0.2787)，但相差无几，两个区的房价、环境、超市等配置也基本相当，建议把历城区作为备选方案。

[1]陈伟.正确认识层次分析法(AHP法)[J].人类工效学,2000,6(2):32-35

[2]陈江涛.论情境因素对消费者购房决策的影响[J].消费经济,2005(1):86-89

[3]李宏勋,丁鹏.房地产市场进化博弈与消费者购买决策[J].甘肃科学学报,2015,27(2):118-123

[4]丁香乾,石硕.层次分析法在项目风险管理中的应用[J].中国海洋大学学报:自然科学版,2004,34(1):97-102

[5]赵焕臣.层次分析法[M].北京：科学出版社，1986:5-8

[6]李崧,邱微,赵庆良.层次分析法应用于黑龙江省生态环境质量评价研究[J].环境科学,2006,27(5):103-104

[7]曲大义,王炜,邓卫.层次分析法在公路网规划建设项目排序中的应用[J].公路交通科技,2000,17(5):102-106

[8]丁香乾,石硕.层次分析法在项目风险管理中的应用[J].中国海洋大学学报：自然科学版,2004,34(1):97-102

[9]王以彭,李结松.层次分析法在确定评价指标权重系数中的应用[J].南方医科大学学报,1999,19(4):377-379

[10]喻良,伊武军.层次分析法在城市生态环境质量评价中的应用[J].四川环境,2002,21(4):38-40

(责任编辑：周博)

10.3969/j.issn.1673-2006.2016.10.009

2016-03-31

李天赐(1990-)，山东郯城人，在读硕士研究生，主要研究方向：工业工程管理。

C934

A

1673-2006(2016)10-0036-05