数字移相法测量无功功率的一种改进方法

张 凯，唐戈彦

（湖南省电力公司东江水力发电厂，湖南 资兴 423403）

数字移相法测量无功功率的一种改进方法

张 凯，唐戈彦

（湖南省电力公司东江水力发电厂，湖南 资兴 423403）

无功功率测量在电力系统中具有非常重要的作用。针对传统数字移相法测量无功功率存在的不足，提出了一种改进方法，该方法首先构造一个FIR数字滤波器，同时根据当前频率计算将电压移相1/4周期需要平移的采样点数以及需要补偿的角度，然后通过构造的滤波器对经过采样点平移的电压进行移相，使电压准确移相90°，接着将移相后的电压采样值和电流采样点值进行点积计算瞬时功率，最后通过求该瞬时功率的周期平均值计算无功功率。本方法中FIR数字滤波器的参数预先做成表格，实际补偿时可通过查表获取相关参数，因而算法的实时性高，易于程序实现。实际应用结果表明，改进方法测量无功功率的效果明显优于传统数字移相法，且不受输入信号频率变化的影响。

无功功率测量；数字移相；FIR数字滤波器；角度补偿

0 引言

电力系统运行时，电网需要提供两部分电能：用于单向转换成其他能量的有功功率和用于电磁场能量交换的无功功率。无功功率对供电系统和负荷的正常运行非常重要，但是，无功功率在电网中流动会引起供电电压变化和输电网络损耗。因此，无功功率测量已成为电力系统中必不可少的环节，在发电厂进行无功调节更是不可或缺，这对提高电能利用效率和节约能源具有重要意义。而无功功率测量尤其是准确、实时、高效的测量一直是个难题。

目前，常用的无功测量方法主要有功率三角法、数字移相法、FFT法、Hilbert滤波器法、小波变换法、神经网络法等［1-5］。但这些测量方法均没有同时在准确度、实时性上达到最佳，都存在一定的局限性，如功率三角法求出的无功功率不具有方向性，失去了无功功率象限信息；数字移相法测量无功实现简单、准确度好、实时性强，但在信号频率变化时会出现移相误差，虽可通过软件同步采样方法来减小误差，但以牺牲实时性为代价；FFT和Hilbert滤波器法可得到较好的测量结果，但FFT计算量大且程序实现复杂，Hilbert滤波器设计较困难，同时两种方法对硬件性能要求非常高，一般需要高性能数字信号处理器来实现；另外，小波变换和神经网络算法复杂，计算量大，耗时长，工程实用化很难。

因数字移相法测量无功的方法简单、实时性强、测量精度较高，且实施成本低，目前大多数电能计量仪表采用的仍然是这种方法，即把电压移相1/4信号周期后与电流点乘并累计，通过计算电压电流点乘的周期平均值即可求出无功功率［6-8］。

针对传统数字移相法测量无功存在信号频率变化及是否同步采样会影响测量准确度的不足，本文提出了一种改进算法。该算法通过构造一个FIR数字滤波器产生小数相移，对经过整数个采样点平移的电压进行小数移相补偿，使电压准确移相90°，然后再计算瞬时无功功率，最后通过计算该瞬时无功功率的均值求出无功功率。采用改进数字移相算法测量无功的准确度明显优于传统数字移相法，且不受信号频率变化的影响。

1 数字移相法原理

设在正弦电路中电压、电流的瞬时值表达式分别为：

则瞬时功率p（t）为：

可见，瞬时功率中包含两部分内容：瞬时有功功率Pp（t）和瞬时无功功率Pq（t）。

由（3）式可知，瞬时有功功率Pp（t）在一个周期内的均值与瞬时功率P（t）在一个周期内的均值是一致的，而瞬时无功功率Pq（t）的均值为零，因而不能直接通过计算瞬时功率均值的方法来求出无功功率Q。然而，瞬时有功与瞬时功率的关系可通过将（3）式中电压u（t）或电流i（t）进行正余弦变换而调换，即变为瞬时无功功率Pq（t）在一个周期内的均值与变换后的瞬时功率P（t）在一个周期内的均值是一致的，而变换后的瞬时有功功率Pp（t）的均值为零，此时即可通过计算瞬时功率均值来求出无功功率。根据正弦余弦之间转换关系sinφ=cos（90°-φ），可将电压波形u（t）移相90°进行正余弦变换，然后再同电流i（t）相乘，此时瞬时无功功率的均值与瞬时功率的均值一致，从而可以通过计算此时瞬时功率的均值来求出无功功率。

移相后的瞬时功率P'（t）为：

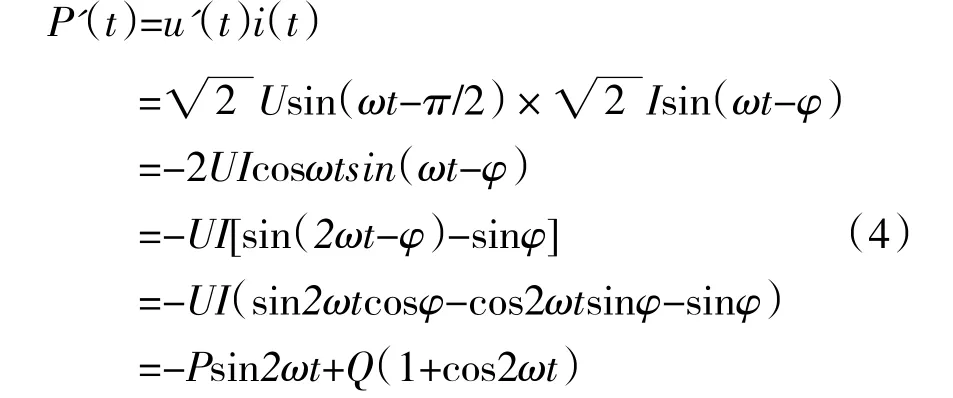
根据（4）式，可以得到无功功率的计算公式为：

把上式写成离散形式：

其中：Q表示无功功率，N为每周期的采样点数，u（k）和i（k）分别为电压和电流的第k个采样点值。

以上（5）式和（6）式即为数字移相法测量无功的基本原理。由（6）式不难看出，当每个周期的采样点数不是整数或N/4不是整数，则会产生移相误差，进而产生无功测量误差。即使在标称信号频率下能满足N/4是整数的条件，然而当信号频率变化时也同样会产生较大的误差。目前可采取如下几种方法来减小误差：①采用PLL倍频技术，使采样频率一直为信号频率的4n倍，然而增加了硬件投入，且锁相倍频电路复杂；②采用软件准同步方法，精度非常高，但测量实时性大大降低。

2 改进的数字移相法

2.1 改进算法原理

针对传统数字移相法测量无功功率存在的不足，本文提出了一种改进的数字移相算法，即当电压移相的1/4信号周期不是采样间隔的整数倍时，采用FIR数字滤波器产生小数相移，对经过整数个采样点平移的电压进行小数移相补偿，使电压准确移相90°，从而实现无功功率的准确测量。

改进算法实现无功准确测量的基本原理为：

（1）实时测量输入信号频率，由新的信号频率fm计算周期点数N=fs/fm（其中fs为采样频率，N包括小数部分），同时改变无功计算时的电压移相值N/4；

（2）将电压移相分成整数移相（对应移相值整数部分）和小数移相（对应移相值小数部分）两部分，整数移相通过直接对电压平移整数个采样点实现，平移的采样点数即为移相值fs/（4fm）的整数部分［fs/（4fm）］，而小数移相则通过采用FIR数字滤波器产生小数相移，对平移后的电压进行小数移相补偿实现；

（3）将移相后的电压与电流相乘计算瞬时无功功率，计算该瞬时无功功率的均值从而求出无功功率。

改进算法的关键在于采用FIR滤波器产生小数相移，对经过整数个采样点平移的电压进行小数部分移相补偿，使电压移相达到精确的90°，其中待补偿的小数部分相位△φ与当前信号频率fm的关系为：

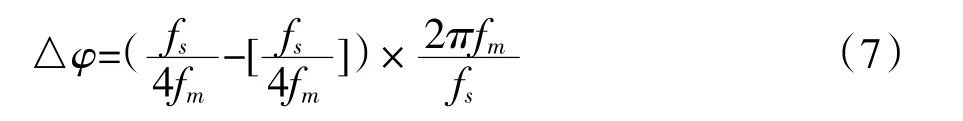
其中：fs为采样频率，［fs/（4fm）］表示fs/（4fm）的整数部分。

2.2 FIR数字滤波器设计

FIR数字滤波器具有稳定性好、具有线性相位特性等优点，是实现小数移相最简单有效的方法。为实现上述小数移相，可以通过一阶单零点FIR滤波器来实现，其差分方程和原理框图分别如下所示：

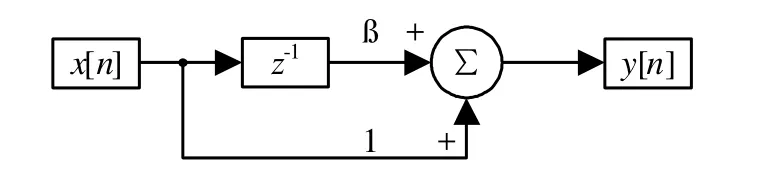
图1 一阶单零点FIR滤波器原理框图

其中：x是输入电压，y是延迟后的输出电压，n是采样序列，β是延迟增益。

对（8）式两边进行归一化Z变换，则FIR滤波器的系统函数为H（z）=Y（z）/X（z）=1+βz-1。由于FIR的冲激响应是有限长的，则可以实现严格的线性相位。令z=ejω，这里ω为数字角频率（ω=2πfm/fs），则系统函数的频率响应为：

根据频率响应得到FIR滤波器群延迟为：

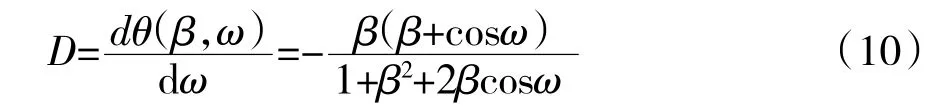
由上式可以解出延迟增益β为：

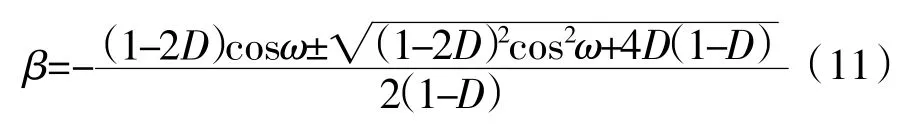
其中D的求解，可依据群延迟的物理意义，其与待补偿的小数部分相位△φ的关系为：

由于FIR滤波器存在非归一化增益，相位补偿后电压幅度增加，且受频率影响，为简化计算过程，在最后计算瞬时无功功率均值时进行比差补偿，实际补偿时乘以滤波器增益的倒数，即：

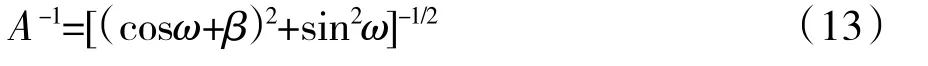
2.3 建立FIR滤波器参数表

由以上滤波器设计可知，求无功功率之前需要计算FIR滤波器的延迟增益β和无功功率的增益补偿系数A-1，这两个参数可分别由（11）式和（13）式计算得到。由于（11）式和（13）式的计算过程较复杂，为简化算法执行时的计算量，根据补偿相位值与滤波器延迟增益和无功功率增益补偿系数的对应关系，建立FIR数字滤波器的参数表，实际补偿时根据需要补偿的小数相位，查询该参数表获取FIR滤波器的参数。下面对参数表建立的具体过程进行说明：

（1）确立参数表需要支持的移相范围。根据（12）式，可知群延迟D的取值范围为［0，1），因此参数表必须支持最大一个采样角的移相，即参数表需要满足移相范围 ［0，△φm），其中△φm为最大移相角度，△φm=2π fm/fs。

（2）确立参数表的大小。根据需要达到的移相分辨率δ和最大移相角度△φm确立参数表的大小M，M取值应满足△φm/M≤δ，实际应用中M一般取128。

（3）建立参数表索引与延迟增益β和无功功率增益补偿系数A-1之间的对应关系。参数表索引r依次取值0，1，2，…，M-2，M-1，其对应的移相角度依次为0，△φm/M，2△φm/M，…，（M-2）△φm/M，（M-1）△φm/M，然后每一个移相角度对应一个延迟增益β和一个无功功率增益补偿系数A-1，即每一个表索引对应一个β和一个A-1参数。

（4）计算每个表索引对应的β和A-1参数值并存入相应的索引位置，具体如下：

1）根据采样频率fs、信号频率fm和公式ω=2π fm/fs，计算得出数字角频率ω；

2）根据每个表索引r对应的移相角度△φr=r△φm/M和公式（12），计算得到群延迟D的值，D=△φr/ω=r△φm/（Mω）；

3）将计算得到的ω和D代入公式（11）和（13），得出β、A-1的参数值；

4）为了方便计算，将β、A-1转化成16位有符号整型数据，为两参数选取计算量纲，所计算的数值乘以各自量纲；

5）将所得β、A-1参数存入参数表。

2.4 基于改进移相法的无功测量

基于上述所构造的FIR数字滤波器，前文（6）式描述的数字移相法测量无功的计算公式则相应地改为：

其中：Q表示计算得到的无功功率；A-1是无功功率的增益补偿系数，由（13）式计算得到；N是每个周期内的采样点数，N=［fs/fm］（［fs/fm］表示对fs/fm取整）；u（k）和i（k）分别为电压和电流的第k个采样点值；β是FIR滤波器的延迟增益，由（11）式计算得到；［fs/（4fm）］表示对fs/（4fm）取整。

3 实验结果

该无功测量方法已应用于本厂电能计量仪表上，并且对其进行了基本误差试验和频率影响量试验。基本误差试验电流点为0.005 Ib、0.01 Ib、0.02 Ib、0.05 Ib、0.1 Ib、0.2 Ib、0.5 Ib、Ib、0.5 Imax、Imax（Ib为基本电流，Ib=5 A，Imax为最大电流，Imax=60 A），每个试验电流点分别测试了1.0，0.5L、0.8C功率因数的误差；在频率影响量试验中，测试频率为45Hz、50Hz、55 Hz、60 Hz、65 Hz，每个试验频率点分别测试1.0，0.5L，0.8C功率因数的误差。基本误差和频率影响量的测试结果分别如图2和表1所示。

从测试结果可以看出，改进方法具有良好的无功测量精度，且基本不受频率变化的影响。

图2 基本误差实验结果

表1 频率影响量实验结果

4 总结

本文提出采用FIR数字滤波器对无功移相1/4周期进行小数部分相位补偿，使数字移相达到精确90°，从而实现无功的高准确测量，该方法弥补了传统数字移相法测量无功功率受频率变化及是否同步采样影响严重的问题。与传统数字移相法测量无功相比，改进移相算法测量无功的准确度高，且基本不受频率变化的影响。同时，FIR数字滤波器的参数预先计算好并做成表格，实际补偿时通过查表获取对应参数，这大大简化了算法执行时的计算过程，有效提高了算法的执行效率。因此，该方法在高精度无功功率测量仪表的实际应用中具有一定的参考价值。

［1］高 朝.采用数字相移网络进行无功功率测量的研究［J］.计算机仿真，2006，23（7）：236-239.

［2］富致超，田春雨，耿心志，等.数字移相法测量无功功率的频率误差补偿［J］.电测与仪表，2004，41（10）：9-11.

［3］许春香，孙建延，胡春华，等.基于CS5460A设计三相电能表关键技术研究［J］.电测与仪表，2010，47（12）：49-52.

［4］庞 浩，王赞基，陈建业，等.基于2对Hilbert移相滤波器的无功功率测量方法［J］.电力系统自动化，2006，30（18）：45-48.

［5］王 薇，王晓茹，黄晓青，等.无功功率测量的Hilbert数字滤波器研究［J］.电测与仪表，2007，44（3）：9-12，37.

［6］郑常宝，王群京，郑长勇，等.用小波包测量无功功率［J］.系统仿真学报，2006，18（7）：1902-1905.

［7］肖皓皓，王学伟，王 琳，等.小波滤波器组功率测量方法的分析［J］.电测与仪表，2006，43（1）：4-8.

［8］孙爱平，林世治.无功功率测量分析［J］.电气自动化，2014（5）：65-66，106.

［9］富致超，王伦展，耿心志，等.积分法测量无功功率的原理初探［J］.电测与仪表，2004，41（3）：1-2.

［10］TEXASINSTRUMENTSINCORPORATED.MSP430F67 3X/MSP430F6 72X Mixed SignalMicrocontroller Datasheet［Z］.2011.

［11］宋慧娜，易龙强.一种高精度动态角差补偿算法［J］.电测与仪表，2010，47（12）：12-15.

［12］杨 林，王 猛.无功计量标准装置的建立及量值比对［J］.电测与仪表，2012，49（3）：33-35.

TM933.3+7

A

1672-5387（2016）07-0016-04

10.13599/j.cnki.11-5130.2016.07.005

2016-05-16

张 凯（1982-），男，工程师，从事水电厂自动化专业技术管理相关工作。