基于ARIMA-MC模型钢铁企业高炉煤气发生量预测

熊文真　赵娜

（信阳职业技术学院　河南信阳464000）

节能减排与综合利用

基于ARIMA-MC模型钢铁企业高炉煤气发生量预测

熊文真赵娜

（信阳职业技术学院河南信阳464000）

为了预测钢铁企业高炉煤气发生量，本文用ARIMA模型及马尔科夫链建立了ARIMA-MC模型对高炉煤气的发生量进行预测。结合某钢铁企业实际的原始数据 ，通过实验，随机抽取多组测试结果中的两组，1#和2#各30个点进行预测，结果表明预测平均相对误差分别为2.27%、3.03%。实验结果证明新算法的有效性。

高炉煤气发生量 ARIMA模型 ARIMA-MC模型 马尔科夫链

0　引言

高炉煤气（BFG）是钢铁企业的重要二次能源之一，大型企业在生产钢铁过程中，为了保证其正常运行，高炉煤气发生量的变化趋势需要随时准确掌握。因为在实际生产过程中，影响分配高炉煤气的因素复杂，原始数据的周期波动变化较大以及大量随机的人为扰动现象，有效的预测模型［1-2］较难建立，高炉煤气能否供需平衡、回收利用的程度，直接影响钢铁企业的生产成本，因此高炉煤气的发生量预测对企业节能降耗有重要意义［3］。国内外专家通常采用时间序列、回归分析、神经网络等方法［4］推测高炉煤气的发展趋势、水平和程度等，其中时间序列预测大多采用简单滑动预测。研究时间序列的重要方法之一便是ARIMA模型，ARIMA模型先根据高炉煤气的特点识别模型，试用此模型，然后对所选试用模型反复加以诊断，反复做出相应调整，直到选择适合的模型。由于高炉煤气发生特性，单纯依靠ARIMA模型进行预测会存在当工况改变时预测效果不佳，本文先用ARIMA模型对高炉煤气发生量进行预测找出变化趋势，然后在ARIMA模型预测的基础上再用马尔科夫链对其修正，此方法称为ARIMA-MC。

1　ARIMA-MC模型建立

对钢铁企业的实际数据进行反复试验后得出，假设直接对原始数据采用ARIMA模型预测，对有波动噪声的数据预测性会因为模型缺乏稀疏性和鲁棒性而预测精度低。理论能够预测随机变化的动态系统，其转移概率能够比较准确的反映钢铁企业各种随机因素的影响程度，缩小预测数据的区间，能够很好的对数据进行长期预测，除此之外马尔科夫链还能够根据数据状态之间的转移概率高低推测系统未来的发展方向，对于随机波动较大的数据序列预测效果也不错，但它的缺点是，要求要预测的数据具有平稳的均值特性、状态无后效性等。基于此情况，本文先利用ARIMA模型对要预测的模型预测出其变化趋势，再用马尔科夫链对其修正，这样能够弥补马尔科夫链预测的局限性，提高了ARIMA模型对随机波动大的数据序列的预测效果。

1.1ARIMA模型

ARIMA模型可表示为［5］：

式中，p是描述自回归阶数，q是移动平均阶数，d是以及差分次数 ，Zt为原序列，at是随机变量白噪声序列（互之间无关、其均值为0、方差为 σ2），B为BZt=Zt-1（后移算子），φp自回归因子，φp（B）=（1 -φ1B-…φpBp），p为模型的自回归阶数；θq为移动平均算子，θq（B）=（1-θ1B-…θqBq），q为模型的移动平均阶数；θ0为参数，μ为平均数，θ0=μ（1 -φ1-φ2-…-φp）。

1.2 基于MC修正的ARIMA建模

马尔科夫链预测数据的基本步骤为：

（1）确定系统状态。由于许多人为因素干预，预测状态没有事先被划定 ，预测没有统一标准。而本文中对明确确定的煤气量的预测系统状态，分为三类状态，分别为：上升、平稳、下降。

（2）计算初始概率。设被预测的煤气发生量的时间序列取值区域为 X，X被划分为r个集合，E1，E2，…，Er。时间序列 x1，x2，…，xn可以观测得到，其中最后一个时刻观测值 xn，由于不确定 n时刻后的转移状态 ，即不知道 xn的取值，可以先不考虑xn。假设在前 n-1个观测序列的数据中，其中落在状态 Ei中有Mi，则∑Mi=n-1。状态 Ei发生的频率为

令 Pi=Fi作为系统状态Ei发生的初始概率。

（3）计算一步转移概率矩阵。设有 Mi个观测时间序列｛xt，t∈T｝处于 Ei状态式中 ，Mij个数据在其下一时刻转移到状态Ej。取

式（3）是要预测的数据从 Ei状态转移到下一时刻Ej状态的转移概率，由此可以得到预测数据的一步转移概率矩阵 P。

（4）利用由上述步骤得到的一步转移概率矩阵P对煤气发生量的数据预测。假设时间序列观测值落入状态 Ei中，P的第i行元素为：

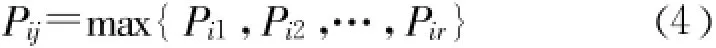
则xt+1=将会转移到状态 Ej的可能性最大，而转移到其他状态的概率比较小［6］。

2 模型应用

以某钢铁企业为例，用本文所建模型对高炉煤气进行预测，数据每30 min采集一次，period表示时间间隔。

2.1 序列平稳性的判断

由于对高炉煤气原数据序列进行检查的结果发现原数据序列并不平稳。对这些不稳定的原数据进行一阶差分后得到新序列，然后对新序列作ADF检验，结果如表1所示，单位根统计量ADF=-16.314 31（明显小于EVIEWS给出的临界值），可以推出原假设正确，得到的新序列是平稳的。

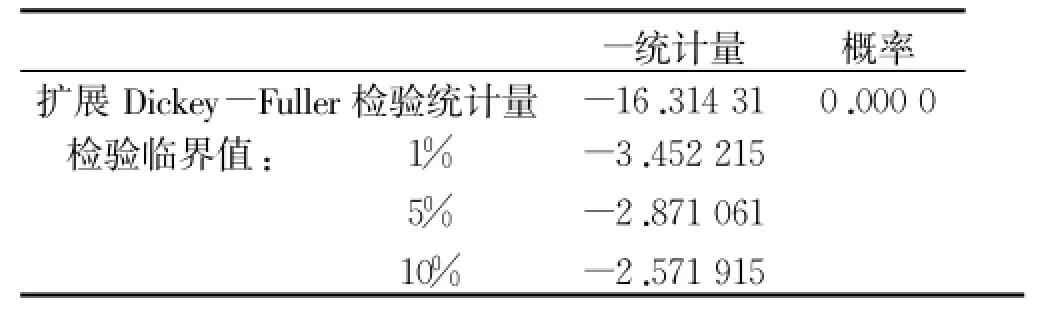
表1数据平稳性检验

2.2 模型识别及参数估计（见表2和表3）

表2模型参数估计

表3模型系数

由上述各表分析得出，高炉煤气发生量数据的残差为白噪声模型，在数据信息提取中；模型参数既显著又精简，因此建立ARIMA（3，1，1）模型对本文高炉煤气发生量进行预测。

2.3基于ARIMA-MC模型的预测

通过以上高炉煤气数据的分析，发现ARIMA（3，1，1）模型可以较好的对其预测，进而得到ARIMA-MC模型预测值。在预测过程中，对ARIMAMC与ARIMA两个模型方法进行比较，利用eviews进行计算，由高炉煤气发生量预测结果对比图1、图2可知，本文所建模型ARIMA-MC的预测效果比较理想，从两个图中可以看出，本文所建预测模型ARIMA-MC预测精度较高，可以实时跟踪高炉煤气发生量的变化趋势，当预测数据比较平稳的情况下，ARIMA-MC与ARIMA两种预测方法精度相差不大，如果预测数据发生变化时，本文采用的方法ARIMA-MC预测效果明显好于ARIMA的预测效果，本文预测方法的建立对钢铁企业的生产有重要的指导意义。由表4也可以看出，利用本文提出的ARIMA-MC模型对1#高炉和2#高炉煤气发生量的预测 ，其平均绝对误差（MAE）分别为9.25、12.45；平均相对误差（MPE）分别为 2.27%、3.03%，其MAE、MPE明显小于ARIMA模型。因此利用本文所建ARIMA-MC模型对高炉煤气发生量进行的预测效果比较理想。

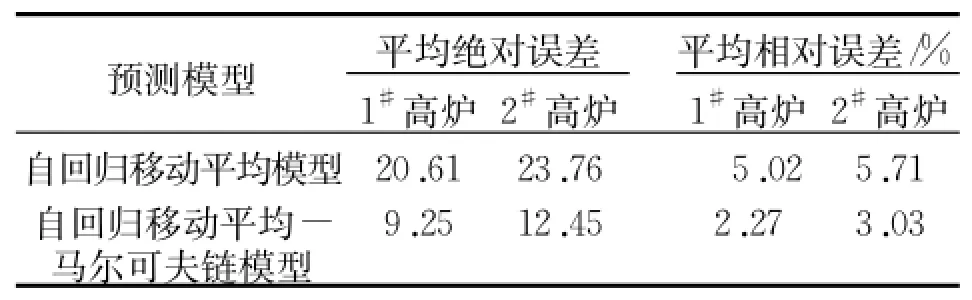
表4　实际值与预测值对比

图1　1#高炉煤气发生量

图2　2#高炉煤气发生量

3　结语

本文充分考虑到副产煤气发生量的周期波动幅度较大这种不平衡性，提出了一种新的方法对钢铁企业高炉煤气发生量进行建模预测，与ARIMA模型预测相比，ARIMA-MC模型预测精度高。利用钢铁企业实际生产数据进行验证，两个模型随机选取的预测平均相对误差分别为2.27%、3.03%，实验结果证明本文算法具有良好的预测性能。

［1］张琦，蔡九菊，王建军，等.钢铁厂煤气资源的回收与利用［J］.钢铁，2009，43（12）：95-99.

［3］刘渺.钢铁企业主工序分厂煤气量预测方法研究［D］.长沙：中南大学，2006.

［4］郑莉，段冬梅，陆凤彬，许伟，杨翠红，汪寿阳.我国猪肉消费需求量集成预测——基于ARIMA、VAR和VEC模型的实证［J］.系统工程理论与实践，2013，4（33）：918-925.

［5］岳有军，户彦飞，赵辉，王红君.基于小波分析的ARIMA与LSSVM组合的高炉煤气预测［J］.计算机测量与控制，2015，23（6）：2128-2131.

［6］郭坤卿，马永红，王涛峰，孙立勇.基于改进灰色-马尔可夫链方法的铁路货运量预测［J］.兰州交通大学学报，2009，28（6）：131-133.

Prediction of Blast Furnace Gas in Iron and Steel Enterprises Based on ARIMA-MC Model

XIONG Wenzhen ZHAO Na
（Xinyang Vocational&Technical College Xinyang，Henan 464000）

In order to predict blastfurnace gas from iron and steelenterprises，ARIMA-MC Modelis established based on ARIMA model and Markov chain to predict the blast furnace gas occurrence.In accordance with the primary data from one iron and steel enterprise，two groups in several groups of test resluts are randomly selected to carry out prediction for blast furnace 1#and 2#in 30 prediction points and the average relative prediction errors are 2.27%and 3.03%respectively. The experimental results show the effectiveness of the algorithm.

blastfurnace gas output ARIMA model ARIMA-MC model Markov chain

熊文真 ，女，硕士 ，讲师，研究方向：数学建模、数字图像处理。

（2015-12-25）