在图形与几何教学中培养迁移能力

浙江宁波市鄞州区下应街道中心小学（315104）　俞孟立

在图形与几何教学中培养迁移能力

浙江宁波市鄞州区下应街道中心小学（315104）俞孟立

几何图形间都存在着非常紧密的联系，如果单独对一块知识点组织教学，割裂了知识点之间的联系，会造成学生对概念的认识片面化，不利于学生学习能力的培养。教师如果能根据几何图形间的内在联系巧妙组织教学，就能有效培养学生的知识迁移能力。

几何图形知识迁移类比对比举一反三

知识迁移是“一种学习对另一种学习的影响”，是根据自身的经验背景，对外部信息进行主动地选择、加工和处理等过程。在图形与几何的课堂教学中充分运用迁移规律，实现知识的有效迁移，是教学成功的一个重要环节。学生形成较好的知识迁移能力后，可以避免死记硬背，实现知识点之间的贯通理解和转换，有助于认识事物的本质和规律，从而构建知识结构网络，提高解决问题的灵活性和有效性。

一、加强联系，以类比促迁移，实现迁移通畅

知识迁移的产生与前后知识之间的相同因素和相互关系有关。只有找出新旧知识的内在联系，学生才能将知识进行迁移。因此，教师在教学中要引导学生对已经学习过的知识进行回顾和总结，找出两者的内在联系，使学生可以自主地链接新旧知识，引导学生由此及彼，以旧学新，突破难点，掌握新知。

如教学“三角形的高”时，可以平行四边形的高为桥梁，通过类比，顺势关联新知。

【镜头重现：三角形高的定义及作高】

1.出示平行四边形。利用课件动态演示平行四边形到梯形再到三角形和三角形到梯形到平行四边形的变化过程。

①复习平行四边形的高，课件演示作高的过程，让学生拿起尺子跟着电脑一起作高，教师在一旁提示：“一条直角边与底重合，另一条直角边为过某个点的垂线。”

②给出概念：从平行四边形一条边上的一点到对边引一条垂线，这个点和垂足之间的线段叫做平行四边形的高，垂足所在的边叫做平行四边形的底。

③在平行四边形的一条边上取一点与其对边的两个端点连成三角形。如果以此边为底，三角形的高应该怎么画？

④你觉得三角形的高指的是什么？根据刚才的研究，三角形有三个顶点、三条边，可以画几条高？

2.迁移引导：你能不能根据平行四边形高的定义，类推出三角形高的定义？

3.概括高的意义：点到对边的垂线段。

在学习三角形的高之前，学生已经认识了三角形，通过变一变，动态中促进了平行四边形、梯形、三角形在数学本质属性上的联系。打通图形之间的联系，使学生意识到高并不是新事物，而是原先学过的旧知，用这样的“似曾相识”类推出三角形画高的方法。这样以类比促迁移，以旧学新，突破难点，学生不仅顺利掌握了新知，而且培养了知识迁移的能力。

二、辨析异同，以对比促迁移，克服思维定式

思维定式是指先于一定活动而指向该活动的一种准备状态。它有时会产生消极性影响，导致知识负迁移，从而影响学生理解和掌握知识。所以在发展迁移能力的过程中，要通过直观对比，把握各知识点的异同点。

如在教学“平行四边形面积”时，学生会受长方形面积计算方法的影响，出现负迁移。这就需要通过对比和动手操作去发现它们的不同点，消除消极影响，形成求异的意识与能力。

【镜头重现：平行四边形的面积】

师（出示教具）：这是一个长方形框架，它的长是7厘米，宽是5厘米，它的面积是多少？你是怎样思考的？

（复习长方形面积的计算方法，根据学生的回答，教师板书：长方形的面积=长×宽）

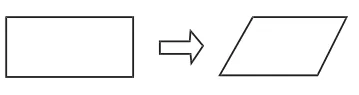
师：如果捏住这个长方形的3一组对角，向外拉（如右图），大家看看，它现在变成了什么图形？（平行四边形）

师：请你猜想一下平行四边形面积的计算公式。

（相当一部分学生受长方形面积计算方法的干扰，认为平行四边形的面积等于相邻两条边的乘积，但也有学生提出四边形的面积等于底乘高。）

师：究竟哪种猜想是正确的？下面利用手中的学具袋（袋中装有一个底是7厘米，邻边5厘米，高3厘米的平行四边形），小组合作，验证一下。

生A：长方形框架拉得越扁，面积就越小，所以平行四边形的面积等于相邻两条边的乘积是错误的。

生B：通过数格子，我发现平行四边形的面积等于底乘高。

生C：通过剪一剪、拼一拼，我发现平行四边形的面积等于底乘高。

当迁移能力发展到一定程度时，学生会出现思维定式，教师要及时地进行引导，通过对比等方法直观呈现，让学生克服定式思维。这要求学生对问题进行再处理、再变换，或尝试与另一认知结构对接，从不同角度分析、迁移知识解决问题，而不是生搬硬套。所以，具体问题要具体分析、具体处理，形成求异思维的意识与能力。

三、举一反三，以发散促迁移，实现迁移多元

迁移能使知识点构成一个有机的整体，在新旧知识间建立起实质性的联系，使新知识、新问题纳入到原有的认知结构中，形成知识网络。举一反三正是从“一”到“三”的发散过程，发现一类题的共性和表现形式，从而达到由会解这道题上升到会解这类题的境界。

如在教学长方形、正方形、平行四边形、梯形、三角形、圆的面积公式时，学生一般都采用单独记忆的方法，但如果通过迁移将这五种图形的面积公式概括为一个通用公式，就可以迅速将所有的公式记忆下来，减轻记忆的负担。

【镜头重现：平面图形面积的复习整理】

师（复习回顾）：我们学过哪些基本的平面图形？它们的面积计算公式是什么？用字母怎样表示？（生逐一回答，并说明公式中的字母各表示什么。）

师（梳理推导公式）：这些平面图形的面积计算公式之间有怎样的联系呢？

生：把长方形看成上底与下底相等的梯形，可用梯形面积公式推导长方形的面积公式：S=（a+a）×b÷2=2a× b÷2=ab。

师（举一反三）：梯形面积公式可推导出长方形的面积计算公式，你能用梯形面积公式推导出其他图形的面积计算公式吗？

（经过知识迁移，举一反三，学生很快发现正方形、长方形、梯形、三角形、圆形面积公式的共性：仍是面积等于上底与下底之和乘高除以2，如下图所示。）

（注：把圆看作上底为0，下底为周长，高为半径的梯形）

学生以长方形与梯形的面积计算公式间的联系为桥梁，通过举一反三，类推出其他平面图形的面积公式，实现知识的发散性迁移。经常进行这样的思维训练，学生就能将知识点灵活转换和应用，由会解这道题变为会解这类题，实现知识迁移能力多元化发展。

总之，在进行图形与几何的教学中，教师要经常让学生通过类比、对比、举一反三等活动充分运用迁移规律，实现知识的有效迁移。当学生较好的形成知识迁移能力后，可以实现知识点之间的贯通和转换，有利于认识事物的本质和规律，构建知识结构体系，提高解决问题的灵活性和有效性，形成并提升知识迁移能力。

（责编吴美玲）

G623.5

A

1007-9068（2016）29-068