一种改进的多波束卫星通信系统功率分配算法*

史 煜，张邦宁，郭道省，杨 柳

（解放军理工大学，江苏 南京 210007）

一种改进的多波束卫星通信系统功率分配算法*

史 煜，张邦宁，郭道省，杨 柳

（解放军理工大学，江苏 南京 210007）

对卫星通信系统进行合理的功率分配，可以提高功率资源的利用效率。针对多波束卫星通信系统功率分配中采用的迭代注水分配算法存在的实现复杂度高的问题，提出了一种改进的注水算法。该算法基于功率和波束容量受限的约束条件，利用Lagrange函数中每个波束的功率分配结果的非负对偶变量值相等建立等式，由一个波束的功率分配结果则可得到所有的波束功率分配结果，避免了功率分配过程中的迭代计算，从而有效降低了计算复杂度。仿真结果表明，在系统性能基本保持不变的条件下，该算法显著降低了运算复杂度。此外，探讨了系统误码率和波束数目对改进注水算法的影响。

多波束；功率分配；注水算法；复杂度；误码率

0　引 言

卫星多波束技术具有高增益、覆盖范围广、波束形状可灵活调整、频谱利用率高的优点，可以提高卫星的通信容量。然而，多波束卫星通信系统中功率资源非常宝贵，如何提高资源资源利用效率是多波束卫星通信系统亟待解决的问题。

目前，多波束卫星通信系统的功率分配问题已经受到了广泛关注，已有相关学者做了一些工作。文献［1］提出了一种考虑波束间干扰情况下，提升波束间资源分配公平性的动态功率分配算法，但是这种算法只有在某些特定场景下才能提升系统容量。文献［2］运用凸优化理论，同时考虑系统容量最大化和用户间的公平性，对多波束卫星系统的功率分配问题进行研究，结果表明算法复杂度取决于波束数目和用户数目，但是对具体的计算复杂度没有进行探讨和对比。文献［3］对Ka频段多波束卫星的功率分配进行了研究，主要降低了雨衰对系统的影响。文献［4］给出了一种在雨衰条件下，在服务地面固定终端的GEO卫星通信系统中，确保最多用户满足QoS的动态功率分配算法。文献［5］提出了对多波束中功率需求相近的用户进行分组，尽可能满足最多用户需求的功率分配算法。但是，文献［4］和文献［5］算法运算复杂程度较高，给计算带来了一定的难度。

本文针对多波束卫星通信系统，针对迭代注水算法计算复杂度高的问题，提出了一种改进算法，避免了传统算法的多次迭代计算，在尽量保证系统容量最大化的同时，降低了计算开销。

1　注水算法功率分配模型

本文对FDMA多波束卫星通信系统进行研究。在给定用户的可用功率后，功率该如何在各个波束上分配以确保整个系统的获取吞吐量最大化，是我们需要解决的问题。

设在FDMA多波束系统中有N个波束，第i个波束获得的容量为Ci，每个波束的带宽为B，第i个波束上的信道增益为αi，它的大小主要受天气条件、自由空间损耗和收发天线增益等条件的影响，第i个波束上的噪声功率谱密度为N0，i，第i个波束上分配的功率为Pi，Γ表示与物理层编码调制相关联的量。当传输中的误码率为BER，物理层的调制方式为MQAM与格雷编码联合时，Γ=-ln（5·BER）/1.5。为了方便表示，设定而Hi的大小体现了波束信道条件的好坏。

根据以上条件，系统获得的吞吐量为：

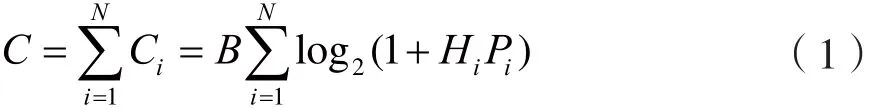
用迭代注水算法以系统吞吐量为优化目标分配功率，可以得到如下的数学模型：

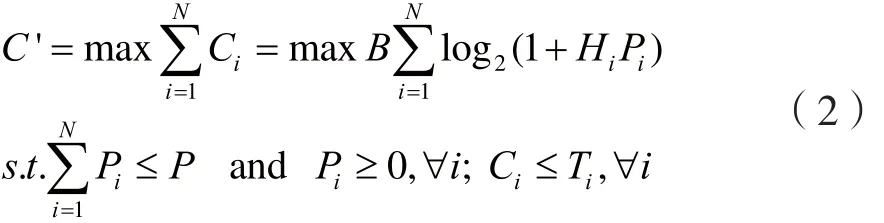
其中P表示系统总功率，Ti表示第i个波束的业务申请量，约束条件表示系统总的功率限制，约束条件表示一个波束上所获得的容量不得大于波束上的业务申请量，以防止浪费资源。

根据建立的数学模型，引入非负对偶变量λ和ρ=［ρ1，ρ2，…，ρi］，可以得到优化问题的Lagrange函数：

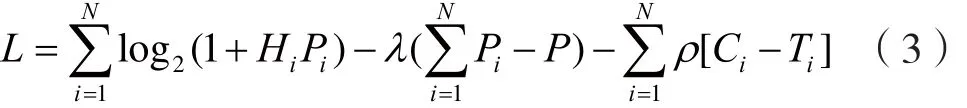
对L求关于Pi的偏导，令有：

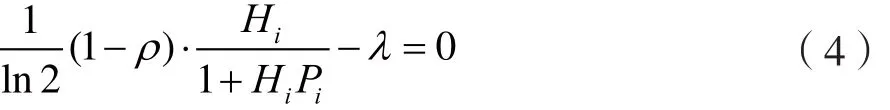
令β=λln2，有：

则可以算出：

其中［x］+=max｛0，x｝。此时还不能直接得到每个波束中分配的功率，对偶变量β和ρ需要经过更新迭代算法计算。在此，采用次梯度法更新对偶变量：

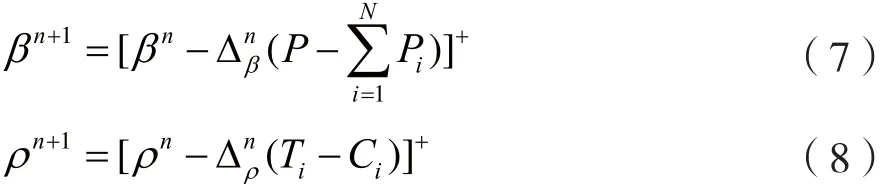
其中n表示迭代次数，Δ表示迭代步长。计算过程中，先将β和ρ的值初始化，再进行更新迭代计算，直到同时满足条件则算法终止，得到最终的β和ρ；否则，继续进行迭代计算。将最终计算结果β和ρ代入式（6），即可得到每个波束分配的功率。

在每次迭代计算过程中，需经过4N次加法运算和（2N+2）次乘法运算，整个算法的运算量为O（kN），其中N为波束的数目，k为采用次梯度法更新法进行迭代的次数。

2　改进的功率分配算法

采用线性算法进行功率分配时需要高SNR［8-9］，因为低SNR的波束会出现负值。在实际问题中，这些波束是不分配功率的。为了解决这个问题，这里提出一种避免多次迭代计算并且能够确定不分配功率的波束。

改进的功率分配算法：

由式（5）可知，对于同一个系统，β和ρ的值相同，则可得到：

其中m，i=｛1，2，…，N｝，则可以得到：

由式（10）可知，只要能确定一个波束分配的功率，就能确定其他波束上的功率。

所有波束分配的功率和为：

且Pm≥0∀m。当求出Pm＜0时，取Pm=0，则不满足的约束条件。因此，在迭代注水算法中，需要多次迭代计算得到适当的β和ρ值，以满足功率约束条件。

在改进注水算法中，先将波束的信道状态值Hi顺序由小到大排列。由式（8）可知，波束分配功率Pm的值也由小到大排列。假设第一个波束的分配功率为：

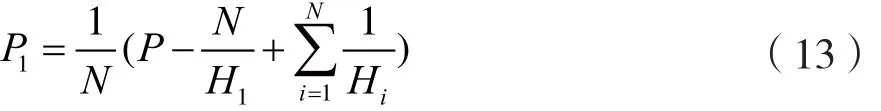
若计算出P1≤0，则令P1=0；给第二个波束分配功率的时候，将第一个波束状态值从中剔除。第二个波束的分配功率为：

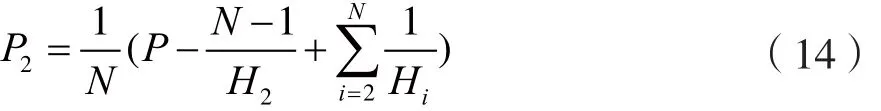
直到找到一个波束的分配功率满足Pm＞0，则后面的波束的分配功率按照式（10）求出。

在求出每个波束分配的功率后，根据约束条件Ci≤Ti,∀i，获得每个波束业务申请量和获得吞吐量之间的关系。如果Ci＞Ti，则令Ci=Ti，相应的波束的分配功率由确定。

整个算法的流程如图1所示。

这种改进的注水算法避免了迭代注水算法中每次求出各个波束上分配的功率后再修正更新β和ρ的值，很大程度上减少了运算量，避免了文献［5-6］中 线性功率分配算法中低SNR情况下功率分配值可能为负值的情况。

整个计算过程中，将所有波束的信道状态值Hi由小到大排序，运算量为O（Nlog2N）。根据式（13）、式（14）确定剔除的波束，然后再根据式（10）计算其余各波束上的功率，之后根据每个 波束业务申请量和获得容量之间的约束条件，确定每个波束的实际获得容量。其中，有（2+2N+M）次加法运算和（2+M）次乘法运算，M为被剔除的波束数目。对于波束获得容量的约束条件，最多有N次加法运算和2N次乘法运算，整个算法运算量为O（N）。可见，该改进算法的运算量与迭代注水算法一次迭代的运算量相当。

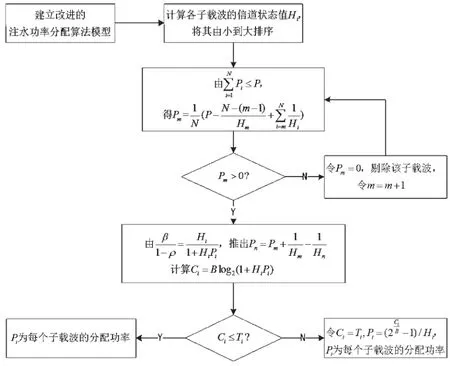
图1　改进注水算法流程

3　仿真分析

在仿真过程中，考虑多波束卫星通信系统FDMA体制下的下行链路传输。假设每个波束的带宽均为1 MHz，各波束信道衰减因子与噪声功率谱密度的比值αi/N0，i由1×105到5×105，可得到不同的波束信道条件Hi。在BER=10-5的条件下，考虑不同波束数目时的功率分配问题。由于算法将系统吞吐量作为功率资源分配问题的目标函数，因此以系统的吞吐量为标准对仿真结果进行对比。图2给出了用迭代注水算法和本文提出的改进注水算法，在系统不同波束数目条件下系统总容量的对比。

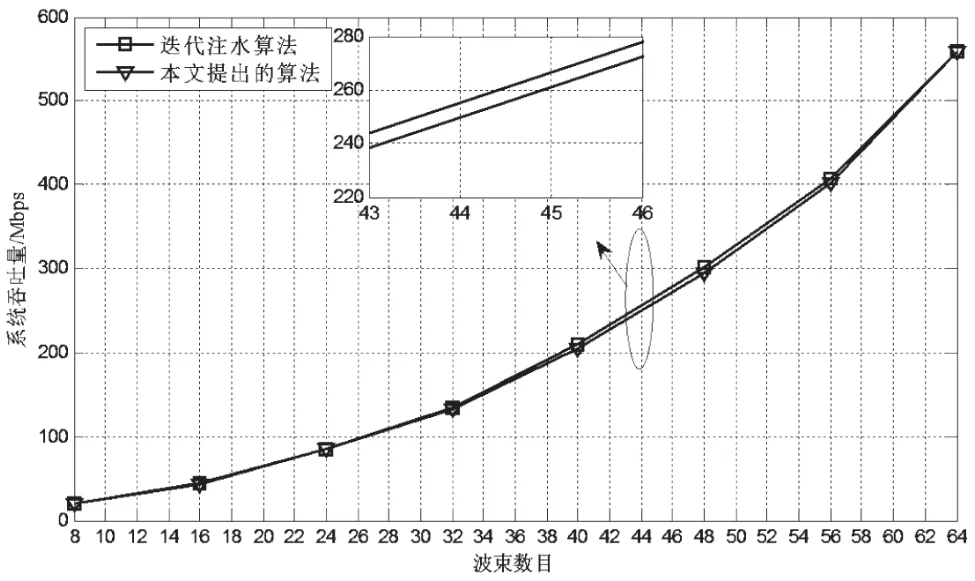
图2　不同波束数目条件下两种算法系统吞吐量对比

由图2可以看出，随着多波束卫星通信系统波束数目的增加，系统获得总容量增加；改进注水算法和迭代注水算法相比，在波束数目相同的情况下，系统总容量相差不大。

假设在原仿真条件基础上，设定波束数目N=32，在不同BER条件下对各波束进行功率分配。其中，C1和C2分别表示用迭代注水算法和改进算法进行功率分配后系统获得的总容量。仿真所得结果如表1所示。

表1　N=32时，不同BER下两种功率分配算法的系统吞吐量对比

表1列出了在N=32时，仿真所得在每种BER条件下两种功率分配算法的系统吞吐量。由表1可得，在波束数目一定时，随着多波束系统传输误码率BER的降低，改进注水算法的性能更加接近迭代注水算法的性能。这就意味着本文提出的改进注水算法在用户QoS要求较高时，算法优势明显。

图3给出了在不同BER、不同波束数目情况下两种功率分配算法下多波束卫星通信系统的吞吐量的对比图。

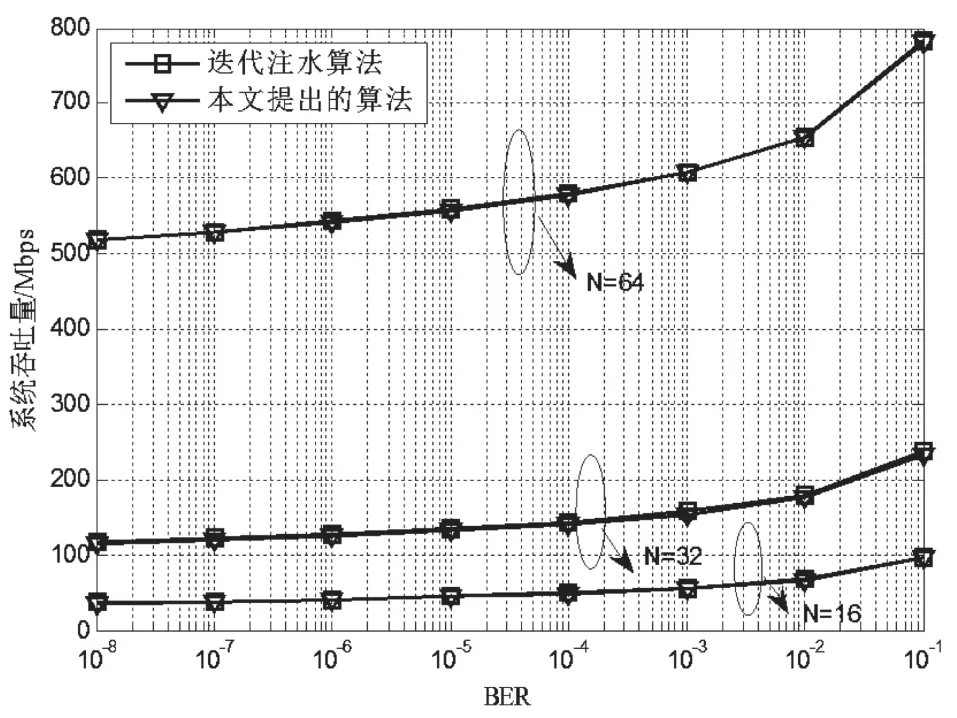
图3　不同BER条件下两种算法系统吞吐量对比

由图3可以清楚看出，波束数目为16、32和64时，迭代注水算法和改进注水算法的性能都很相近。在相同BER条件下，波束数目越多，系统吞吐量越大；而在相同波束条件下，BER越大，系统吞吐量越大；但是，改进注水算法和迭代注水算法在系统获得容量上相差不大。

现在已有条件下对计算的复杂度进行分析。假设在波束数目为N=32，BER=10-5的条件下对转发器功率进行分配。

图4和图5都是运用迭代注水算法进行功率分配所得到的仿真图。图4反映了算法的收敛性，在迭代次数为11时算法收敛。图5是算法的功率分配结果，可以看出前3个波束的功率分配均为0。由上述的算法复杂度分析，结合仿真结果，可以得到N=32时两种功率分配算法的运算量对比情况，如表2所示。

图4　N=32时迭代算法的收敛性

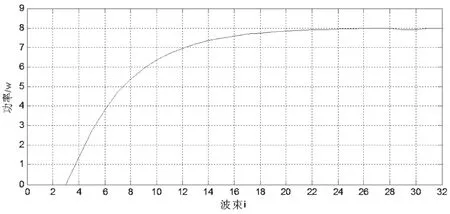
图5　N=32时每个波束的功率分配情况

表2　N=32时两种功率分配算法的运 算量对比

由表2中数据可得，本文提出的改进注水算法在运算复杂程度上大大小于迭代注水算法。

综上所述，本文提出的改进注水算法在系统吞吐量上与迭代注水算法相差不大，但是由于巧妙地避开了对偶变量的计算，有效降低了计算量，提高了算法性能。

4　结 语

本文对FDMA多波束系统的资源分配问题进行研究，针对传统迭代注水算法存在运算量大的问题，提出了一种改进的注水功率分配算法。通过推导分析和仿真，改进的注水算法可以在保证性能和迭代注水算法相差不大的情况下大大降低运算复杂度。此外，分析了系统传输误码率BER和波束数目对改进注水算法的影响，以期为相关研究提供助益。

［1］ Wang H，Liu A，Pan X，et al.Optimization of Power Allocation for a Multibeam Satellite Communication System with Interbeam Interference［J］.Journal of Applied Mathematics，2014，2014（01）：285-304.

［2］ Wang H，Liu A，Pan X，et al.Optimization of Power Allocation for Multiusers in Multi-Spot-Beam Satellite Communication Systems［J］.Mathematical Problems in Engineering，2014，2014（02）：1-10.

［3］ Feng Q，Li G，Feng S，et al.Optimum Power Allocation based on Traffic Demand for Multi-beam Satellite Communication Systems［C］.Communication Technology（ICCT），2011：873-876.

［4］ Destounis A，Panagopoulos A D.Dynamic Power Allocation for Broadband Multi-Beam Satellite Communication Networks［J］. IEEE Communications Letters，2011，15（04）：380-382.

［5］ Srivastava N K，Chaturvedi A K.Flexible and Dynamic Power Allocation in Broadband Multi-Beam Satellites［J］. IEEE Communications Letters，2013，17（9）：1722-1725.

［6］ Kan X，Xu X.Energy and Spectral-efficient Power Allocation in Multi-beam Satellites System with Co-channel Interference［C］. Wireless Communications & Signal Processing（WCSP），2015.

［7］ Wong I C，Shen Z，Evans B L，et al.A Low Complexity Algorithm for Proportional Resource Allocation in OFDMA Systems［C］.Signal Processing Systems，2004：1-6.

［8］ Shen Z，Andrews J G，Evans B L.Optimal Power Allocation in Multiuser OFDM Systems［C］.Global Telecommunications Conference，2004：337-341.

［9］ 张冬梅，徐友云，蔡跃明.OFDMA系统中线性注水功率分配算法［J］.电子与信息学报，2007，29（06）：1286-1289. ZHANG Dong-mei，XU You-yun，CAI Yue-ming. OFDMA System of Linear Water Injection Power Allocation Algorithm［J］.Journal of Electronics and Infor mation，2007，29（06）：1286-1289.

史 煜（1992—），女，硕士研究生，主要研究方向为卫星通信和资源分配技术；

张邦宁（1963—），男，硕士，教授，主要研究方向为卫星通信；

郭道省（1973—），男，博士，教授，主要研究方向为卫星通信；

杨 柳（1992—），男，硕士研究生，主要研究方向为卫星通信、功率分配技术。

A Modified Water-Filling Algorithm of Power Allocation for Multi-Beam Satellite Systems

SHI Yu， ZHANG Bang-ning， GUO Dao-xing， YANG Liu
（PLA University of Science and Technology， Nanjing Jiangsu 210007， China）

Allocating the power resource reasonably in satellite systems can improve the efficiency of resource. In order to solve the problem that the algorithm complexity based on using iterative water-filling algorithm to allocate power in multi-beam satellite systems is too high， a modified algorithm was proposed. The modified algorithm based on the limit of power and capacity takes the use of the same nonnegative dual variables of power allocation for each beam in Lagrange function to establish equation， so that we can get the whole results of power allocation as long as we know one of them. The iterative computations are voided with the modified algorithm while its complexity considerably decreases. Simulation shows that the modified algorithm is able to reduce the complexity of operation effectively， and its performance loss is very small compared with iterative water-filling algorithm at the same time. Meanwhile， the impacts of the BER and the number of beams on the modified algorithm are discussed.

multi-beam FDMA； power allocation； water-filling algorithm； complexity； bit error rate

TN927.2

A

1002-0802（2016）-10-1355-05

10.3969/j.issn.1002-0802.2016.10.017

2016-06-05；

2016-09-09

data：2016-06-05；Revised data：2016-09-09