一种基于多项式的非线性均衡器结构*

樊小琴，吉 磊，王 菊

（中国电子科技集团公司第三十研究所，四川 成都 610041）

一种基于多项式的非线性均衡器结构*

樊小琴，吉 磊，王 菊

（中国电子科技集团公司第三十研究所，四川 成都 610041）

提出一种基于多项式的接收端判决反馈非线性均衡器结构，并以QAM信号为例，进行理论分析与数值仿真。结果表明，当功放的饱和功率回退为3.5 dB时，所提非线性均衡器能显著改善功放带来的非线性失真，矫正接收星座点的幅度和相位畸变，使接收星座点更清晰，在误码率10-2处带来解调信噪比收益约4.4 dB。同时，发射端功放无需更多的功率回退来保证接收线性度，等效提升了发射功率。此外，所提非线性均衡器结构相对简单，且易于工程实现。

M-QAM调制；误码率；功放非线性；非线性均衡

0　引 言

随着社会的发展，人们对通信带宽的要求越来越高，而有限的频谱资源迫使厂商提升频谱效率。提升频谱效率的一种方案就是增加正交幅度调制（Quadrature Amplitude Modulation，QAM）的调制阶数。例如，第二代移动通信（2G）采用恒包络高斯最小键控（Gaussian Minimum Shift Keying，GMSK）［1］，而第四代移动通信（LTE-A）则采用了更高阶的64QAM调制［2］。

随着调制阶数上升，信号的峰均比（Peak to Average Power Ratio，PAPR）相应增加，对功放的线性度要求也更严格。常见的功放非线性补偿机制可分为两大类（如图1所示）：第一，发射信号预失真（Predistortion）［3-5］；第二，接收非线性均衡［6-11］。其中，非线性均衡不需要反馈通道，更容易实现。

图1　功放非线性补偿的两种方式

针对非线性均衡，文献［6］、文献［8］和文献［10］采用维纳模型、Volterra级数建模非线性，并采用递推最小二乘（RLS）更新Volterra级数的系数，实现非线性均衡。文献［7］采用Volterra级数建模非线性，并采用最小二乘法计算非线性系数。文献［9］采用神经Chebyshev多项式建模非线性，并采用梯度算法更新系数。文献［11］采用Volterra级数建模非线性，并采用基于最小误码率准则的滑窗随机梯度算法更新系数。

总结已有非线性均衡算法，主要区别在于非线性的建模方式和系数更新方法。在建模方式中，Volterra级数、神经Chebyshev多项式的实现复杂度高；系数更新方法中，最小二乘法需要矩阵求逆，RLS算法需要除法运算，不利于工程实现。

为考虑工程实现代价，本文提出一种基于多项式的判决反馈非线性均衡器结构，并通过仿真验证均衡器对功放非线性的补偿能力。

1　系统模型

接收信号可表示为：

式中，x是发射的理想信号；n为双边功率谱为N0/2的加性白高斯噪声；A（x）、φ（x）是发射放大器带来的幅度和相位畸变，其使接收信号y出现非线性分量；反映在频谱上，即3阶“鼓包”现象。

本文所提出的均衡器结构如图2所示。

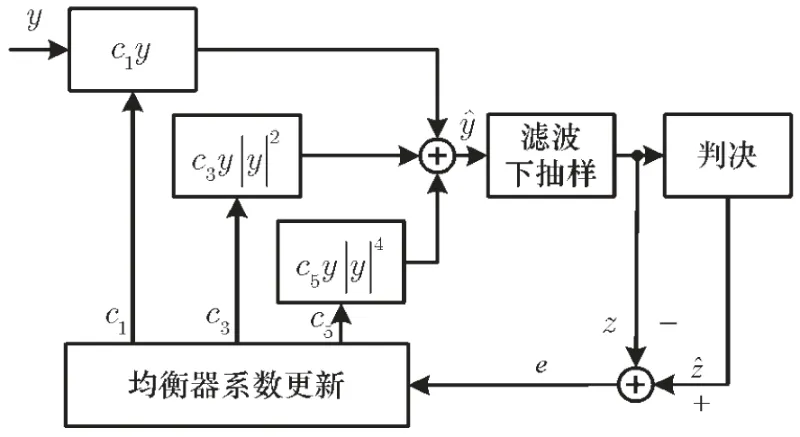
图2　基于多项式的非线性 均衡器模型

基于多项式的接收非线性均衡器可以表示为：

式中，c1、c3、c5是非线性均衡器的1阶、3阶和5阶系数，其中c3、c5用于补偿功放的非线性；y是非线性均衡器的输入信号，yˆ是非线性均衡器的输出信号。

非线性均衡器通过c1、c3、c5多项式拟合，补偿幅度失真A（x）和相位失真φ（x）的影响，以提升解调性能。

2　功放模型

本文的功放模型采用经典的行波管功率放大器（Travelling Wave Tube Amplifier，TWTA），幅度失真（AM-AM）和相位失真（AM-PM）模型分别为［12］：

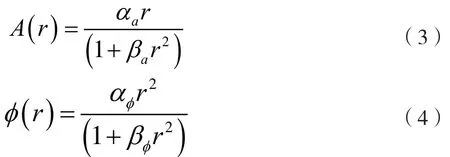
式中，αa、βaαφβφ由功放的物理特性决定。

输出功率回退（Output Back-Off，OBO）定义为：

式中，Pmax是功放的最大输出功率，Po表示功放的当前输出功率。

3　非线性均衡系数的计算

多项式系数c1、c3、c5有两种计算方案：静态计算和动态计算。

3.1 静态计算

假设输入长度N的矢量为Y=［y1，y2，…，yN］T，而期望输出矢量则非线性均衡过程可以表示为：

3.2 动态计算

为方便工程实现，系数更新过程可以用判决反馈获得误差，并采用最小均方误差（Least Mean Square，LMS）算法迭代更新非线性均衡器系数。

假设迭代步长为μ，LMS迭代过程可以表示为：

（2）1阶系数更新：

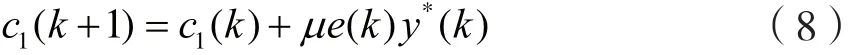
（3）3阶系数更新：

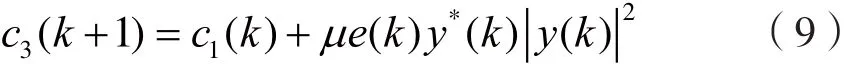
（4）5阶系数更新：

4　仿真结果及分析

仿真从星座点、功放特性曲线、功率谱、误码率和均方误差（MSE）多个维度分析非线性均衡器的收益。其中，仿真参数设置为：功放非线性模型参数αa=2.16，βa=1.15，αφ=4.0，βφ=9.1；调制方式64QAM，符号速率50 M/s，滤波器滚降因子0.25。

图3、图4依次为非线性均衡前、后的星座点。通过对比可看出，采用非线性均衡后的星座点更清晰，但外圈的星座点受非线性影响更大，矫正效果不如内圈点。

图5和图6展示了非线性均衡前后的AM-AM曲线和AM-PM曲线。可以看出，非线性均衡器确实能在一定程度上补偿功放的非线性。但AM-AM曲线中，高幅值的点较为散乱，补偿效果变差。对应到图4中，即外圈星座点变差。

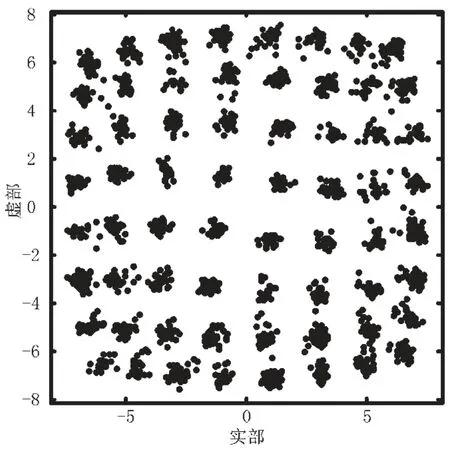
图3　非线性均衡前的星座点

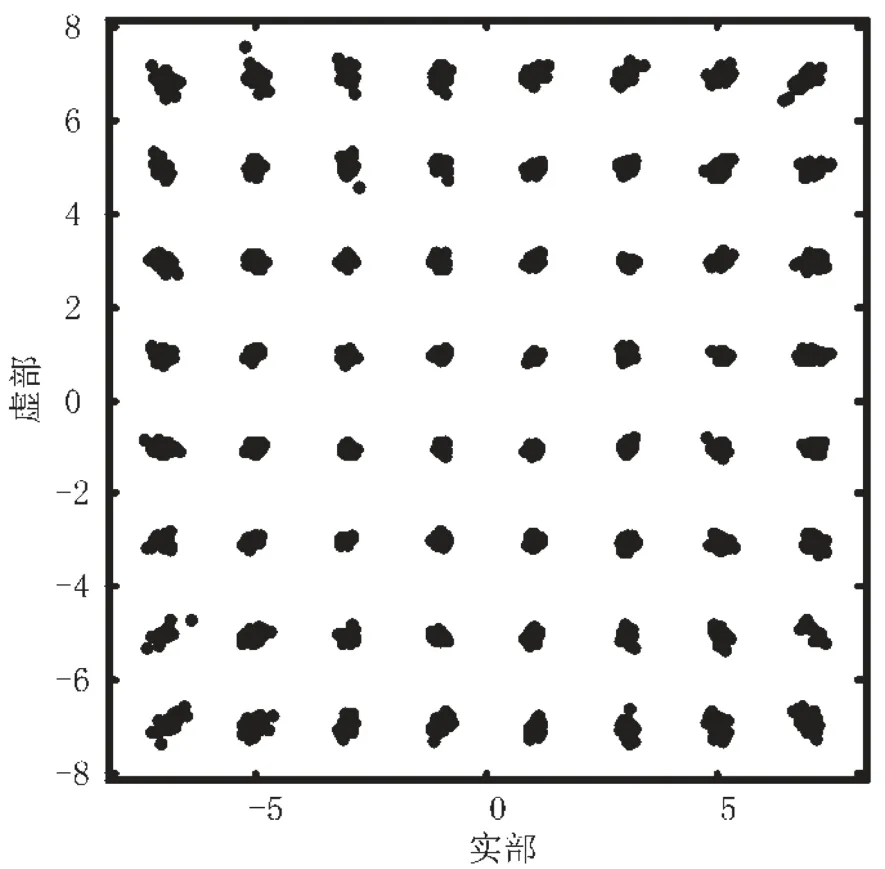
图4　非线性均衡后的星座点（OBO=3.5 dB）

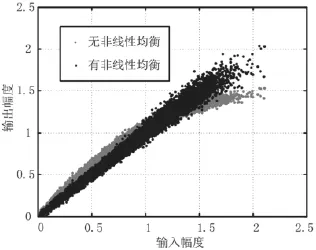
图5　非线性 均衡前后的AM-AM曲线（OBO= 3.5 dB）

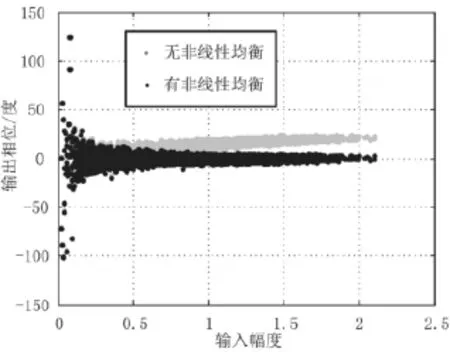
图6　非线性均衡前后的AM-PM曲线

图7给出了非线性均衡前后的功率谱对比。可以看出，通过非线性均衡，功放 3阶非线性失真分量被抑制，代价是接收底噪抬高了1.7 dB。究其原因，主要是非线性均衡器在消除非线性的同时放大了噪声。

图7　非线性均衡前后频谱（OBO=3.5 dB，SNR=35 dB）

图8给出了均衡前后的误码率。可以看出：没有非线性均衡时，误码率出现平层无法达到10-3，而采用非线性均衡后误码率没有平层现象。在误码率10-2点，非线性均衡带来的信噪比收益约4.4 dB。

图9给出了非线性均衡前后的MSE损失对比。可以看出：没有非线性均衡时，由于接收信号中非线性较强，故随着信噪比增加MSE损失越来越大；而采用非线性均衡后，MSE损失稳定在1.7 dB。

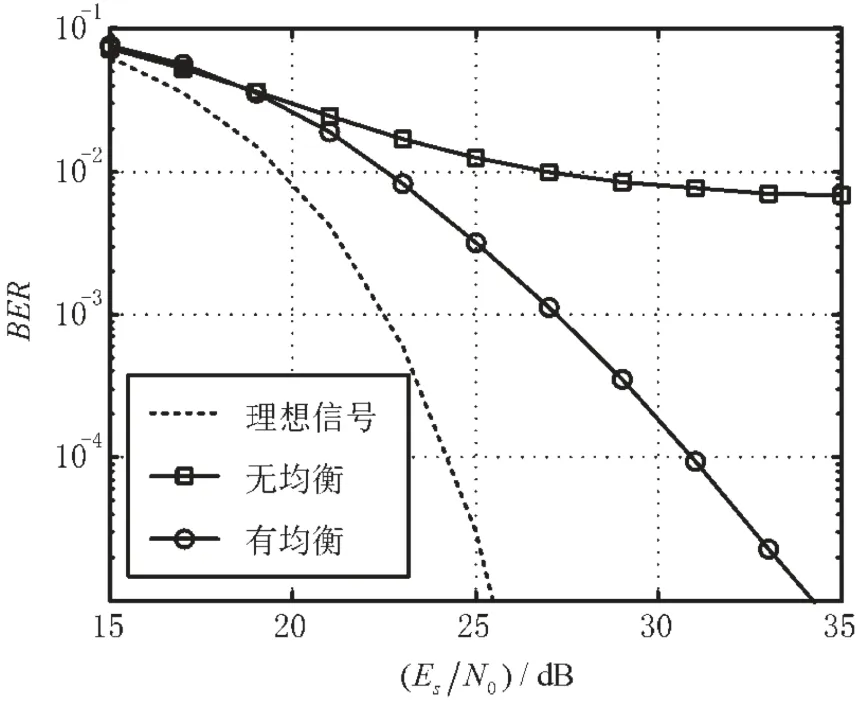
图8　非线性均衡前后误码率（OBO=3.5 dB）

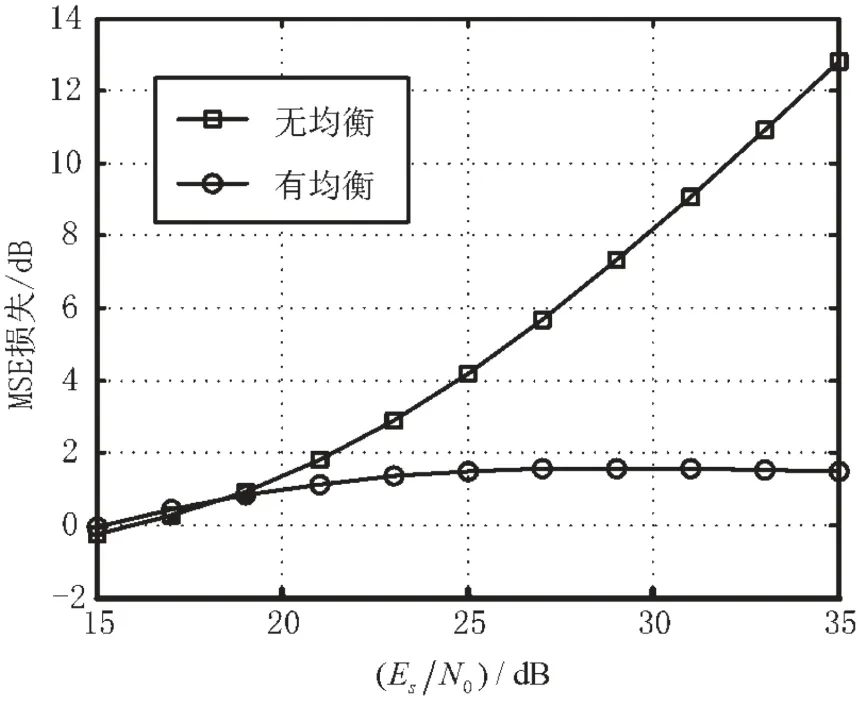
图9　非线性均衡前后MSE损失（OBO=3.5 dB）

5　结 语

本文提出了一种基于多项式的判决反馈非线性均衡 器结构，并仿真验证了该结构对接收性能的改善，等效提升了功放的发射功率。采用所述TWTA功放，OBO=3.5 dB时，解调信噪比收益可达4.4 dB；不同接收信噪比条件下，MSE损失小于2 dB。综上所述，所提非线性均衡器结构简单，易于工程实现。

［1］ 冯超，杨晨.一种基于GSM-R的GMSK信号调制解调方法的实现［J］.计算机与数字工程，2011，39（ 09）：157-160.

FENG Chao，YANG Chen.A Method of the Realization of the GMSK Modulation and Demodulation based on GSM-R［J］.Computer and digital engineeri ng，2011，39（09）：157-160.

［2］ 万彭，杜志敏.LTE和LTE-Advanced关键技术综述［J］.现代电信科技，2009，39（09）： 33-36. WAN Peng，DU Zhi-min.The Key Technologies of LTE and LTE-Advanced［J］.Modern Telecommunications Technology，2009，39（09）：33-36.

［3］ 王飞俊，金明录，孙鹏.一种数字预失真器的实现方法［J］.通信技术，2011，44（01）：154-156. WANG Fei-jun，JIN Ming-lu，SUN Peng.An Implementation of Digital Predistorter［J］.Communications Technology，2011，44（01）：154-156.

［4］ 邬书跃，田新广，黄丹等.微波功率放大器互调失真与数字基带预失真线性化技术［J］.通信技术，2001，34（0 3）：2-5. WU Shu-yue，TIAN Xin-guang，HUANG Dan，et al.IMD Distortion for Microwave Power Amplifiers and Digital Base-band Predistortion Linearization Technology［J］. Communications Technology，2001，34（03）：2-5.

［5］ 叶英勇，葛建华.一种自适应预失真器的实现及算法的改进［J］.通信技术，2002，35（12）：15-17. YE Ying-yong，GE Jian-hua.The Implementation of an Adaptive Predistorter and Modification of Its Algorithm［J］. Communications Technology，2002，35（12）：15-17.

［6］ 刘顺兰，蒋树南.非线性信道的均衡算法研究［J］.电子学报，2010，38（10）：2219-2223. LIU Shun-lan，JIANG Shu-nan.Equalization Algorithms based on Nonlinear Channel［J］. ACTA ELECTRONICA SINICA，2010，38（10）：2219-2223.

［7］ 张舰，彭启琮，邵甜鸽.基于最小二乘支持向量机的非线性均衡［J］.计算机工程与应用，2007，43（03）：92-95. ZHANG Jian，PENG Qi-cong，SHAO Tian-ge.Nonlinear Equalization based on Least Squares Support Vector Machine［J］.Computer Engineering and Applications，2007，43（13）：92-95.

［8］ 宋玙薇，杨守义，齐林.基于维纳模型的非线性信道接收端均衡方案［J］.电视技术，2012，36（05）：8 3-85. SONG Yu-wei，YANG Shou-yi，QI Lin.Receiving-end Equalization Scheme for Nonlinear Channel based on Wiener Model［J］.Video Engineering，2012，36（05）：83-85.

［9］ 邓晓红，张家树.神经Chebyshev正交多项式均衡器及自适应算法［J］.西南交通大学学报，2005，4 0（02）：163-167. DENG Xiao-hong，ZHANG Jia-shu.Neural Chebyshev Orthogonal Polynomial Equalizer and Its Adaptive Algo-rithm［J］.Journal of Southwest Jiaotong University，2005，40（02）：163-167.

［10］ 李良山，杨育红，王兰.卫星通信中快速非线性信道RLS均衡算法［J］.信号处理，2016，32（04）：4 51-456. LI Liang-shan，YANG Yu-hong，WANG Lan.A Fast Nonlinear Channel RLS Equalization Algorithm in Satellite Communication［J］.Journal of Signal Processing，2016，32（04）：451-456.

［11］ 朱仁祥，吴乐南.最低误码率非线性均衡器的快速自适应学习算法［J］.电路与系统学报，2012，17（02）：88-94. ZHU Ren-xiang，WU Le-nan.Adaptive Learning Algorithms with Fast Convergence Rate for Minimum Bit Error Rate Nonlinear Equalizers［J］.Journal of Circuits and Systems，2012，17（02）：88-94.

［12］ ELENA COSTA，SILVANO PUPOLIN.M-QAM-OFDM System Perfor mance in the Presence of a Nonlinear Amplifier and Phase Noise［J］.IEEE Transactions On Co mmunications，2002，50（03）：462-472.

樊小琴（1982—），女，硕士，高级工程师，主要研究方向为通信与信号处理；

吉 磊（1984—），男，硕士，工程师，主要研究方向为抗干扰通信；

王 菊（1986—），女，硕士，工程师，主要研究方向为信道估计算法及FPGA实现。

Polynomial-based nonlinear equalizer

FAN Xiao-qin， JI Lei， WANG Ju
（No.30 Institute of CETC， Chengdu Sichuan 610041， China）

A polynomial-based nonlinear decision feedback equalizer structure is proposed， and with QAM signal as an example， the theoretical analysis and numerical simulation are done. The simulation results indicate that when the amplifier output back off is 3.5dB， the proposed nonlinear decision feedback equalizer could noteworthily improve the nonlinear distortion resulted from power amplification， and bring a signal-to-noise ratio gain of 4.4dB at a bit error ratio of 10-2. In addition， the amplifier do not require more output power back off to keep the signal linearity， and this is equal to raising the transmit power. All this indicates that the proposed nonlinear equalizer is relatively simple in structure and easy for engineering implementation.

M-QAM； BER； power-amplifier nonlinearity； nonlinear equalizer

TN911.22

A

1002-0802（2016）-10-1326-05

10.3969/j.issn.1002-0802.2016.10.012

2016-06-13；

2016-09-21

data：2016-06-13；Revised data：2016-09-21