卫星通信系统OFDM同步算法研究*

段红光，王利飞，黎奇京，卢松品

（重庆邮电大学 通信与信息工程学院，重庆 400065）

卫星通信系统OFDM同步算法研究*

段红光，王利飞，黎奇京，卢松品

（重庆邮电大学 通信与信息工程学院，重庆 400065）

针对卫星移动通信的同步问题，提出了一种新的基于OFDM传输方式的卫星通信系统的时间和频率同步算法。大多数的时间和频率估计算法都是通过训练序列前后相同部分的相关性进行时偏和频偏的计算，而很少有文献考虑到利用恒包络零自相关序列（CAZAC）的强相关性来进行OFDM符号的同步。因此，提出的改进算法充分考虑了频偏对定时估计的影响，从而直接利用训练序列的强相关性进行OFDM同步，包括符号定时估计、整数频偏估计和小数频偏估计。仿真结果表明，改进算法的性能对比常用的算法有了显著提高，并且计算复杂度也不高。

卫星通信；OFDM；训练序列；定时估计；频偏估计

0　引 言

卫星通信作为地面移动通信的一种补充，在国家的民生、经济、国防军事方面占有举足轻重的作用。近年来，为满足数据的高速传输需要，卫星通信系统也朝着宽带高传输速率方向发展，因此研究基于OFDM的卫星通信系统同步技术具有实际意义。然而，OFDM系统对定时偏差和频率偏差非常敏感，因此有很多文献对OFDM系统的同步算法进行了论述。文献［1］提出了一种由两个OFDM符号组成的训练序列，第一个训练序列用于符号定时估计和小数倍频偏估计，第二个训练序列用于整数倍频偏估计。然而，该方法由于循环前缀的影响，会导致定时估计曲线出现一个“高原区”。严格地说，它基本达不到符号定时的估算，只能起到信号检测作用。文献［2-3］是对文献［1］符号定时估计的改进，它们设计出了相关特性更为良好的训练序列，从而提升了符号定时估算性能。文献［4］从频域角度入手进行频偏估计，相比文献［1］提高了小数倍频偏的估计精度，但牺牲了估计范围。后续还有许多文献提出了各种各样的方法，但基本均是基于文献［1］进行的该井，在此不再详述。然而，这类为大家熟知的方法几乎都是利用训练序列内部部分序列的相关性，却并没有充分考虑利用训练序列已知的这个条件。

本文提出一种利用CAZAC序列进行同步的方法，采用Zadoff-Chu序列（以下简称chu序列）来构造训练序列。chu序列具有相关峰尖锐，旁瓣为零，FFT变化后还是一个chu序列的良好特性。但是，chu的相关特性会受到整数倍频偏的影响。本文将利用这一特性，重新设计帧头结构，利用此帧结构和重新定义的估算函数，无需进行FFT运算，直接在时域内进行符号定时估计和整数频偏估计，从而降低同步算法的运算复杂度，在低信噪比信道下性能优于文献［1-2］。

文章的结构组织如下：第二部份描述一般的OFDM系统模型；第三部份阐述改进的同步算法；第四部分给出仿真结果和性能比较；第五部分得出结论。

1　系统模型和频偏对chu序列的影响

1.1 系统模型

图1给出了OFDM系统的模型图。

图1　系统模型

假设有N个子载波，OFDM符号可以表示为：

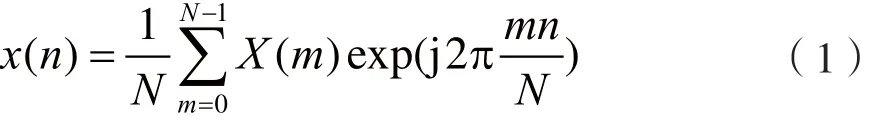
式中，0≤n≤N-1，X（m）是第m个子载波上的已调数据，N是总的子载波数目。为了克服符号间干扰（ISI），在OFDM符号前添加循环前缀（CP），经过多径信道后，信号y（n）可以表示为：

式中，L为多径的数目，hl为第l个离散多径信道的时域冲激响应。考虑到加入时移、频移以及噪声的影响，接收信号r（n）为：

式中，δ是时间偏移，ε是以子载波间隔为标准的归一化频偏，w（n）是均值为0、方差为σ2w的高斯白噪声。在接收端需要补偿频率和时间偏差，以便正确恢复发送数据。如图1所示，本文的目地就是估计出时间偏差和频率偏差，从而完成图1中的定时和频率同步。

1.2 频偏对chu序列的影响

长度为N（cNc为偶数）的chu序列，可以表示为：

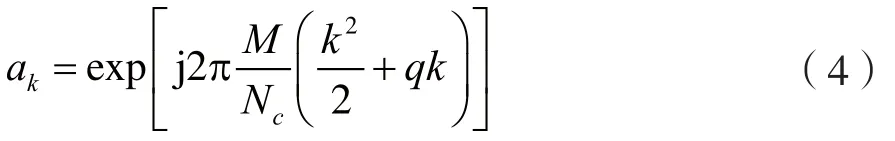
式中，0≤k≤Nc-1，Nc是序列长度，M与Nc互质，q是任意整数。不失一般性地，取M=Nc-1，故chu序列的自相关性可表示为：

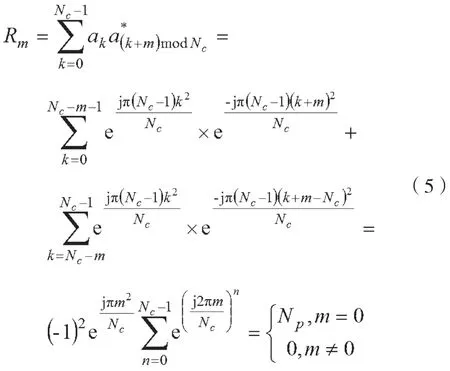
考虑到信号经过信道传输后存在频偏，所以本地已知的训练序列和接收到存在频偏的序列的互相关性为：

其中，c=N/Nc是移位因子。

由式（6）可以看出，频率偏差会使chu序列相关函数的峰值产生移动，但是并不会影响相关峰值的幅度。图2是利用matlab仿真软件对该特性进行的验证，结果符合由式（6）推导出的结论。

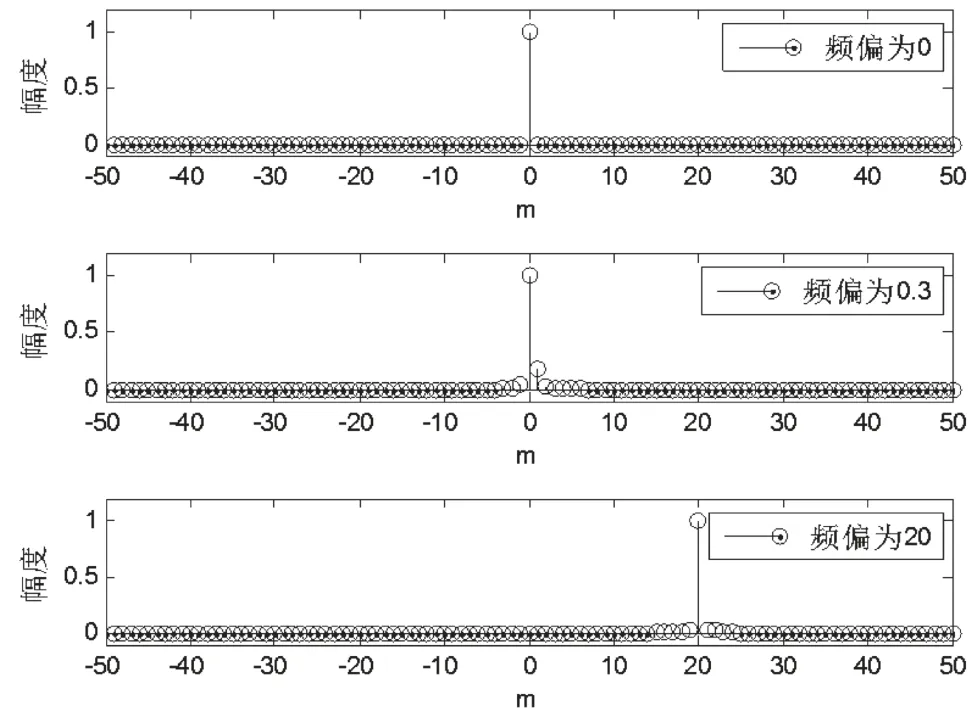
图2　频偏对chu序列的影响

2　改进算法阐述

2.1 帧结构设计

根据1.2小节的描述，重新设计帧结构，如图3所示。训练序列长度为一个OFDM符号，由三部分组成，前两部分是长度为N/4的、完全相同的chu序列S1，后一部分是长度为N/2的chu序列S2。

图3　帧结构

2.2 同步算法描述

在接收端分别用序列S1、S2和接收信号进行相关运算。由于chu序列良好的相关性质，故肯定会出现类似冲激状峰值的曲线，峰值的位置由正确的符号定时点和εi/c两项共同决定。定义S1和S2的时间估计函数：

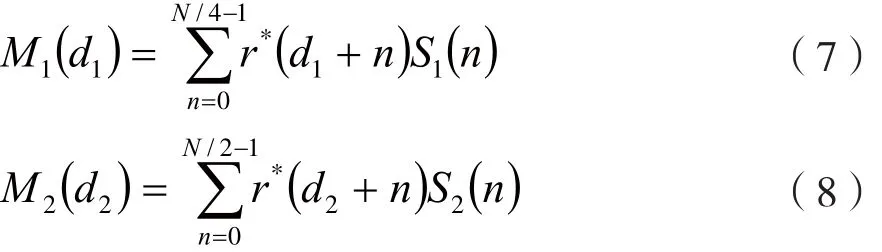
式中，S1（n）和S2（n）分别是序列S1和S2。

很明显，M1（d1）和M2（d2）都具有冲激状的曲线，其最大值处的d值估计为：

由于c1=4、c2=2，所以d1est和d2est有如图4所示的关系。

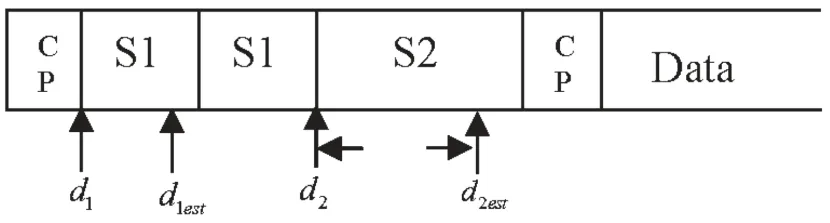
图4　偏差示意

由图4很容易得出整数倍频偏εi的估计值：

由式（11）的结果可以得到符号定时估计值：

得出符号定时位置和整数倍频偏后，小数倍频偏可以利用训练序列1，采用与文献［1］类似的估计方法得出，此处不再叙述。图5为改进算法同步原理图。

图5　同步原理

3　仿真结果和性能比较

表1列出了相关仿真的参数取值。

表1　仿真参数

图6给出了文献［1-2］和改进算法的定时度量曲线。由图6的反震结果可知，改进算法在正确定时处出现峰值，而在其他点定时函数度量值接近于0。可见，相比于文献［1-2］给出的算法，改进算法的定时结果更精确。

图6　定时度量曲线

图7给出了在不同性噪比环境下的符号定时的正确捕获概率。由于Schmidl算法正确捕获的概率几乎为0，故在此仅画出文献［2］和改进算法的正确捕获概率曲线图。从图中可以看到，改进算法在-5dB左右时就可达到100%的正确捕获概率，而文献［2］则须在12 dB左右才能达到。

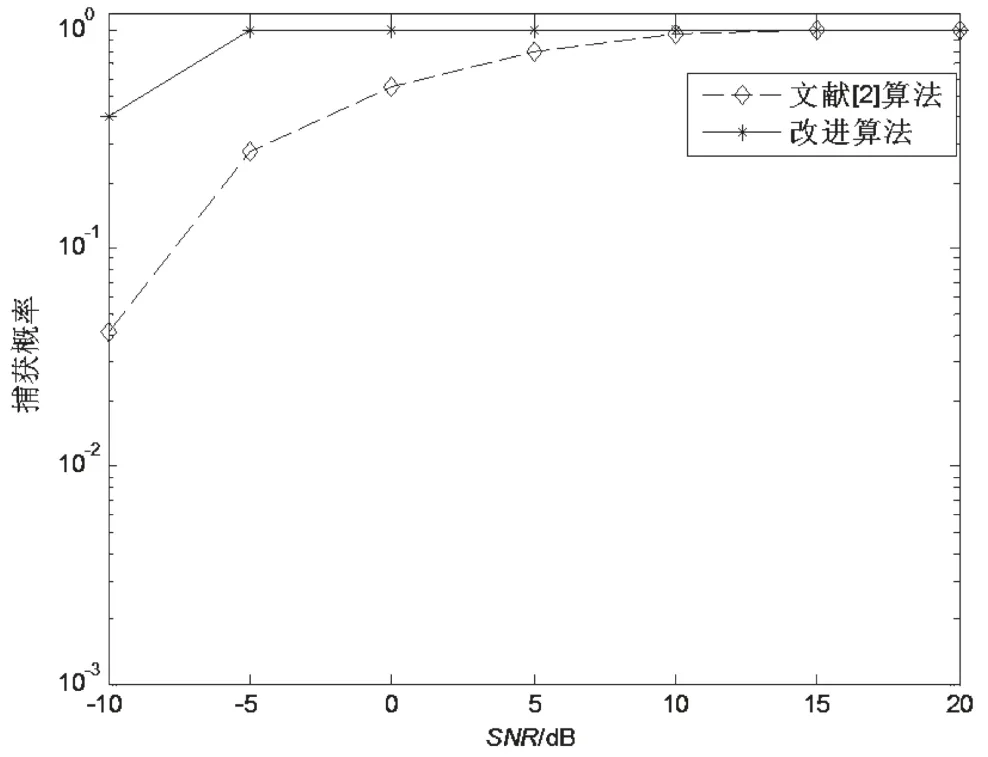
图7　捕获概率

图8给出了文献［1］、基于循环前缀的算法和改进算法的频率偏差估计的均方差。相比之下，改进算法的性能有所提高。在-5dB后，改进算法的性能提高明显。

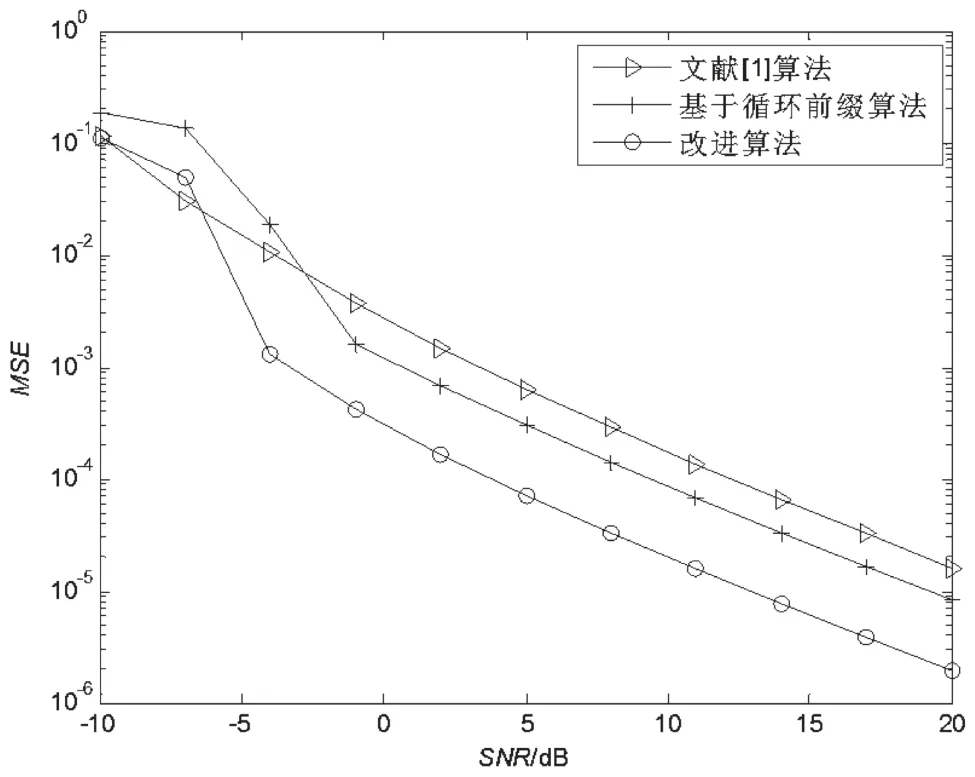
图8　频偏估计方差

4　结 语

本文提出的改进算法利用CAZAC序列的良好自相关和互相关特点，充分利用频偏对序列相关性的影响，得出了同步估计方法。经过讨论分析可知，相对文献［1-2］，改进算法在信噪比-5dB之后性能都有了极大提升，且改进的同步算法可以工作于低信噪比条件下。

［1］ Schmidl T M，Cox D C.Robust Frequency and Timing Synchronization for OFDM［J］.IEEE Transactions on Com munications，1997，45（12）：1613-1621.

［2］ Minn H，Zeng M，Bhargava V K.On Timing Offset Estimation for OFDM Systems［J］.IEEE Communications Letters，2000，4（07）：242-244.

［3］ Park B，Cheon H，Kang C.A Novel Timing Estimation Method for OFDM Systems［J］.IEEE Communications Letters，2003，7（05）：239-241.

［4］ Moose P H.A Technique for Orthogonal Frequency Division Multiplexing Frequency Offset Dorrection［J］.IEEE Transactions on Communications，1994，42（10）：2908-2914.

［5］ 贾鹏，唐远，黄尧.SOQPSK信号位定时与载波联合估计算法［J］.通信技术，2015，48（12）：1339-1342.

JIA Peng，TANG Yuan，HUANG Yao.Joint Estimation Algorithm of SOQPSK Signal Bit Timing and Carrier［J］.Communications Technology，2015，48（12）：1339-1342.

［6］ Thierry Pollet，Mark Van Bladel，Mare Moeneclaey. Bersensitivity of OFDM Systems to Carrier Frequency Offset and Wiener Phase noise［J］.IEEE Transaction on Communications，1995，34（06）：191-193.

［7］ 郑娟.宽带无线OFDM系统同步算法的研究［M］.北京：北京邮电大学，2008. ZHENG Juan.Research on Synchronization Algorithm for Broadband Wireless OFDM System［D］.Bei jing：Beijing University of Posts and Telecommunications，2008.

段红光（1969—），男，硕士，正高级工程师，主要研究方向为新一代宽带移动通信核心芯片、协议及系统应用；

王利飞（1990—），男，硕士研究生，主要研究方向为卫星移动通信系统；

黎奇京（1990—），男，硕士研究生，主要研究方向为卫星移动通信系统；

卢松品（1990—），男，硕士研究生，主要研究方向为卫星移动通信系统。

OFDM Synchronization Algorithm for Satellite Communication System

DUAN Hong-guang， WANG Li-fei， LI Qi-jing， LU Song-pin
（School of Communication and Information Engineering Chongqing University of Posts and Telecommunications， Chongqing 400065，China）

Aiming at the synchronization of satellite mobile communication， a new time-and-frequency synchronization algorithm based on OFDM transmission mode for satellite communication system is proposed. Most of the time-and-frequency estimation algorithms， usually through the same part of the correlation in before and after the training sequence， implements time offset and frequency offset calculation， while few literatures consider the use of CAZAC （Constant Amplitude Zero Auto Correlation） strong correlation in OFDM symbol synchronization. For this reason， an improved algorithm fully considering the impact of frequency offset on timing estimation is proposed， thus directly using the strong correlation of training sequence for OFDM synchronization， including for symbol timing estimation， integer carrier frequencyoffset estimation and fractional frequency-offset estimation. Simulation results indicate that the improved algorithm， with fairly low computational complexity， is clearly better in performance as compared with the traditional algorithms.

satellite communication； OFDM； training sequence； timing estimation； frequency-offset estimation

TN927.23

A

1002-0802（2016）-10-1312-05

10.3969/j.issn.1002-0802.2016.10.009

2016-06-16；

2016-09-22

data：2016-06-16；Revised data：2016-09-22