PID+控制算法的研究
王喜明
(中国电子科技集团公司第五十四研究所,河北 石家庄 050081)
PID+控制算法的研究
王喜明
(中国电子科技集团公司第五十四研究所,河北 石家庄 050081)
辨识一个控制系统的模型比较复杂,PID控制不需要掌握系统的精确模型,就可以使系统稳定的工作,因此PID控制得到广泛应用。通过对常规PID控制算法的介绍,引出了PID+控制算法。针对数字控制系统应用需求,以及数字系统在很多领域已经替代模拟系统的情况下,给出了PID+数字化的方法,最后介绍了数字PID+参数整定的过程。PID+控制是PID控制的改进,PID+控制器能够完成任何一种PID控制器所能完成的任务。
控制器;参数;滤波;PID+
PID控制是最早发展起来的一种控制策略,具有算法简单、鲁棒性好和可靠性高的优点,被广泛应用于过程控制和运动控制中。PID控制器可以通过设置三个增益中的一个或者两个为零来简化。PID+是PID控制的一种改进,它能完成任何一种简单控制器所能完成的任务。PID+控制不需要详细的被控对象的模型,通过PID+参数整定,就可以很方便的调试好控制系统。数字PID+控制比模拟PID+控制复杂,但是现代微处理器的处理速度非常的快,数字PID+可以完全取代模拟PID+控制,程序实现也比较简单。
1 PID控制器原理介绍
伺服控制系统是典型的反馈控制系统,笔者以伺服系统为例来介绍PID控制。伺服控制系统通常有位置控制器、速度控制器、电流控制器。每一个控制器都是比例、积分和微分增益的组合[1]。常规PID控制器结构框图如图1所示。

图1 PID控制器结构框图
PID控制表达式为如式1所示。

式中PK为比例增益,DK为微分增益,IK为积分增益。
比例增益设置了控制器性能的边界,其控制律简单,控制量是偏差的比例,运行简单,易于调试。然而,P控制律的主要缺点是存在稳态误差,稳态误差在某些场合是不能容忍的。积分增益提供了稳态抗偏差能力,积分增益越大,稳态抗偏差能力就越强。然而积分有90°的相位滞后,这会减小相位裕度,常见的结果就是超调和震荡。控制器中增加积分,使得饱和问题变得复杂,为避免饱和,在积分过程中必须采用防止饱和的措施。微分增益借助于微分90°的超前相位超前了控制回路的相位,使用微分增益通常能提升系统的响应能力,但是微分增益对噪声很敏感,容易引起振荡。
2 PID+控制原理介绍
PID+控制是PID控制的改进。PID+控制对指令信号进行滤波,允许有更高的积分增益,可以改善系统稳态抗偏差能力,同时消除超调。但是PID+控制指令响应的速度随抗偏差能力的改善而下降。PID+控制框图如图2所示。
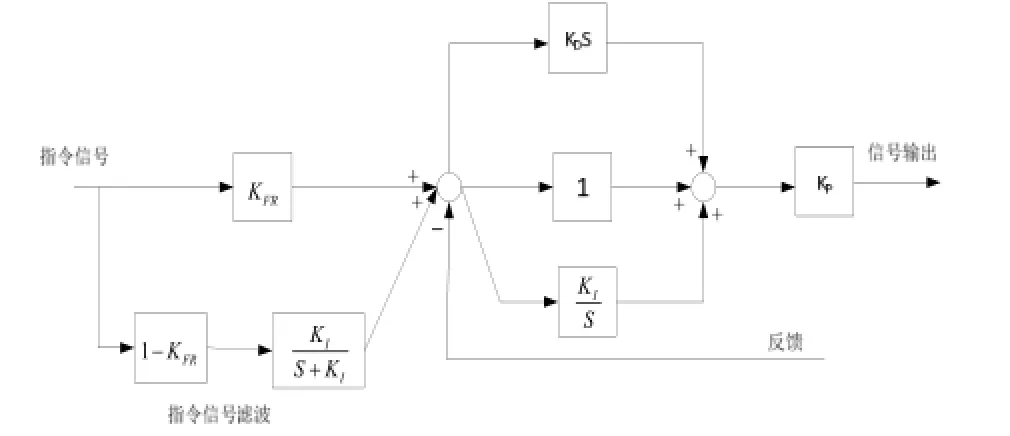
图2 PID+控制框图
PID+控制对指令滤波的程度决定于增益KFR,当KFR为1时,所有的滤波作用消除,控制器等同于常规PID控制器,当大于零小于1时,滤波起作用,但是指令的响应能力降低。的最优值依赖于具体的应用场合,根据实际情况选用KFR的值。把KI作为指令滤波器的转折频率,在消减由积分增益所产生的超调方面是最优的,同时控制算法也容易实现[1]。
由图2可以推导出PID+控制率的表达式,
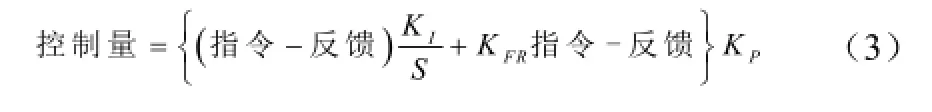
式(3)与PI+控制表达式是等价的,式(3)是PI+非常有用的备选方法,由于在积分前没有乘法,因此很容易避免噪声,程序实现方法也很简单。
3 数字PID+控制原理介绍
性能优良的微处理器已经用于控制领域,具备廉价的数字控制器已经在许多领域取代了模拟控制器。数字PID+控制应用广泛,参数调试比模拟PID+调试方便。 由于PID+控制含有积分和和微分,首先要把积分和微分数字化。数字积分与数字微分的方法很多,工程上常用的、易于实现的是欧拉积分和简单差分。欧拉积分和简单差分都可以设置

式中T为采样周期。
如果应用PI+控制策略,把式(4)代入式(3),得
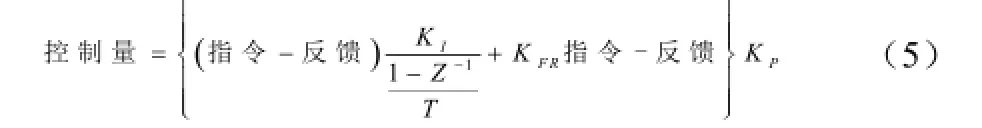
如果应用PID+控制策略,把式(4)代入式(3),得
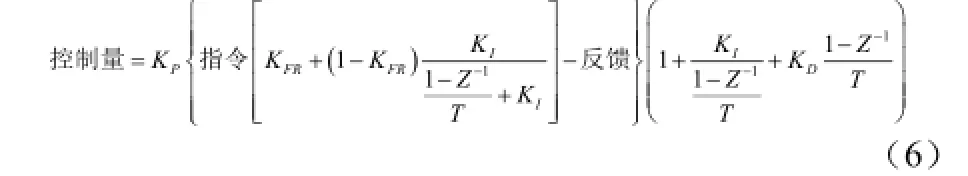
把式(6)分为式(7)和式(8)两个部分,前一部分的输出作为后一部分的输入,分别数字化,实现起来也比较方便。

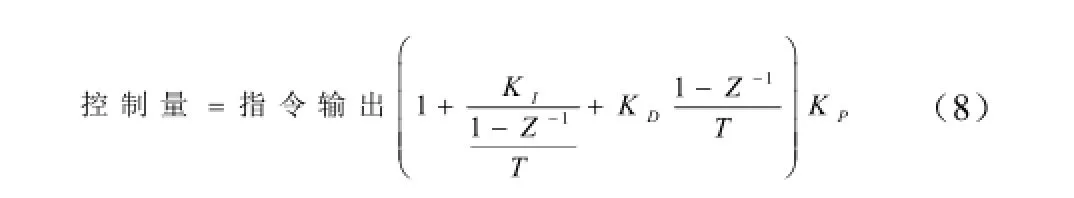
4 数字PID+的程序实现方法
为了计算机程序实现的方便,先要推导出表达式的差分方程形式。对于式(5),控制量为U,输入R,输出反馈为C。可以得出
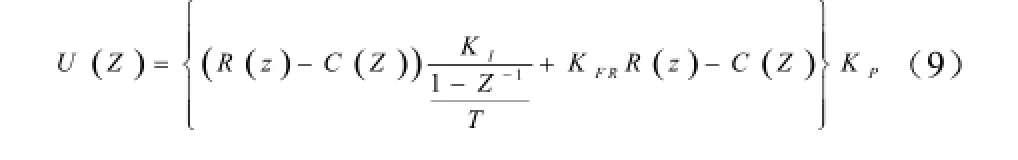
整理后得到式(10)
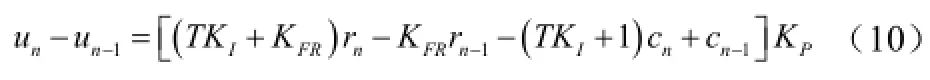
式(10)为PI+的差分方程形式,很容易用程序递推实现。
PID+数字实现相对复杂一些,分两段分别进行离散化,指令滤波与反馈之差作为第一级,第二级为常规PID,第一级的输出为第二级的输入,他们之间是串联关系。
对于式(7),设指令为R,反馈为C,指令输出为E,经推导,得出如下表达式
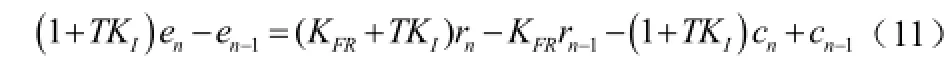
输出e作为常规PID的输入,推导得到
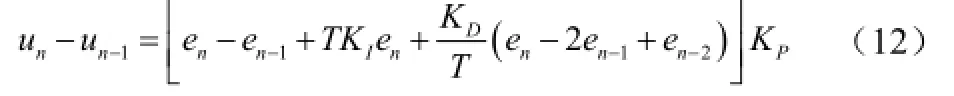
式(12)是常规增量PID的差分方程表达式。在程序实现的时候,可以把式(11)写成一个函数,式(12)写一个函数。第一个函数的返回值,作为下一个函数的输入,程序实现比较简单。
5 PID+的参数整定
PID+控制的调试与常规PID控制调试方法类似。采用周期T为常量,根据不同的控制对象,T取不同的值。有四个参数需要整定,分别为PK、IK、DK、FRK。PID+参数的调试过程[2]如图3所示。

图3 PID+控制调试过程
图3所示的FRK的值为经验值,工程应用中可以在经验值的基础上微调,以达到最佳效果。
6 结论
本文讲述的PID+的控制方法,在某精密跟踪雷达伺服控制系统中成功运用,输入方波信号,调试陀螺环和跟踪环,输出几乎没有超调。PID+控制方法能适应任何控制领域,本方法具有一定的实用价值。
[1] 孙宇,王志文,孔凡丽,等.交流伺服系统设计指南[M].北京:机械工业出版社,2013.
[2] George Ellis.控制系统设计指南[M]. (第3版)刘君华,汤晓君,译.北京:电子工业出版社,2006.
Research of PID+ control algorithm
The model of control system is difficult to recognize, and the system is worked perfectly by control of PID when model is not acquired exactly, so control of PID is widely used. Through the introduction of normal PID control algorithm, PID+ is proposed,and the theory of PID+ is presented. In order to deal with need of digital control system, and analog system is instead of digital system,the method of digital process is presented, and then the adjusting of parameter of PID+ is introduced. PID+ control theory is improved from PID. if the task could be completed by PID controller, also it is completed by PID+ controller.
Controller; parameter; filtering; PID+
TN821
A
1008-1151(2016)04-0004-02
2016-03-13
王喜明(1978-),男,陕西西安人,中国电子科技集团公司第五十四研究所工程师,从事天线伺服控制系统设计。

