桁架式钢骨混凝土梁抗弯极限承载力计算分析

赵文霞，　邓志恒

(1.大连科技学院 实验中心， 辽宁 大连 116052；2.广西大学 土木建筑工程学院， 广西 南宁 530004)



桁架式钢骨混凝土梁抗弯极限承载力计算分析

赵文霞1，邓志恒2

(1.大连科技学院 实验中心， 辽宁 大连 116052；2.广西大学 土木建筑工程学院， 广西 南宁 530004)

利用有限元分析软件ABAQUS对桁架式钢骨混凝土梁进行受力分析，并将模拟结果与试验数据对比，二者吻合度良好，表明本文有限元分析的可行性。通过改变斜腹杆面积探讨斜腹杆对其抗弯极限承载力的影响，分析结构表明：随着斜腹杆面积的增加，构件抗弯极限承载力逐渐增大。根据模拟结果推导出考虑斜腹杆作用的桁架式钢骨混凝土梁抗弯极限承载力的计算公式。将修正后的计算结果与试验结果进行对比，表明计算精度进一步提高。

桁架式钢骨混凝土梁；有限元分析；斜腹杆；抗弯极限承载力计算

钢骨混凝土结构主要分为实腹式钢骨混凝土结构和空腹格构式钢骨混凝土结构。桁架式钢骨混凝土梁是空腹格构式钢骨混凝土结构的一种，与传统的角钢布置在四角，栓钉连接钢板角钢不同，它创新地运用T型钢代替角钢作为钢桁架的上下弦杆，用角钢连接T型钢作为腹杆，最后将钢桁架整体焊接嵌入到混凝土中[1]。与实腹式钢骨混凝土梁相比，这种新型结构梁可以根据实际工程的需要改变型钢骨架的大小和位置，由于型钢骨架布置的灵活性，为施工提供了方便[2]。与传统的空腹格构式钢骨混凝土梁相比，钢桁架中的腹杆增强了型钢骨架和混凝土之间的粘结作用，对梁内混凝土起到了很好的约束作用。不仅可以不设置栓钉，而且提高了构件的承载力[3]。目前国内外关于桁架式钢骨混凝土梁的研究还不够成熟，对于其抗弯极限承载力的计算没有明确的计算方法和统一的计算公式，通常是将上下弦杆看作纵筋，然后采用钢筋混凝土结构设计原理进行计算，由于没有考虑腹杆的作用，计算结果与试验结果相差过大。

本文通过有限元分析软件ABAQUS对桁架式钢骨混凝土梁受力过程进行模拟，并将模拟结果与课题组的试验数据进行对比，以验证模拟的合理性。然后通过斜腹杆与下弦杆面积比值的改变，探讨斜腹杆面积对桁架式钢骨混凝土梁抗弯极限承载力的影响。根据模拟结果引入斜腹杆面积增大系数，提出考虑斜腹杆作用的桁架式钢骨混凝土梁抗弯极限承载力计算公式。最后将计算结果与试验结果进行对比，吻合度良好，与不考虑斜腹杆作用的抗弯极限承载力计算结果相比精度有所提高。为今后的桁架式钢骨混凝土梁抗弯极限承载力的研究提供依据[4]。

1　桁架式钢骨混凝土梁受力分析

1.1有限元模型的建立

1.1.1混凝土和钢材的本构关系

混凝土采用混凝土损伤塑性模型。本文混凝土损伤模型采用《混凝土结构设计规范(GB50010—2010)》[5]附录C.2的混凝土本构关系，通过输入单轴压缩应力-应变曲线、受压损伤因子、单轴拉伸应力-应变曲线、受拉损伤因子，建立混凝土材料的本构模型。本构件主要起承重作用的是T型钢和角钢，因此T型钢和角钢采用弹塑性强化模型。为了便于计算纵筋和箍筋本构关系可以简化为理想弹塑性模型[6]。

1.1.2单元类型的选取

(1)型钢。型钢采用C3D8I，能够克服线性完全积分单元中的剪切自锁问题。本文分析的问题属于纯弯曲问题，只需较少的积分点就可以得到比较高的计算结果，而且与二次单元相比计算成本明显降低，对于非线性问题非协调单元有着明显的优势。但如果所关心的部位扭曲变形比较大，分析精度就会下降。型钢是本次模拟主要承重的构件，计算精度要求比较高。因此型钢选择八节点六面体线性非协调模式单元C3D8I[7]。

(2)混凝土。混凝土采用C3D8R单元。线性减缩单元的成本较低，但是它们却以最低的成本给出了最好的结果，在弯曲荷载下不容易发生剪切自锁。当网格划分较粗时，分析精度不会明显下降。C3D8R是一个八节点六面体线性减缩单元，与普通的完全积分单元相比在每个方向少了一个积分点，因此存在所谓的沙漏数值问题而过于柔软。沙漏问题指的是结构中某些部位因为应力集中而使其刚度明显下降。可以通过设置沙漏控制参数来克服沙漏问题，而且这种单元对于扭曲变形很大的模拟能够有很好的计算精度。因此混凝土选择C3D8R单元[8]。

(3)钢筋。钢筋采用T3D2单元。首先分别建立纵筋和箍筋的模型，然后将其合并成为一个新的部件(钢筋骨架)嵌入到混凝土中。这种方法能够对钢筋骨架准确定位，而且更加直观[9]。

(4)垫块。垫块同样采用C3D8R单元。为了防止应力集中，便于计算收敛设置了弹性垫块。通过设置垫块与混凝土的接触关系实现两者的变形协调[10]。

1.1.3边界条件

通过Interaction功能模块中的嵌入区域约束把钢筋嵌入混凝土中。弦杆和腹杆间采用绑定约束。T型钢刚度较大，是主面，角钢是从面。因为项目组前期试验采用的是两点对称加载。对于有限元分析软件ABAQUS来说，若对某点加载将会导致分析过程中不收敛，所以需要在加载点处设置两个垫块，为了防止应力集中在支座处也应该分别设置垫块。加载点和加载端之间采用耦合约束。因为本试验中垫块不是研究重点，所以假设以上垫块都是弹性钢垫块。

1.2试验介绍

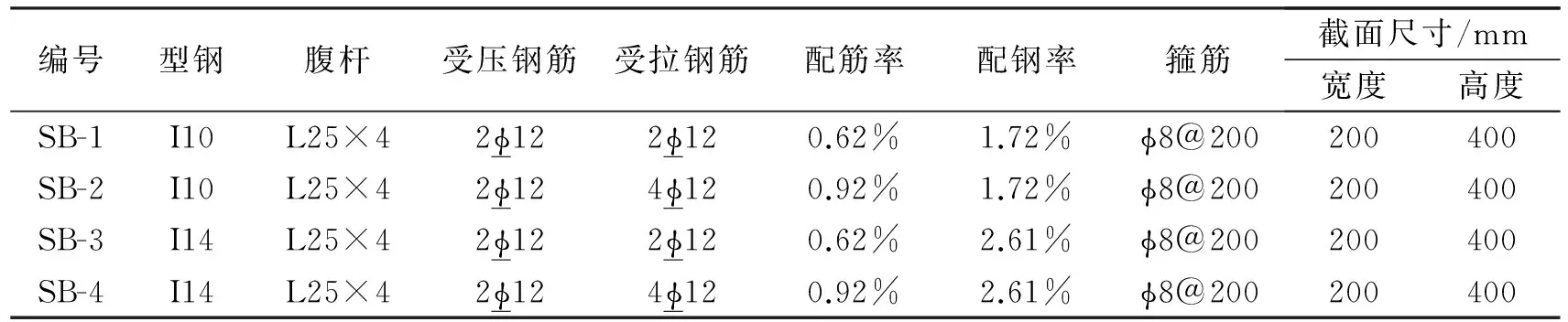
本文验证模型选用广西大学陆合勇[11]所进行的桁架式钢骨混凝土梁抗弯性能试验中构件号为SB-1—SB-4的梁，构件梁长为3 m，净跨为2.8 m，其中钢桁架是整体焊接而成。弦杆由普通工字形钢从中央剖开对称布置在梁两端，腹杆采用L25×4等边角钢。通过500 kN试验压力机对试件进行两点加载。荷载首先通过油压千斤顶传给分配梁，然后通过分配梁对试件实现两点加载。试件构造与尺寸见图1、图2和图3，试验加载装置见图4，试件的设计参数见表1，材料力学指标见表2和表3。

图1　钢筋布置图

图2　钢桁架布置图

图3　构件梁横截面图

图4　试验加载图

编号型钢腹杆受压钢筋受拉钢筋配筋率配钢率箍筋截面尺寸/mm宽度高度SB-1I10L25×42ϕ122ϕ120.62%1.72%ϕ8@200200400SB-2I10L25×42ϕ124ϕ120.92%1.72%ϕ8@200200400SB-3I14L25×42ϕ122ϕ120.62%2.61%ϕ8@200200400SB-4I14L25×42ϕ124ϕ120.92%2.61%ϕ8@200200400

表2　混凝土的力学指标

表3　钢材的力学指标

1.3有限元结果与试验结果对比

利用有限元软件ABAQUS对4根桁架式钢骨混凝土梁进行有限元分析，分别从型钢受力特征、荷载-位移曲线两个方面与试验结果进行对比。

1.3.1型钢骨架受力特征

由表4可知，在极限状态时上部型钢翼缘、上部型钢腹板和下部型钢翼缘有限元模拟应变值与试验值相比误差较小，表明了有限元分析的合理性。

表4　极限荷载下应变结果对比表　　　　　　(×10-6)

1.3.2荷载-位移曲线

由图5可知，曲线没有模拟出荷载-位移下降段，这是因为试件破坏后，型钢骨架仍然具有一定的承载力，因此荷载没有明显下降段。但是从图中可知随着荷载的不断增大，荷载增加幅度越来越小，最后趋于平缓。图中出现了一段随着位移的增加荷载几乎不变的屈服平台。因此可以通过屈服平台判断极限荷载值。如表5所示，模拟值与试验值相比存在一定的误差，误差平均值为0.45%，吻合度良好。误差产生的原因一方面可能与钢筋和型钢材料力学性能试验的结果存在误差有关，另一方面可能是因为没有准确模拟钢筋、型钢和混凝土之间的粘结滑移关系。

图5　荷载-位移曲线对比图

内容模拟值/kN试验值/kN误差/%SB-1207.67221.38-6.2SB-2290.71301.54-3.6SB-3263.92248.51+6.2SB-4353.52335.47+5.4

2　斜腹杆面积对抗弯极限承载力的影响

设计了10组截面尺寸都为200 mm×400 mm不同配钢率和不同配筋率的矩形截面构件梁，通过改变斜腹杆与型钢下弦杆面积的比值讨论斜腹杆面积对抗弯极限承载力的影响。试件的设计参数如表6所示。

表6　试件设计参数

有限元分析结果见表7，根据模拟结果讨论斜腹杆面积对构件抗弯极限承载力的影响。

表7　有限元模拟结果

注：面积比是腹杆面积与下弦杆面积的比值，弯矩比是面积比非零所对应的极限弯矩与面积比为0所对应的极限弯矩的比值。

由图6可知，对于截面形式是矩形的桁架式钢骨混凝土梁来说，当腹杆面积为0时构件梁的抗弯极限承载力最小，随着腹杆面积的增大，构件梁抗弯极限承载力逐渐增大。

图6　斜腹杆对抗弯极限承载力影响图

3　考虑斜腹杆面积影响的抗弯极限承载力计算公式推导

3.1抗弯极限承载力公式推导

根据上节有限元分析结果发现斜腹杆面积对抗弯极限承载力有影响，随着斜腹杆与下弦杆面积比值的增加抗弯极限承载力越来越大。因此考虑斜腹杆作用的抗弯极限承载力计算公式的推导可以采用如下的方法：

图7　斜腹杆面积比对抗弯极限承载力影响图

首先不考虑斜腹杆的作用，将型钢看作纵筋按照钢筋混凝土设计原理推导抗弯极限承载力Mu，然后乘以腹杆面积增大系数，就可以得到修正后的Muz。

为了研究斜腹杆对矩形截面桁架式钢骨混凝土梁的影响，一共设计了10组构件，每组构件有4根梁，4根梁除了腹杆面积逐渐增大外其他条件完全相同，通过上节分析可知腹杆面积比对构件抗弯极限承载力有影响(如图7)。将这10组构件的有限元分析结果进行数据拟合可以得到腹杆面积增大系数K0。因为10组构件梁腹杆与下弦杆面积的比值A0/A1<0.5，因此所建立的公式有一定的适用条件：

3.2计算值与试验值对比分析

由表8可知，对10根矩形截面桁架式钢骨混凝土梁抗弯极限承载力的试验结果Mue和公式计算结果Muz进行比较，Mue/Muz平均值为1.01，标准差为0.05，变异系数为0.05。修正后的计算值与试验值吻合度良好，说明本文建立的公式是合理的。

表8　抗弯极限承载力试验值与公式计算值比较

4　结　论

本文首先对桁架式钢骨混凝土梁一次受力进行有限元分析，通过课题组已有试验数据验证，有限元分析软件ABAQUS所建立的模型是正确的。因为课题组提出的抗弯极限承载力计算公式没有考虑斜腹杆的作用，所以导致公式计算值普遍小于试验值。本文通过改变斜腹杆与下弦杆面积的比值讨论斜腹杆对构件梁抗弯极限承载力的影响，得到如下结论：

(1)随着斜腹杆面积的增大，构件梁抗弯极限承载力逐渐增大；

(2)提出考虑斜腹杆作用的系数K0，将经过修正的抗弯极限承载力计算值与试验值进行比较，结果显示吻合度良好，说明本文建立的考虑斜腹杆作用的抗弯极限承载力计算公式是合理的。

[1]平振东.型钢混凝土结构在国内外的研究及工程应用[J].工程结构,2009,29(9):195-197.

[2]THANYAWAT P,PATTAMAD P.Modeling of mechanical bond-slip for steel-reinforced concrete under thermal loads[J].Engineering structures,2013,48(12):497-507.

[3]任君,杜洋,陈永庆.钢骨混凝土构件受力性能研究综述[J].建筑结构,2008,9(59):13-15.

[4]SERRA E, ROMERO M L. Influence of ultra-high strength infill in slender concrete-filled steel tubular columns[J].Journal of Constructional Steel Research,2013,86(7):107-114.

[5]中华人民共和国行业标准.混凝土结构设计规范:GB50010—2010[S].北京:中国建筑工业出版社,2010.

[6]过镇海,时旭东.钢筋混凝土原理和分析[M].北京:清华大学出版社,2003.

[7]张国丽,苏军.基于ABAQUS的钢筋混凝土非线性分析[J].科学技术与工程,2008,8(2):5620-5624.

[8]罗文,谢孝.钢筋混凝土梁非线性有限元分析[J].建筑与结构设计,2012,7(6):71-75.

[9]王建波,贾金青.预应力钢骨超强混凝土梁抗弯性能非线性分析[J].水利与建筑工程,2012,5(4):45-49.

[10]江见鲸,陆新征,叶列平.混凝土结构有限元分析[M].北京:清华大学出版社,2005.

[11]陆合勇.桁架式钢骨混凝土梁抗弯性能试验研究[D].南宁:广西大学,2012:5-17.

[责任编辑：魏 强]

Calculation on ultimate flexural bearing capacity of the reinforced concrete beam with steel truss

ZHAO Wen-xia1,DENG Zhi-heng2

(1.Experimental Center, Dalian Institute of Science and Technology, Dalian 116052, China;2.College of Civil Engineering and Architecture, Guangxi University, Nanning 530004, China)

Based on the force analysis of the reinforced concrete beam with steel truss by ABAQUS, and compared with the experiment results, the simulation matches well with experiments, which proves the feasibility of the finite element analysis. Some changes are made about the area of the oblique abdominal rod to discuss the influence on ultimate bearing capacity. It shows that the ultimate bearing capacity is increased gradually with the increase of the oblique abdominal rod.. Through the simulation results, the formula of ultimate flexural bearing capacity of the reinforced concrete beam with steel truss are derived when the oblique abdominal rod is considered. The revised calculation results are compared with experiment results, and it shows that calculation precision is greatly improved.

reinforced concrete beam with steel truss;finite element analysis;oblique abdominal rod;calculation of ultimate flexural bearing capacity

1673-2944(2016)05-0043-09

2016-05-31

2016-07-26

国家自然科学基金资助项目(51268005)

赵文霞(1988—)，女，满族，辽宁省大连市人，大连科技学院助理实验师，硕士，主要研究方向为结构设计；邓志恒(1963—)，男，广西壮族自治区灵川县人，广西大学教授，博士生导师，主要研究方向为高层建筑结构控制及抗震、混凝土及预应力混凝土结构。

TU398

A