电动汽车充电站选址定容优化策略探讨

周　敏，李　淼，周　泳

(1.国网四川省电力公司技能培训中心，四川 成都　610072；2.国网眉山供电公司客户服务中心，四川 眉山　620010)



电动汽车充电站选址定容优化策略探讨

周敏1，李淼1，周泳2

(1.国网四川省电力公司技能培训中心，四川 成都610072；2.国网眉山供电公司客户服务中心，四川 眉山620010)

积极发展电动汽车对保障能源安全、实施节能减排、全面推动经济增长方式的转变有着举足轻重的战略意义。但目前中国充电站选址与用户需求不协调以及配套保障措施不到位等原因限制了其发展与推广速度。针对上述问题，利用免疫算法优化了充电站的选址定容问题，为电动汽车的推广战略提出了有效借鉴。

电动汽车；充电站；选址定容

0　引　言

电动汽车是以车载电源为动力，用电机驱动车辆行驶的汽车，根据GB/T 19596-2004《电动汽车术语》，电动汽车可划分为纯电动汽车(battery electric vehicle，BEV)、燃料电池汽车(fuel cell electric vehicle，FCEV)、混合动力汽车(hybrid electric vehicle，HEV)等。积极发展电动汽车对保障能源安全、实施节能减排、全面推动经济增长方式的转变有着举足轻重的战略意义[1]。

目前，国家电网公司本着“主导快充、兼顾慢充、引导换电、经济实用”的原则，重点对公共服务领域的纯电动汽车推广应用给予充换电网络的配套支持。中国在电动汽车产业及其充电设施基础配套产业方面已经取得了相当瞩目的成就，但目前已建成的各类充换电站大多以电动公交车、电动环卫车、政府部门试点用车为主，充电网络服务能力和服务水平远远难以满足即将到来的大量且分散的私家电动汽车的充电需求。因此，要想促进中国电动汽车的推广与发展，必须优先发展电动汽车充电站的服务水平，不仅要增加充电站数量，而且要尽快提升充电站的运营服务水平。另外，充电站的选址需要给电动汽车用户提供最大限度的便利性、经济性和满意度。

充电站的选址需要有适合的服务半径，并考虑周边的电动汽车分布数量，尽可能降低与用户间的路径长度。故建立以用户到充电站进行充电路程及时间消耗最小的经济指标为主要考虑的数学模型，为充电站选址提供优化策略。

1　充电站选址定容优化策略

1.1用户充电路径最短的充电站选址定容数学模型

由于实际情况下电动汽车用户数量众多，城市地理结构复杂，在缺少详细数据的情况下对充电站的选址数学模型进行适当的简化，首先作出如下3点假设：

1)将用户集中的区域(如一个小区或办公区域)的所有用户的地理位置设为所在地的中心；

2)各个区域用户数量处于实时变动，为了确定充电站的最优位置和容量，假设各个区域的用户数量和需求保持不变；

3)由于城市路况的复杂性，在缺少所有道路信息以及实时交通流量信息的情况下，假设用户到充电站的路径长度与其空间直线距离成正比。

其次基于假设建立一个充电站优化选址模型，在满足距离上限的情况下，需要从N个模拟用户位置中找出最合适的作为充电站的地址。该模型使得各个用户模拟点中的用户总量与其到最近充电站的路程长度的乘积之和最小，并且每个充电站的充电容量能满足最近用户的充电需求。模型数学描述如式(1)～式(5)所示。

目标函数为用户最小充电路径总长最小：

minF=min(Ploss(Pline1,Pline2,…,PlineN))

(1)

约束条件为

(2)

Zij≤hj(i∈N,j∈Mi)

(3)

Zij,hj∈{0,1}(i∈N,j∈Mi)

(4)

系统运行时能量供需平衡

(5)

式(1)至式(5)中：PL为电动汽车用户所需的总充电功率；Pdg是各充电站所能够提供的总充电功率；N为模拟用户点个数；M为拟建设的充电站个数iN，M⊆N；dij表示从用户i到最近的充电站的线路长度；Zij为0-1的变量，表示用户和充电站之间的服务需求分配关系，当其为1时，表示用户i的需求量由充电站j来提供，否则Zij=0。

1.2基于免疫算法的充电站优化选址方法

1.2.1免疫算法概述

上节中建立的充电站选址优化的数学模型是一个非凸和非光滑且拥有复杂约束条件的非线性规划模型，属于NP-hard问题，用传统数学方法无法对其直接求解。这里采用免疫优化算法对其求解并进行了经济性分析。

1.2.2免疫算法优化流程

免疫算法的求解流程如图1所示。

免疫算法的概念与充电站选址定容优化问题的对应关系如表1所示。

结合图1所示的免疫算法求解流程和表1描述的免疫算法概念与充电站选址问题的对应关系可以确定算法的具体实现步骤如下所示：

图1　免疫算法流程图

免疫算法充电站选址定容抗原用户位置编码抗体充电站选址方案(安置点序列)抗体与抗体之间的亲和力充电站选址方案中位置相同的个数比例记忆细胞充电站选址方案的可行解

1)初始抗体群的产生。若记忆库非空，则初始抗体群从记忆库中选择生成；否则，在可行解空间随机产生初始抗体群。所提免疫算法抗体编码采用简单编码方式，每个充电站选址方案可形成一个长度为p的抗体(p表示充电站的数量)，每个抗体代表被选为充电站安置点的序列。例如，考虑整个区域包含31个集中模拟需充电用户以及6个充电站的情况，则1，2，…，31代表用户的序号，从中选出6个点作为充电站的安置地点。抗体[2 8 15 23 29 18]代表一个可行解，它表示编号2、8、15、23、29、18的地址被选为充电站的安置地点。这种编码方式能够满足约束条件式(2)。

2)解的多样性分析。解的适应度计算包括有抗体与抗原间的亲和力计算、抗体与抗体间亲和力计算、抗体浓度计算以及期望繁殖概率计算。

抗体与抗原间的亲和力表示抗体对抗原的识别程度，此处针对上述充电站选址定容数学模型设计亲和力函数Av。

(6)

式中Fv为目标函数；分母中的第二项表示对违反距离约束的充电站选址位置解给予惩罚，B取一个比较大的正数。

抗体与抗体之间的亲和力反映了不同抗体之间的相似程度。采用变形的R位连续方法来计算抗体与抗体之间的亲和力，在不考虑编码次序的情况下若两种抗体编码有超过R位相同，则认为2种抗体“相同”，否则认为两种个体不同。这里R为亲和力判定的阈值，即：

(7)式中：L表示抗体的总长度；kv,s表示抗体v与抗体s中相同编码的数目。例如，2个抗体即2个充电站选址方案为[2 7 15 21 5 11]、[15 8 14 26 5 2]，经比较，有3个值是相同的，即L=3。充电站总数为6，即L=6。此时可计算出抗体与抗体之间的亲和度为0.5，即比较的2个充电站选址方案的相似度为50%。

抗体的浓度Cv表示群体中相似比例高于T的充电站选址方案所占的比例，即：

(8)

(9)

式中：N为抗体总数；T为预先设定的一个阈值。

所设计的免疫算法中个体的评价标准是期望繁殖率P，是由抗体浓度Cv以及抗体与抗原间亲和力Av两个部分共同决定，具体计算如式(10)所示。

(10)

式中，α为常数。由式(10)可知，期望繁殖概率P与个体适应度成正比；期望繁殖概率P与个体浓度成反比。这样就能够同时鼓励适应度高的个体并且抑制浓度高的个体，从而保证个体的多样性。

3)免疫操作。主要将初始计算得到的充电站选址方案通过选择、交叉、变异产生的免疫操作并结合从记忆库中取出记忆的个体，共同构成新的充电站选址方案。新产生的充电站选址方案再经过多样性分析这一过程进行迭代，最终经过多次迭代之后获得最优方案。

2　基于免疫算法的充电站选址方法仿真分析

2.1算例介绍

本算例设计一个含有多个充电站和集中用户的区域，区域中总共拥有31个模拟集中用户和6个充电站，每个集中用户的大小和位置都已知。空间整体规模为长宽各4 500 m，其空间坐标位置和需求量如表2所示，表中列出了算例设置的31个集中用户的位置以及容量参数。用户坐标是为了方便表述用户的位置以及计算充电站与用户之间的线路长度而设定，单位为m。

在Matlab中编程实现算例城市区域中的充电站选址定容优化。免疫算法中：种群规模设为50，记忆库容量设为10，迭代次数设为100，交叉概率设为0.5，多样性评价参数设为0.95，变异概率设为0.4。

2.2仿真结果与经济性分析

表2　模拟城市区域内用户的空间坐标及大小

免疫算法搜索过程如图2所示。充电站的选址定容方案如图3所示。

图2　免疫算法收敛曲线

由图2可知，该算法不仅是收敛的，而且在迭代40次后便搜索到了最优解。

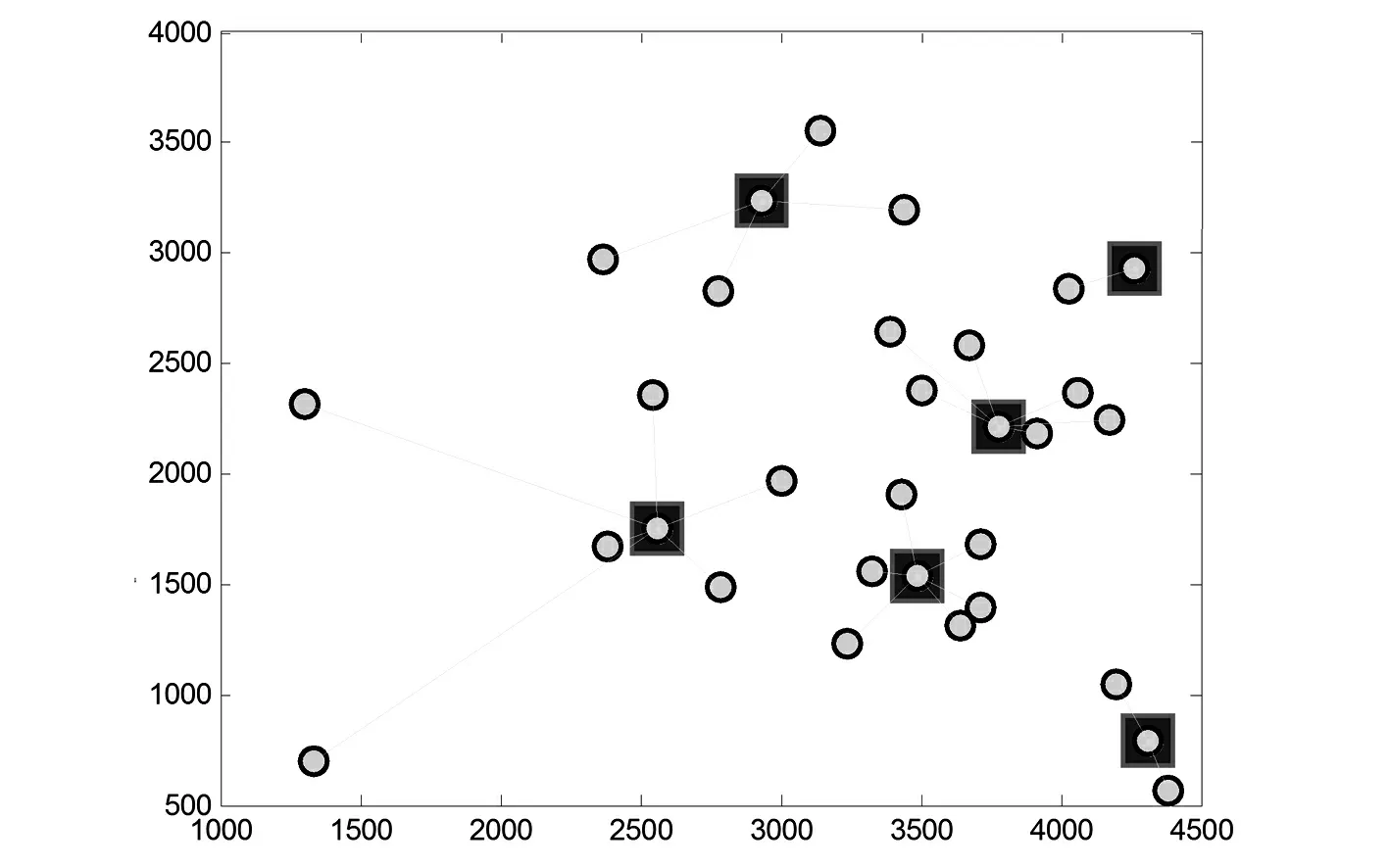
图3　充电站选址方案

图3中，圆形点表示用户的分布位置，方框包围的点表示充电站的配置地点，点与点之间的连线则表示该用户由其所连接的充电站进行供电。优化后充电站选址定容方案的具体参数如表3所示。

表3　充电站选址定容方案

表3中充电站序号/用户序号表示充电站放置的地点。例如，第一个充电站的选址定容优化方案为放置位置位于序号为6的用户处，空间坐标为(3 326，1 556)，容量大小为196 kW。

为了分析所设计的基于免疫优化算法的充电站配置优化方法是否能够减少用户到充电站之间的距离，以提高经济效率，首先计算了免疫算法优化后的用户充电路程总长度，再用同样的方法计算未优化选址方案的用户充电路程总长度，最后进行比较分析得出结论。

1)免疫算法优化后用户充电线路总长度及加权值

根据表2和表3可以得出各个充电站与各个用户之间的线路长度以及其总损耗大小，如表4所示。

表4中，线路编号代表该线路连接哪两个用户和充电站，例如编号1-14的线路代表线路连接的是处于14位置的充电站和1号用户，线路的长度为1 190 m，1号用户所需电能为8 kW；加权值由线路长度和用户所需电量决定，表示该用户的总损耗值。其余含义以此类推。

2)未优化情况下用户充电线路总长度及加权值

将6个充电站均放置在算例区域中31个用户包围的中心附近位置进行计算，这里设定充电站均放置于(2 250，2 000)处。计算结果如表5所示。

表5中数字含义与表4一致。

由表5计算结果可知，充电站置于区域中心位置时，充电线路总长度为44 090 m，加权值为1 156 176。

3)充电站选址定容优化的经济性分析

充电站选址优化的目标函数是用户充电路径总长最小，优化前后的详细经济性对比如表6所示。

由表6可知，充电站的位置和容量配置经过免疫算法优化后，用户充电线路总长减少了74.2%，加权值减少了78.3%，这表明充电站选址优化后电动汽车用户能够大大减少去往充电站的路径，节约了大量的时间，经济效应明显。

3　结　语

首先介绍了电动汽车的优势与推广的必要性，并针对中国现有充电网络服务能力难以满足即将到来的大量且分散的私家电动汽车的充电需求问题，提出了充电站选址定容优化策略，归纳了充电路径最短的充电站选址数学模型，并提出运用免疫算法对模型进行求解的方法。最后通过设置算例并仿真验证了算法的有效性。从企业、政府角度为电动汽车的推广战略提出了有效的技术借鉴。

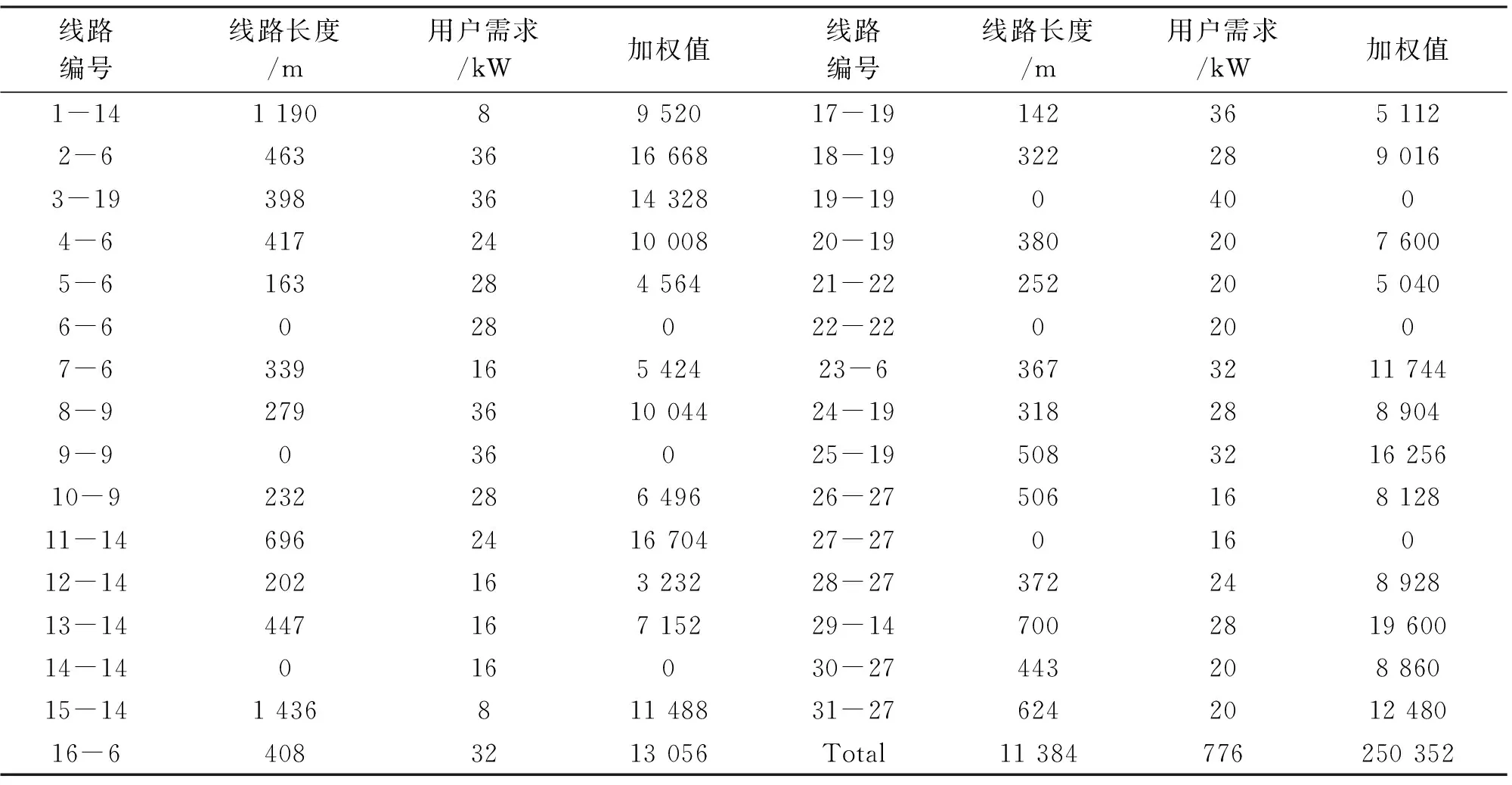
表4　优化后配置充电站与用户间线路长度及加权值

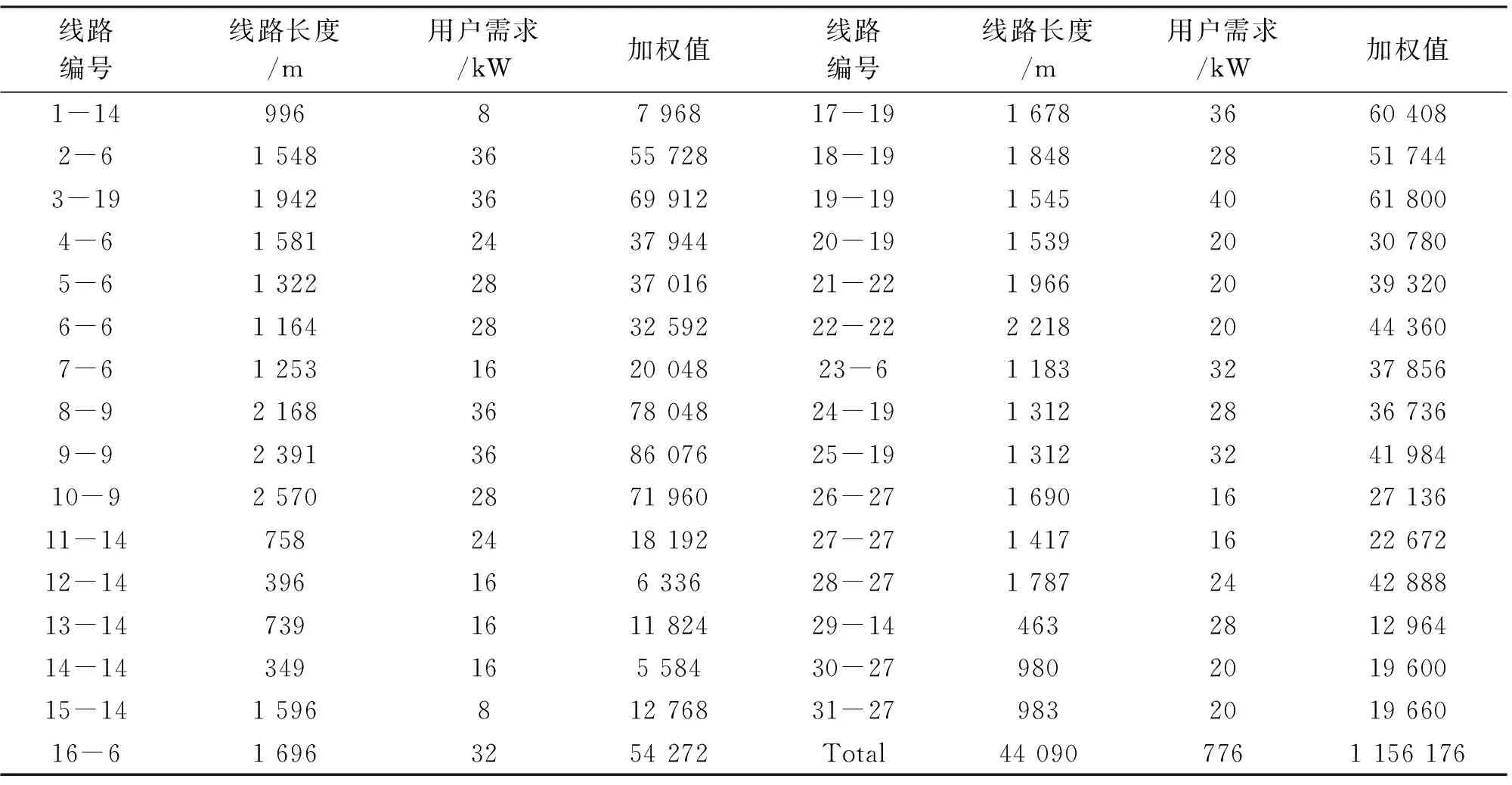
表5　充电站置于区域中心时的线路长度及加权值

表6　免疫算法优化的经济性分析

[1]胡泽春,宋永华,徐智威,等. 电动汽车接入电网的影响与利用[J]. 中国电机工程学报,2012,32(4):1-10.

[2]徐智威,胡泽春,宋永华,等. 充电站内电动汽车有序充电策略[J]. 电力系统自动化,2012,36(11):38-43.

[3]宋永华,阳岳希,胡泽春. 电动汽车电池的现状及发展趋势[J]. 电网技术,2011,35(4):1-7.

[4]李岩. 智能电网中电动汽车参与微网联合运行的关键技术研究[D].沈阳：东北大学,2013.

[5]马滨滨. 论我国电动汽车的推广策略[D].厦门：厦门大学,2014.

Positive development of electric vehicles has a decisive strategic significance to ensure the energy security, implement the energy-saving emission reduction and promote the transformation of economic growth mode. But at present, because the location selection of charging stations in China is not coordinated with user needs and the supporting security measures are far from satisfactory, it limits the speed of its development and promotion. In view of the above problems, the immune algorithm is used to optimize the location and capacity selection of the charging stations, which provides an effective reference for the promotion strategy of electric vehicles.

electric vehicle; charging station; location and capacity selection

TM715

A

1003-6954(2016)04-0045-05

2016-02-15)