刚重比在高层建筑钢结构中的应用
王迎春 (安徽省建筑科学研究设计院,安徽 合肥 230001)
刚重比在高层建筑钢结构中的应用
王迎春(安徽省建筑科学研究设计院,安徽合肥230001)
钢结构在高层建筑中的使用越来越多,高层钢结构建筑的整体稳定性设计显得尤为重要。在高层钢结构中,刚重比作为反映整体稳定性一个重要参数,也应该得到有效保证。
高层钢结构;整体稳定性;刚重比
0 前言
结构的侧向刚度和重力荷载之比即“刚重比”,刚重比作为反映整体稳定性一个重要参数,其在《高层建筑混凝土结构技术规程》(下文简称高规)5.4.4条有要求,《钢结构设计规范》(下文简称钢规)、《建筑抗震设计规范》(下文简称抗规)以及《高层民用建筑钢结构技术规程》(下文简称高钢规)中没有刚重比限值的直接要求。《高钢规》5.2.10条要求的整体稳定,在现行软件计算书中未有体现。如何控制高层钢结构的整体稳定性至关重要。
1 刚重比的表达形式
“刚重比”是指结构的侧向刚度和重力荷载之比,《高规》5.4.4条高层建筑结构的整体稳定性应符合下列规定。
剪力墙结构、框架-剪力墙结构、简体结构应符合下式要求:
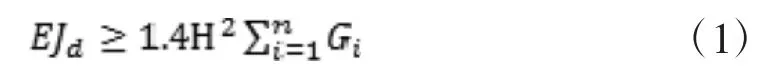
框架结构应符合下式要求:
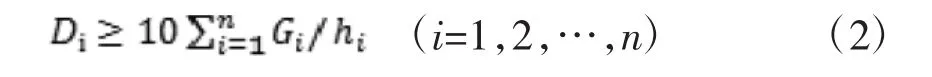
2 刚重比的意义
可以结合《高规》5.4.1条来理解。《高规》5.4.1条文以及条文说明如下:当高层建筑结构满足下列规定时,弹性计算分析时可不考虑重力二阶效应的不利影响。
剪力墙结构、框架-剪力墙结构、板柱剪力墙结构、简体结构:

框架结构:
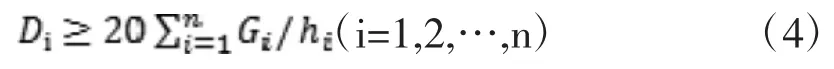
式中:EJd为结构一个主轴方向的弹性等效侧向刚度,可按倒三角形分布荷载作用下结构顶点位移相等的原则,将结构的侧向刚度折算为竖向悬臂受弯构件的等效侧向刚度;H为房屋高度;Gi、Gj分别为第i、j楼层重力荷载设计值;hi为第i楼层层高;Di为第i楼层的弹性等效侧向刚度,可取该层剪力与层间位移的比值;n为结构计算总层数。
条文说明5.4.4结构整体稳定性是高层建筑结构设计的基本要求。研究表明,高层建筑混凝土结构仅在竖向重力荷载作用下产生整体失稳的可能性很小。高层建筑结构的稳定设计主要是控制在风荷载或水平地震作用下,重力荷载产生的二阶效应不致过大,以免引起结构的失稳倒塌。结构的刚度和重力荷载之比(刚重比)是影响重力P-△效应的主要参数。如结构的刚重比满足公式(1)或(2)的规定,则在考虑结构弹性刚度折减50%的情况下,重力P-△效应仍可控制在20%之内,结构的稳定具有适宜的安全储备。若结构的刚重比进一步减小,则重力P-△效应将会呈非线性关系急剧增长,直至引起结构的整体失稳。在水平力作用下,高层建筑结构的稳定应满足本条的规定,不应再放松要求。如不满足本条的规定,应调整并增大结构的侧向刚度。
当结构的设计水平力较小,如计算的楼层剪重比(楼层剪力与其上各层重力荷载代表值之和的比值)小于0.02时,结构刚度虽能满足水平位移限值要求,但往往不能满足本条规定的稳定要求。
条文说明5.4.1在水平力作用下,带有剪力墙或简体的高层建筑结构的变形形态为弯剪型,框架结构的变形形态为剪切型。计算分析表明,重力荷载在水平作用位移效应上引起的二阶效应 (重力P-△效应)有时比较严重。对混凝土结构,随着结构刚度的降低,重力二阶效应的不利影响呈非线性增长。因此,对结构的弹性刚度和重力荷载作用的关系应加以限制。本条公式使结构按弹性分析的二阶效应对结构内力、位移的增量控制在5%左右;考虑实际刚度折减50%时,结构内力增量控制在10%以内。如果结构满足本条要求,重力二阶效应的影响相对较小,可忽略不计。
从上述《高规》5.4.1条文以及条文说明论述可以看出,刚重比之所以可以表示结构的整体稳定性,是从控制结构的重力P-△效应在一定范围内来入手的。混凝土结构中,考虑了的混凝土的开裂引起的结构刚度折减50%。
以框架结构为例,简单推导一下刚重比限值的含义。
则式(2)、(4)可以转化为:
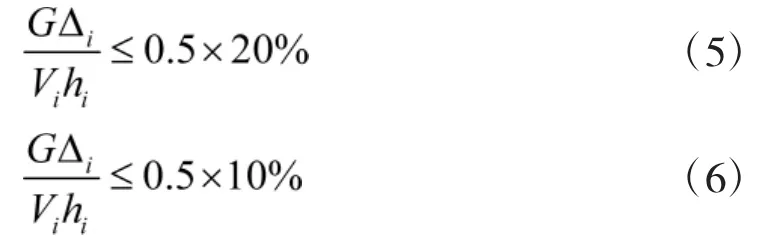
可以看出,Vihi表示水平剪力作用在楼层高度上的弯矩,主要的结构弯矩;表示上部重量作用在侧移上的附加弯矩,也就重力P-△效应。式(5)、(6)就是控制该比例在10%(5.4.4条验算刚重比也就是整体稳定时)和5%(5.4.1条验算是否考虑二阶效应时)。
3 刚重比在高层钢结构中如何保证
在高层钢结构中,刚重比作为反映整体稳定性一个重要参数,也应该得到有效保证。如果直接采用《高规》中的公式5.4.4,则应注意钢结构不用考虑刚度折减50%,因为这项折减是考虑了混凝土的开裂才引入的。从理论上讲,高层钢结构的整体稳定性应符合下列规定。
剪力墙结构、框架-剪力墙结构、简体结构应符合下式要求:
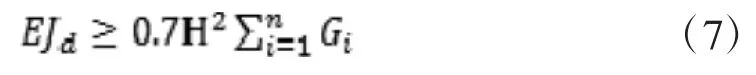
框架结构应符合下式要求:
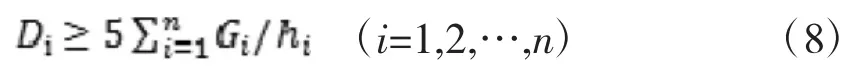
这一点可以从《钢规》3.2.8条得到印证。
《钢规》3.2.8条:框架结构内力分析宜符合下列规定:
框架结构可采用一阶弹性分析。

式中:Qi为第i楼层的总重力荷载设计值;ns为框架总层数,当时,取此根号值为1.0;ay为钢材强度影响系数,其值:Q235钢为1.0、Q345钢为1.1、Q390钢为1.2、Q420钢为1.25。
对无支撑的纯框架结构,当采用二阶弹性分析时,各杆件杆端的弯矩MⅡ可用下列近似公式进行计算。

式中:MIb为假定框架无侧移时按一阶弹性分析求得的各杆件端弯矩;MIs为框架各节点侧移时按一阶弹性分析求得的杆件端弯矩;a2i为考虑二阶效应第i层杆件的侧移弯矩增大系数;∑N为所计算楼层各柱轴心压力设计值之和;∑H为产生层间侧移△u的所计算楼层及以上各层的水平力之和;△u为按一阶弹性分析求得的所计算楼层的层间侧移,当确定是否采用二阶弹性分析时,△u可近似采用层间相对位移的容许值[△u],[△u]见本规范附录A第A.2节;h为所计算楼层的高度。
《钢规》3.2.8注:①当按本文公式(11)计算的a2i>1.33时,宜增大框架结构的刚度。
②本条规定不适用于山形门式刚架或其他类似的结构以及按本规范第9章进行塑性设计的框架结构。
以框架结构为例,从物理意义上,《钢规》3.2.8中的与《高规》中一致。可以看出,《钢规》中当时才考虑二阶效应的计算,而《高规》中针对混凝土结构就要考虑二阶效应了。可见,钢结构比混凝土结构要求要低,这是有钢结构的强度高、延性好等特性决定的。
再看《钢规》3.2.8下面的注1:当α2i>1.33,也就是才通过增加结构刚度或体系来保证整体稳定性,在0.1~0.25之间都可以通过考虑二阶效应来解决,不用改变结构。《高规》中混凝土结构中该值为0.1(见5.4.4条文说明)。
4 结 论
综上所述,钢结构的刚重比如果采用《高规》5.4.4中的参数表达,则可以放宽至其取值的一半,甚至0.4倍。这一结论,可以与现行计算软件的刚重比计算值做相应对比,予以参考并判定结构的整体稳定性。刚重比仅有一点不足,高层钢结构的整体稳定性问题应该不大。
[1]GB50017-2003,钢结构设计规范[S].
[2]GB5011-2010,建筑抗震设计规范[S].
[3]JGJ99-98,高层民用建筑钢结构技术规程[S].
[4]JGJ3-2010,高层建筑混凝土结构技术规程[S].
TU311.4
B
1007-7359(2016)04-0127-02
10.16330/j.cnki.1007-7359.2016.04.051
王迎春(1984-),男,安徽怀远人,毕业于安徽建筑大学,学士,工程师。

