波导实现数字逻辑回路及信号输出特性分析

崔 浩，冯 浩，李现伟

（1.中国石油大学胜利学院，山东东营 257061； 2.宿州学院，安徽宿州 234000；3.早稻田大学国际情报通信研究科，日本东京 169-8050）

波导实现数字逻辑回路及信号输出特性分析

崔 浩1，冯 浩2，李现伟3

（1.中国石油大学胜利学院，山东东营 257061； 2.宿州学院，安徽宿州 234000；3.早稻田大学国际情报通信研究科，日本东京 169-8050）

为了进一步改善R-SPP（正反馈表面等离子体激元）在非对称波导结构中的性能，设计了一种新型的平面型非对称波导结构。研究了入射角和波长取一定值时，传播距离函数导致的显著振荡特性，分析表明，该结构在核芯厚度一定时，能够通过改变入射角实现长距离的传播SPP模式，且在700～1 500 nm的入射波长下能够实现5～50μm的传播距离。通常传统的SPP的传播距离约为2μm，而该结构的最大传播距离可达50μm，这一结果对于SPP在新型光子器件中的推广应用有一定的理论和实际意义。

正反馈表面等离子体激元；非对称波导；表面等离子体激元模式

0 引 言

SPP（表面等离子体激元）是被短暂地局域在金属表面传播的电磁表面波。SPP在金属表面的传播距离应该尽可能长以适应于这些应用。增大传播距离的一种方法是将SPP耦合进波导结构中［1］。1981年，Sarid引入了LR（长程）-SPP模式的理念，这一开创性工作实现了电磁表面波在两个折射率相似的介质层中间的金属薄膜上的传导，Sarid团队同时还预测了超SPP传播长度能够实现长距离传播。一般情况下，当上下两个介质面的折射率相等或者在辐射损失的衰减值上接近时，就会出现最合适的结果。同时，在可接受的合理范围内，金属薄膜足够薄时，可以减少吸收率损失［2-3］。在此限制下，对于薄的金属薄膜来说，涉及到等离子激元的系统有两个TM（横磁）模式:对称模式和非对称模式［4］。通常在对称或者大致对称的金属薄膜介质层包层的情况下，人们会讨论LR-SPP［5］。本文基于这一背景是为了表明通过控制一系列较大的玻璃层厚度的值，传播长度和场强可以得到十分显著的提高。这一研究对于SPP在新型光子器件中的推广应用有一定的理论和实际意义。

1 结构设计与SPP激发分析

1.1 波导结构设计

设计结构如图1所示，与Kretschmann结构（下文简称“K结构”）激发SPP基本类似，只是在棱镜的另一面又连接了一层介质层。设计的ε3用来反射辐射损耗使其补偿SPP传播中的金属损耗，即启动了一个反馈效果。依据菲涅尔定律，在2层/3层（自上而下）界面上的反射光也能作为有相同角度的入射光。这就确保了被反射回金属的光反馈，形成谐振腔。为了反射所有的辐射光，折射光就不能进入3层，即在2层/3层界面上需要以相同角度发生全反射。设图1中入射光与表面的夹角为θSPP（即图中的θ），显然这个角度也是2层/3层界面上的反射角。因此，必须使为2层/3层的反射角），这样就能写出SPP传播的谐振。又由于θSPP≥，这就使得ε2＞max（ε1，ε3）。θSPP≥与K结构激发SPP条件基本类似，这样当ε1＜ε3＜ε2时，金属介电常数的实部（虚部）满足

如果ε1＜ε3＜ε2，它的范围与传统的情况相同:

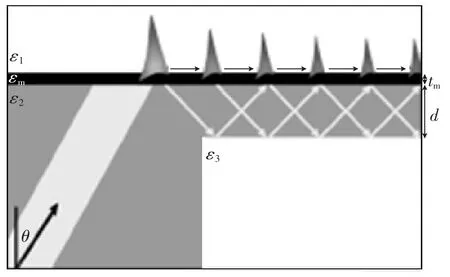
图1 本文设计的R-SPP结构

1.2 SPP传播分析

这里用总场-分散场方法引入一个入射光束，其角频率ω0与时间呈正弦曲线关系，对应的波长为λ0=2πc/ω0=532 nm。如图1所示，该光束以一定角度θ从玻璃侧入射到金属薄膜上，并且有一垂直于其传播方向的4μm的高斯空间分布。θSPP为光通过动量匹配有效地耦合至银-空气界面上的SPP时的角度的估值，我们取θ=θSPP=45°。

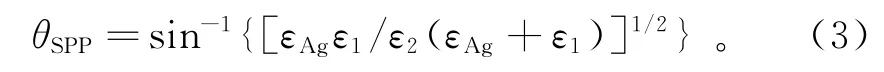
为了与Drude模型取得一致，引入关于金属银的介电常数εAg（ω）的辅助差分方程:

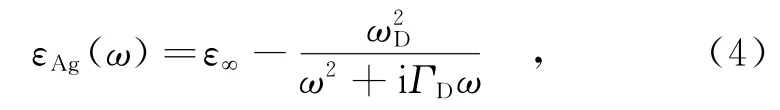
式中，ε∞=4.168 3；共振频率ωD=1.340 2× 1014Hz；反射光频率ΓD=2.126 4×1014Hz。当ω=ω0、λ0=532 n m时，εAg的理论值为εAg= -10.1+i0.84。

入射光束连续传播150 fs时，其时间长到足以产生一个“稳态”对应于入射频率ω0。在FDTD（有限差分时域）运算中，E（x，y，t）=Re｛Ec（x，y）exp（-iω0t）｝，式中，E（x，y，t）和Ec（x，y）分别表示一般电场强度和本文的反射光电场强度，这就意味着（实际的）电场矢量以时间重复性的方式变化，与入射波的频域复向量保持一致，从而求解麦克斯韦方程组。如果在层1和金属界面附近存在SPP传播，对于一个恰好在金属表面上方的不变值y，横轴（）和纵轴（）的向量分量都会随exp（i kxx）中的x的变化而变化，其中复数kx=β+iα为传播常数，虚部α对应于金属的能量吸收。随着x值的增大，电场强度呈指数衰减:

式中，Lx=1/2α；φ为相位因子。对于距x轴一定距离的金属薄膜来说，通过时间平均强度〈|E|2〉t中的x值的变化可以确定Lx的值:

式中，τ为弛豫时间；T=2π/ω0。如果式（5）成立，那么式（6）应该随x的值呈指数形式衰减。因此，可以通过拟合时间平均强度与C exp（-x/Lx）相匹配来确定Lx的值。

2 数值分析

2.1 传播长度分析

我们绘制了取决于FDTD结果的R-SPP传播长度Lx（d）的曲线（此处d表示玻璃厚度），如图2所示。从图中可以观察到显著的振荡相关性，其最大值为44μm，最小值为5μm。为了便于比较，标准K结构中传播长度仅设置为Lx（d=∞）= 1.7μm，因此，根据导芯厚度，传播长度增加至30μm是可能的。

图2 传播长度Lx（d）的曲线图

2.2 玻璃核芯厚度变化影响分析

图3给出了传播长度随玻璃核芯厚度d变化的最终色散关系，用ω（β）表示。图中，kair和kglass所对应的实线分别为空气和玻璃的光谱线，水平实线对应ω0=3.542×1015Hz或者λ0=532 nm时的色散关系。很显然，随着d的增加，越来越多的模式变得可用，而且这些模式大部分位于空气（上层）和玻璃（下层）之间，因此，这些模式对应于空气-金属界面上的衰减模式。从图中还可以看出，无论在哪种情况下，总有一种模式的色散能够位于kglass曲线的下方（见图（b）～（e））。随着d的增加，这种模式更多的是与金属-玻璃界面上的衰减模式有关联（也就是玻璃面的SPP），而不是与空气面的传播常数有关。位于空气线和玻璃线之间的有关的TM模式分别用TM0、TM1、TM2…来标记，当ω一定时，有β（TM0）＞β（TM1）＞β（TM2）…。当d=0（见图（a）），即对应空气-金属-空气的情况时，应该考虑两种极限情况:在金属板的厚度极限值上有两个衰减TM模式，其代表值为tm=500 nm；在金属板的薄度极限值上，其代表值为tm=30 nm。这两个简并模式开始进行干扰和分裂，从而产生一个对称的LR-SPP模式（β值较小的情况）和一个短暂的非对称模式（β值较大的情况）。当d=210 nm时（见图（b）），在金属（实线）和玻璃亮线之间只存在模式TM0，对应于λ0=532 nm的那条水平线。然而，当d=518 n m时（见图（e）），空气线和玻璃线之间沿λ0=532 nm水平线有3种可能的模式:TM0、TM1和TM2。该种情况下，模式TM0（β值最大的情况）最靠近玻璃线，TM2最靠近空气线。

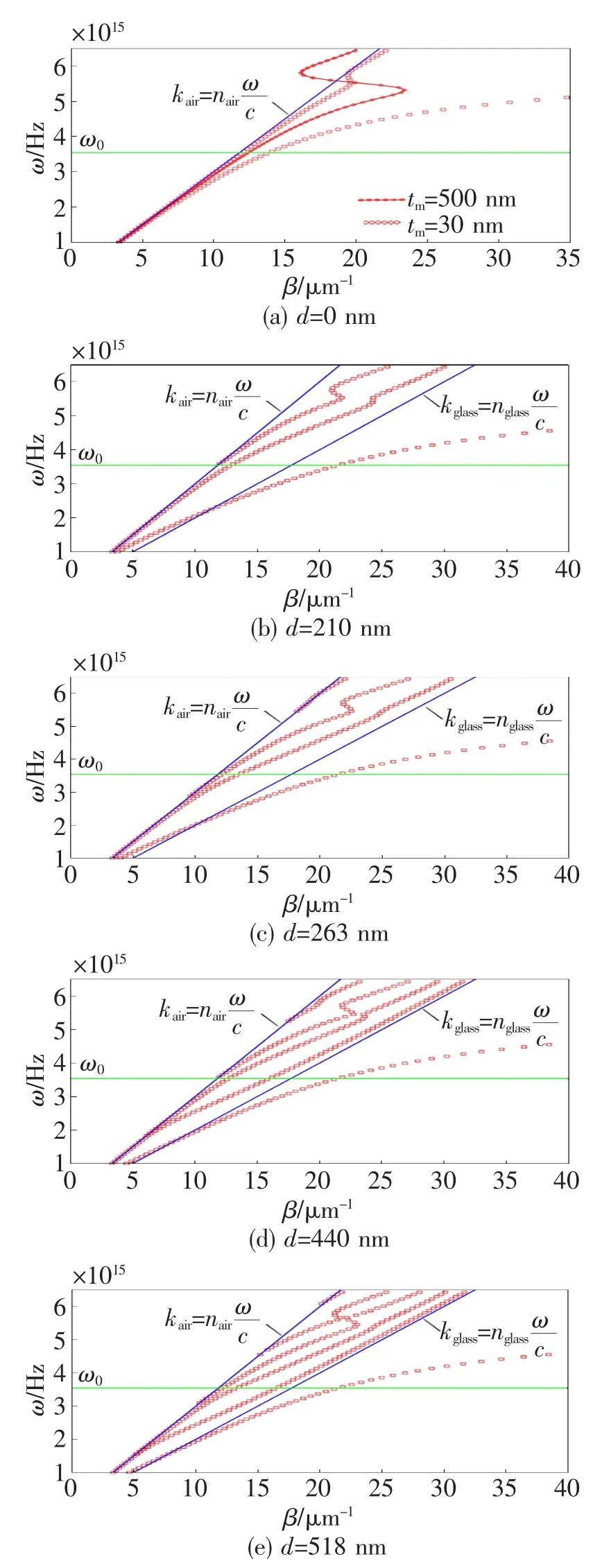
图3 色散曲线图

3 结束语

本文通过研究和分析R-SPP结构中有关SPP的传播增强，发现在不同的玻璃芯厚度d中SPP的传播长度Lx可以提高30倍。研究结果大大地扩展了传统的K结构传播SPP应用范围，能够通过改变入射角实现长距离的传播SPP模式。研究结果对于SPP在新型光子器件中的推广应用有一定的理论和实际意义。

［1］Zhu Ju，Qin Liuli，Song Shuxiang.Surface plasmon resonance demodulation by optical ring-down cavity technology［J］.Optik-International Journal for Light and Electron Optics，2016，127（3）:1207-1212.

［2］朱君，秦柳丽，傅得立，等.一种石墨烯波导褶皱激发表面等离子体激元的设计［J］.光子学报，2016，45（2）:224003.

［3］Mitchell A R.Studies in solid-phase peptide synthesis: A personal perspective［J］.Biopolymers:Original Research on Biomolecules and Biomolecular Assemblies，2008，90（3）:215-233.

［4］Marr M，Kuhn J，Metcalfe C，et al.Electrochemical performance of solid oxide fuel cells having electrolytes made by suspension and solution precursor plasma spraying［J］.Journal of Power Sources，2014，245（1）:398-405.

［5］Protsenko I E.Dipole nanolaser［J］.Physical Review A Atomic Molecular&Optical Physics，2005，71（1）:119-136.

Waveguide for Digital Logic Circuit and Signal Output Characteristic Analysis

CUI Hao1，FENG Hao2，LI Xian-wei3
（1.Sheng Li College，China University of Petroleum，Dongying 257061 China； 2.Suzhou University，Suzhou 234000，China；3.Global Information and Telecommunication Institute，Waseda University，Tokyo 169-8050，Japan）

In order to further improve the performance of positive feedback surface plasmas（R-SPP）in the asymmetric waveguide structure，we design a new type of planar asymmetric structure of waveguide in this paper.We study the oscillation characteristics of the propagation distance function under certain value of incident angle and wavelength.The analysis shows that long-distance transmission SPP mode can be achieved by changing the angle of incidence at the certain value of the thickness of the core.It is shown that 5 to 50μm propagation distance can be achieved under the incident wavelength of 700～1 500 nm range.It is noted that the traditional SPP propagation distance is limited to be about 2μm.However，the design of the structure can increase the maximum transmission distance up to 50μm.The results have certain theoretical and practical significances in the application of new photonic device based on SPP.

positive feedback surface plasmas；asymmetric waveguide；SPP mode

TN252

A

1005-8788（2016）05-0055-03

10.13756/j.gtxyj.2016.05.016

2016-04-25

国家自然科学基金资助项目（092000217）；中央高校基本科研业务费专项基金资助项目（14CX02175A）

崔浩（1979-），男，湖南益阳人。讲师，硕士研究生，主要从事高性能计算机研究。