阿基米德蜗轮齿面建模与计算

宋　丹,刘　君,晏克俊

(西安理工大学 机械与精密仪器工程学院,陕西 西安 710048)



阿基米德蜗轮齿面建模与计算

宋丹,刘君,晏克俊

(西安理工大学 机械与精密仪器工程学院,陕西 西安 710048)

本文基于阿基米德蜗轮蜗杆(ZA蜗轮蜗杆)的加工原理及蜗轮蜗杆空间啮合原理,推导出阿基米德蜗轮齿面数学模型及蜗轮蜗杆啮合方程式。在蜗轮轴截面方向进行齿面网格划分,根据蜗轮蜗杆啮合原理以及齿面网格节点空间坐标的数值关系建立非线性方程组。最后通过MATLAB求解出阿基米德蜗轮空间网格点的坐标值及法矢,并在三坐标测量机上验证了算法的可行性。

阿基米德蜗轮; 齿面数学模型; 网格划分; 三坐标测量机

蜗轮蜗杆作为一种重要的机械传动元件,广泛应用在机床、汽车、仪器、冶金等领域。然而在其加工过程中,由于机床加工参数的调整以及刀具的影响,存在一定的加工和安装误差,导致齿面存在一定的误差,误差对传动系统的精度与动态特性(特别是振动与噪声)有直接的影响[1]。因此,有必要研究蜗轮蜗杆的齿面模型,分析并构造蜗轮蜗杆的理论齿面,将齿面测量数据和理论齿面坐标值进行比较,从而得到齿面误差,并运用相关切齿修正理论和技术调整加工机床,可使加工出来的齿面更接近于理论齿面。

所以,如何获取的理论齿面数据就成为控制蜗轮蜗杆齿面精度的关键。天津大学王树人教授及美国的Faydor L.Litvin教授等对蜗杆传动的啮合理论及蜗轮蜗杆齿面建模进行了深入研究,为蜗杆传动提供了理论基础[2-3]。浙江大学李立新等以双三次B样条插值曲面反算方法为基础,计算出蜗轮齿面上的离散点[4],但计算过程复杂。目前国内的蜗轮蜗杆都是在国外的齿轮测量中心进行检定,比如德国Klingelnberg及WENZEL的三坐标测量机。Klingelnberg公司齿轮测量中心的技术水平处于领先地位,我国计量院的齿轮样板的检测结果也以Klingelnberg的检测结果为准。

本文以ZA蜗轮为例,推导其齿面数学模型及啮合方程式,并规划测量网格,从而求解出蜗轮齿面的理论坐标。

1　ZA蜗轮齿面数学模型

1.1ZA蜗杆齿面方程

ZA蜗杆是用具有直线刃的梯形刀具在车床上加工而成[5]。刀具前刀面安装在过蜗杆轴线的水平位置上,刀具左右两直线刀刃同时切削蜗杆齿槽的两侧面。根据蜗杆的加工原理,将车刀刃口直线方程进行坐标转换,可得蜗杆螺旋面方程式(1):

(1)

式中:α为蜗杆的轴向齿形角;u为车刀直线刃口参数;参变数θ表示母线从起始位置绕z轴转过的角度;p为螺旋参数。对于左旋螺旋面,只需把式中pθ前的正号改为负号即可,本文所用蜗杆为右旋蜗杆。

根据空间啮合理论,为求蜗轮齿面方程式,先要得到蜗杆齿面的法线n的表达式。nx1、ny1、nz1为法矢量在x1、y1、z1三个坐标轴上的分量,其大小分别为：

(2)

根据上式可求得蜗杆齿面的法线矢量在三个坐标轴上的分量如式(3)所示,其单位法矢如式(4)所示。

(3)

(4)

1.2蜗轮蜗杆啮合坐标系的建立

蜗轮蜗杆啮合选用三个坐标系,图1给出了各坐标系之间的相对运动关系,∑1[o1;x1,y1,z1]是和蜗杆相固连的动坐标系,蜗杆轴和z1轴重合;∑2[o2;x2,y2,z2]是和蜗轮相固连的动坐标系,蜗轮轴和z2轴重合;∑[o;x,y,z]为空间固定坐标系,z轴和z1轴重合;∑2’[o2’;x2’,y2’,z2’]是空间辅助固定坐标系,z2’轴与z2轴重合。

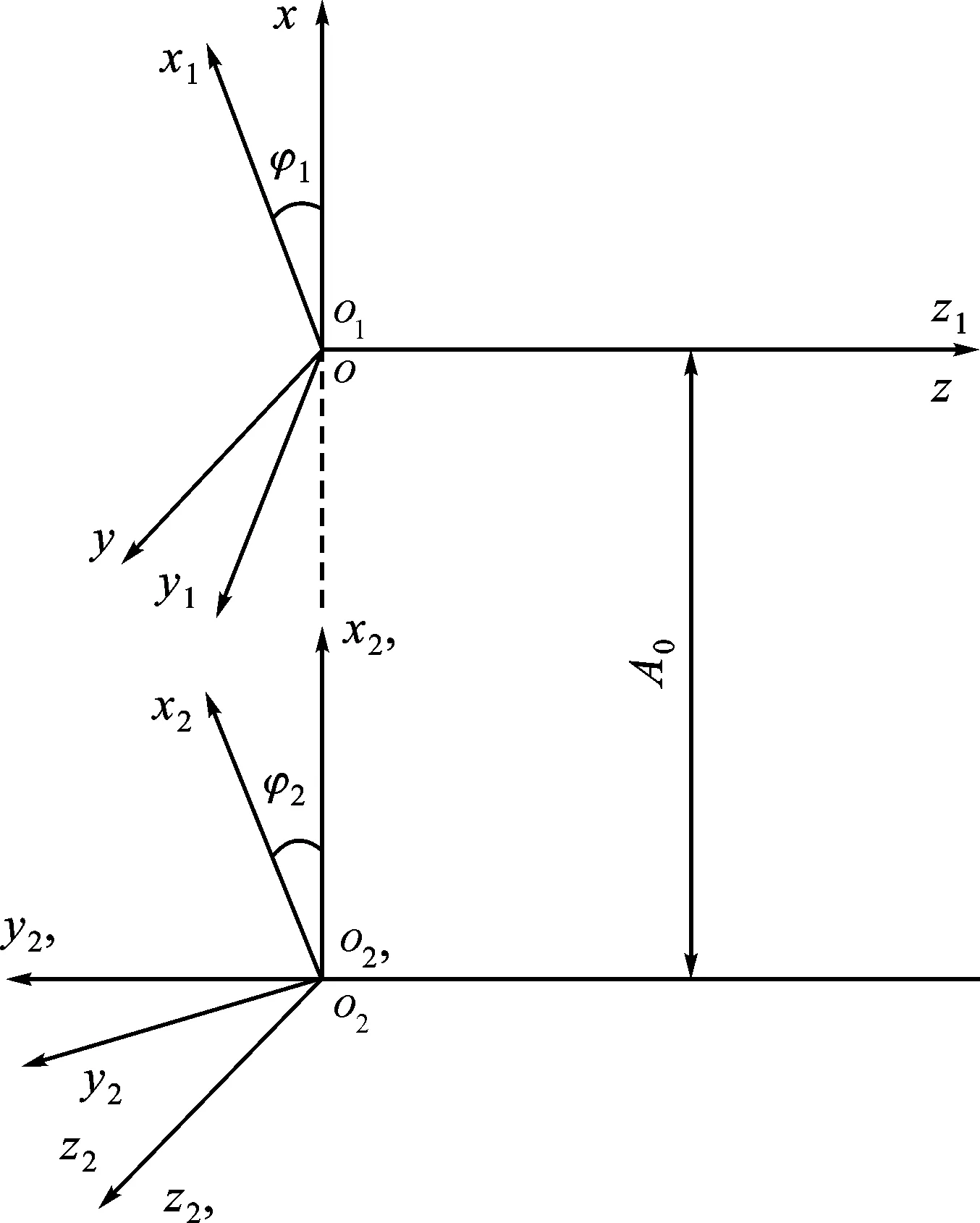
图1　蜗轮蜗杆啮合坐标系Fig.1　Meshing coordinate system of worm gear and worm

蜗轮和蜗杆的中心距为A0,φ1、φ2分别指啮合运动中蜗杆、蜗轮的转角。蜗杆与蜗轮连续啮合时,蜗杆绕z1轴转过φ1角时对应的蜗轮绕z2轴转过φ2角,φ1与φ2的关系满足传动比i12=φ1/φ2。

由∑1转换到∑2的转换矩阵见式(5)。

M21=

(5)

1.3ZA蜗轮蜗杆啮合方程

根据齿轮啮合原理,蜗轮蜗杆齿面在任意啮合瞬时呈线接触[5-6],在它们的切点处有公共的法平面和公共的法线n。两齿面在切点处的相对运动速度v12必然和法线垂直,这样才能保证两个齿面能够连续接触,既不会脱开也不会发生干涉。即蜗轮蜗杆啮合时应满足方程式(6)。

(6)

假设蜗杆与蜗轮啮合时,蜗杆以定角速度ω1绕z1轴旋转,蜗轮以定角速度ω2绕z2轴旋转,如图2所示。

图2　啮合点相对速度坐标Fig.2　Relative velocity coordinates of meshing point

当蜗杆转过φ1角时,对应蜗轮转过φ2,蜗杆齿面上的点p进入啮合,其相对速度v12为：

(7)

式中,ω12=ω1-ω2;r2=r1+τ; τ=A0i。

将式(4)和式(7)带入式(6)可推导出ZA蜗轮蜗杆啮合方程式(8):

pθsinα]-p2θtan(θ+φ1)=0

(8)

1.4ZA蜗轮齿面方程

蜗轮蜗杆齿面为一对共轭齿面,所以利用坐标变换将ZA蜗杆齿面上的接触线的坐标式变换到蜗轮坐标系中,即得到蜗杆的共轭齿面,也就是ZA蜗轮齿面的方程(见式(9))。

(9)

蜗轮蜗杆齿面为一对共轭齿面,所以在接触点处有公共的法线,把蜗杆齿面的法线方程经过坐标转换,可得到蜗轮齿面法矢(见式(10))。

(10)

2　蜗轮齿面网格划分

蜗轮的齿面是一种极为复杂的空间曲面,测量时只能选取齿面上的离散点进行检测。为了使得测量所取的离散点尽可能准确地描述蜗轮的齿面几何形状,同时又不产生测量数据冗余,就需要在蜗轮齿面的旋转投影面上进行网格规划。因为三坐标测量机的测头不能准确地测量齿面边界倒角以及齿根附近区域,所以在测量蜗轮的齿面时,需在齿面的四周预留一定的边界。

在设置网格测量参数时,主要有行和列两个参数:行数取4～15,列数取6～15。

在划分网格时,需要设置齿根处缩进量、齿顶处缩进量、角处缩进量及测量密度,以保证网格点在x2o2z2平面上均匀分布。在蜗轮齿面的旋转投影面上进行的网格规划如图3所示。由图3可知,网格的划分由两个参数决定,一个是角度参数β,一个是蜗杆半径参数r。β可根据蜗轮齿冠面角进行取值,r从蜗杆齿根到齿顶取值。可根据以下3个关系式求解齿面未知参数。

图3　网格划分示意图Fig.3　Schematic diagram of grid

首先，β、r及z2之间的几何关系满足式(11):

z2=rtanβ

(11)

其次,网格上的坐标点满足关系式(12):

(12)

式中,R为网格点在蜗轮上的半径,R=A0-rcosβ。

将式(9)中的z2用x2、y2表示,并将x2、y2、z2分别代入式(11)、(12),并与式(8)联立,可求解出蜗轮齿面方程的未知参数u、θ、φ1,然后φ2=φ1/i12。

将这四个参数带入蜗轮的齿面方程,便可求得网格划分坐标点处的坐标值。求解流程如图4所示。

图4　齿面网格坐标求解流程图Fig.4　Flow chart of grid coordinate for tooth surface

3　蜗轮理论齿面计算及测量结果

3.1阿基米德蜗轮齿面网格坐标计算

了解了蜗轮齿面网格点坐标理论值的求解方法,可通过MATLAB建立齿面方程组进行求解,划分网格为“5×9”,共45个网格点,输入的蜗轮蜗杆基本参数如表1所示。运行程序后部分网格点理论坐标值及单位法矢计算结果列于表2。

表1　ZA蜗轮蜗杆基本参数

表2　ZA蜗轮网格点理论及实测坐标值偏差及单位法矢计算结果

注:小括号内数据为该网格点的实测值。

3.2实测数据

蜗轮齿面网格点的理论坐标值和单位法矢求得之后,要完成蜗轮齿面的误差测量,需测出真实蜗轮齿面上的空间三维坐标值。本文选用三坐标测量机对蜗轮进行测量,由计算机程序提供求得的测点法矢,传到测量机,测量机将数据转换成运动,驱动测头测量。测头到位后读出实际测点的坐标,返回到计算机。ZA蜗轮上述相应点由三坐标测量仪测量的结果见表2中小括号中的数据。

由表2可知,x方向最大偏差为0.020 6 mm,在网格点(1,8)处;y方向最大偏差为0.035 9 mm,在网格点(1,1)处;z方向最大偏差为-0.012 7 mm,在网格点(1,1)处。在x、y、z方向上出现最大偏差的网格点均位于划分网格的边界,这是由于在蜗轮的测量过程中,触测蜗轮齿面边界,有可能会产生测量系统误差。由误差大小可知,本文对ZA蜗轮齿面数学模型的建立及求解方法是正确的。

4　结　语

本文基于ZA蜗轮齿面方程及啮合方程,对蜗轮进行了网格点的规划。通过MATLAB编程,根据被测蜗轮的结构参数,求解出蜗轮齿面网格点的理论坐标值与单位法矢,并在三坐标测量机上对ZA蜗轮进行检测,检测结果证明了数学模型的建立以及网格坐标点的求解方法是可行且有效的。

[1] 石照耀, 费业泰, 谢华锟. 齿轮测量技术100年——回顾与展望[J]. 中国工程科学,2003,5(9):13-17.

SHI Zhaoyao, FEI Yetai, XIE Huakun. 100 Years of gear measurement technology—Review & Prospect[J]. Engineering Science,2003,5(9):13-17.

[2] 王树人, 刘平娟. 圆柱蜗杆传动啮合原理[M]. 天津: 天津科学技术出版社, 1982.

[3] LITVIN F L. Gear geometry and applied theory[M]. Englewood Cliffs, NJ: Prentice Hall, 1994.

[4] 李立新, 曹谊勃. 基于双三次B样条曲面的ZA蜗轮实体建模方法[J]. 工程设计学报,2009,16(4):286-291.

LI Lixin, CAO Yibo. Solid modeling method of ZA worm-gear based on bicubic B-spline surface[J]. Journal of Engineering Design,2009,16(4):286-291.

[5] 吴序堂. 齿轮啮合原理[M]. 西安: 西安交通大学出版社,2009:154-156.

[6] 傅则绍. 微分几何与齿轮啮合原理[M]. 东营:石油大学出版社,1999.

(责任编辑王卫勋，王绪迪)

Modeling and calculation of Archimedes worm gear tooth surface

SONG Dan,LIU Jun,YAN Kejun

(School of Mechanical and Precision Instrument Engineering, Xi’an University of Technology, Xi’an 710048, China)

In this paper, based on the method for processing the Archimedes worm and worm gear (ZA), and the transformation of the space meshing coordinates of the worm and worm gear, the mathematical model of the tooth surface of ZA worm gear and the meshing equation is derived. Then the mesh of the tooth surface is carried out in the direction of worm gear axis, with the nonlinear equations established according to the meshing principle of the worm and worm gear and the numerical relationship of the mesh nodes. Finally, the coordinate value and the normal vector of the ZA worm gear grid points are obtained by MATLAB, with the feasibility of the algorithm verified on the three coordinate measuring machine.

ZA worm gear; mathematical model of tooth surface; meshing; three coordinate measuring machine

10.19322/j.cnki.issn.1006-4710.2016.03.021

2016-01-13

西安市科技计划资助项目(CXY1441(5))

宋丹,女,硕士生,研究方向为测试计量技术。E-mail:812530570@qq.com

刘君,女,教授,研究方向为光电测试技术与计算机测控。E-mail:junliu87@xaut.edu.cn

TH132.44

A

1006-4710(2016)03-0370-04