基于分段线性混沌网络的序列密码算法
林 敏 龙 飞
(贵州大学大数据与信息工程学院 贵州 贵阳 550025)
基于分段线性混沌网络的序列密码算法
林敏龙飞
(贵州大学大数据与信息工程学院贵州 贵阳 550025)
针对Logistic混沌序列容易被重构的问题,引入一种外部密钥对Logistic方程的初始值和参数进行加密;然后给出一种分段线性混沌网络模型。利用Logistic序列对初值的敏感性对混沌网络进行敏感和扩散处理,通过更新控制参数使混沌网络迭代运算产生随机性良好的序列密码。最后的算法分析和仿真实验表明,该算法的密钥具有良好的敏感性,生成的随机序列具有良好的随机性,满足密码学要求。
混沌序列外部密钥分段线性混沌网络序列密码
0 引 言
信息安全一直是与我们生活息息相关的重要问题,而保护信息安全最常用的手段就是数据加密了。自K.Aihara等人提出混沌神经网络模型以来,混沌与神经网络相结合应用于数据加密就得到了不断发展。目前主要的研究方法有:(1) 采用已知的混沌序列来训练神经网络模型,使得神经网络能够近似生成相同的混沌序列,然后将已知的混沌序列作为公钥,训练好的神经网络权重和阈值参数作为私钥,实现数据加密。(2) 利用离散Hopfield网络的混沌吸引性和初始状态与吸引子的单向映射性,可以将离散Hopfield网络的稳定吸引子作为密钥实现加密。文献[1]将神经网络互学习模型与混沌系统融合互扰,提出了一种新型复合流密码。文献[2]把Diffe-Hellman密钥交换协议和流密码算法相结合,设计了一种基于神经网络混沌吸引子的混合加密算法。文献[3]将Hermite正交多项式引入到神经网络激励层,实现了“一次一密”异步加密算法。文献[4]利用Hopfield网络的混沌吸引性与线性反馈移位寄存器相结合,提出了一种流密码加密方案。将混沌与神经网络相结合应用于数据加密最主要的就是利用混沌序列的混沌特性了,但是文献[5]也指出了混沌序列在数据加密中存在序列被重构缺陷,而且文献[6]对Logistic方程的四点和十六点序列片段完全实现了重构。因此,简单的混沌序列加密方法是存在被破解的风险的。针对这个问题,本文引入一种外部密钥对Logistic方程进行加密,同时提出一种分段线性混沌神经网络模型,通过一种敏感和扩散处理,使得混沌网络模型也具有良好的敏感性,生成良好的随机序列。
1 Logistic映射
Logistic映射是经典的混沌序列映射,由于其实现方法简单,容易被窃密者利用相空间进行重构,从而构造出混沌方程的形式[7]。因此,本文为了增强Logistic映射的保密性,引入一个外部密钥对Logistic映射的初始值和参数进行加密。
采用24位的二进制数字K1作为一个外部密钥来初始化Logistic映射的初始值和参数。设K1的16进制表示为K1=k1k2k3k4k5k6,″k1k2k3k4k5k6″为外部密钥。其中″k1k2k3″用于生成Logistic映射的输入控制参数r,″k4k5k6″用于生成Logistic映射的初始值X0。
在本文中,使用的Logistic映射如下:
Xn+1=r×Xn(1-Xn)Xn∈(0,1)
其中:r为输入控制参数,X0为Logistic映射的初始值。它们由外部密钥经过运算产生,运算过程中″k1k2k3k4k5k6″分别转化为相应的十进制数进行运算。因此:
2 混沌神经网络模型
本文采用的混沌神经网络结构如图1所示,网络的输入层对数据进行预处理,每一层的传输函数由函数f(·)和g(·)组合构成,实现对输入的数据进行混沌处理。

图1 混沌神经网络结构图
设二进制密钥K2长度为16 bit,将其按行二维化分组,每一行为一组,形成4×4的二进制数据矩阵D1:
每一行数据为一组,共有4组,分别为D11、D12、D13、D14。在本文中,为了提高密钥K2的敏感性,分别对D11、D12、D13、D14作如下处理:
设D11、D12、D13、D14的十进制表示分别为h1、h2、h3、h4,则:
其中:X为Logistic方程生成的值,n0为区间[50,100]上的整数。
将变换后的数据输入到混沌神经网络,则:
其中α为函数g(·)的参数。
函数g(x)将区间(-∞,∞)上的数映射到区间(0,1)上。混沌网络的传输函数f(·)为一个分段线性混沌映射函数,其输入值要求在区间(0,1)上,这与函数g(·)的映射区间刚好吻合。n1表示函数f(·)的迭代次数,Q1为函数f(·)的控制参数矩阵,传输函数f(·)的数学模型描述如下:
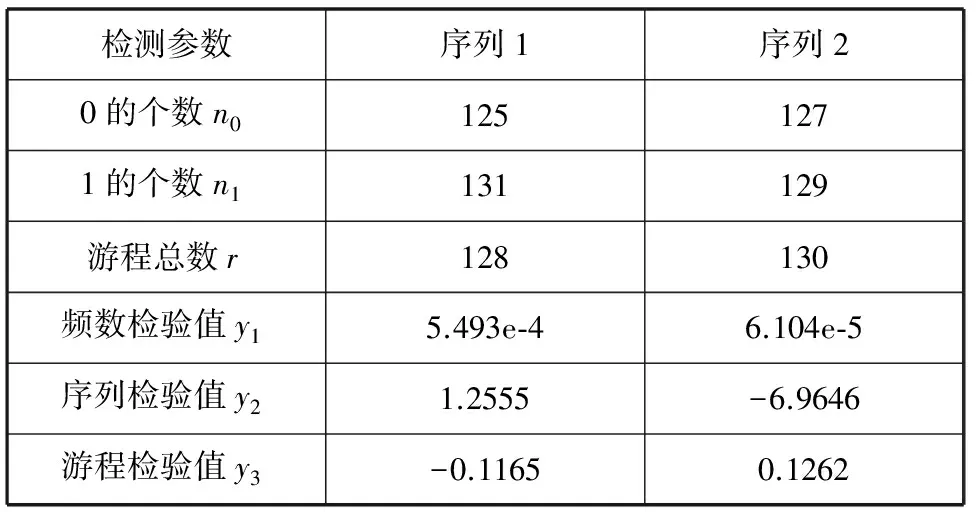
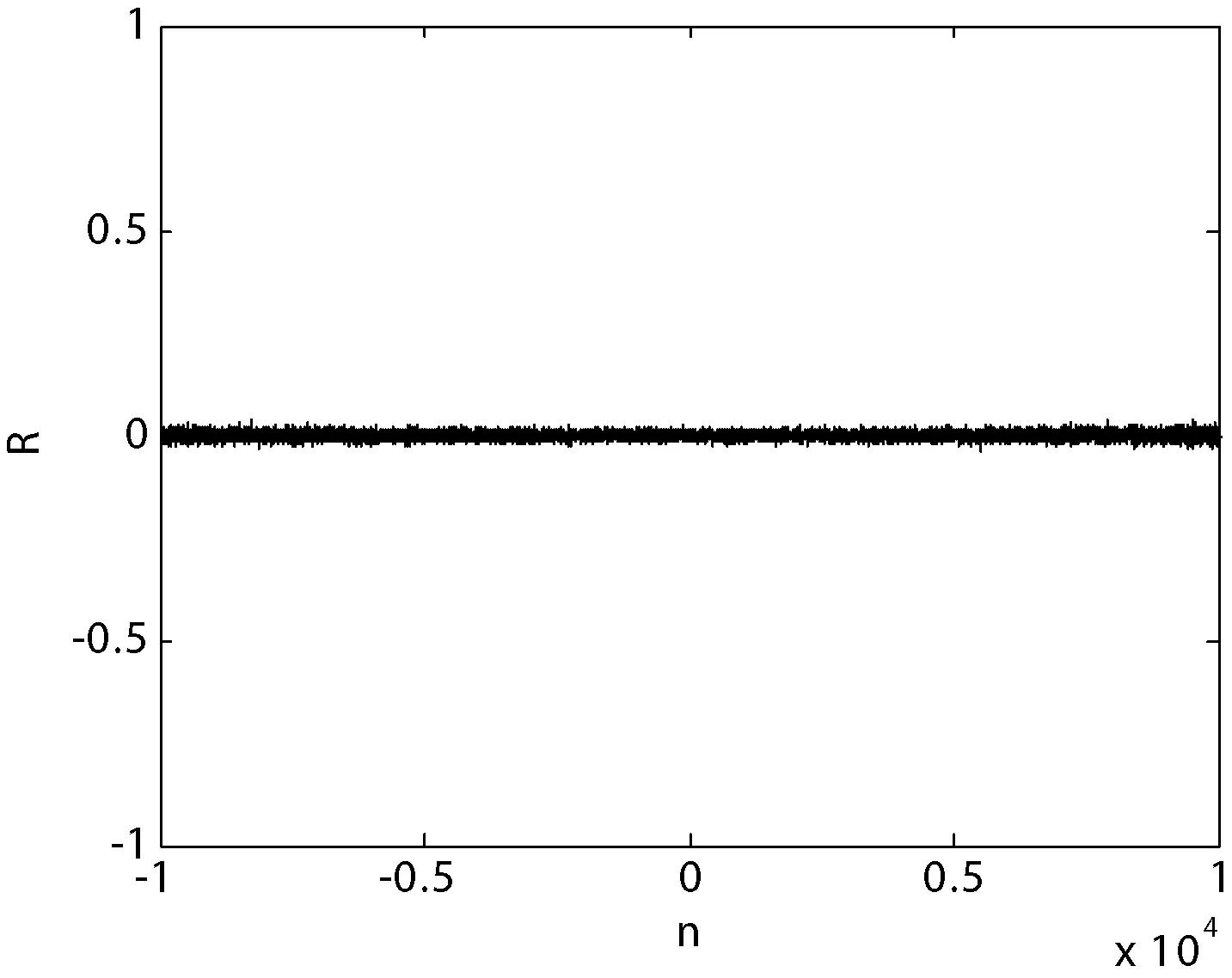
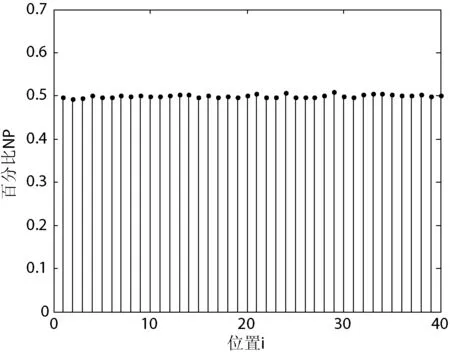
其中:x(k)是混沌映射的状态,q是控制参数,并且0 D3=fn2(g(W2D2+B2),Q2) 其中,D2是网络第二层的输入,W2和B2分别是第二层神经元的权值和阈值;n2表示函数f(·)的迭代次数,Q2为函数f(·)的控制参数。 由于网络的每一个神经元输出值都在区间(0,1)上,因此可以采用如下方法来更新控制参数Q1、Q2的值,通过网络运算得到不同的随机值D3。 Q1=(0.2×D2)+0.4 Q2=(0.2×D3)+0.4 每运行一次混沌网络,都会生成一个随机值D3,并更新Q1和Q2的值。利用更新后的Q1和Q2重复运行混沌网络就可以得到由随机值D3组成的随机序列。 为了将混沌网络生成的随机序列应用于数据加密,本文引入转换函数T(x),使生成的随机序列转换为0-1随机序列,T(x)定义如下: 由于网络生成的随机值在区间(0,1)上,因此本文将区间(0,1)分成N等份,N值越大,(0,1)区间划分越精细,数据精度越高。 (1) 输入密钥K1来初始化Logistic映射,并迭代运算Logistic映射200次,设X=[x101x102x103…x199x200]用于存储后面100次的混沌值。 (2) 利用X来初始化扩散矩阵W和混沌网络的权值与阈值。W是4×4的矩阵,W1是2×4的矩阵,B1是2×1的矩阵,W2是1×2的矩阵,B2是1×1的矩阵,从X中提取元素来分别初始化W、W1、B1、W2、B2。 (5) 通过量化函数T(x)将生成的随机序列转换成相应的二进制随机序列。 本文通过理论分析和实验仿真的方法来对算法的密钥空间大小、0/1的个数统计、随机序列的相关性和密钥的敏感性进行分析,并得出相应结论。仿真实验数据如下: K1=[1,1,1,0;1,0,1,0;0,0,1,1;1,1,0,0;0,1,1,1;0,1,1,1] K2=[0,0,0,1;0,0,1,0;0,1,1,0;1,0,0,0] n0=60,n1=4,n2=5,α=2,N=64,Q1=[0.5,0.5]T,Q2=0.5。 5.1密钥空间分析 本文的加密密钥由K1和K2组成,密钥空间由K1和K2的长度决定。设它们的长度分别为L1和L2,则密钥空间为2(L1+L2)。L1+L2越大,密钥空间越大。在本文中L1=24、L2=16,密钥空间大小为240。显然,L2的长度大小是可变的,增加L2的长度可以增加密钥空间大小。但是,增加密钥L2的长度时,混沌网络的输入个数也会增多,相应的混沌网络层数也会增多,网络迭代运行一次的时间开销将会增大。当生成的随机序列长度非常大时,整个网络运行的时间开销将会是非常大的。 5.2统计分析 一个有效的二进制随机序列必须满足0/1比例近似相等[9]。因此,本检验的目的是确定序列中0/1的比例是否与真正的随机序列中的0/1的比例近似相等。同时,本文参考文献[12]的方法对生成的随机序列进行频数检验、序列检验和游程检验。 为此,随机选取两个长度为256的随机序列进行统计分析,分析结果如表1所示。 表1 统计分析结果 由表1可以看出,序列1和序列2中“0”与“1”的个数接近相等,满足随机序列要求。同时,频数检验值y1均小于3.84,能通过频数检验;序列检验值y2均小于5.99,能通过序列检验;游程检验值y3远小于1.96,能通过游程检验。因此,生成的随机序列具有很好的随机性。 为了进一步验证生成序列的随机性,本文将上述随机选取的两组随机序列与文献[11,12]中的统计分析结果进行比较。文献[11,12]的统计分析结果如表2所示。 表2 文献[11,12] 统计分析结果 由表1和表2可以看出,本文生成的随机序列中“0”与“1”的相差个数要比文献[12]中“0”与“1”的相差个数更小。因此,本文生成的0/1序列随机性更好。同时,本文的频数检验值y1、序列检验值y2和游程检验值y3均小于文献[12]中对应的值。因此,本文生成的0/1序列能够更好地通过频数检验、序列检验和游程检验。与文献[11]相比,本文生成的随机序列中“0”与“1”的相差个数接近文献[11]中“0”与“1”的相差个数。同时,本文的频数检验值y1和游程检验值y3在有些情况下小于文献[11]中对应的值,说明本文生成的0/1序列在有些情况下能够更好地通过频数检验和游程检验。但是,本文的序列检验值y2均大于文献[11]中对应的值,说明文献[11]中生成的0/1序列能够更好地通过序列检验。总体上来说,本文算法在频数检验、序列检验和游程检验中优于文献[12],在有些情况下优于文献[11]。 5.3相关性分析 序列的自相关函数变化越小,说明序列的随机性越好。序列的互相关函数越接近零,说明两个序列越互不相关[10]。图2是初始密钥为K1和K2时生成的0/1序列的自相关函数图。图3是密钥K1或K2随机改变一位时生成的0/1序列对比图,实线代表原序列,虚线代表新序列。图4是两个序列的互相关函数图。 图2 生成0-1序列的自相关函数图 图3 密钥改变一位时生成的0/1序列对比图 图4 序列的互相关函数图 由图2可以看出,自相关函数变化很小,生成的序列随机性良好。由图3可以看出,只要改变密钥K1或K2中的一位,生成的0/1序列将会有很大的不同;由图4可以看出,改变密钥K1或K2中的一位时,生成的新序列与原序列的互相关函数值接近0,说明两个序列互不相关。 5.4密钥敏感性分析 Logistic映射生成的混沌序列对初始值具有良好的敏感性,由于密钥K1用于生成Logistic方程的初始值,因此K1也具有良好的敏感性。同时,本文利用Logistic映射对密钥K2进行了敏感和扩散处理,使得K2也具有良好的敏感性。为了验证密钥K1和K2的敏感性,分别改变密钥K1、K2中的一位,并统计新随机序列与原随机序列的不同位数所占的百分比。设i表示K1和K2中每一位对应的位置编号,则1≤i≤Lg,Lg为密钥K1和K2的长度总和。在本文中,Lg=40。NP表示新随机序列与原随机序列的不同位数占序列总数的百分比,NP的计算公式为: 其中,D(n)和D′(n)分别表示原随机序列和新随机序列,NK表示序列D(n)的总位数,NP(i)表示改变第i位时所对应的百分比。 根据分组密码测度中的严格雪崩准则,改变密钥中的任一比特,应导致密文中大约50%比特的变化。图5是对密钥长度Lg=40,生成序列长度NK=20 000时得到的百分比统计结果。 图5 密钥改变一位时生成的序列所改变的百分比 由图5可以看出,密钥改变一位时生成的序列所改变的百分比均接近50%,满足严格雪崩准则。因此,密钥K1和K2均具有敏感性。 综上所述,本文算法生成的0/1序列具有良好的随机性,密钥具有很强的敏感性。此外,本文采用24位的外部密钥来生成混沌初值和控制参数,与文献[13]直接采用混沌初值和控制参数作为密钥相比,本文的密钥更方便管理。同时,解决了文献[6]提出的Logistic序列易被重构的问题,使得密钥的安全性更好。 将混沌与神经网络相结合,引入外部密钥,提出一种新的生成随机序列的方法,以较少位数的密钥生成无限长度的随机序列。同时,对密钥进行敏感和扩散处理,增强了密钥的敏感性,并从仿真实验结果中得到了验证。但是,文中的密钥空间大小为240,以目前计算机的运算速度,存在被暴力破解的风险。因此,进一步的研究方向将会考虑增加密钥空间大小,同时考虑到算法的时间开销,提高运算效率。 [1] 陈铁明,蒋融融.混沌映射和神经网络互扰的新型复合流密码[J].物理学报,2013,62(4):040301. [2] 何峥,李国刚.基于神经网络混沌吸引子的混合加密[J].通信技术,2012,45(5):50-52. [3] 邹阿金,张雨浓,肖秀春.Hermite混沌神经网络异步加密算法[J].智能系统学报,2009,4(5):458-462. [4] 赵全习,胡文志,郑连清.一种流加密方案的设计与分析[J].计算机应用研究,2007,24(12):191-192,234. [5] 孙百瑜,高俊山,吴宏伟.基于置换乱序的混沌加密算法[J].自动化技术与应用,2005,24(2):7-9. [6] 高俊山,孙百瑜,韩伟.基于混沌理论的控制轨道函数构造[J].电机与控制学报,2002,6(2):150-153,167. [7] Kengnou Telem,Adelade Nicole,Meli Segning,et al.A Simple and Robust Gray Image Encryption Scheme Using Chaotic Logistic Map and Artificial Neural Network[J].Advances in Multimedia,2014,2014:132-144. [8] Singla Prateek,Sachdeva Payal,Ahmad Musheer.A Chaotic Neural Network Based Cryptographic Pseudo-Random Sequence Design[C]//Proceedings-4th International Conference on Advanced Computing and Communication Technologies,2014:301-306. [9] 任志山.基于混沌神经网络混沌二进制序列的性能分析及实现[C]//中国电子学会信息论分会.中国电子学会第十五届信息论学术年会暨第一届全国网络编码学术年会论文集(上册),2008,6. [10] 蔺小梅,李国刚,张泽普.采用OHNN和M-LFSR的字序列密码加密方案[J].华侨大学学报:自然科学版,2014,35(5):519-522. [11] 吴君钦,陈天栋,李康顺.一种基于多目标差分演化的序列密码算法[J].计算机应用研究,2014,31(7):2139-2143. [12] 胡能发,邓永发.基于遗传算法的序列密码生成方法[J].计算机工程与设计,2005,26(8):2190-2192. [13] 邹于丰.基于Legendre多项式混沌神经网络的异步保密通信[J].计算机应用与软件,2012,29(12):315-317. STREAM CIPHER ALGORITHM BASED ON PIECEWISE LINEAR CHAOTIC NETWORKS Lin MinLong Fei (College of Big Data and Information Engineering,Guizhou University,Guiyang 550025,Guizhou,China) In response to the issue that Logistic chaotic sequences are easily to be reconstructed, we introduced an external key to encrypt initial values and parameters of Logistic equation; and then put forward a piecewise linear chaotic networks model. It uses the sensitivity of Logistic sequence on initial values to process the chaotic networks in terms of sensitivity and diffusion, and enables the chaotic networks to iteratively operate through renewing the control parameters so as to generate the stream cipher with good stochastic property. The final algorithm analysis and simulation experiments proved that the keys of the algorithm have good sensitivity; and the generated random sequences have good stochastic property as well, and satisfy the requirement of cryptography. Chaotic sequencesExternal keyPiecewise linear chaotic networksStream cipher 2015-05-20。国家自然科学基金项目(61263005)。林敏,硕士生,主研领域:神经网络,数据加密。龙飞,教授。 TP309.7 A 10.3969/j.issn.1000-386x.2016.09.0713 量化处理

4 生成0-1随机序列
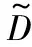
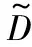
5 算法分析



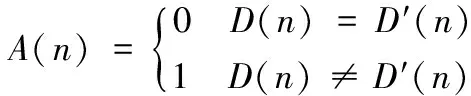
6 结 语

