基于蝙蝠算法的贝叶斯分类器优化研究
蒋礼青 张明新 郑金龙 戴 娇
1(中国矿业大学计算机科学与技术学院 江苏 徐州 221116)2(常熟理工学院计算机科学与工程学院 江苏 常熟 215500)
基于蝙蝠算法的贝叶斯分类器优化研究
蒋礼青1,2张明新2*郑金龙2戴娇1
1(中国矿业大学计算机科学与技术学院江苏 徐州 221116)2(常熟理工学院计算机科学与工程学院江苏 常熟 215500)
朴素贝叶斯分类器是一种应用广泛且简单有效的分类算法,但其条件独立性的“朴素贝叶斯假设”与现实存在差异,这种假设限制朴素贝叶斯分类器分类的准确率。为削弱这种假设,利用改进的蝙蝠算法优化朴素贝叶斯分类器。改进的蝙蝠算法引入禁忌搜索机制和随机扰动算子,避免其陷入局部最优解,加快收敛速度。改进的蝙蝠算法自动搜索每个属性的权值,通过给每个属性赋予不同的权值,在计算代价不大幅提高的情况下削弱了类独立性假设且增强了朴素贝叶斯分类器的准确率。实验结果表明,该算法与传统的朴素贝叶斯和文献[6]的新加权贝叶斯分类算法相比, 其分类效果更加精准。
分类朴素贝叶斯属性加权蝙蝠算法
0 引 言
朴素贝叶斯分类器NBC(Naive Bayes Classifiers),训练简单,具有很强的健壮性和高效性;通过比较发现,朴素贝叶斯分类法可以与经过挑选的神经网络及决策树相媲美[1],已经成功地应用到分类、聚类及模型选择等数据挖掘任务之中[2,3]。由于朴素贝叶斯分类器存在条件独立性假设,使其在预处理数据集时要进行属性约简。然而在实际应用中,大多数据集不满足条件独立性假设,针对朴素贝叶斯分类器的不足,学者学习研究贝叶斯信念网络来改进其分类性能,文献[4]证明,学习训练数据集并得到一个最优贝叶斯网络是NP-hard问题。在文献[5]中,Zhang H提出根据属性影响力的不同,给相应属性赋予权值,这种方法模型称为加权朴素贝叶斯模型;张步良提出基于分类概率加权的朴素贝叶斯分类方法[6]。他们提出的属性加权方法具有局限性,如张步良的方法是通过对每个属性做朴素贝叶斯分类,得到正确分类该属性的概率,把该概率作为权值,而不考虑某个属性对整体数据分类准确度的影响。针对传统加权朴素贝叶斯分类器的缺点,本文利用蝙蝠算法进行全局最优属性权值的搜索,目标是寻找影响整体数据分类精准度最强的权值,从而优化文献[6]属性加权方法。
蝙蝠算法BA(Bat Algorithm),是2010年由Yang X S教授提出的一种新的启发式群智能算法[7]。已有许多学者对蝙蝠算进行研究,与粒子群算法、遗传算法及和声算法等相比,蝙蝠算法有更好的计算精度和计算效率[8,9]。目前,蝙蝠算法已经广泛应用于自然科学与工程科学领域中[10]。针对原始蝙蝠算法存在寻优不精、收敛慢和早熟的缺点,本文用新的改进方法对其进行改进,称为改进的蝙蝠算法IBA(Improved Bat Algorithm)。
本文提出利用改进的蝙蝠算法优化朴素贝叶斯分类器NB-IBA的算法,将蝙蝠算法与朴素贝叶斯分类算法结合,采用IBA来自动搜索每个属性权值,削弱条件独立性假设,优化朴素贝叶斯分类器。试验表明,NB-IBA算法确实能提高朴素贝叶斯分类器分类的精准度。
1 加权朴素贝叶斯分类算法
1.1朴素贝叶斯模型[1]
设D是训练元组与类标号集合。每个元组用一个n维向量表示属性向量,如X={x1,x2,…,xn},描述由n个属性A1,A2,…,An对元组的n个测量。假设类个数为m个,为C1,C2,…,Cm。给定一个X训练元组,分类器预测属于类Ci的X,当且仅当:
P(Ci|X)>P(Cj|X)1≤j≤mj≠i
(1)
当p(Ci|X)最大化,称此时的类Ci为“最大后验假设”。
类先验概率可以用p(Ci)=|Ci,D|/|D| 估计,其中|Ci,D|是D中Ci类的训练元组数。给定元组的类标号,因此:
=P(x1|Ci)P(x2|Ci)…P(xn|Ci)
(2)
可以根据X进行概率p(x1|Ci),p(x2|Ci),…,p(xn|Ci)的估计。考虑属性值是离散的还是连续的:
第一,如果Ak是离散值,则p(xk|Ci)为属性Ak中值为xk的且属于Ci类的元组数除以Ci类的元组数|Ci,D|,Ak,Ci都属于D。
第二,如果Ak是连续值属性,假定连续值属性服从高斯分布,由下式定义:
(3)
因此:
P(xk|Ci)=g(xk,μCi,σCi)
(4)
函数g中第二和第三个参数分别是Ci类训练元组属性Ak的均值(即平均值)和标准差。
后验概率公式为:
(5)
测试样(E={X1,X2,…,Xn}) 被分在后验概率最大的类中,因为p(X)为常数,计算则不作考虑,朴素贝叶斯分类器的模型为:
(6)
1.2加权朴素贝叶斯模型
首先在朴素贝叶斯分类器中用属性加权思想的是Webb等人[11]。本文运用加权算法直接用于每个条件概率p(xk|Ci)上,这样,可以用更加直接的方式影响分类的整个过程。加权朴素贝叶斯模型为:
(7)
其中,属性Ak的权值是wk,权值与属性影响力成正比关系,权值大,对应属性对分类正确率的影响力就强,反之则弱。
加权朴素贝叶斯的核心问题在于如何进行每个属性权值的计算。针对该问题,本文提出了一个计算权值的新方法,用改进后的蝙蝠算法进行各个属性权值的计算。
2 蝙蝠算法的改进及属性权值的计算
2.1蝙蝠算法
本文用蝙蝠算法优化朴素贝叶斯分类算法,蝙蝠算法是2010年由Yang Xinshe 教授提出[8]。在一个D 维搜索空间中,由n只蝙蝠组成的一个群体在飞行的过程中位置xi、速度vi、响度Ai和脉冲速率ri的初始化是由具体解决的问题确定。
群体数n的选择应综合考虑算法的可靠性和计算时间,对通常问题10只蝙蝠已足够,对于较复杂的问题可取50只。按照本文数据集的复杂性,蝙蝠个数取值公式如下[7]:
n=b+ξ×[c,d]
(8)
针对本文数据,b=c=10,d=40,ξ为属于[0,1]随机数。
飞行过程中蝙蝠更新位置xi、速度vi、响度Ai和脉冲速率ri的数学表达式为[12,13]:
fi=fmin+(fmax-fmin)β
(9)
(10)
(11)
当进入局部搜索,首先从最优解中任选个解,进行位置信息的随机变更,让每只蝙蝠基于局部解产生一个新解。公式如:
xnew=xold+εAt
(12)
其中,ε为一个随机数且属于[-1,1];At是同一个时间段总蝙蝠响度的平均值。
随着迭代过程的进行,更新脉冲发射响度Ai和速率ri。更新公式为:
(13)
其中,a和γ是常量。对于任意0
(14)
通常情况令a=γ,参数值的选择需要根据具体的试验要求。
2.2蝙蝠算法的改进
针对加权朴素贝叶斯分类器分类错误率与属性子集选择的计算,重新定义蝙蝠算法的目标函数为:
(15)
式中,Eval(xi)对应分类的错误率,TF是属性总数,SE是被选择参与分类的属性总数,δ和η分别表示分类精度的权重和特征子集比例的权重,其中δ∈[0,1]且η=1-δ。通常,分类的错误率比属性子集比例赋予更高的权重,本文设置δ=0.9,η=0.1。
针对蝙蝠算法易于陷入局部最优和对高维空间搜索精度不高的缺点,提出了建立禁忌搜索TS(taboo search)机制,使蝙蝠群算法具备跳出局部最优的能力。为避免进行迂回搜索,禁忌搜索机制拥有一个存储结构和禁忌准则,进而通过特赦准则来赦免禁忌表中的良好状态,保证探索的多样化,实现全局最优化;遇到没被特赦的蝙蝠个体,利用下文的随机扰动算子对其位置进行随机扰动,进一步减小匹配误差。
构造一个长度与蝙蝠个数相等的向量(禁忌表)记录蝙蝠群体迭代E次不变的局部最优位置信息,其可能为局部最优解,为了快速跳出局部最优,增加种群多样性,直接初始化蝙蝠群体。E值根据实际应用而定。在后续的搜索中,对存在禁忌表中的位置信息进行计数,然后以禁忌表中位置计数分量作为自变量构造罚函数[14]:
(16)
(17)
式中,ti是禁忌表的第i个分量,Δ是非常小的正数,a1>1,k是迭代次数。使用该罚函数根据式(14)重新构造相应的适应度函数,使适应度函数fitness(xi)与罚函数p(xi)近似成正比,则对应的适应度函数为:
(18)
如果某个位置被选作全局极值的次数越多,禁忌表记录次数分量的值越大,相应罚函数的值较大,对应的适应度函数值也较大,该位置被再次作为全局极值的可能性就较小,这样既可以剔除禁忌表中误判的局部最优解,又保证了种群的多样性;蝙蝠算法能最大可能跳离局部极值,得到精度更高的结果。若惩罚以后的适应度值仍最优,那么就用特赦准则,选取该位置为全局极值。
在对最优位置取值时与最佳位置会稍有偏差,所以在迭代过程中,如果遇到的位置在禁忌表中且通过罚函数计算的适应度值大于全局最优解的适应度值,那么这个局部最优解周围可能存在我们要找的全局最优解。所以对局部最优解位置的速度值加入一个随机扰动值,称为“随机扰乱算子”:
(19)
其中,φ为[0,1],|Ri|为第i个位置的取值范围大小,文中|Ri|=1。减少蝙蝠算法在局部最优解花费的时间,并进一步增强对局部最优解周围区域搜索。
2.3属性权值的计算过程
NB-IBA算法主要利用蝙蝠算法确定属性权值,寻找权值是个训练过程[15]。计算p(xk|Ci)时为避免零概率,要进行拉普拉斯校准。令wk=xi,并对wk进行标准化处理,使权值之和为1,每个蝙蝠对训练样本数据集分类进行预测,由于是有监督分类,可以得到样本数据分类的错误率Eval(xi)。NB-IBA算法详细步骤如下:
Step1数据预处理;读取样本数据,分别计算每个属性的先验概率和后验概率;
Step2用式(8)随机初始化蝙蝠群体数n,飞行过程中的位置xi(每只蝙蝠的位置代表一种属性子集的组合),速度vi,响度Ai,脉冲速率ri,常量E等各个参数。全局最优解best初始化为随机一个最优xi,当前最优适应度值为fitnessbest;
Step3令wk=xi,并对wk进行标准化处理。每个个体对样本数据集分类进行预测,用式(15)计算每个位置xi分类的适应度函数fitness(xi)的值;
Step4利用式(9)到式(11)生成新解,且每个参数都有最大与最小数值限制;
Step5判断xi位置信息是否在禁忌表taboo中,存在,则次数分量值加1,执行Step8;不存在,则转至Step6;
Step6判断x*和适应度函数是否连续E代不变,是则执行Step7,否则转至Step10;
Step7将x*位置信息保存到禁忌表taboo中,转至Step2;
Step8利用式(16)-式(18)计算适应度值fitness(xi),如果fitness(xi)>fitnessbest转至Step9;否则fitnessbest=fitness(xi),找到x*=xi,转至Step4;
Step9执行式(19),随机扰动,用式(11)更新位置信息,利用式(14)生成fitnessnew,转至Step10;
Step10判断是否满足变异条件(rand>ri),如果满足,用式(12)更新解的位置xnew;否则转至Step11;
Step11若rand>Ai& fitness(xi) Step12对蝙蝠列队,找到当前最佳解x*; Step13比较新位置的适应度值和当前最优适应度值是否满足fitnessbest≤ fitnessnew,如果满足,则更新当前最优适应度值和最优位置,否则转到Step14; Step14如果迭代结束,转至Step15,否则转至Step4; Step15输出全局最优解,可利用求得的权值wk=xi,用式(6)进行高维数据的分类预测。 本文数据集来自UCI,依据不同规模,挑其中5种数据集,分别为:House-Votes,Credit-a,SPECTF-Heart,Lung和Mushroom。House-votes是广泛使用的二元分类文献数据集,这个数据集描述了每位美国众议院议员投票情况,两个类标号分别代表民主党人和共和党人;Credit也是一个二元分类数据集,关注的是信用卡的应用;SPECTF-Heart是一个包含76种属性的二元类数据集,已经被用于心脏疾病的诊断中,其中1和0类编号表示患者是否存在心脏疾病;Lung是肺癌的病理学类型数据集,目的是展示最佳鉴别平面功率的病理类型;Mushroom(M-room)也是一个二元类数据集,包括假设样本在伞状蘑菇和环柄菇家族里与鳃蘑菇23种类型相同的特性描述。 图1 Vote数据集分类错误行数的收敛曲线 图3 MushRoom数据集分类错误行数的收敛曲线 针对数据集数据量较大且数据类型复杂的情况,进行多次试验,在100次迭代内,改进的蝙蝠算法收敛速度明显比未改进的快,不易陷入局部最优解,并能及早收敛至全局最优值。如图1到图3,上面曲线为改进前的蝙蝠算法,下面为改进后算法,刚开始的收敛速度都非常快,属于随机现象,但图1的5~15次迭代、图2的10~20与60~70次迭代和图3的1~10次迭代过程中改进的算法效果明显,改进后的算法可能利用禁忌搜索机制跳出了算法认为的局部最优或利用随机扰动算子针对局部最优进行随机扰动。因为E=9,改进后的算法在到达全局最优以前,几乎不存在错误行数连续E次不变的情况,若存在E次不变,是由于下一次迭代所选蝙蝠位置信息的目标函数值恰好与上次相同。 经过多次测试,改进后的蝙蝠算法收敛速度和准确度都明显优于未改进的蝙蝠算法。 图4为针对所有数据集,NB-IBA算法(目标函数为错误率与属性子集比例之和)的收敛曲线: 图4 NB-IBA算法分类错误率的收敛曲线 图4中横坐标为迭代次数,纵坐标为分类的错误率值,利用改进后的蝙蝠算法优化朴素贝叶斯分类器,其分类的错误率明显下降,即分类的准确率明显提升。 本试验对朴素贝叶斯分类算法(NB)、文献[6]的新特征加权朴素贝叶斯分类算法(NB-W)以及NB-IBA算法进行试验对比,NB-IBA算法在试验的时候进行15次训练,把所得属性权值取均值,各算法的分类精度如表1所示。 表1 分类精度对比 本文利用五个UCI的数据集进行算法的验证,除了Vote数据集,其余数据集所选择的属性与总属性数值一样,此时目标函数中的TF=SE。在这些数据集试验中子属性集的选择对目标函数值不起作用,最终为计算错误率,也可以针对不同的属性选择进行试验。针对Vote数据集,TF=17,SE=16。 图5为表1的展现。 图5 3种算法对5个数据集分类错误率对比 图5中,横坐标1~5数字按顺序表示表1中5个数据集,纵坐标为分类的错误率。用本文提出的NB-IBA算法进行分类时,所有用到的数据集的错误率普遍比NB和NB-W低,若有数据集在测试数据上分类错误率偏高,可能是所设置的参数不适合、该训练样本设置的不合理或该数据集基本满足条件类独立性假设。 总的来说,NB-IBA在处理大部分数据集时能准确进行分类,到达理想的精确度。在算法的运行时间上,由于NB-IBA算法需要迭代地进行权值的搜索,因此训练分类器的时间会比NB和NB-W慢一点,待训练后,在以后的分类过程中,不仅速度与NB相当,精确率大幅度提高。本文在将位置转换为权值时对其进行标准化处理,并不是直接用蝙蝠的位置作为权值。蝙蝠算法的参数根据具体问题具体设置,调整参数,可达到更令人满意结果。 现有朴素贝叶斯分类算法条件独立性假设与现实存在差异,本文利用给每个属性赋予不同权值的方法削弱类独立性假设。为进一步提高朴素贝叶斯的分类精准度,本文提出利用改进的蝙蝠算法优化贝叶斯分类器,改进的蝙蝠算法自动搜索属性权值,并不是用蝙蝠位置作为权值,要对位置信息归一化处理。由于传统蝙蝠算法存在易陷入局部最优、早熟和收敛慢现象,本文改进蝙蝠算法,利用禁忌搜索机制避免算法陷入局部最优和早熟并达到全局最优化,利用随机扰动算子对局部最优解进一步搜索,找到真正的全局最优解,最终实现快速收敛。本文提出的NB-IBA 算法可以根据数据特征提高朴素贝叶斯分类器精准度,只需极少训练时间实现对朴素贝叶斯分类器的优化。试验表明,NB-IBA相比传统NB和文献[6]的新NB-W算法,提高分类的精准度并证明了算法的可行性和有效性。 [1] Jiawei Han,Micheline Kamber.数据挖掘概念与技术[M].范明,孟小峰,译.北京:机械工业出版社,2012:226-230. [2] 徐光美,刘宏哲.基于特征加权的多关系朴素贝叶斯分类模型[J].计算机科学,2014,41(10):283-285. [3] Chickering D M.Learning Bayesian Networks is NP-Complete[J].Lecture Notes in Statistics,1996,10(2):594-605. [4] Zhang H.Learning weighted naive Bayes with accurate ranking[C]//Data Mining,2004.ICDM '04.Fourth IEEE International Conference on.IEEE,2004:567-570. [5] Zhang H.Learning weighted naive Bayes with accurate ranking[C]//Data Mining,2004.ICDM '04.Fourth IEEE International Conference on.IEEE,2004:567-570. [6] 张步良.基于分类概率加权的朴素贝叶斯分类方法[J].重庆理工大学学报:自然科学版,2012,26(7):81-83. [7] Yang X S.A New Metaheuristic Bat-Inspired Algorithm[M].Nature Inspired Cooperative Strategies for Optimization (NICSO 2010).Springer Berlin Heidelberg,2010:65-74. [8] 李枝勇,马良,张惠珍.蝙蝠算法收敛性分析[J].数学的实践与认识,2013,43(12):182-189. [9] Yang X S,Gandomi A H.Bat algorithm:a novel approach for global engineering optimization[J].Engineering Computations,2012,29(5):464-483. [10] Yang X S.Bat Algorithm:Literature Review and Applications[J].International Journal of Bio Inspired Computation,2013,5(3):141-149. [11] Webb G I,Pazzani M J.Adjusted probability Naive Bayesian induction[J].Lecture Notes in Computer Science,1998,11(1):285-295. [12] Yilmaz S,Kucuksille E U,Cengiz Y.Modified Bat Algorithm[J].Elektronika Ir Elektrotechnika,2014,20(2):71-78. [13] 王文,王勇,王晓伟.一种具有记忆特征的改进蝙蝠算法[J].计算机应用与软件,2014,31(11):257-259,329. [14] 张世勇,熊忠阳.基于禁忌搜索的混合粒子群优化算法[J].计算机研究与发展,2007,44(S1):339-343. [15] 连阳阳,任淑霞.一种基于离散粒子群优化的贝叶斯分类算法[J].科技信息,2014(4):66-71. ON BAYESIAN CLASSIFIER OPTIMISATION BASED ON BAT ALGORITHM Jiang Liqing1,2Zhang Mingxin2*Zheng Jinlong2Dai Jiao1 1(School of Computer Science and Technology,China University of Mining and Technology,Xuzhou 221116,Jiangsu,China)2(SchoolofComputerScienceandEngineering,ChangshuInstituteofTechnology,Changshu215500,Jiangsu,China) Naive Bayesian classifier is a widely used simple and efficient classification algorithm, but there is a difference between the ″naive Bayesian hypothesis″ of conditional independence and the reality, such hypothesis restricts the accuracy of naive Bayesian classifier. To cripple this hypothesis, we used the improved bat algorithm (IBA) to optimise naive Bayesian classifier. IBA introduces Taboo search mechanism and random perturbation operator to prevent the naïve Bayesian classifier from falling into local optimal solution, and thus accelerates the convergence rate. IBA automatically searches the weight value of every attribute, by assigning different weight to each attribute, it weakens the hypothesis of independence and enhances the accuracy of naive Bayesian classifier without greatly increasing the cost of calculation. Test result showed that comparing with traditional naive Bayesian and newest weighted Bayesian classification algorithm proposed in paper[6], the proposed algorithm has higher accuracy in classification effect. ClassificationNaive BayesianAttribute weightingBat algorithm 2015-06-19。国家自然科学基金项目(61173130)。蒋礼青,硕士生,主研领域:数据挖掘。张明新,教授。郑金龙,硕士。戴娇,硕士生。 TP301.6 A 10.3969/j.issn.1000-386x.2016.09.0613 仿真实验
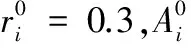
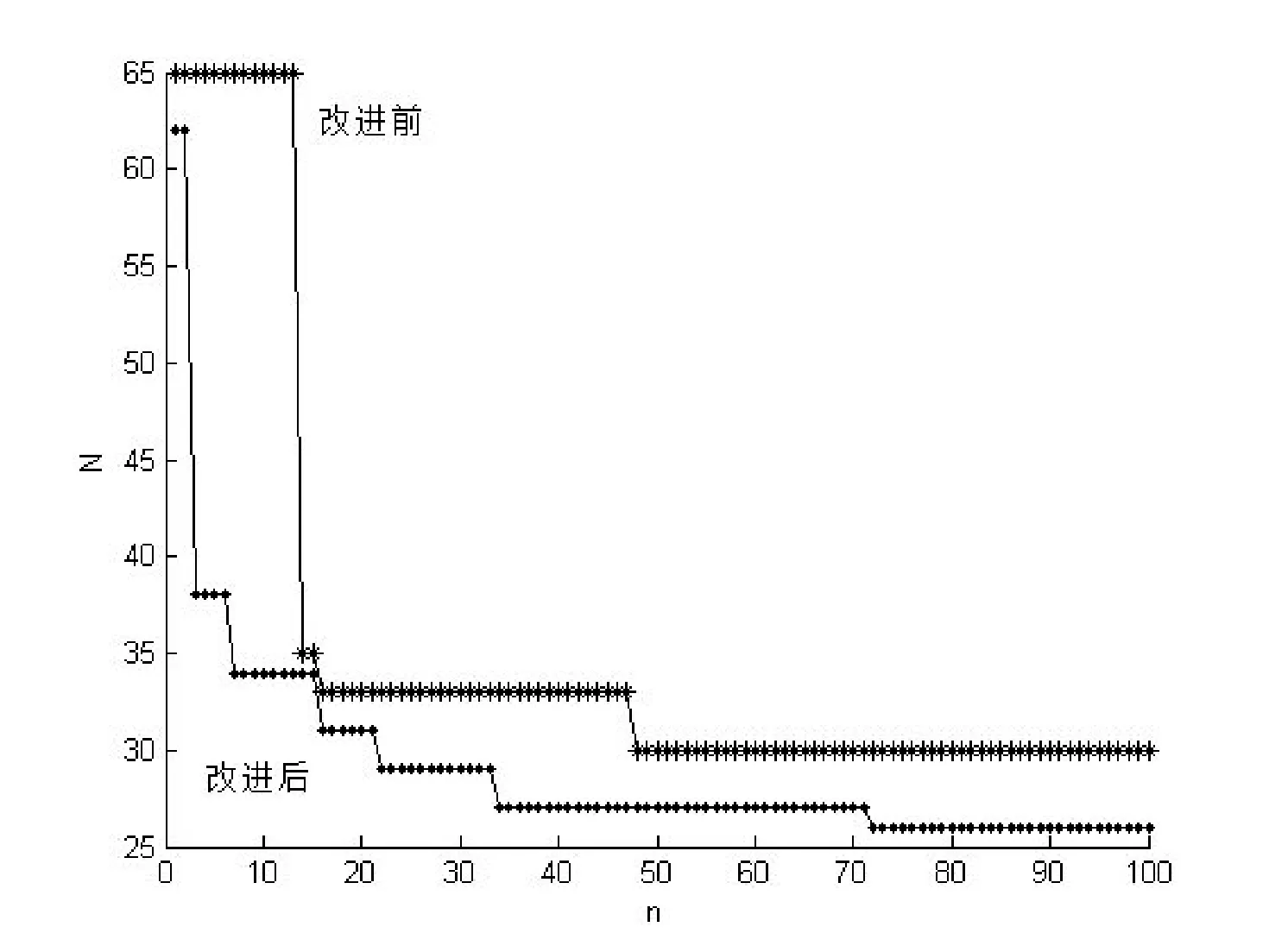



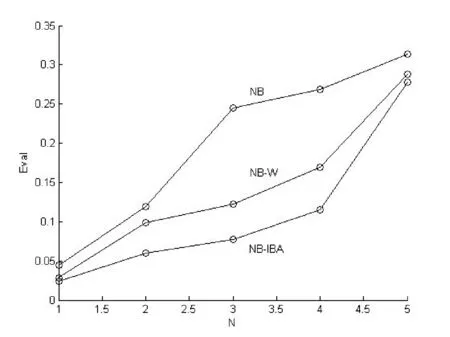
4 结 语

