基于(ε,ζ)-近似融合的无线传感网拓扑控制算法
汤 荣 郭 剑
(南京邮电大学计算机学院 江苏 南京 210003)
基于(ε,ζ)-近似融合的无线传感网拓扑控制算法
汤荣郭剑
(南京邮电大学计算机学院江苏 南京 210003)
对无线传感器网络的拓扑控制问题进行研究。为了节约网络能量,最大化网络生命周期,提出一种基于(ε,ζ)-近似数据融合的拓扑结构控制算法QGA-UQ(Quantum Genetic Algorithm-Unique Q)。QGA-UQ引入了节点调度的思想。它首先根据用户的数据精度要求,确定网络中工作节点的比例,接着再使用量子遗传算法,从网络中选取合适的节点,并形成合理的拓扑结构。网络在此基础之上进行数据的传输和融合处理。仿真试验表明,QGA-UQ算法可以在保证融合结果精度的前提下,显著延长了网络生存时间,提高了网络能量利用率。
拓扑控制无线传感器网络(ε,ζ)-近似融合节点调度量子遗传算法
0 引 言
近年来,随着计算机技术和传感器技术的发展和成熟,无线传感器网络WSNs(Wireless Sensor Networks)成为一个热门领域,引起了人们的广泛关注。无线传感器网络主要是由部署在监测区域内的大量传感器节点组成,通过无线通信的方式,形成一个多跳式的自组织网络。目前主要应用于医疗卫生、环境监测、灾难预防、生态保护、智能家居等各个领域[1-3]。
拓扑控制是无线传感器网络的核心技术之一,它主要通过节点调度、发射半径调节、通信链路选择等手段,优化网络的拓扑结构。通过拓扑控制技术,可以实现节约网络能量、提升网络通信性能等目标。在这方面,比较经典的工作是WBHeinzelman等人[4]提出的LEACH协议。为了减少数据传输的能耗,LEACH使用了簇结构,并在数据传输到基站前使用簇头节点来融合数据,但是它的簇头选取和数据传输策略存在一定问题,并且不能很好地兼顾到边缘节点。在LEACH算法的基础上,SDMuruganathan等[5]提出了BCDCP算法,采用迭代集群分裂算法选出多个簇头节点,用MST(Minimum Spanning Tree)结构连接簇头节点,保证任意两个节点之间都存在有向路径,这样整体拓扑结构较复杂,能耗偏大。较早提出用MST结构来连接拓扑的是Li N[6],其采用了MST结构来连接所有网内传感器节点,用MST-Z算法来调整拓扑,结构得到一定简化,但依旧能耗较大。同时,拓扑控制还需考虑其他问题,例如Nishiyama H等[7]研究了动态网络中的拓扑控制,Kim D等[8]控制拓扑时避免传感器节点监测区域的覆盖冲突。
在传感器网络的实际应用中,人们往往并不关心节点采集的具体数据,而是更关心宏观的统计结果,如一个地区的平均温度、最高湿度等,从而进行评估、决策等处理。这种情况下,就需要对网络的采集数据进行一定的融合处理[9,10]。由于网络拓扑不健壮、节点调度休眠等原因,网络往往会丢失部分采集数据,这时候,一些近似融合技术也就应运而生。ADeligiannakis等[11]和GHartl等[12]分别提出了基于时间的和基于空间的融合算法,它们在进行融合时不需要全部的数据,但是不能有效地控制误差范围。Sergiou C等[13]在近似融合过程中随机选定传感器节点作为活跃节点,用RANDOM-UQ算法控制节点的工作与休眠,数据精确性依旧得不到满足。Jianzhong Li等[14]提出的(ε,ζ)-近似融合算法,可以有效地控制融合的精度,但是它采用的网络拓扑并不是很好。
上述研究表明,为了达到通信性能、节能效果与融合精度的平衡,有必要将拓扑控制技术与数据融合技术结合起来进行研究。从这个角度出发,本文提出了一种基于(ε,ζ)-近似数据融合的拓扑结构控制算法QGA-UQ(Quantum Genetic Algorithm- Unique Q)。QGA-UQ基于节点调度的思想,它首先根据融合结果精度的要求,确定网络中休眠节点与工作节点的比例,接着再使用量子遗传算法,从网络中选取合适的节点,并基于MST树形成网络拓扑结构。网络在此基础之上进行数据传输和数据融合。上述过程可以循环进行,从而使节点轮流休息,达到延长网络生命周期的目的。实验结果表明,QGA-UQ算法较好地实现了设计的目标。
1 相关模型与假设
1.1网络模型
现有一块无线传感网的监测区域,该区域部署了大量的传感器节点,节点的部署方式为随机部署。所有节点同质,并且可以调节各自的发射功率。
假设网络初始时共有N个节点。在时刻t,无线传感网内存活节点的数目为Nt。依次对每次传感器节点进行编号,编号i从1到Nt。显然,当t=0时,Nt=N。
传感器节点i在t时刻对应的感知数据记为kti,把监测区域内所有活动节点的感知数据组合成一个数据集Kt,即Kt={kt1,kt2,…,ktNt}。考虑到任何实际感知数据都是有范围的,因此假定所有感知数据的上下界的值分别记为max(Kt)和min(Kt),并假设min(Kt)大于0。
本文假定,网络要求对监测区域内观测值的平均值Avg进行融合,并且融合结果要达到(ε,ζ)-近似估计的要求,(ε,ζ)-近似估计的精确定义将在第2节给出。
1.2能耗模型
本文使用了如下的能耗模型[15]。
无线传感网内的传感器节点在发送和接收1bit数据时都需要消耗能量,分别记为Ef和Ej。两者可通过以下公式计算:
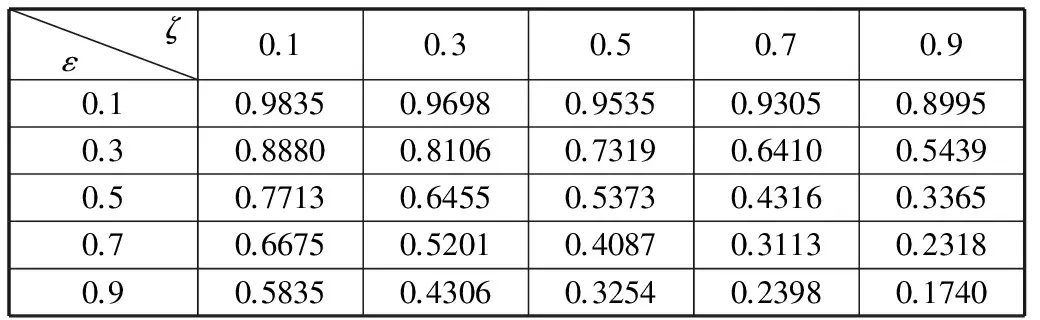
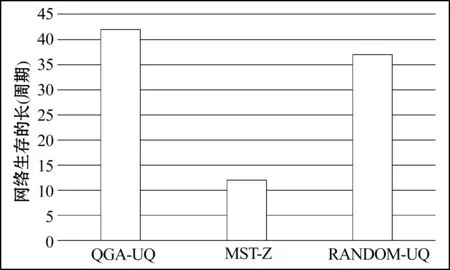
当d 而d≥d0时,Ef=Eelec+μampd4 Ej=Eelec 其中,d为该节点与相邻通信节点的距离,d0为收发两端的距离门限值,Eelec是发射电路与接收电路的能耗,μfs和μamp分别为慢衰落模型和快衰落模型的参数。 出于节能的考虑,当网络中的节点较多时,可以只让部分节点进入工作状态,以减少网络的能耗。但是另一方面,休眠的那部分节点也会导致采集数据的丢失,从而给数据融合的结果带来一定的误差。因此,活跃节点的比率q与数据融合的精度存在一定的约束关系。本节首先给出数据融合精度的相关描述,再给出q的计算方法。 关于近似融合,有如下定义[14]: (1) 假定在时刻t,网络采集的数据集为Kt,则此刻平均值Avg的融合结果为: 其中,inf(Nt)表示整个融合过程中无线传感网内活动节点数目的最低值,Φζ/4为标准正态分布的ζ/4分位值。 本文提出了基于(ε,ζ)-近似融合的无线传感网拓扑结构控制算法QGA-UQ,其总体思路是从网络中选择部分节点,并对这部分节点进行一定的运算处理,形成合适的拓扑结构。在拓扑调整过程中,控制每个传感器节点的休眠与工作状态,不同周期内选取不同传感器节点进行数据融合。 上一节主要讨论了选择节点的比例,这一节将讨论根据这个比例如何来选择节点并生成网络拓扑。由于无线传感网内传感器节点数目多、密度大,数据传输的能耗相当可观,因此网络拓扑的构建主要从节能角度来考虑。QGA-UQ采用MST结构[15]连接工作的传感器节点,计算的过程则采用了量子遗传算法[16]。 3.1染色体编码及测量 本文把拓扑结构的求解过程看作是量子遗传算法中的种群演化过程,每一代种群中含有若干条染色体。每条染色体表示当前无线传感网内所有节点的选择情况。如图1所示,染色体由一串二进制数字表示,长度等于无线传感网内传感器节点的总数,即染色体有N位。每一位数字0代表对应的传感器节点未被选取,1代表对应的传感器节点被选取。被选取的传感器节点参与数据信息的传输,以及数据融合工作,未被选取的传感器节点可以暂时休眠。 节点1节点2节点3节点4节点5节点6…节点N100110…1 图1染色体结构 染色体的测量与量子比特概率幅有关。根据量子比特和量子旋转门的调整,计算出相应的量子比特概率幅,每一周期的量子比特概率幅不同,测量染色体时,生成一个0到1之间的随机数,若随机数的值大于概率幅的平方,则染色体当前位的二进制数取1,反之,则染色体当前位取0。 3.2染色体评价 图2 MST结构示意图 对染色体进行评价必须从整个网络的拓扑结构考虑,图2所示就是MST树结构的例子。其中,图2(a)可以看到6个传感器节点,节点b是簇头节点,所有链路上标明的数字即为该段链路数据传输的权值。图2(b)是图2(a)对应的MST拓扑结构,它可以保证每个节点都能将数据传输到簇头节点b且网络总权值最小。 在此基础之上,本节把染色体的评价函数设为: f=αEs-βEx+γEmin 其中,α、β和γ是相应的系数,且它们都大于0。染色体评价函数主要考虑了如下三个方面: (1) 网络内所有节点的剩余能量之和Es,若第i个传感器节点的剩余能量为Ei,那么Es可由下式得到: (2) 网络内所有传感器节点消耗的能量总和Ex,可由下式计算得到: 其中Ei′是第i个传感器节点消耗的能量,该计算可以参考1.2节的能耗模型。 (3) 该方案中网络内所剩能量最少节点的能量Emin,由式(2)可得。加入该项分量是出于网络能量分布平衡性的考虑。 Emin=min{E1,E2,…,EqNt} (2) 3.3QGA-UQ的算法流程 (1) 网络初始化。在已知的监测区域范围,随机部署规定数目的传感器节点,并且将它们从1到N进行编号,设定观测数据值的上下界max(Kt)和min(Kt)。 (2) 结合(ε,ζ)-近似融合的要求,计算传感器节点工作比例q。 (3) 使用量子遗传算法计算出合适的网络拓扑结构。 (4) 网络运行一定周期。在该周期内,未被选中的节点进行休眠,选中的节点则进入数据采集和传输等工作状态,并由sink节点进行数据融合的处理和估计。 (5) 如果网络中的剩余节点少于qN,算法终止,否则转入(2)。 本节通过仿真实验验证QGA-UQ算法的性能。仿真基于VS2013平台,参数设置见表1。仿真时传感器节点位置随机部署。 表1 实验仿真参数设置 首先,我们通过改变(ε,ζ)-近似融合中的ε和ζ的值,统计传感器节点工作比例q的变化情况,表2是max(Kt)、min(Kt)分别为996和902时计算得出的结果。行代表ε,列代表ζ,数值代表的是传感器节点工作比例q。表中可以看出,ζ相同时,ε越大,传感器节点工作比例q越小,那是因为根据第2节定义1和2,ε越大融合结果容许的误差更大,所以节点工作比例不必那么大;ε相同时,ζ越大,传感器节点工作比例q也越小,同样也可根据第2节定义1和2分析出,ζ越大其实要求的数据精确度更低,所以只要抽样较少的传感器节点。ε和ζ越靠近0时,要求的数据精确率逐步达到最高,于是传感器节点工作比例q也越靠近于1。当ε为0.1、ζ为0.1时,传感器节点工作比例q达到0.9835。同时可以进一步发现,ε的值对q的影响较大。 表2 不同ε、ζ对应的传感器节点工作比例q 在研究QGA-UQ算法的优劣时,主要考虑以下两个方面:网络的生存时间和融合结果的相对误差。本文将QGA-UQ算法与如下两种算法进行对比:(1)MST-Z算法:基于总体进行数据融合处理,采用Prim算法的思想将所选节点用MST树结构连接,对拓扑结构进行调整优化。(2)RANDOM-UQ算法:基于概率抽样法进行数据融合处理,采用随机取点算法来控制拓扑结构。三种算法同时在ε和ζ都取0.3的情况下仿真比较。 本文中,网络生命周期定义为网络内存活节点数低于qN时所经历的周期数,其中假设传感器节点自身能量Es小于10 mJ时,该节点已死亡,不能再进入工作状态。从图3中可以看出,QGA-UQ算法下的网络生存时长最长, RANDOM-UQ算法次之, MST-Z算法下的网络生存时长最短。因此,MST树结构比随机拓扑结构更能延长网络生命周期。同时利用(ε,ζ)-近似融合来处理感知数据时,能极大地提高生存时长。 图3 三种算法的生存时间对比 在不同周期,对比三种算法融合结果与实际结果的相对误差,如图4所示,因为MST-Z算法是对无线传感网中总体的传感器节点进行数据采集,计算得出的Avg值没有误差。而其他两种算法由于是抽样采集,所以都存在不同程度的误差,但总体来看,均远远小于预期的容许误差0.3。 图4 三种算法融合结果的相对误差对比 综上所述,在本文比较的三个拓扑控制算法中,QGA-UQ算法在保证较低的融合结果相对误差下,网络生存时间更长并且整体网络能耗最少,是最优的一种拓扑结构控制算法。 为尽可能地监测无线传感网中的真实数据和减少整个网络的能耗,本文提出了一种基于(ε,ζ)-近似数据融合的无线传感网拓扑结构控制算法QGA-UQ。首先,根据(ε,ζ)-近似数据融合法计算出抽样传感器节点数目,然后利用量子遗传算法,通过种群染色体的不断演化,基于MST结构不断调整,最后得出最优拓扑结构。仿真实验表明,该算法对比已有算法表现出了良好的性能和稳定性。 [1] Luís M Borges.Survey on the Characterization and Classification of Wireless Sensor Network Applications[J].IEEE Communication Surveys & Tutorials,2014,16(4):1860-1890. [2] 孙利民,李建中,陈渝,等.无线传感器网络[M].北京:清华大学出版社,2005. [3] Corporation H P.Multihop-Based Optimal Cluster Heads Numbers Considering Relay Node in Transmission Range of Sensor Nodes in Wireless Sensor Networks[J].International Journal of Distributed Sensor Networks,2013,13(2):140-154. [4] Heinzelman W R,Chandrakasan A,Balakrishnan H.Energy-efficient communication protocol for wireless microsensor networks[C]//The 33rd Annual Hawaii International Conference on System Siences (HICSS-33),Maui,USA,IEEE,Los Alamitos,CA,United States,2000:3005-3014. [5] Muruganathan S D,Bhasin R I.A centralized energy-efficient routing protocol for wireless sensor networks[J].IEEE Communications Magazine,2005,43(3):S8-S13. [6] Li N,Hou J C,Sha L.Design and analysis of an MST-based topology control algorithm[J].Proceedings-IEEE INFOCOM,2002,4(3):1195-1206. [7] Nishiyama H.On minimizing the impact of mobility on topology control in mobile ad hoc networks[J].IEEE Transactions on Wireless Communications,2012,11(3):1158-1166. [8] Kim D,Noel E,Tang K W.WSN communication topology construction with collision avoidance and energy saving[C]//2014 IEEE 11th Consumer Communications and Networking Conference,CCNC 2014,Las Vegas,NV,United states,IEEE Computer Society,2014:398-404. [9] 牛淑芬,王彩芬,杜小妮.无线传感器数据融合技术中基于同态哈希函数的数据完整性算法[J].计算机应用与软件,2013,30(12):48-51. [10] Jose J,Manoj Kumar S,Jose J.Energy efficient recoverable concealed data aggregation in wireless sensor networks[C]//2013 IEEE International Conference on Emerging Trends in Computing,Communication and Nanotechnology,ICE-CCN,2013:322-329. [11] Deligiannakis A,Kotidis Y,Roussopoulos N.Processing approximate aggregate queries in wireless sensor networks [J].Information Systems,2006,31(8):770-792. [12] Hartl G.A Bayesian Inference Approach towards Energy Efficient Data Collection in Dense Sensor Networks[C]//25th IEEE International Conference on Distributed Computing Systems,Columbus,OH,United states,Institute of Electrical and Electronics Engineers Inc,2005:371-380. [13] Sergiou C.Source based routing trees for efficient comgestion control in wireless sensor networks[C]//8th IEEE International Conference on Distributed Computing in Sensor Systems,Hangzhou,China,IEEE Computer Society,2012:378-383. [14] Li J Z,Cheng S Y.(ε,ζ)-Approximate Aggregation Algorithms in Dynamic Sensor Networks.[J].IEEE Transactions on Parallel and Distributed Systems,2011,23(3):385-396. [15] 韩崇,孙力娟,肖甫,等.基于SVD的无线多媒体传感器网络图像压缩机制[J].东南大学学报:自然科学版,2012,42(5):814-819. [16] Huang G Y,Li X W,He J.Dynamic Minimal Spanning Tree Routing Protocol for Large Wireless Sensor Networks[C]//2006 1st IEEE Conference on Industrial Electronics and Applications,ICIEA,2006:1-5. [17] 孙力娟,郭剑,陆凯,等.基于量子遗传算法的传感器网络拓扑结构控制[J].通信学报,2006,27(12):1-5. A TOPOLOGY CONTROL ALGORITHM FOR WIRELESS SENSOR NETWORKS BASED ON (ε,ζ)-APPROXIMATE AGGREGATION Tang RongGuo Jian (School of Computer,Nanjing University of Posts and Telecommunications,Nanjing 210003,Jiangsu,China) We study the topology control of wireless sensor networks in this paper.In order to save network energy and maximise network lifecycle,we propose a (ε,ζ)-approximate aggregation-based topology control algorithm QGA-UQ (quantum genetic algorithm-unique Q).QGA-UQ introduces the idea of node scheduling.It firstly determines the proportion of working nodes in network based on user’s requirement of data accuracy.Then it uses quantum genetic algorithm to select appropriate nodes in network and construct a reasonable topology.On this basis the network carries out the operation of data transmission and data fusion.Stimulation tests show that QGA-UQ can prolong the survival time of the network significantly and improve the utilisation of network energy greatly on the premise of guaranteeing the precision of fusion results. Topology controlWireless sensor networks(ε,ζ)-approximate aggregationNode schedulingQuantum genetic algorithm 2015-04-17。中国博士后科学基金项目(2014M5516 35);江苏省博士后科研计划项目(1302085B)。汤荣,硕士生,主研领域:无线传感网。郭剑,副教授。 TP393 A 10.3969/j.issn.1000-386x.2016.09.0272 活跃节点比率的确定


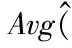
3 基于(ε,ζ)-近似数据融合的拓扑控制算法


4 仿真实验


5 结 语

