观测器/卡尔曼滤波在飞行数据处理中的应用
朱菲菲,高艳辉,肖前贵,胡寿松
(1.南京航空航天大学 自动化学院,江苏 南京210016;2.南京航空航天大学 无人机院,江苏 南京210016)
观测器/卡尔曼滤波在飞行数据处理中的应用
朱菲菲1,高艳辉2,肖前贵2,胡寿松2
(1.南京航空航天大学 自动化学院,江苏 南京210016;2.南京航空航天大学 无人机院,江苏 南京210016)
在无人机飞行参数测量中,受环境、干扰或自身稳定性等因素的影响,往往使测量数据中存在野值。为提高飞行数据处理精度,提出了一种基于观测器/卡尔曼滤波辨识(OKID)的新算法用于估计飞行参数。该算法直接利用输入输出数据与系统矩阵得到观测器增益,而观测器增益又收敛于稳定状态下的卡尔曼滤波增益,利用卡尔曼滤波增益即可估计飞行参数。Matlab仿真表明该方法能有效地消除飞行数据中的野值。
数据处理;观测器/卡尔曼滤波;观测器增益;野值剔除
在试飞过程中由于受到外界异常干扰、测量仪器或传输数据不稳定等多种因素的影响,导致测量数据严重偏离测量真值,这些偏离数据所呈现趋势的小部分数据集合,称为野值。野值的存在会给无人机的状态估计、性能导航及飞行性能分析带来较大的误差,甚至严重偏离飞机的飞行状态[1]。因此必须对野值进行处理,以保证数据处理精度。
目前,国内学者对测量数据的野值剔除方法已经有了大量研究,文献[2]利用多传感器数据形成的对目标状态参数的正确描述和测量数据集合主体的变化趋势,提出了分布式融合算法的野值剔除方法,检测效果较好但采用的Kalman滤波会出现滤波发散现象。文献[3-4,10]以“新息”为基础,通过重新构造Kalman滤波方法中增益矩阵的方法,对野值进行识别和处理,有效地解决了滤波发散问题。文献[5]提出了一种最小二乘算法与无迹卡尔曼滤波(UKF)结合的改进算法,当存在野值时利用最小二乘法近似曲线拟合估计预计状态值,不存在野值时利用UKF算法估计状态,为系统滤波提供了一种处理野值的实际解决方法,但该方法计算量较大。此外以上基于Kalman滤波的算法都需得知系统模型的过程噪声和测量噪声,而实际中很难精确地得到系统的测量噪声和过程噪声特性。
文中提出了一种基于观测器/卡尔曼滤波辨识 (OKID)处理飞行试验数据中野值的方法[6-9],该方法直接由输入输出数据与系统矩阵信息得到观测器增益,结合观测器与卡尔曼滤波之间的关系及观测器增益,最终得出稳定状态下的卡尔曼滤波增益[6],从而利用卡尔曼滤波增益估计飞行数据的正确状态。该方法不需得知系统过程噪声和测量噪声协方差矩阵,通过仿真验证表明该方法可有效地对野值进行剔除与补正。
1 算法描述与实现
1.1 观测器/卡尔曼滤波辨识(OKID)算法考虑如下多变量离散时间线性系统:

式中x(k)为n×1维向量,y(k)为p×1维向量,u(k)为m×1维向量,A,B,C,D为维数适当的系数矩阵。假设该线性系统初始状态为零,即x(0)=0,则可得到如下方程组,其中k=0,1,…,l。

式(2)可表示为矩阵形式:


式(3)建立了系统(1)输入与输出历史数据间的关系。其中y∈RP×l,Y∈Rp×ml,U∈Rml×l,l为数据采样的长度,p为系统输出变量的个数,m为系统输入变量的个数。矩阵Y包含了所有的待定的Markov参数CB,CAB,CAl-1B。
当系统状态未知时,观测器通常根据已知的输入输出信息估计状态。因此,式(1)加上并减去Fy(k)项,系统(1)的观测器可写为:
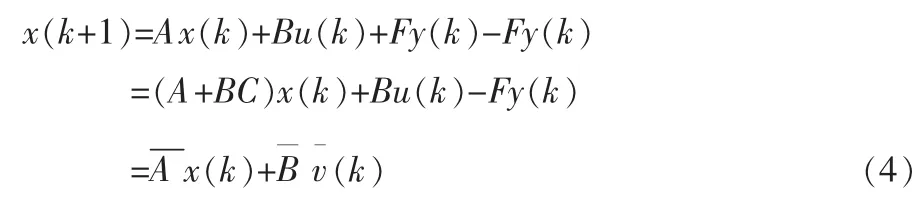

则测量方程可写为:

其中:


其最小二乘解为:


则利用式(10)与已知的系数矩阵A,B,C可求解出满足一定条件的观测器增益矩阵。
1.2 观测器与卡尔曼滤波之间的关系
系统(1)可描述为包含过程噪声和测量噪声的如下系统:

其中w(k)为服从高斯,零均值白噪声分布的过程噪声,v(k)为满足同样条件的测量噪声。且w(k)与v(k)序列互相独立。则系统(11)的典型卡尔曼滤波为:
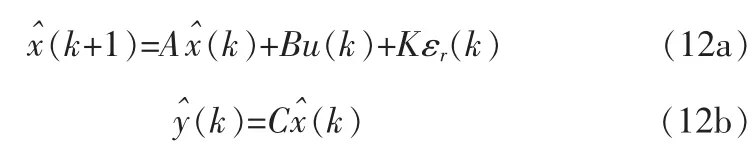

测量方程变为:

当F=-K且εr(k)=0时,式(4)与式(13)是等价的,事实上任何满足最小二乘解的观测器都将生成与卡尔曼滤波相同的输入输出映射关系,假设数据长度足够大,则截断误差[7]可忽略。因此残差εr(k)为卡尔曼滤波残差的白噪声序列,观测器增益矩阵F收敛于稳定状态的卡尔曼滤波增益K[6-8]即F=-K。
1.3 野值的识别、剔除与补正
利用由观测器得到的卡尔曼滤波增益K来预测系统观测量的估计值ˆ(k),构造新息,按时间顺序逐点计算及新息vi。对于野值,其新息值vi远大于正常值,可采用下式为准则[11]来判别野值。

为保证数据的完整性,当识别和剔除野值点后,需对剔除后的野值点进行补正。野值的补正利用估计值代替。
2 仿真与结果分析
仿真数据采用某型无人机的试飞数据,数据采样周期为40ms,由于磁航向角易受外部磁环境影响,导致测量数据含有野值,因此以磁航向角试验数据为例,分别在试验数据中加入独立分布与连续分布的野值,利用Matlab软件进行仿真。
建立单输出、零输入系统的离散化状态方程和观测方程模型,如式(15)所示:

选取数据采样长度l为2 000,q为400,利用Matlab软件根据输入输出数据由式(9)可得到观测器的Markov参数矩阵。由于矩阵为零,则式(10)变为:

在第40 s、44 s、48 s单独加入3个不等的野值,其幅值在原幅值的1~2倍之间。仿真结果如图1所示。在第40 s开始加入满足同样幅值条件的10个连续野值。仿真结果如图2所示。

图1 磁航向角测量数据独立野值处理
以上仿真结果表明利用观测器/卡尔曼滤波辨识得到的稳定卡尔曼滤波增益可以很好地对系统进行预测,当数据出现野值时即可利用估计值来处理野值,从而有效地抑制了飞行试验数据中野值的影响。

图2 磁航向角测量数据连续野值处理
3 结 论
实际工程实践中,由于多种因素的影响,飞行试验测量数据中野值的出现是不可避免的,传统的滤波算法不具备处理野值的能力,当出现野值时,将会对测量数据进行错误估计从而偏离正确值,甚至导致滤波发散。如何有效地克服Kalman滤波器在出现野值的情况下引起的发散现象和误差较大严重偏离真值的情况,在工程应用中是非常重要。
文中介绍了一种基于观测器/卡尔曼滤波的方法处理飞行试验数据中的野值,该算法利用稳定状态的卡尔曼滤波增益对系统进行估计,避免了出现野值时,调整卡尔曼滤波增益无法得到正确估计值的问题,此外该算法不需得知系统的过程噪声和测量噪声,简单易行。为飞行试验数据野值处理提供了一种解决方法。
[1]王鹏伟,吴秀清,余珊.基于角点特征和自适应核聚类算法的目标识别[J].计算机工程,2007,33(6):179-181.
[2]贺明科,王正明,朱炬波.多传感器目标跟踪的实时剔野方法[J].宇航学报,2002,23(6):34-37.
[3]祝转民,秋宏兴,李济生,等.动态测量数据野值的辨识和剔除[J].系统工程与电子技术,2004,26(2):147-149.
[4]Peng Yang,Hairrong Sun,LinanZu,et al.Adaptively target trackingmethod based on double-Kalman filter in existence of outliers[J].IEEE International Conferenceon Roboticsand Biomimetics(ROBIO),2010:950-954.
[5]徐利娜,陈俊彪,穆高超.靶场外弹道数据处理中的实时野值剔除算法[J].应用光学,2012,33(1):90-95.
[6]Tsai S H,Hu N T,Yang P C,et al.Modeling of decentralized linear obse-rver and tracker for a class of unkno-wn interconnected large-scale sampled-data nonlinear systems with closed-lo-op decoupling property[J].Computers&Mathematicswith Applications,2010,60(3):541-562.
[7]Wu C Y,Tsai S H,Guo S M,et al.A novel on-lineo
bserver/Kalman filter identification method and its application to input-constrained active fault-tolerant tracker designfor unknown stochastic systems[J].Journal of the Franklin Institute,2015,352(3):1119-1151.
[8]Majji M,Juang JN,Junkins J L.Ob-server/Kalman-Filter Time-Varying System Iden-tification[J].Journal of Guidance Control&Dynamics,2010,33(3):887-900.
[9]Corporation H P.Detection of Sensor Faults in Small Helicopter UAVs UsingObserver/Kalman Filter Identification[J].Mathematical Problems in Engineering,2011,6(6): 505-515.
[10]张强,孙红胜,胡泽明.目标跟踪中野值的判别与剔除方法[J].太赫兹科学与电子信息学报,2014,12(2):256-259.
[11]赵志刚,吕恬生.小型无人直升机辨识建模试验信号的预处理[J].兰州交通大学学报,2010,29(4):40-43.
[12]Heredia G,Ollero A.Detection of Sensor Faults in Small Helicopter UAVs Using Observer/Kalman FilterIdentification[J].Mathematical ProblemsinEngineering,2011,6(6):505-515.
Application of observer/Kalman filter in flight data processing
ZHU Fei-fei1,GAO Yan-hui2,XIAO Qian-gui2,HU Shou-song2
(1.College of Automation Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China;2.Research Institute ofUnmanned Aircraft,Nanjing University of Aeronauticsand Astronautics,Nanjing 210016,China)
Affected by the environment,interference or its stability,the outliers often exists in the flightdatameasurement.In order to improve the flight data processing accuracy,annew algorithm based on the observer/Kalman filter identification(OKID)is proposed to estimate the flight parameters.The algorithm directly uses the input and output data and the system matrix to obtain the observer gain,while the observer gain converges to the steady-state Kalman filter gain.This Kalman filter gain can be used for flightparametersestimation.Matlab simulations show thismethod can effectively eliminate the outliers in flightdata.
dataprocessing;observer/Kalmanfilter identification;observer gain;outlier elimination
TN957.51
A
1674-6236(2016)20-0091-03
2015-10-26 稿件编号:201510177
朱菲菲(1990—),女,河南许昌人,硕士研究生。研究方向:无人机建模与仿真。

