一种基于模型分割的三维人体骨架提取方法
甘凌云 侯 进,2*
1(西南交通大学信息科学与技术学院 四川 成都 611756)2(南京大学计算机软件新技术国家重点实验室 江苏 南京 210093)
一种基于模型分割的三维人体骨架提取方法
甘凌云1侯进1,2*
1(西南交通大学信息科学与技术学院四川 成都 611756)2(南京大学计算机软件新技术国家重点实验室江苏 南京 210093)
针对当前三维骨架提取方法复杂度较高、提取结果不够准确,以及专门针对人体模型的方法较少等问题,提出一种基于模型分割的三维人体骨架提取方法。首先,根据模型顶点与末端特征点的最小测地距离将模型分割;然后由归一化的测地距离函数确定模型各顶点所属拓扑层次;接着在模型分割的基础上依据拓扑层次提取出原始骨架点;最后经过微调,将各骨架点按照拓扑关系连接得到较为精确的人体骨架。实验结果表明,该方法有效降低了骨架提取算法的复杂度,且对不同姿势的人体模型均可获得较为准确的提取结果。
骨架提取模型分割测地距离拓扑层次
0 引 言
虚拟人作为人类在虚拟世界中的化身[1],自然成为模拟人类行为的最好工具。而当前众多领域例如行为识别[2]、影视制作、游戏及动画的大量研究都是基于骨架进行的。骨架作为三维对象几何和拓扑结构的简化表示[3],不仅保留了模型的原始形态特征,而且减少了冗余信息,压缩了存储空间,经常被用在形状分析[4]、曲面重建[5]、骨骼动画[6]、模型检索[7]等研究当中。这一切使得对虚拟人和骨架的相关研究相互依赖、共同发展,所以如何从三维人体模型中提取出有效的骨架信息,成为近年来专家学者们潜心研究的重要内容。
一方面,一些三维扫描设备可以直接提取出主要关节的大概位置[8],但得到的结果往往无法达到准确和全面的效果。另一方面,研究人员针对骨架所具有的特点,也纷纷在不同理论的基础上提出了相应的骨架提取方法。例如,Au等[3]人通过全局位置约束使得模型收缩,直到得到一副零体积的骨骼线。徐超等[9]采用基于距离变换的方法,通过局部比较快速确定候选骨架点,再经过一定的规则约束生长出骨架。Jiang等[10]人使用基于Voronoi图计算的方法使骨架图收缩,并通过表面聚类确保收缩过程中的均匀性。但是,这些方法多是从通用的模型中提取出骨架信息,所以有些并不适用于人体结构,而且容易受到模型姿态等因素的影响。关华等[11]基于三角简化的方法得到人体模型的Reeb图,再通过计算Reeb图上各节点的曲率来添加关节点,最终实现模型的骨架提取。吴伟和等人[12]以特征点为起点计算模型等测地线的中心线,再根据人体测量学知识确定关节点的近似位置。他们虽然针对人体模型提取出了较为准确的骨架结构,但是计算过程较为复杂,在实现上有一定的难度。刘辉[13]采用测地距离计算简化模型的特征点,再根据特征点划分顶点分支并删除多余骨架点生成最终骨架。该方法有效降低了算法复杂度,但存在提取骨架不够精细的问题。
鉴于基于Reeb图的方法对于模型的旋转、平移具有很强的鲁棒性,且有较强的抗噪性能,相对于其他方法也更加简单易行,非常适用于像虚拟人这样对称且具有规则拓扑结构的对象。本文在Reeb图的启发之下,以模型分割为基础,通过综合分析人体模型的特征点域以及拓扑层次结构来确定骨架点,从而提取出满足人体结构特点的骨架。实验结果与对比表明,本文方法不仅简单易行,而且对于不同姿势的人体模型都能得到较为精确的提取效果。
1 算法概述
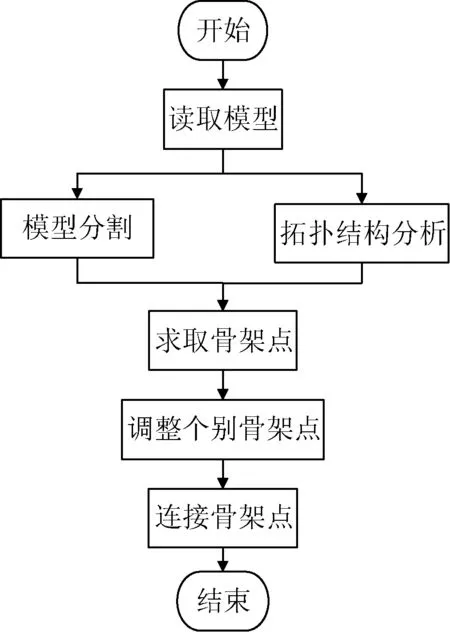
图1 算法过程示意图
本文借鉴Reeb图的思想,在模型分割的基础上对三维虚拟人三角网格模型进行骨架提取。在模型分割阶段,利用各顶点到人体末端特征点的测地距离计算特征点域。然后利用归一化的测地距离函数计算出每一顶点的分类函数值,为下一步提取骨架点提供重要的拓扑层次信息。接下来综合分析以上两步得到的结果,通过算法获得原始骨架点。最后对个别骨架点进行调整,并根据模型的拓扑结构连接相应节点完成最终的提取工作。整个方法计算复杂度低、提取结果较为精准,适用于不同姿势的人体模型,具有很好的可推广性。其具体算法过程如图1所示。
2 模型分割
2.1特征点的提取

图2 特征点所在最小区域示意图
一般将三维网格模型中局部突出的点作为特征点,它反映了整个模型的空间结构以及分支情况。本文分别将目标特征点所在的最小区域单独命名,在将模型整体导出后,以顶点索引特征为判断依据搜索出目标特征点。
假如目标特征点所在的最小区域是由图2的形式构成,四边形BCDE(当然也可能为其他多边形)为模型内部不封闭的部分。如果顶点A、B、C、D、E的索引号依次为0、1、2、3、4,那么△ABC、△ACD、△ADE和△ABE的构成索引对就如表1所示。
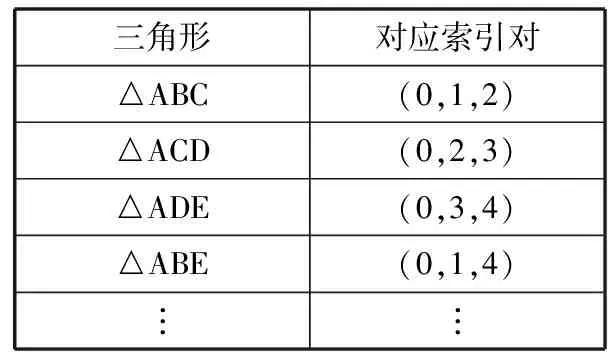
表1 三角形及其索引对
由表1可以明显看出,具有局部突出特征的点A在构成每个索引对中均作出贡献。所以只要遍历目标特征点所在最小区域的全部三角形,找出在每个三角形中均有出现的索引,即可确定该索引所代表的顶点为目标特征点,其三维坐标等信息也就继而得知了。本文以此方法分别提取出位于人体头顶、左指尖、右指尖、左脚尖和右脚尖的5个顶点作为特征点参与后续计算。
2.2基于特征点的结构分割
2.2.1特征点域
本文模型满足下式:
D={vn|f(vn)=g(vfp),n∈(0,N)}
(1)
其顶点集合称为对应特征点的特征点域。其中,vn为模型的第n个顶点 ,vfp为某一特征点;f、g分别是以vn和vfp为变量的函数,N为模型的总顶点数。
根据以上定义可知,特征点域即为具有某种相同函数特征的顶点集合,处在相同域内的顶点与对应特征点之间存在某种特殊联系。而正是由于特征点有着描述模型局部特征的功能,所以在以特征点为参照得到的顶点集合内部也将有着相类似的某种联系。这样以特征点为依据对模型进行划分,将为后续的骨架提取提供重要的模型结构信息。
2.2.2特征点域的计算
鉴于特征点常位于极值部位,很容易使人联想到将模型顶点与特征点间的距离作为分割依据。然而由于三维模型的空间特殊性,若直接使用欧式距离,很多时候并不能得到正确的分割结果,所以考虑采用各顶点到相应特征点的测地距离作为划分标准。
测地距离是指沿表面两点之间最短路径的长度,通常可用迪科斯彻(Dijkstra)算法来近似计算。与欧式距离相比,测地距离兼顾了曲面上两点之间的几何连通性,因此可获得更加合理的分割效果。
Dijkstra算法的主要思想如下:
(1) 选择一个基准点b,令集合S={b},T={模型剩余点},T中顶点vi(xi,yi,zi)若可直达b(xb,yb,zb),则距离g(vi)=dis(b,vi),否则g(vi)=+∞;
(2) 判断T是否为空,是则转至步骤(4),否则从T中选取一个与b有最小距离的顶点vj,并将此点加入S;
(3) 若T中顶点vk到b的距离大于途经vj再至b的距离,即:
g(vk)>g(vj)+dis(vj,vk)
(2)
则更新:
g(vk)=g(vj)+dis(vj,vk)
(3)
同时转至步骤(2);
(4) 此时所有顶点都包含在S内,它们与b之间的距离g(vi)即为所求最短路径。
其中:
(4)
(5)
以各特征点为基准点,采用Dijkstra算法求得模型顶点与各特征点之间的最短路径,将与各特征点有最小测地距离的顶点分别聚合,即可得到各特征点域。相同域的顶点与相应特征点在几何表面都有着最为快捷的到达方式。这种到达方式将三维模型分割成与特征点数目相同的几个部分,构成模型局部独立的几大分支,而准确的分支信息将成为确定骨架点的一大依据。
3 人体模型拓扑结构分析
3.1Reeb图
Reeb图是三维模型拓扑结构的一种重要描述方式,由定义在一个任意维度对象上的连续标量函数确定[14],是数学家Georges Reeb为分析流形拓扑结构而首先提出,常被用于计算几何、计算机图形学等科研领域。
Reeb图的定义:假设有一流形M,f是定义在M上一个连续而光滑的函数,R是M经由f生成,即f:M→R。对于xi,xj∈M,如果f(xi)=f(xj),那么R是M在f的映射下生成的Reeb图。
本文在这种思想之下,不同于一般基于Reeb图的方法那样对大量等值线提取中心连成曲线骨架线,而是由分类函数f对人体进行拓扑计算,再通过参数控制拓扑层次直接提取骨架点,从而减少了一定的计算量。
3.2分类函数的选取
高度函数、测地距离和调和函数等都常被用来作为f函数。由于测地距离沿网格表面计算两点间的最短距离,所以在不同姿势和体态下具有更大的优势,十分有利于得到准确的分类结果。所以本文在这部分仍然沿用模型分割时特征点域内各顶点与相应特征点间的测地距离函数进行拓扑划分。同时为便于计算统计,采用归一化后的测地距离,如下所示:
(6)
其中,g(vi)为vi与对应特征点的测地距离,max{g(vj)}、min{g(vj)}分别为测地距离的最大值与最小值,N为模型顶点数。
3.3拓扑层次的分析

而对于K的取值,如果选择最小值1,那么整个模型将属于同一拓扑层次,此时就失去了表达人体拓扑信息的意义。随着K取值的增大,相应的拓扑层次也将不断增加,而过多的层次对于描述人体骨架结构也是没有帮助的,反而会减慢计算速度。所以,是否合理地选择K的取值,会在很大程度上决定最终实验效果的好坏。
图3从左到右、从上至下依次为K=2~7时一个男性人体模型的拓扑层次结构,分别使用不同的深度表示具有同一拓扑特征的顶点集合。由图可见,随着K值的不断增大,拓扑层次也在不断增多。当K=2时,人体模型各部分只是被粗略地区分,这样提取出的骨架点将较为稀疏;而K=7时,各部分的划分又过于细致,这时不仅会增加计算量,而且还可能出现由于划分过细而提取出孤立点的情况。经反复试验发现,当K=4时,人体各部分的层次划分较为合理,提取出的骨架点位置也与真实人体关节较为接近,而此时计算复杂度也相对较低。

图3 不同K值下的人体拓扑层次
4 人体模型骨架提取
4.1骨架点的求取
为得到能够反映模型结构特点的骨架点,刘辉[13]使用改进的拓扑结构法遍历所有网格顶点,以相邻点与当前点的特征点域情况判断当前点是否为分支点,进而将同一分支集合内的顶点聚合求得骨架点。改进的拓扑结构法适用于存在孔、洞的模型,避免了处于同一水平集而不同分支内的顶点聚合为同一骨架点的情况。但是由于此种方法只依据特征点域进行分支判断,所以最终得到的骨架点只存在于模型分支处,不免显得较为稀疏,可能无法将模型的结构特点作详尽描述。另外,该方法得到的骨架还有可能出现环路,这时就不得不对骨架进行再次加工。而本文采用综合分析模型分割结果及拓扑层次的方法,对每一分支内具有相同拓扑层次的顶点聚合,逐层求解的过程避免了环路的发生,得到的骨架点数量更利于反映模型的结构特点,对于人体模型来讲具有更为丰富的描述意义。本文求取骨架点的具体算法步骤如下:
(1) 将不同水平集内的顶点按f值分K类存放;
(2) 遍历其一水平集内的所有顶点,如已处理完毕则转至(5),否则将未处理顶点v入栈S;
(3) 取栈顶元素vt,遍历其邻点是否与vt在相同的水平集,是则返回(2),否则继续;
(4) 将vt添加到vt的骨架点数组,重新遍历其邻点,将与vt在同一水平集的邻点入栈S,转(3)至栈空;
(5) 对其余水平集重复(2)至(4);
(6) 遍历每一骨架点数组中顶点是否具有相同特征点控制域,是则结束,否则继续;
(7) 将具有不同特征点控制域的骨架点数组分离为新的骨架点数组,至此得到基于模型分割的各部分骨架点数组。
最后,将每一骨架点数组中的顶点作坐标平均,得到所求三维模型的所有骨架点,如式(6)-式(8)所示,此时提取骨架点满足骨架对于中心性的要求。
(7)
(8)
(9)
式中xvj、yvj、zvj为顶点vj的三维坐标,Ni为第i个骨架点数组中的顶点总数;xi、yi、zi为第i个骨架点的三维坐标,M为骨架点总数。
4.2个别骨架点的调整

图4 肩、踝骨架点调整前后对比
实验发现,本文方法对于人体模型肩关节和踝关节附近的骨架点提取效果有时并不十分理想。究其原因是由于肩、踝部的几何结构不规则所致,所以还需对不够精确的骨架点进行位置调整。本文以0.01为步长,将提取的原始骨架点沿需要调整的坐标轴方向移动,直至到达合适的位置。图4即为这两部分骨架点位置调整前后的对比示意图。
5 实验结果及讨论
本文实验是在Windows 7,Intel Core i5-3230M CPU,2.6 GHz,2.88 GB的环境下,利用OpenGL图形库,以Visual Studio 2010作为软件开发平台进行的。选取的人体模型共有3个,其中2个从Poser8中导出,分别为男性人体模型Nude Man P4 Lo和女性人体模型Nude Woman P4 Lo。另有一自建模型用于检测骨架驱动效果,进而评价本文方法的实际应用价值。三者皆选头顶和四肢肢端共计五个顶点为特征点。除人体模型之外,本文也对Poser8中的2个非生命体做了同样实验,各实验模型数据如表2所示。

表2 实验模型相关数据
图5和图6即为对Nude Man P4 Lo进行特征点提取和模型分割的结果。图6采用不同深度标记模型具有同一分类特征的顶点集合,可以明显看出整个模型被分为5个部分,正好对应于所选取的5个末端特征点。
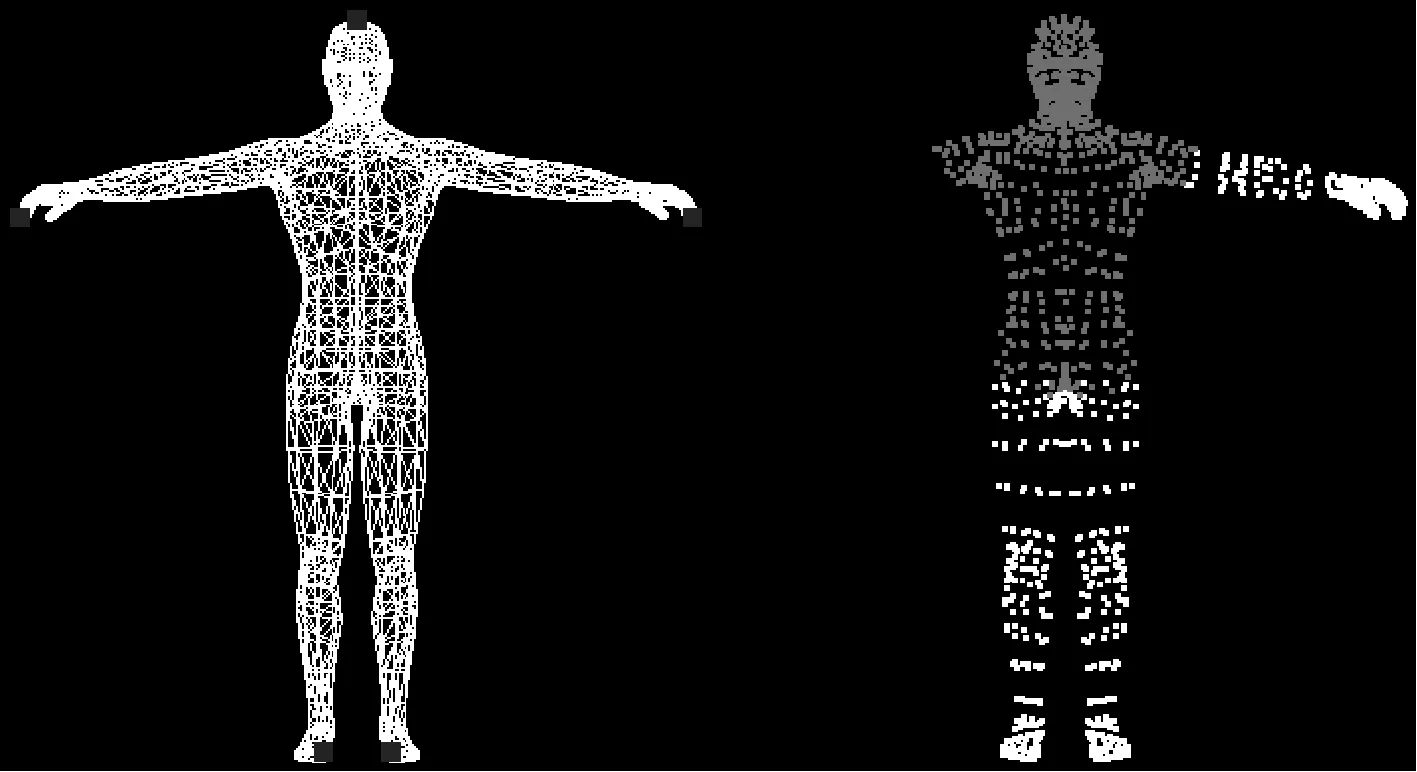
图5 特征点提取结果 图6 模型分割结果
图7是文献[13]中改进拓扑结构法的骨架提取效果。从(a)-(c)的人体模型来看,一方面,提取的分支节点较为稀疏,造成骨架结构十分简单;另一方面,对于双手平举的模型,虽然从正面看来可以取得形象的骨架效果,但是从俯视图来看就暴露了骨架穿出皮肤的缺点。对于双手下垂的模型来讲,从正面就能看到其骨架并没有位于模型之内。对于(d)和(e)的非人体模型也同样或多或少地存在类似现象。

图7 文献[13]方法的骨架提取结果
本文方法由于是在模型分割的基础上按照拓扑层次逐层求取骨架点,所以不会出现骨架在模型以外的情况,具体结果如图8所示。从人体模型(a)-(c)可见,无论是在骨架点数量还是骨架形态上,本文方法所得结果更适合描述人体的结构特点,具有更为细致的提取效果。
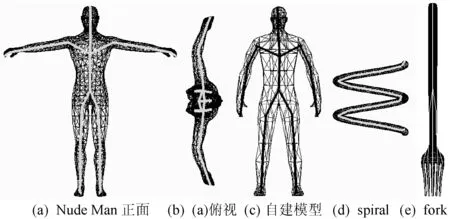
图8 本文方法的骨架提取结果
表3对文献[13]与本文方法所提取的骨架点数量进行了比较。从表中亦可以看出,本文方法获得的骨架点更多、更细致,所以在模型的细节描述上具有更大的优势。
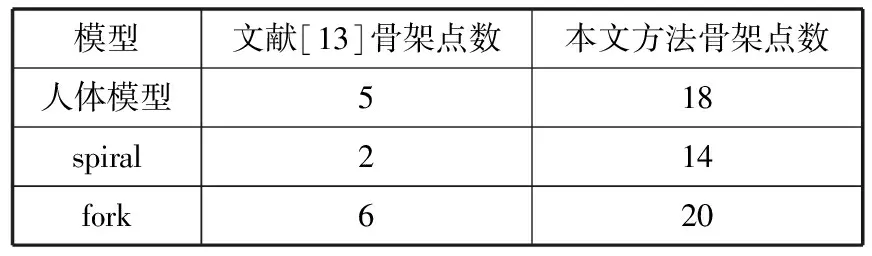
表3 骨架点提取数量对比
图9是针对女性模型在不同姿势下进行骨架提取,因为借鉴了Reeb图的思想并充分考虑人体拓扑结构特点,所以本文方法同样受人体姿势变换的影响较小。实验结果证明,本文方法不仅对于标准姿态的人体模型能够提取出形象的骨架,还适用于不同姿势的三维人体模型,且都能够得到较为理想的结果。

图9 女性模型不同姿势的骨架提取结果
最后,为说明本文方法所得骨架可应用于骨骼动画,采用顶点混合绑定的方法使得骨骼可以对虚拟人皮肤进行驱动,绑定权重由骨骼投影法作粗略估计。图10为虚拟人从初始姿势到迈步状态的一个动作效果,可见当自建模型的骨架做出一定量运动之后,皮肤也会随之发生变化。动画效果充分说明本文提取骨架较为合理,能够驱动虚拟人产生生动逼真的骨骼动画,这部分也将是下一步研究的一个重点。
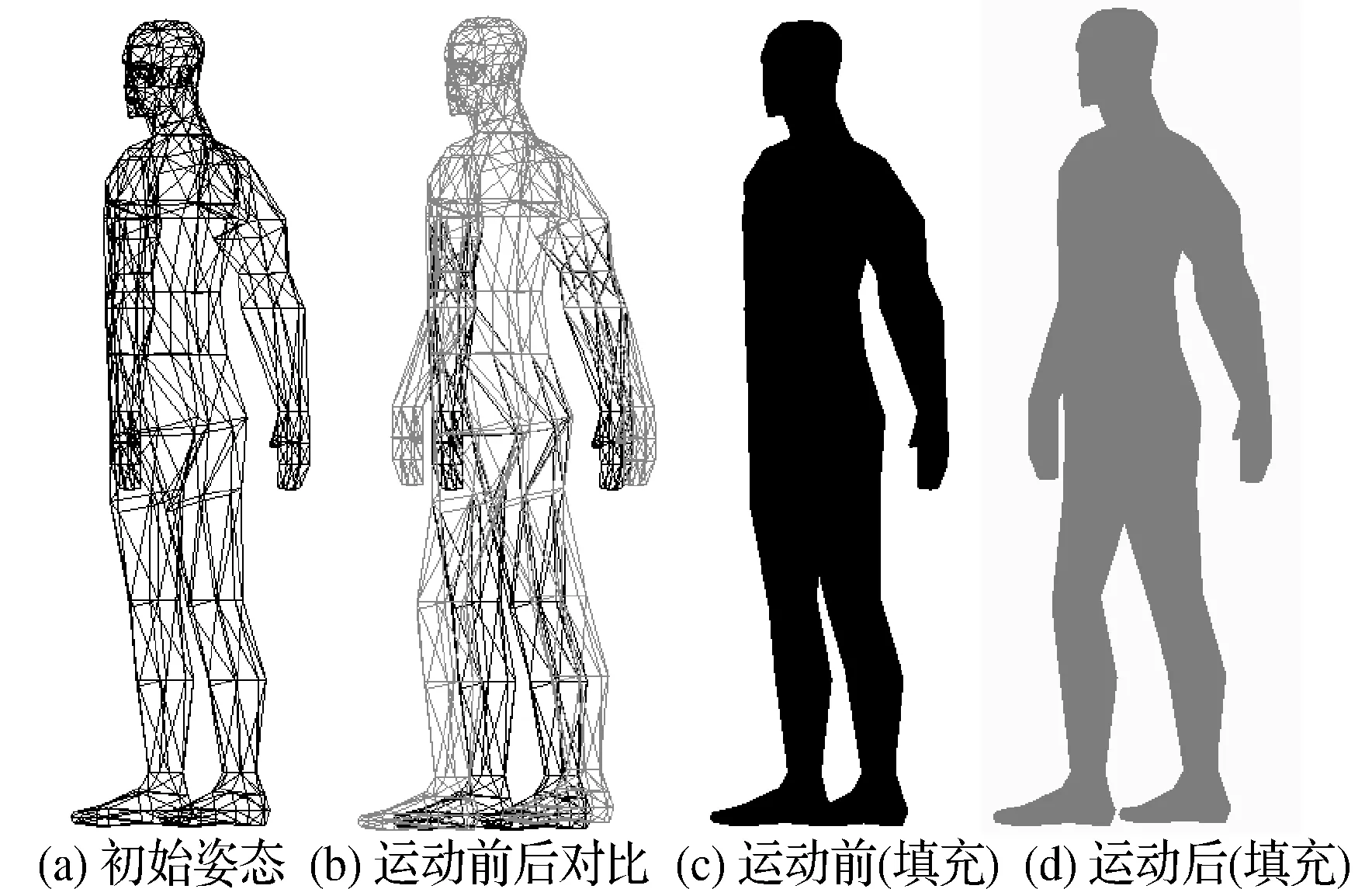
图10 腿部蒙皮后的动作效果
6 结 语
本文提出一种基于模型分割的三维人体模型骨架提取方法,使得提取结果更加适用于虚拟人三维模型,并且对于不同姿势都能得到较为精确的提取效果。首先通过计算每个顶点到特征点的最短路径来划分特征点域分割模型;然后根据各顶点的分类函数值将三维模型进行拓扑层次的构造;接着依据模型分割结果和拓扑结构提取出更为精确和丰富的骨架点;最后连接具有相邻关系的节点得到最终提取结果。不同于一般先求取中心骨架线的方法,本文方法更加简单易行,并且效果显著。下一步的工作重点在于:(1)对于非人体模型而言,本文方法有可能会出现骨架点提取过于细致的问题,如图8(e)所示,所以还需对非人形模型骨架点的精简展开研究;(2)进一步深入探索,使本文骨架提取结果能够应用于动作识别或者骨骼动画等。
[1] Hou J, Xu F, Wu L, et al. Avatar-based human communication: a review[J].International Journal of Modelling and Simulation, 2012, 32(4): 273-278.
[2] Du J, Chen D F. 3D action recognition based on limb angle model[C]//2014 4th IEEE International Conference on Information Science and Technology. Shenzhen: IEEE, 2014:304-307.
[3] Au O K C, Tai C L, Chu H K, et al. Skeleton extraction by mesh contraction[J]. ACM Transactions. on Graphics, 2008, 27(3):441-449.
[4] Li Z, Qin S W, Yu Z Y, et al. Skeleton-based shape analysis of protein models[J].Journal of Molecular Graphics and Modelling, 2014, 53:72-81.
[5] Agarawal M, Kumar S, Bala A. Three dimensional object retrieval using a skeleton-based approach[C]//2014 IEEE International Advance Computing Conference. Gurgaon: IEEE, 2014:1147-1151.
[6] Pantuwong N, Sugimoto M. A novel framework for 3D computer animation systems for nonprofessional users using an automatic rigging algorithm[C]//2012 IEEE International Conference on Multimedia and Expo. Melbourne: IEEE, 2012: 896-901.
[7] 韩丽, 程远. 融合骨架结构与几何细节的三维模型检索方法[J]. 计算机应用与软件, 2013, 30(11):199-201,273.
[8] Wang S X, Qin S F, Guan C Y. Feature-based human model for digital apparel design[J]. IEEE Trans. on Automation Science and Engineering, 2014, 11(2):620-626.
[9] 徐超, 肖潇, 骆燕,等.基于距离变换的新型骨架提取方法[J]. 仪器仪表学报, 2012, 33(12):2851-2856.
[10] Jiang W, Xu K, Cheng Z Q, et al. Curve skeleton extraction by coupled graph contraction and surface clustering[J]. Graphical Models, 2013, 75(3):137-148.
[11] 关华, 郭立, 李文,等. 一种人体三维Reeb图计算方法[J]. 计算机工程, 2011,37(19):207-209.
[12] 吴伟和, 郝爱民, 赵永涛,等. 一种人体运动骨骼提取和动画自动生成方法[J]. 计算机研究与发展, 2012, 49(7):1408-1419.
[13] 刘辉. 基于Reeb图的三维网格模型骨架提取算法研究[D]. 济南:山东师范大学, 2013.
[14] Hachani M, Zaid A O, Puech W. Segmentation of 3d dynamic meshes based on Reeb graph approach[C]//2014 Proceedings of the 22nd European Signal Processing Conference. Lisbon: IEEE, 2014: 2175-2179.
A METHOD FOR EXTRACTING 3D HUMAN BODY SKELETON BASED ON MODEL SEGMENTATION
Gan Lingyun1Hou Jin1,2*
1(School of Information Science and Technology, Southwest Jiaotong University, Chengdu 611756,Sichuan,China)2(StateKeyLaboratoryforNovelSoftwareTechnology,NanjingUniversity,Nanjing210093,Jiangsu,China)
Aiming at the problems that current 3D skeleton extraction methods are highly complicated, the extraction results are not accurate enough, and few of them are specifically for human body models, we proposed a model segmentation-based 3D human body skeletons extraction method. First, we divided the model into parts according to the minimum geodesic distances between feature points of its vertices and ends. Secondly, we determined the topological hierarchies of each vertex of the model by the normalised geodesic distance function. Thirdly, based on model segmentation we extracted the original skeleton points according to their topological hierarchies. Finally, after some fine tuning, we connected all the skeleton points according to their topological relations and obtained a quite accurate human skeleton. Experimental results showed that the method reduces the complexity of the skeleton extraction algorithms effectively and gets more accurate extraction result for human body models with different postures.
Skeleton extractionModel segmentationGeodesic distanceTopological hierarchy
2015-04-02。国家自然科学基金面上项目(61371165);计算机软件新技术国家重点实验室开放课题基金项目(KFKT2013B22);浙江大学CAD&CG国家重点验室开放课题(A1416)。甘凌云,硕士,主研领域:虚拟现实。侯进,副教授。
TP391.9
A
10.3969/j.issn.1000-386x.2016.09.008

