一种支持混合QoS属性的服务选择方法

张丽芬　董才林　喻　莹　王艳红　贾静兰

(华中师范大学数学与统计学学院　湖北 武汉 430079)



一种支持混合QoS属性的服务选择方法

张丽芬董才林喻莹王艳红贾静兰

(华中师范大学数学与统计学学院湖北 武汉 430079)

当前的服务选择方法大都假设所有服务的QoS(Quality of Service)属性值必须均为确定的实数，并未考虑QoS属性的模糊性。这个假设在实际应用需求中具有一定的局限性，还会丢失大量的数据信息。为增强QoS表达能力，将QoS属性值描述成精确数值型、区间数值型、模糊数值型。同时，用序关系向量表示用户对不同QoS属性的需求偏好，将其转换成用户对QoS属性的主观权重，并采用熵权法计算QoS属性的客观权重。在此基础上，采用相对优势度算法给出混合QoS属性的服务选择过程。最后通过模拟和实验验证，证明相对优势度算法的有效性与合理性。

服务选择混合QoS相对优势度序关系向量熵权

0　引　言

随着互联网的快速发展，Web服务得以广泛运用，相关技术不断进步和发展。在Internet上涌现了大量的服务，为了选择最合适的服务，服务请求者通常首先搜索满足自身功能性需求的服务，发布在Internet上的多个服务(功能相似)都符合服务请求者功能性需求时，用户需要依据服务的非功能性属性尤其是服务质量QoS来进行服务选择。

从公开文献中可以发现，支持QoS的服务选择方法有基于QoS语义[1,2]的和基于QoS属性[3,4]的两种。以QoS语义为基础的服务选择方法是基于语义级的，它的基础是本体论，即QoS属性的描述采用QoS本体的方式，QoS的匹配依据QoS本体中的相似度。王伟锋等提出一种基于QoS的语义Web服务选择框架[1]，该框架不但可以提高QoS的语义描述能力，还能有效实现对服务的动态发现和选择。Tian等设计一种称为WS-QoS的方法对服务进行动态选择[2]，并构造出一个基于QoS语义的服务信誉框架和概念模型。以QoS属性为基础的服务选择方法是通过计算服务的各个QoS属性值，获得各个服务的QoS度量值，依据所定义的评价标准，对服务进行排序以实现服务的选择与评估[5]， 该方法是当今研究服务选择问题中较为流行的方法。王飞等借助模糊数学理论来描述服务的QoS属性，在此基础上，给出服务的评价与决策过程[3]，以便服务请求者选择合适的服务。李蜀瑜等通过比较两个服务的QoS属性的欧氏距离[4]，以此对两者的匹配度进行度量。

然而，目前基于QoS的服务选择方法中大都假设QoS属性的取值为一个确定的实数，未考虑QoS属性的模糊性。事实上，由于QoS属性的多样性以及服务资源调度的灵活性，使得服务提供者很难公布QoS属性的精确信息[6]，用精确实数表示服务的各个QoS属性值具有一定的不合理性。 为了有效解决这个问题，本文使用精确数值型、区间数值型、三角模糊数值型对QoS属性值分别进行描述，在此基础上，采用相对优势度算法给出混合型QoS属性的服务选择过程。

1　QoS属性描述

为了对比功能相似服务质量却不同的服务，需要构建服务的QoS属性模型。服务的质量信息可以采用不同的QoS属性进行描述，本文通过费用、可用性、响应时间、可靠性和声誉等5个属性来建立QoS属性模型：

1) 费用(Price)：费用是服务请求者调用服务时必须支付的货币量，在短期内基本不会发生变化，该值可用精确数值型表示。

2) 可用性(Availability)：可用性是服务在给定的一段时间内可访问的概率，因此将其表示为一个介于[0,1]区间的精确实数。

3) 响应时间(Time)：响应时间表示从服务请求者发出调用申请到最终获取服务执行结果所需时间。由于网络环境的动态性以及用户请求数的变化，响应时间T具有一定的波动特性，因此本文将响应时间T表示成一个区间型数值。

4) 可靠性(Reliability)：可靠性是衡量服务整体性能的指标量；其属性值来源于用户在调用服务过程中，对该服务的性能指标所作出的主观反馈。对于一个普通用户来说，通常都会以极高、很高、高、较高、一般、较低、低、很低、极低等语言型数值来表达可靠性。虽然语言型的数据具有合理的描述能力，但是无法直接参与QoS的度量计算，因此本文采用三角模糊数型对其量化。Re=(al,am,au) ，其中al,am,au分别表示三角模糊数的下界、核和上界值。三角模糊数的取值一般由领域专家(QoS专家和用户专家)给出[7]。

5) 声誉(Reputation)：声誉是衡量服务可信赖性的QoS属性，它主要依赖客户使用该服务的经历，由客户反馈得到，但是由于一些恶意打击，客户主观的声誉值缺少一定的可信性。因此，本文采用文献[8]给出的Web声誉模型WSrep，声誉值可由该模型自动生成。

2　主观权重的序关系向量表示

由于服务存在多个QoS属性，因此，当用户面临多个QoS需求间进行比较决策时，需要考虑用户对不同QoS属性的需求偏好[9]。用户利用排序的方式来表示对不同QoS属性的重视程度，从而可得各个QoS属性相对重要程度，更能体现一般用户的偏好需求[10]，弥补了精确权重表示的不足。设偏好次序为o=(o1,o2,…,oi,…,om)T，oi∈[1,m]表示用户对服务QoS属性ai的偏好次序，且oi值越小，用户的偏好程度越大。令vi=(m-oi)/(m-1)，vi为用户对QoS需求偏好的序关系向量，显然，vi值越大，用户的偏好程度越大，wis也越大。

对于用户给出的序关系型权重信息vi，最终的权重值应该尽可能地与它贴近，以此确保属性的主观权重wis能够充分反映用户对QoS属性的偏好，即主观权重wis尽可能地贴近vi。将某候选服务第i个属性与第j个属性间的序关系型权重信息的贴近度定义为：

那么候选服务所有m个QoS属性的序关系型权重信息的总贴近度和为：

为了获得各QoS属性最优的主观权重，需要保证总贴近度值最小，据此可构造如下最优化模型：

(1)

3　客观权重的熵权型表示

为了能让QoS属性的度量结果确切地体现服务的整体性能，以避免服务选择中用户偏好的局限性，本文提出客观权重的熵权法。熵权法[11]通过综合考虑各因素的信息量来计算一个综合指标，它主要依据各因素所反映的信息量大小来确定权重。熵权法可以贴切地反映服务各QoS属性的信息量，有效解释各QoS属性在QoS度量中的作用，它以服务QoS属性值的信息熵作为客观权重的确定依据。由此构造熵权模型以确定候选服务各QoS属性的客观权重，步骤如下：

设现有n个功能相似的候选服务WS={ws1,ws2,…,wsn}，对于每个候选服务都有以上的5个通用属性，其中，可用性、可靠性、声誉为正向属性(表现值越大越好的属性)，费用和响应时间为负向属性(表现值越大越劣的属性)。那么n个服务的QoS属性值可以构成一个矩阵A=[aij]n×5，aij表示第i个服务的第j个属性的QoS取值。

为了统一数据量纲，需要将决策矩阵A=[aij]n×5规范为标准化决策矩阵B=(bij)n×5。

步骤如表1所示。

表1　客观权重步骤示意

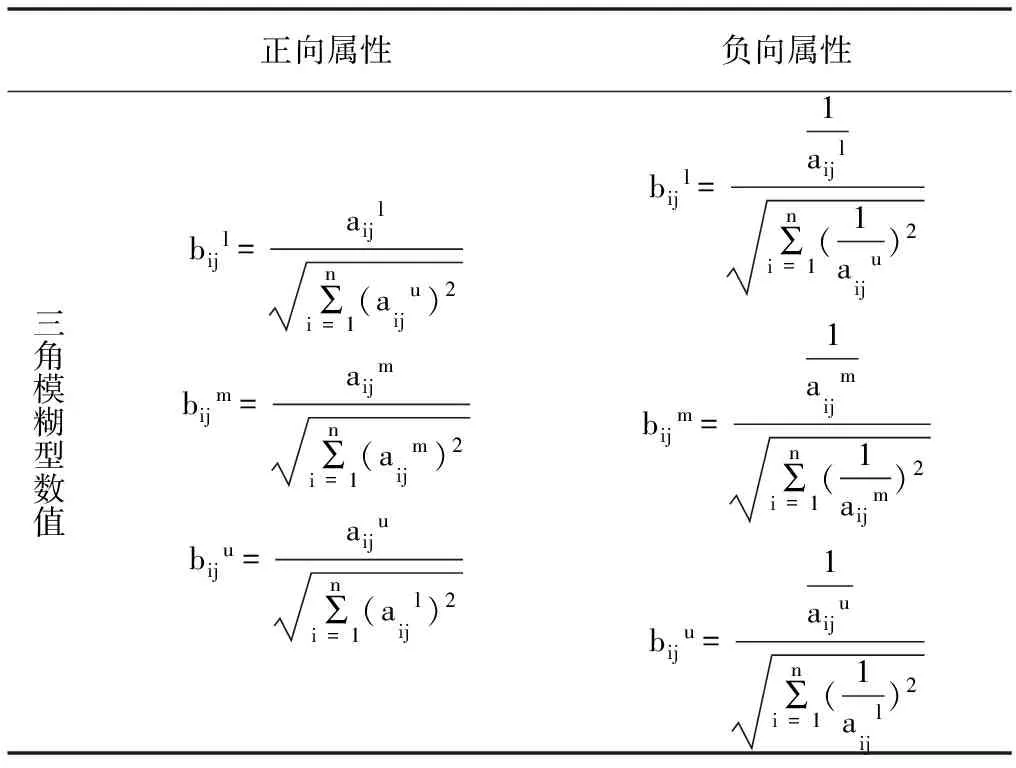
续表1

熵权的定义如下：

定义1对于一个具有n个候选服务、m个属性的多属性决策问题，属性j(1≤j≤m)的熵定义为:

(2)

定义2目前对于区间数值型、三角模糊数值型的客观赋权方法主要有区间数指标熵值法，它通过对各端点值求平均值，将区间型和三角模糊数型数值转化为实数型数值。然后利用平均值的信息熵来反映，但是这种方法显然不能充分反映各端点值间的偏差程度，存在一定的不足。在这里，本文综合利用各端点值输出的信息熵，以其平均值Ej来反映[12]:

(3)

(4)

将主观权重和客观权重相结合，可得到各属性的综合权重：wj=αwjs+(1-α)wjo，j=1,2,…,m，其中α∈[0,1]值可根据用户主观偏好的重要性而定。该系数表示服务选择中对用户偏好的依赖程度，即基于QoS的服务选择结果中主观与客观的比值，若忽略用户偏好，α取0；若服务选择完全依赖用户偏好，α取1。其值可依据用户主观偏好的重要性而定。显然，当α越大，主观权重对于综合权重的影响也就越明显。

4　基于相对优势度算法的服务排序

现有的针对混合QoS属性的服务选择问题的解决方法主要有两种：一种是先将混合的属性信息进行一致化，然后进行排序度量。所谓一致化就是将混合的属性信息转换成同一种数据类型，在这个过程中会造成混合属性信息的丢失，最后的决策结果很难具有较高的精确性。另一类则是利用扩展TOPSIS算法(technique for order preference by similarity to a ideal solution)，依据不同类型数据之间的距离[13]，计算每个评价对象和正、负理想解之间的距离，依据得到的距离对评价对象进行排序。该算法需要先对不同类型的数据进行归一化，其次找出正负理想解(并非实际存在)。另外，计算每个服务在各个属性上与正负理想解的欧式距离，计算过程较为复杂。

为了有效解决现有方法的不足，本文采用相对优势度算法解决服务选择问题。相对优势是国际贸易学的重要理论，它的原理是指一个生产者提供相同的服务或生产相同的商品时成本优于另一个生产者。因而，相对优势原理借用到服务选择过程中，就可以理解成在服务提供者提供的众多功能相同的候选服务集中，比较各个服务的服务质量，从中筛选出服务质量(QoS)相对最具优势的服务，即优势度最高的服务。

根据服务QoS属性之间可以相互补偿的特点，建立基于相对优势度的排序方法[14]。将总优势度值作为度量标准，对所有的候选服务进行排序后，就可以首先调用排序最优的服务，将其他服务视为备用服务。这样即使当排序最优的候选服务QoS下降甚至不可访问时，也能够及时调用备选服务，无需对候选服务进行再一次的排序计算。在该方法中，首先计算每个服务在每个属性上相对于其他服务的优势度,然后进行集结，最后得出每个服务相对于其他所有服务的总优势度，依总优势度值进行排序。该方法不需进行数据类型的转换，不必找正负理想服务，在实际的候选服务之间直接进行优势度的计算，计算过程简单直接。基于相对优势度的Web服务排序如图1所示。

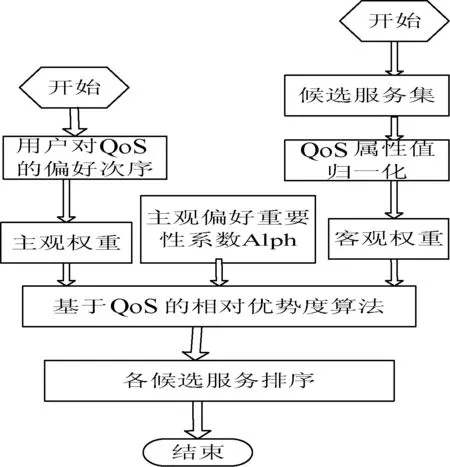
图1　基于相对优势度的Web服务排序

下面分别定义了精确数值型、区间数值型、三角模糊数值型中任意两个数据之间的相对优势。

定义3设a、b是两个实数，则a对于b的优势可以表示为：

s(a,b)=a-b

(5)

(6)

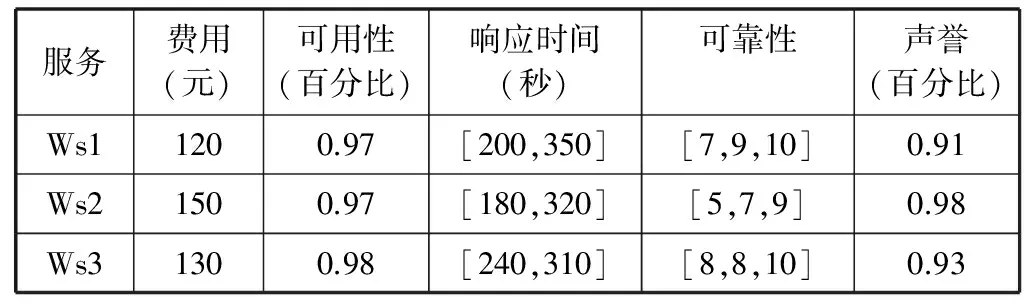
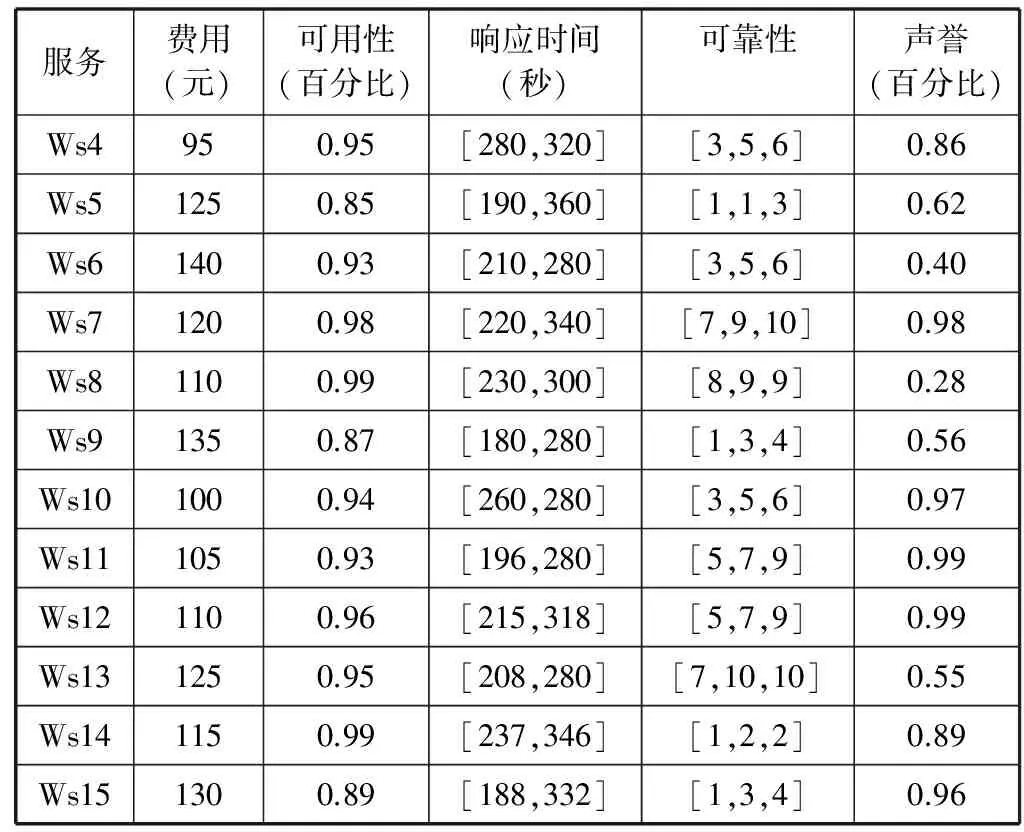
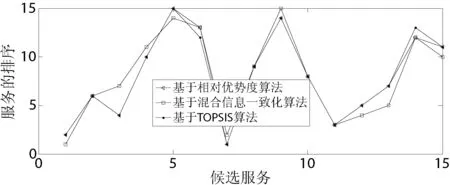
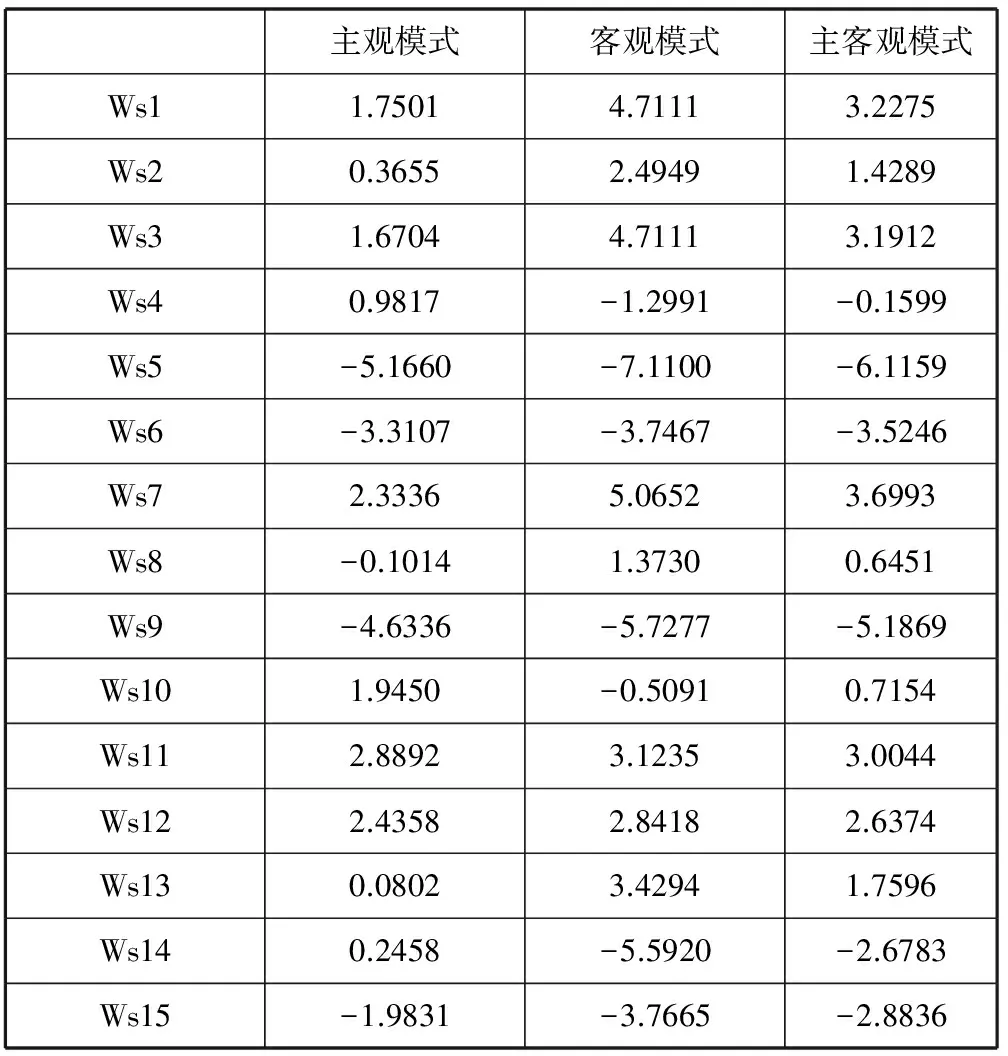
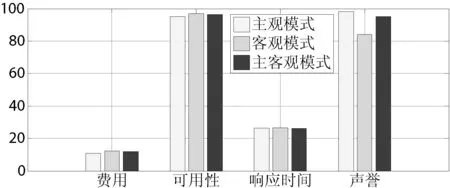
定义5设a=(al,am,au)、b=(bl,bm,bu)是两个三角模糊数，其中0

(7)

其中，la=au-al,lb=bu-bl。

相对优势度的排序方法:

第一步依据有限候选服务的各个属性值，计算服务wsi相对于服务wsj在每个属性at上的优势s(wsit,wsjt)=s(ait,ajt),i,j=1,2,…,n,i≠j；

当at属性值是实数时，s(ait,ajt)按式(5)计算；

当at属性值是区间时，s(ait,ajt)按式(6)计算；

当at属性值是三角模糊数时，s(ait,ajt)按式(7)计算。

第二步集结所有的s(wsit,wsjt)值，计算服务wsi相对于服务wsj在每个属性at上的优势度Dt(wsit,wsjt)；

若at是正向属性,则

Dt(wsit,wsjt)=s(wsit,wsjt)/maxst

(8)

若at是负向属性,则

Dt(wsit,wsjt)=-s(wsit,wsjt)/maxst

(9)

第三步计算服务wsi相对于服务wsj在所有属性上的优势度：

(10)

其中，wt是属性at的综合权重。

第四步计算每个服务wsi相对于其他所有服务的总优势度：

(11)

第五步根据D(wsi)排序。D(wsi)越大，说明服务wsi相对于其他服务的总优势度值越大，该服务排序越靠前。

5　实例及实验

基于文献[8]提供的混合QoS数据，候选服务QoS随机生成范围如下：价格在100～150之间；可用性在0.80～0.99之间；响应时间上界在180～280之间，下界在280～360之间；可靠性随机选取的语言短语集合{极高，很高，高，较高，一般，较低，低，很低，极低}，对应的三角模糊数见可靠性描述；声誉值按照模型自动生成，表2给出了QoS属性集合。本文以随机生成的混合QoS属性数据值为基础，引入主观权重与客观权重综合所得权重，按照相对优势度方法对服务排序，采用Matlab 7.0模仿服务选择。

表2　候选服务的QoS属性值

续表2

1) 为了验证本文算法的可行性，分别利用本文相对优势度算法、混合信息一致化算法(通过求区间型和三角模糊型数值各端点值的平均数，将混合的属性信息转换成精确实数)和文献[13]中的TOPSIS算法对下列15个候选服务排序。文献[13]中，为了计算简便，直接设各QoS属性权重均为0.2。为了能在相同的属性权重情况下，比较三种算法的最终排序结果，因而也先假设各属性权重为0.2。基于相对优势度算法、混合信息一致化算法和TOPSIS算法的服务排序结果如图2所示。

图2　三种算法的排序结果

可以看出，基于相对优势度算法与基于TOPSIS算法的排序结果基本相同，基于混合信息一致化算法排序结果却有较明显的差异。基于混合信息一致化算法所获取的最优服务是ws1，而利用本文的相对优势度算法与TOPSIS算法获取的最优服务均是ws7。由表2知，服务ws7与服务ws1相比，尽管服务ws1响应时间的最小值优于ws7，但它们在费用、可靠性这两个属性上取值相同，且ws7在可用性与声誉属性上的QoS值均明显优于ws1。因此，ws7明显优于ws1， 从而说明本文相对优势度算法不仅可行且有效，而混合信息一致化算法精确性不高。

2) 不同算法执行效率的对比。由图3可以看到，随着候选服务数目的增加，两种算法的平均运行时间呈递增形式，这是符合实际情况的。另外，基于相对优势度算法的执行效率要优于基于TOPSIS算法的执行效率，因为TOPSIS算法要对属性矩阵进行归一化，而且需计算较复杂的欧氏距离，在运行时间上明显大于相对优势度算法。

图3　两种算法运行效率的对比

3) 分析基于需求偏好的不同赋权模式的服务选择。当α=0时，即在计算QoS属性权重时，完全依赖于用户对QoS的需求偏好，称其为需求偏好的主观赋权模式；当α=1时，即在计算QoS属性权重时，忽略用户的需求偏好，仅考虑QoS属性值客观数据，称其为需求偏好的客观赋权模式；当α=0.5时，即在计算QoS属性权重时，既考虑用户的需求偏好又考虑QoS属性值，称为需求偏好的主客观赋权模式。候选服务的总优势度如表3所示。

表3　候选服务的总优势度

选取排序前四的4个候选服务，计算它们在各个QoS属性上的均值(在计算响应时间时，取区间左右两端值的平均值)。为了能在一个图中直观显示与比较基于不同赋权模式的服务选择的排序结果，将可用性、声誉的属性值放大100 倍，费用和响应时间的属性值缩小10 倍，如图4所示。

图4　不同赋权模式的服务选择结果对比

由图4可知，主观赋权模式分别在费用、声誉达到最大，但可用性偏低，响应时间偏高，用户偏好使得服务QoS属性信息的实际效用不一致；客观赋权模式在可用性、响应时间达到最优，但声誉、费用不是最佳；而主客观赋权模式在各个QoS属性信息上表现了很好的中间性， 既能表达用户偏好又能反映服务QoS的客观特征，显示出更强的灵活特性。

6　结　语

在开放的Internet环境中，描述服务QoS属性的方式具有多样性。本文使用精确数值型、区间数值型、三角模糊数值型对QoS属性值分别进行描述，利用序关系向量表示用户的主观偏好，同时利用熵权表示QoS属性的客观权重。在此基础上，采用相对优势度算法给出混合型QoS属性的服务选择过程。

通过模拟仿真和实验验证，相对优势度算法能够有效地对功能相似的服务优劣作出选择，筛选出既能满足用户QoS需求偏好又具有较优质量的服务；并且该算法与现有算法相比具有较高的执行效率。本文采用需求偏好的主客观赋权模式在各个QoS属性值上能够表现出很好的中间性，进一步证明了主客观赋权模式的合理性。如何把相对优势度算法用于大批量的混合型QoS属性的服务选择是下一步需要研究的问题。

[1] 王伟锋,刘亚军.基于QoS的语义Web服务选择框架[J]. 计算机与数字工程,2009,37(9):15-19.

[2] Tian M,Gramm A,Ritter H, et al.Efficient selection and monitoring of QoS-aware web services with the WS-QoS framework[C]//Proceedings of the IEEE/WIC/ACM International Conference on Web Intelligence,Beijing,China,2004:152-158.

[3] 王飞,邹仕洪,陈山枝，等. 基于模糊数学的Web服务QoS建模[J]. 计算机应用研究,2007,24(4):214-216.

[4] 李蜀瑜,周娟. 基于WSMO服务质量的语义Web服务发现框架[J]. 计算机应用,2009,29(8):2299-2302.

[5] 王胜利.数据挖掘技术在Web服务分类中的应用研究[D].广东：暨南大学,2010.

[6] 马玉倩,付晓东, 代志华，等.一种混合QoS 感知的Web 服务选择方法[J]. 计算机应用与软件,2012,29(6):39-42.

[7] Klir G J, Yuan B. Fuzzy Sets and Fuzzy Logic: Theory and Applications[M].New Jersey: Prentice Hall PTR, 1995.

[8] 杨放春, 苏森, 李祯. 混合QoS模型感知的语义 Web 服务组合策略[J].中国科学E辑：信息科学, 2008, 38(10):1697-1716.

[9] 马友,王尚广,孙其博，等.一种综合考虑主客观权重的 Web 服务QoS度量算法[J].软件学报, 2014,25(11):2473-2485.

[10] 辛乐,范玉顺,李想,等.基于服务信誉评价的偏好分析与推荐模型[J].计算机集成制造系统，2014,20(12):3170-3181.

[11] 程冬,董才林,喻莹.一种基于模糊理论的Web服务信任评估模型[J].计算机应用与软件，2012,29(10):82-84，179.

[12] 郭秀英.区间数指标权重确定的熵值法改进[J].统计与决策，2012(17):32-34.

[13] 李小林,张力娜. 基于混合QoS模型的服务选择策略[J].科学技术与工程，2012,12(22):5653-5657，5660.

[14] Qian Y H, Liang J Y,Song P,et al. On dominance relations in disjunctive set-valued ordered information systems[J].International Journal of Information Technology and Decision Making,2010,9(1):9-33.

A WEB SERVICE SELECTION METHOD SUPPORTING HYBRID QOS ATTRIBUTES

Zhang LifenDong CailinYu YingWang YanhongJia Jinglan

(School of Mathematics and Statistics, Huazhong Normal University, Wuhan 430079,Hubei,China)

Current Web service selection methods mostly assume that all the QoS attribute values of Web services have to be the definite real numbers; but do not take into account the fuzziness property of QoS. This hypothesis has certain limitation in practical application requirement; what’s more, it will also cause the loss of a large amount of data information. To enhance the representation capability of QoS, we described the QoS attributes as the accurate numerical type, the interval numerical type and the fuzzy numerical type. At the same time, we used the order relations vector to represent the demand preference of user on different QoS attributes and converted them into user’s subjective weights on QoS attributes, as well as calculated the objective weights of QoS attributes with entropy weight. On this basis, we gave Web service selection process of hybrid QoS attributes by using relative superiority degree algorithm. At last we proved the effectiveness and rationality of the relative superiority degree algorithm through simulation and experiment verification.

Web service selectionHybrid QoSRelative superiority degreeOrder relation vectorEntropy weight

2015-04-20。张丽芬，硕士生，主研领域：Web服务。董才林，教授。喻莹，副教授。王艳红，硕士生。贾静兰，硕士生。

TP3

A

10.3969/j.issn.1000-386x.2016.09.004