超长巷道炮掘时粉尘分布规律研究

贺光会

(山西晋城煤业集团寺河矿)



超长巷道炮掘时粉尘分布规律研究

贺光会

(山西晋城煤业集团寺河矿)

为确定长距离爆破掘进工作面粉尘运移规律，以指导防尘系统设计，依托某矿1100掘进工作面，建立1∶1几何模型进行CFD模拟，测算空气流场和粉尘运动边界条件。根据湍流模型适用性和空气流场分布特征，优选RNGk-ε湍流模型模拟1100掘进工作面空气流场，算得空间内粉尘体积分数小于10 %，因此选用离散相模型模拟爆破空间粉尘非稳态运动。最终获得距掘进面60 m范围内粉尘扩散、粒径沉降和浓度时间变化规律：粉尘浓度沿垂向分布有明显分界，浓度随垂高在0.5～4 m递增而降低，粉尘浓度沿纵向先升高而后降低；粒径为10 μm以下粉尘均匀分布于空间，沉降量沿纵向呈“减少—增高—减少—增高”趋势，10～200 μm粉尘则呈“减少—增高—减少”趋势，15～200 μm粉尘几乎完全沉降；爆破后5 min内粉尘浓度急剧下降，5～50 min粉尘浓度下降缓慢，高浓度区长时间停留在距工作面40 m之内，不沿巷道运移；距工作面10～20 m形成的空气涡流区是影响粉尘扩散、沉降和浓度变化的重要因素。爆破期间在距工作面20，25 m处，分别采用AKFC-92A采样器和CCHZ-1000全自动粉尘测量仪监测粉尘浓度，实测值与模拟值基本相符，模拟结果可靠。

长距离掘进 爆破 粉尘运移 数值模拟

矿山开拓中爆破掘进是主要手段之一。爆破作业时产生的粉尘是井下作业的主要尘毒来源，粉尘长时间滞留在空气中，严重污染作业环境。特别是在工作面附近的一段巷道，爆破瞬间产生的大量粉尘在风筒射流作用下运动状态相当复杂。为有针对性的采取防尘措施，改造通风系统，改善作业环境，有必要了解这一过程粉尘颗粒扩散、粉尘粒径沉降和粉尘浓度的时间变化规律。

目前对爆破过程中粉尘运动规律的研究主要有廖贤鑫、蒋仲安[1-3]，李锋等[4]利用fluent分析了采场爆破后粉尘及有害气体的扩散行为。郑炳旭等[5]提出了利用正态分布无边界式粉尘扩散模式预测粉尘浓度的方法，可对爆破过程粉尘的扩散进行数值预测，并给出了爆破产尘量及爆破产生烟云体积的计算方法。许秦坤等[6]认为爆破产尘粒度、产尘浓度与爆破对象和爆破工艺有关。王继峰[7]给出了爆破空间千克炸药需风量的计算方法。李怀宇[8]分析了露天矿爆破初期粒子行为，基于“粒子法”建立了粉尘运动的数学模型，对爆破粉尘的初期运动行为进行了模拟计算。孙佳等[9]针对露天爆破粉尘的运动行为，提出了粒子系统概念，将爆破产尘过程分为3个时期，针对各个时期粉尘行为特点建立了相应模型算法，并进行了实时模拟。以上对爆破产尘运移规律的研究多是针对采场和处于自由空间的露天矿山，且没有考虑粒子的空间分布状态。本文将基于有限空间的掘进作业面，系统、全面模拟分析爆破产尘浓度扩散及浓度时间变化规律，同时分析不同粒径粉尘的空间分布及沉降状态，能够更好地反映出爆破过程粉尘的运移规律，为防尘系统设计提供参考。

1 巷道布局及通风情况

该矿区中1100斜坡道的巷道布置如图1所示，巷道掘进方式为岩巷爆破掘进，局部通风系统采用2×37 kW的局部通风机送风，其中一台向工作面送风，另一台向邻近硐室送风，供风参数如表1。

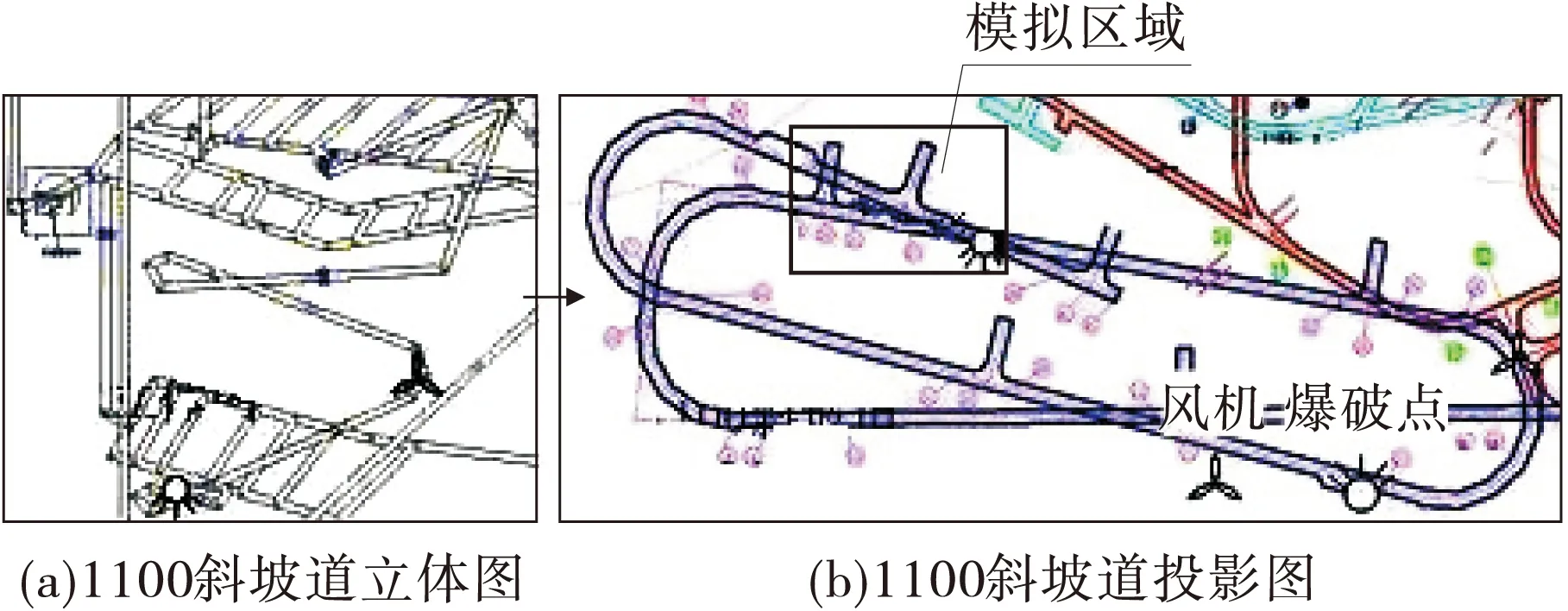
图1 1100斜坡道巷道布置

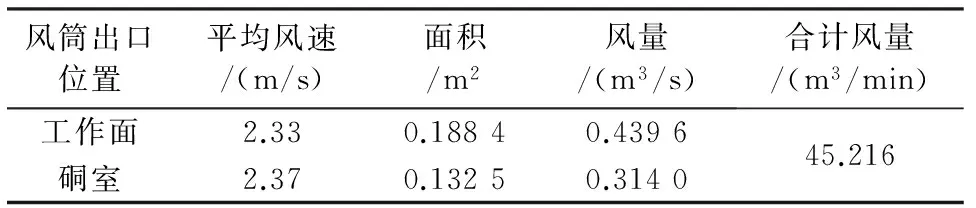
风筒出口位置平均风速/(m/s)面积/m2风量/(m3/s)合计风量/(m3/min)工作面2.330.18840.4396硐室2.370.13250.314045.216

2 湍流模型选择与几何模型建立

2.1 湍流模型选择

结合1100斜坡道掘进工作面气流旋转运动的特点，综合考虑计算精度和求解效率因素，通过对比分析各种湍流模型的特点及适用性，决定采用RNGk-ε湍流模型对基本控制方程进行封闭，在标准k-ε湍流模型的基础上，增加ε方程约束。

通过修改湍流黏度，充分考虑了平均流动中的旋流及旋转流动，能更好地处理高应变率及轨迹弯曲较大的流动，输运方程[10]为

k方程

(1)

ε方程：

(2)

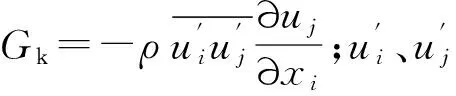
2.2 爆破参数计算与多相流模型选择

爆破空间的粒子运动属于多相流运动，目前针对多相流运动的模拟fluent中提出的数值模型主要有基于欧拉-拉格朗日法的DPM模型，以及基于欧拉-欧拉法的VOF模型、Mixture模型和Eulerian模型3种模型[11]。通常情况下，当粒子的体积分数超过10%时，宜用欧拉-欧拉法对粒子云状态进行追踪；当粒子的体积分数小于10%时，采用欧拉-拉格朗日法对粒子运动进行追踪。为了选择适当的多相流模型用于1100斜坡道爆破工作面粉尘运动状态数值模拟，对相关参数计算如下[5]。

2.2.1 爆破参数计算与多相流模型确定

(1)爆破烟云量计算。

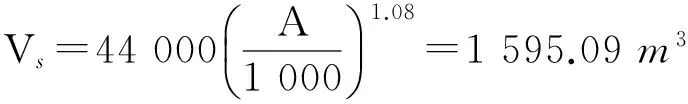
(3)

式中，A为周边构件爆破的炸药量，将掏槽眼、辅助眼、周边眼以及底眼所用炸药量累计,得到本次爆破所用炸药量为46.35 kg；Vs为爆破开岩生成的烟云量，m3。

(2)单位体积结构物产生的粉尘量。

qb=149(ak1)2k2=241.84g/m3，

(4)

式中，a为结构物单位炸药消耗量，取3次爆破平均值1.30 kg/m3；k1、k2分别为结构物炸药能量利用系数、材料产尘系数，对于地下岩体，k1、k2分别取0.98，1.0。

(3)根据本次爆破炸药消耗量和结构物单位炸药消耗量,确定爆破结构体积为

(5)

(4)爆破直接破碎建筑物粉尘

Qb=qbvb=8 621.60g.

(6)

(5)爆破初期尘源粉尘浓度

(7)

(6)粉尘粒子的初始速度

(8)

式中，S为断面积，取20.66 m2；τ为粉尘喷射时间，取2 s。

(7)粉尘质量流率计算

Qm=cvS=4.314kg/s.

(9)

(8)炮烟流量

Qy=Sv=797.48m3/s.

(10)

(9)粉尘流量

Qc=Qm/ρc=0.001 598m3/s,

(11)

式中，ρc为爆破岩体密度，kg/m3。

(10)爆破产生粉尘体积分数

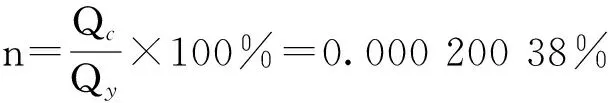
(12)

可见，爆破产生粉尘的体积分数小于10%，故应采用DPM模型进行计算。

2.2.2 颗粒运动方程

对于粉尘颗粒通过积分作用力微分方程得出运动轨道，由于运动过程中视质量力、升力及热泳力相对于重力和曳力数量级较小，可忽略不计。因此在笛卡尔坐标系下，颗粒作用力平衡方程[12]为

(13)

(14)

式中，u为气流速度，m/s；up为颗粒运动速度，m/s；gx为重力加速度，m/s2；ρp为颗粒密度，kg/m3；FD(u-up)为颗粒的单位质量曳力;CD为曳力系数；dp为颗粒直径，m。

通过确定气流的瞬时速度来跟踪颗粒的随机轨道，可以考虑颗粒的湍流扩散，颗粒轨道控制方程为

(15)

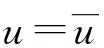
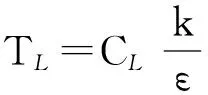
2.3 几何模型建立

在对巷道沿程风速测定过程中发现，距工作面45 m之后巷道风速基本保持不变，且由于作业强度主要密集在工作面附近，因此选取60 m巷道进行CFD模拟分析即可满足需要。模型巷道尺寸为：宽5.1 m，高4.6 m，半圆拱形，坡度为8.1°。风筒距工作面距离21.8 m，由于到达风筒出口风量小，风筒口发生变形，直径近似为420 mm。风筒中心距右帮3 m，距底板4.3 m。在距工作面25 m处有一硐室，硐室长21 m，宽4.6 m，高4.4 m。硐室配有直径约490 mm风筒，风筒中心距右帮2.5 m，距底板4.3 m，据此建立几何模型(图2)，爆破作业面在X=0处。

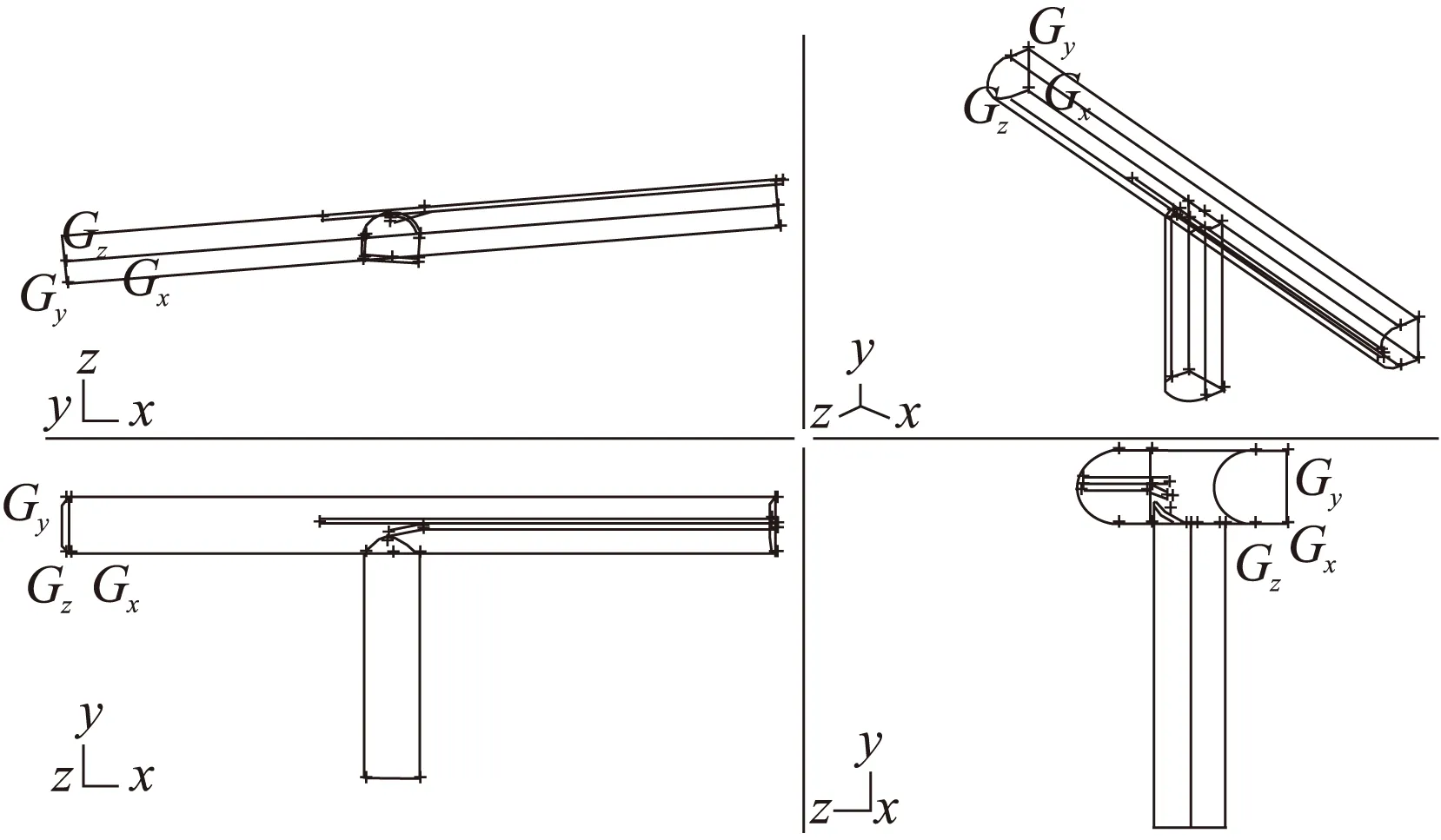
图2 1100斜坡道工作面几何模型

3 爆破粉尘运移CFD模拟分析

3.1 DPM模型条件指定

根据2.2得到的参数和2.3节建立的模型，结合1100斜坡道爆破工作面实际条件，对用于粉尘运动模拟的DPM模型条件设置如表2所示。

3.2 爆破粉尘扩散规律分析

为得到粉尘在巷道空间内垂直方向及纵向的扩

散情况，分别在爆破后第30和第50 min对巷道内的粉尘浓度分布情况进行模拟，得到粉尘浓度分布曲线如图3、图5所示，粉尘浓度分布云图如图4、图6所示。

从图3可以看出，随着垂直高度在0～0.5 m递增，粉尘浓度递减，且垂高为0.5 m处浓度最高，距地表4 m处浓度最低，垂直方向上不同高度处粉尘浓度有明显分界，这是因为大颗粒粉尘自重较大，不易随气流浮动，只在较低的水平内运动；而呼吸性粉尘受风流扰动作用强烈，均匀分布于空间中，因此巷道顶部粉尘浓度较低。如图4，沿巷道纵向60 m范围内，随着距离工作面加大，粉尘浓度先升高而后降低；粉尘浓度升高段距工作面10～20 m，属于风筒射流形成涡流控制区域，风流变化剧烈使得粉尘难以沉降，距离工作面40 m后粉尘浓度明显降低，并维持在较为均匀的水平。

从图5、图6可以看出，爆破50 min后粉尘在垂直方向分布、沿程分布与30 min基本一致，但整体浓度有所下降，这表明爆破掘进过程中，虽然空间内粉尘浓度随时间延长逐渐降低，巷道空间内粉尘浓度的扩散规律保持不变。对比图3和图5、图4和图6可知，爆破后30和50 min，距工作面10～20 m粉尘浓度始终为整个空间的最高区域，没有明显扩散趋势。

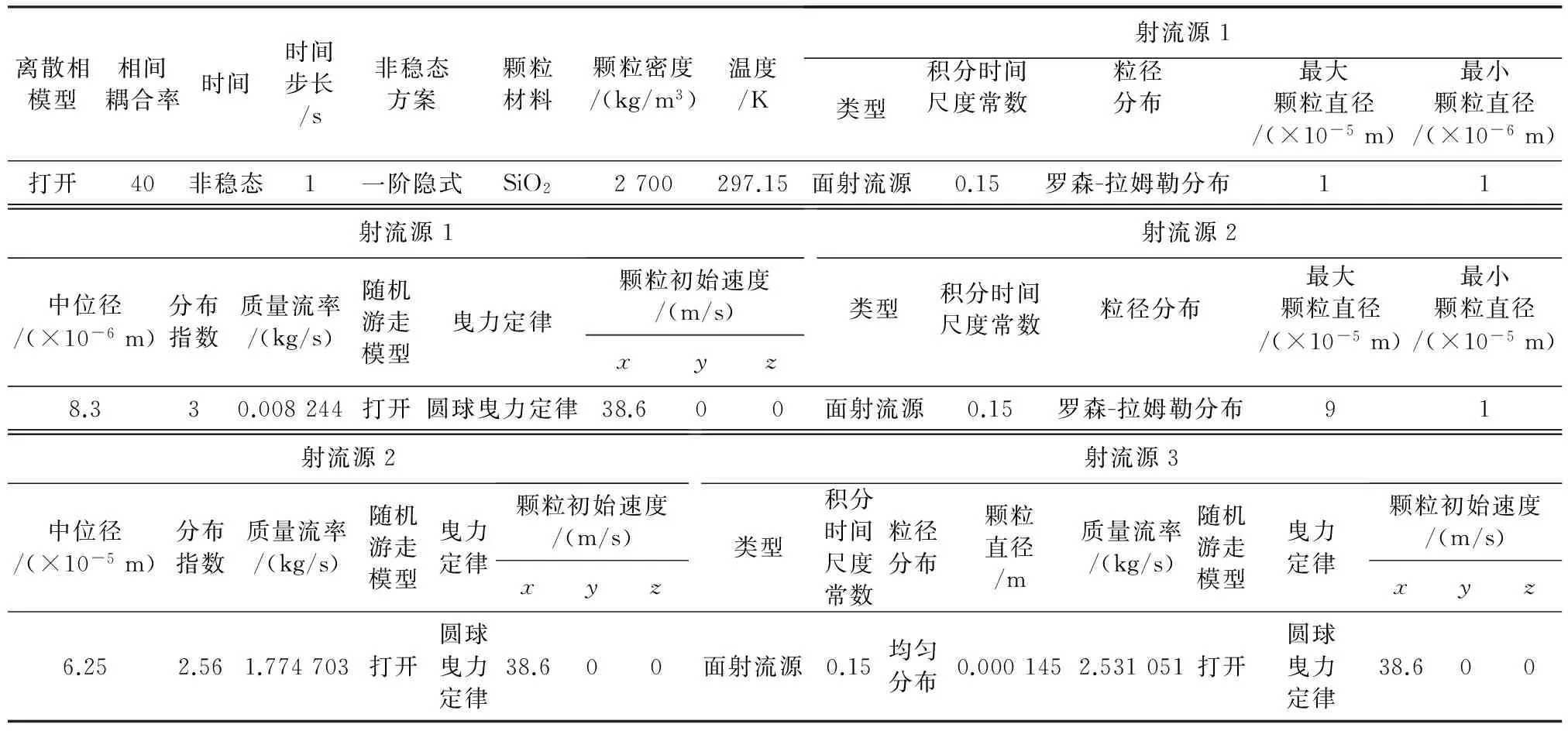
表2 离散相模型主要参数

3.3 爆破粉尘粒径沉降规律分析

以往在对粉尘沉降规律的模拟上，多以颗粒轨迹形式来表述颗粒沉降状态[11-12]，对于存在旋转涡流的流场，颗粒轨迹混乱，无法清楚的表述颗粒的空间分布和沉降状态。本文采用点颗粒的形式对粉尘的空间分布及沉降进行追踪，在爆破50 min后以颗粒形式显示不同粒径粉尘在空间的分布状态。由于前期试验发现粒径为90 μm以上粉尘沉降数量较少，因此将粒径为90～200 μm的颗粒用中间径145 μm来统一表示。经模拟得到颗粒空间分布状态如图7～图9所示。

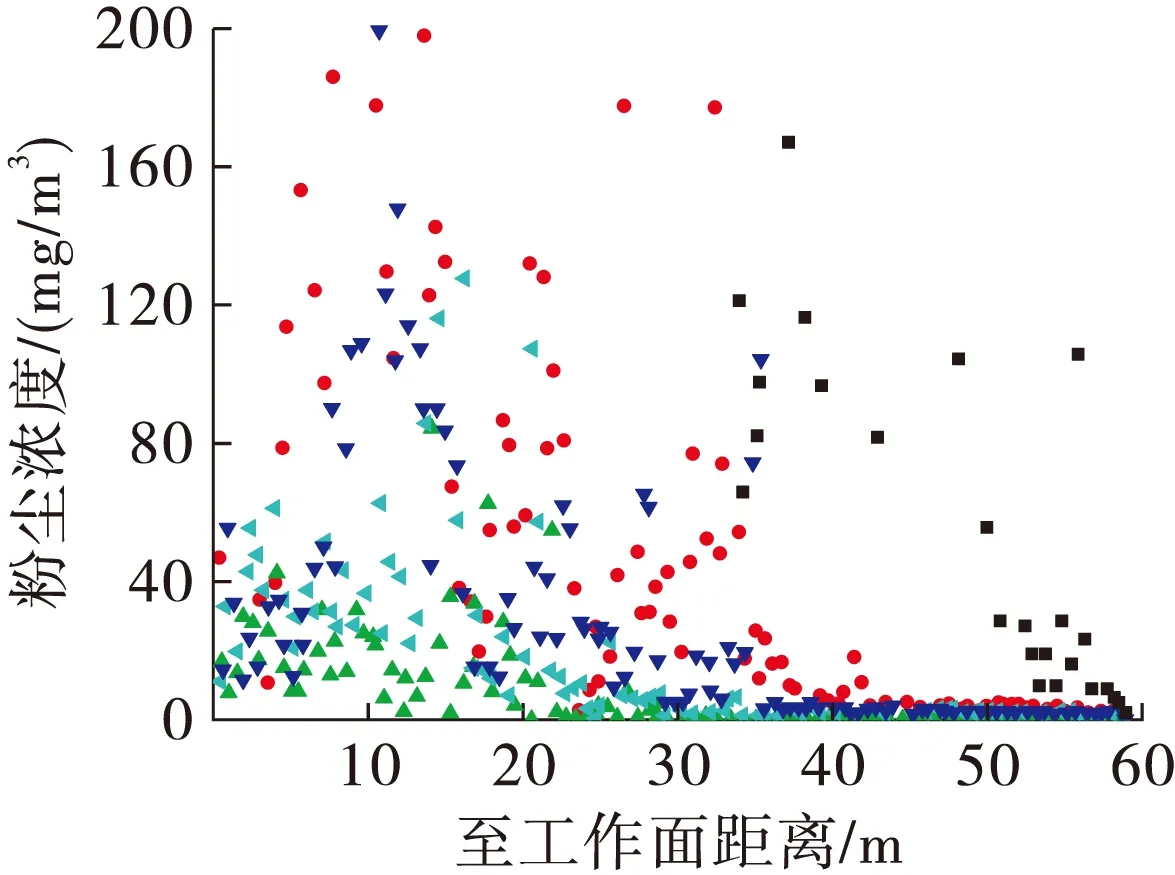
图3 30 min不同高度处粉尘浓度分布

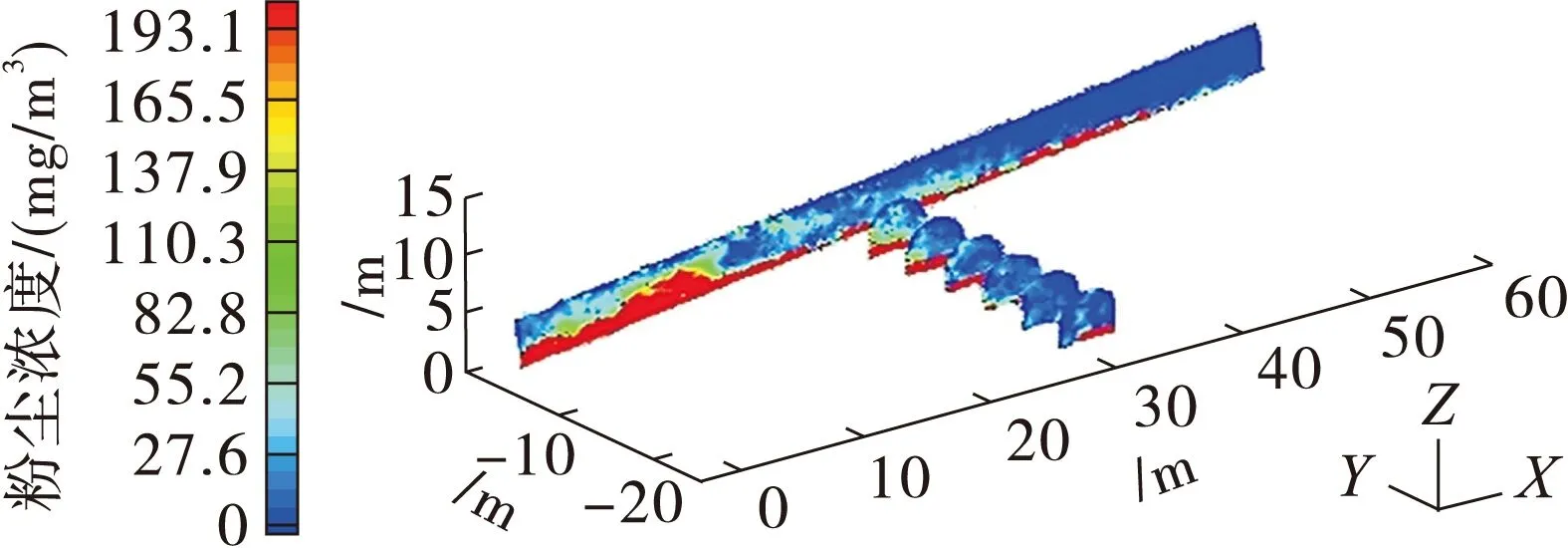
图4 30 min粉尘沿程浓度分布(X方向)

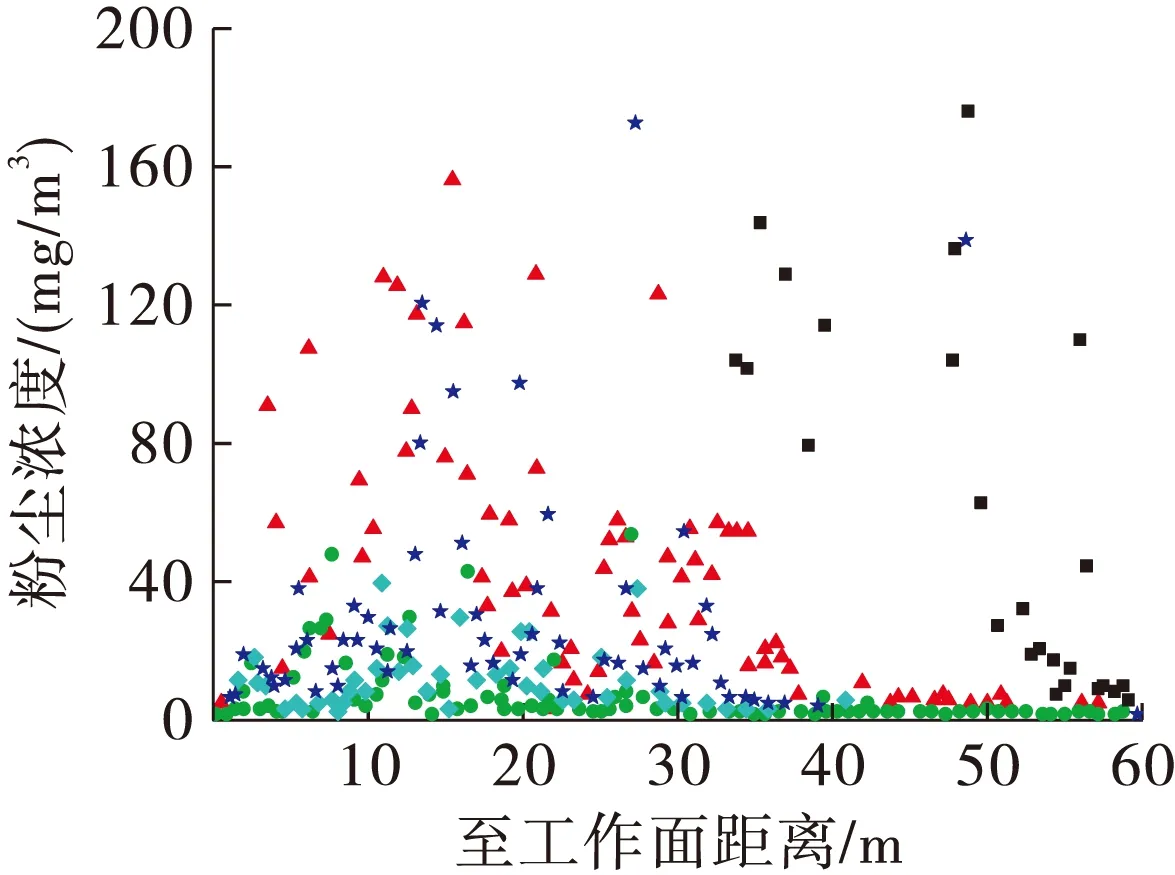
图5 50 min不同高度处粉尘浓度分布

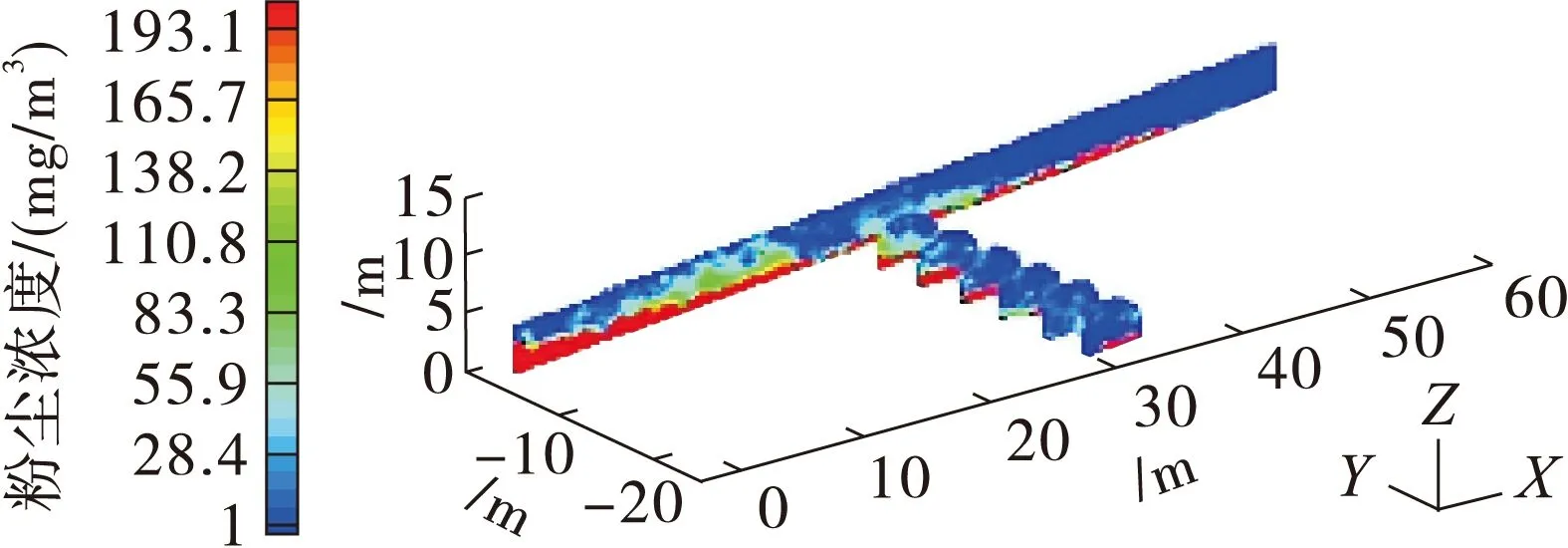
图6 50 min粉尘沿程浓度分布(X方向)

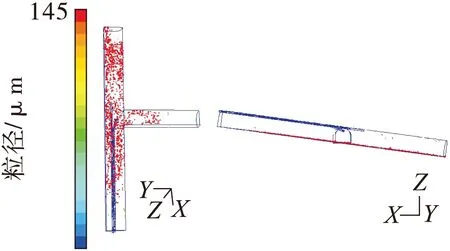
图7 粒径为145 μm (90～200 μm) 粉尘空间分布状态

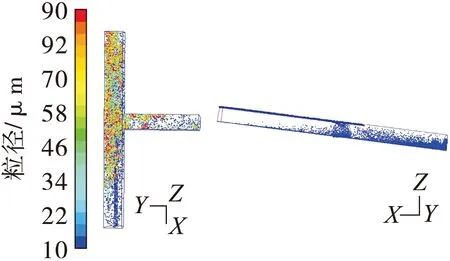
图8 粒径为10～90 μm粉尘空间分布状态

如图7，粒径为90～200 μm的粉尘没有在空间内浮动，几乎完全沉降，在风筒底部约距工作面10～20 m处沉降量相对较少。如图8，粒径为10～90 μm粉尘中粒径为15 μm以下的粉尘，长时间悬浮于距离工作面40 m以内空间(该段空气流场变化较为剧烈)，40 m以后则基本沉降；粒径在15 μm以上的粉尘几乎完全沉降。总体来看，在这一粒径区间的粉尘沉降量大于悬浮量。如图9，粒径在10 μm以下的粉尘均匀分布于沿程空间各点，沉降数量及空间分布数量均较多，可见小颗粒粉尘受气流干扰剧烈，易随空气飘动。这些微细粉尘大范围、长时间悬浮于空气中，且悬浮高度均达到了呼吸带高度，给人体造成巨大危害，因此应加强小颗粒粉尘抑制措施。

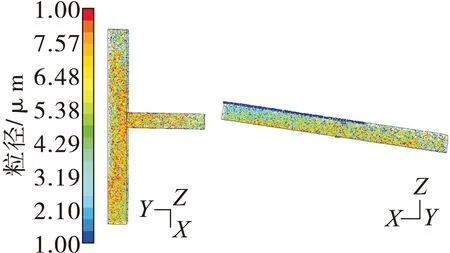
图9 粒径为10 μm以下粉尘空间分布状态

为了更清楚地分析颗粒的沉降状态，将空间内的粉尘粒径等级按<10 μm、10～30 μm、30～50 μm、50～70 μm、70～90 μm、90～200 μm(以145 μm代表)划分，并对距工作面60 m范围内不同等级颗粒的沉降数量进行统计。

如图10所示。距离工作面60 m范围内，粒径在10 μm以下的粉尘沿程沉降数量最多。沉降量总体在距工作面10 m以内，10～20 m，20～40 m，40 m 之后4个区间内对应呈“减少—增高—减少—增高”的趋势。对于粒径为10～30 μm，30～50 μm，50～70 μm，70～90 μm，90～200 μm的粉尘沉降量总体在距工作面20 m以内，20～25 m，25 m之后3个区间内对应呈“减少—增高—减少”的趋势，且在距工作面25 m以后，粉尘沉降量基本呈线性下降。在15～20 m段，10～200 μm粉尘沉降量较少，是因为该段正处于风筒射流形成的漩涡附近，涡流效应造成二次扬尘，使得漩涡附近粉尘沉降量减少。

3.4 爆破粉尘浓度时间变化规律分析

爆破过程粉尘的运动是一个非稳态过程，经模拟得出爆破后1～50 min的粉尘浓度变化如图11所示。从图11中可以看出，在爆破t=1 min后，距工作面60 m之内的掘进空间粉尘浓度较高，基本在200 mg/m3以上；40 m之后粉尘浓度相对较低，沿程巷道各点粉尘浓度随着距工作面距离增加呈逐渐下降的趋势。1～5 min粉尘浓度急剧下降，在距离工作面10～20 m空间粉尘浓度相对较高。

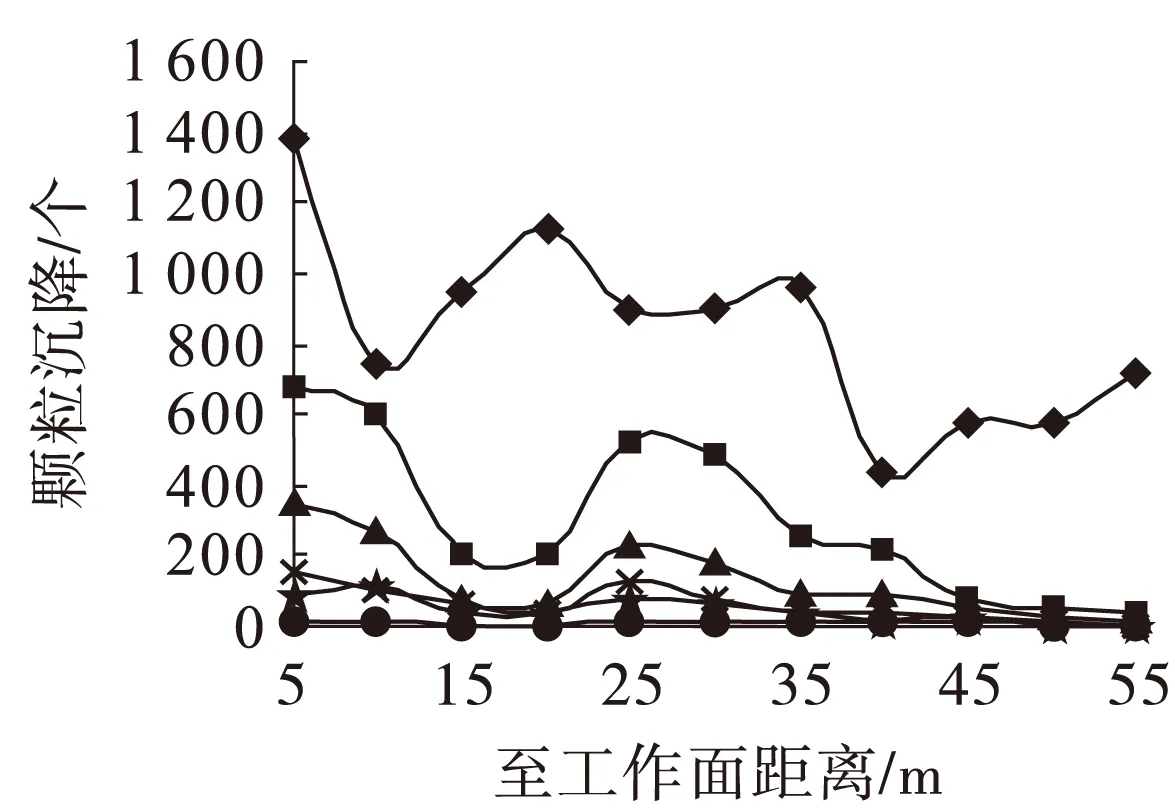
图10 不同粒径粉尘纵向沉降规律

爆破后5～50 min，巷道沿程粉尘浓度随时间延长降低趋势较爆破初期相对减弱，距离工作面40 m以后粉尘浓度长时间维持在相对较低的标准，明显低于距工作面40 m以内区域，并基本不再变化。巷道10～20 m粉尘浓度则仍维持在相对较高水平。

由此分析，爆破初期在瞬间抛射动力作用下，粉尘短时间充满整个掘进空间，使得初期粉尘浓度偏高。在1～5 min，大颗粒粉尘由于自重作用迅速沉降，使得这一时间段内粉尘浓度迅速降低。相反，小颗粒粉尘由于易随空气运动则长时间悬浮，因此5 min之后粉尘浓度呈缓慢下降的趋势。在爆破掘进粉尘浓度随时间变化的整个过程中，由于风筒出口附近形成了涡流卷吸控制区，使得粉尘运动紊乱、剧烈，不易沉降。在距工作面10～20 m粉尘浓度长时间维持在较高的标准。高浓度区域没有沿着巷道扩散运移的趋势，长时间停留在距 工作面40 m之内。可见，现有的通风条件下，在爆破之后较长时间内，粉尘浓度仍维持在较高水准，需通过提高作业面供风量或采用辅助降尘措施来控制粉尘。

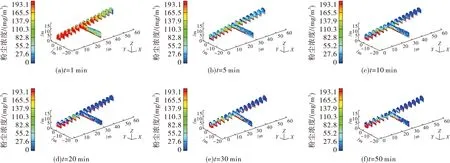
图11 粉尘浓度分布随时间变化

图12为距工作面20及25 m处粉尘浓度随时间变化的模拟结果，为了验证模拟结果的可靠性，在充分防护前提下距工作面20，25 m 处分别用AKFC-92A采样器、CCHZ-1000全自动粉尘测定仪测量粉尘浓度。放炮时间为11∶36，20 m处测点开始测量时间为11∶44，25 m处测点开始测量时间为11∶48，以后每隔若干时间测量一次，测量结果如表3所示。

由此可见，对于距工作面20 m及25 m处粉尘浓度的模拟结果与实测得到的粉尘浓度变化规律基本相符，可以认定数值模拟得出的结论可靠。

4 结 论

(1)粉尘扩散规律。粉尘浓度随地表垂高距离增高而降低，并有明显分界，距地表0.5 m处粉尘浓度最高， 4 m处粉尘浓度最低。沿巷道纵向，粉尘浓度先升高而后降低，升高段距工作面10～20 m，高浓度区域没有明显扩散趋势。

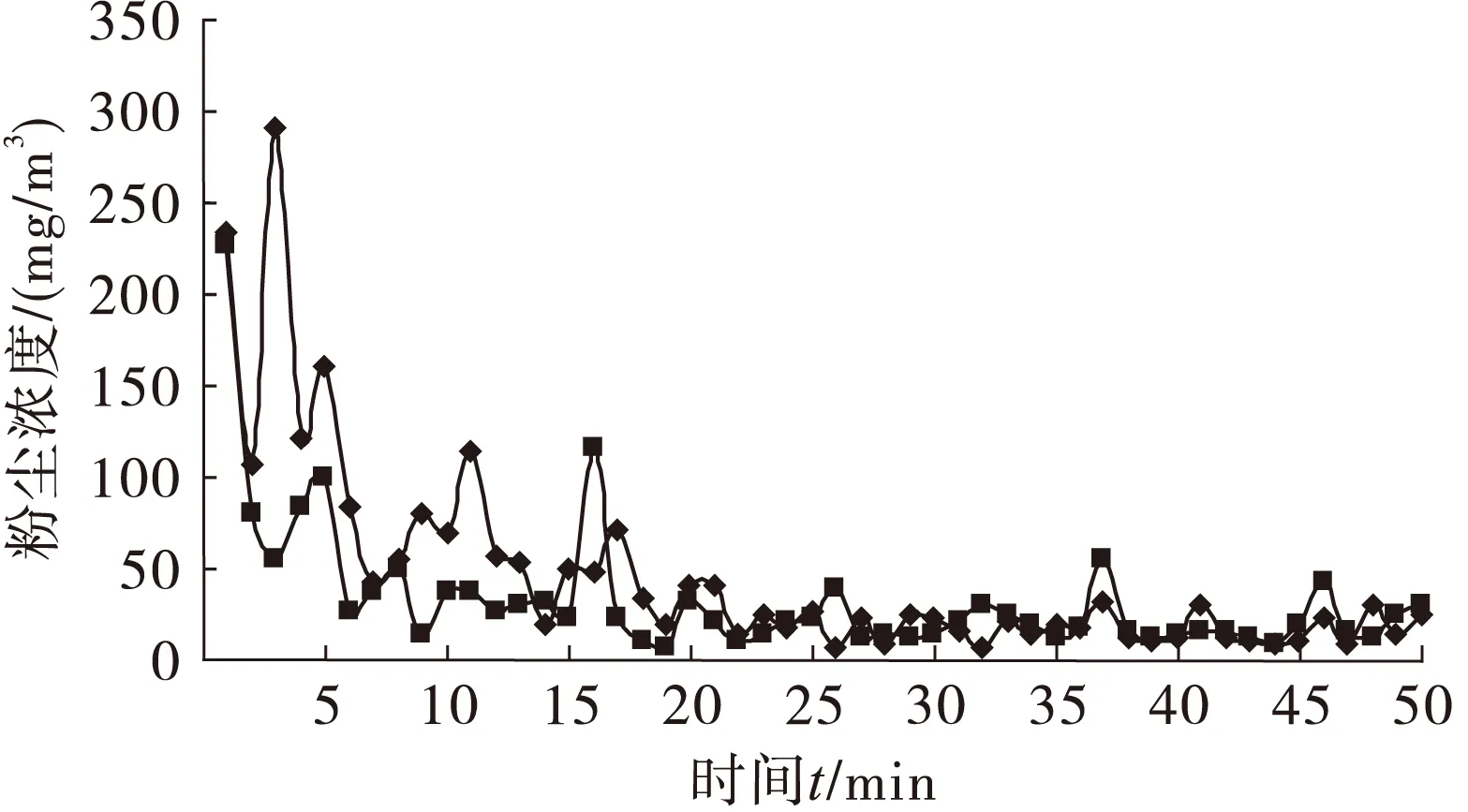
图12 20 m、25 m处粉尘浓度随时间变化

(2)粉尘粒径沉降规律。粒径为10 μm以下粉尘均匀分布于空间，沉降量沿纵向呈“减少—增高—减少—增高”趋势，10～200 μm粉尘则呈“减少—增高—减少”趋势，粒径为10～15 μm粉尘长时间悬浮于距离工作面40 m以内空间，40 m以后则基本沉降，15～200 μm粉尘几乎完全沉降。

(3)粉尘浓度时间变化规律。在爆破后1～5 min，大颗粒粉尘迅速沉降，使得粉尘浓度急剧下降，5 min之后粉尘浓度缓慢下降。距工作面10～20 m粉尘浓度长时间维持在较高的标准，在距工作面20，25 m处粉尘浓度的模拟结果与实测变化规律基本相符。

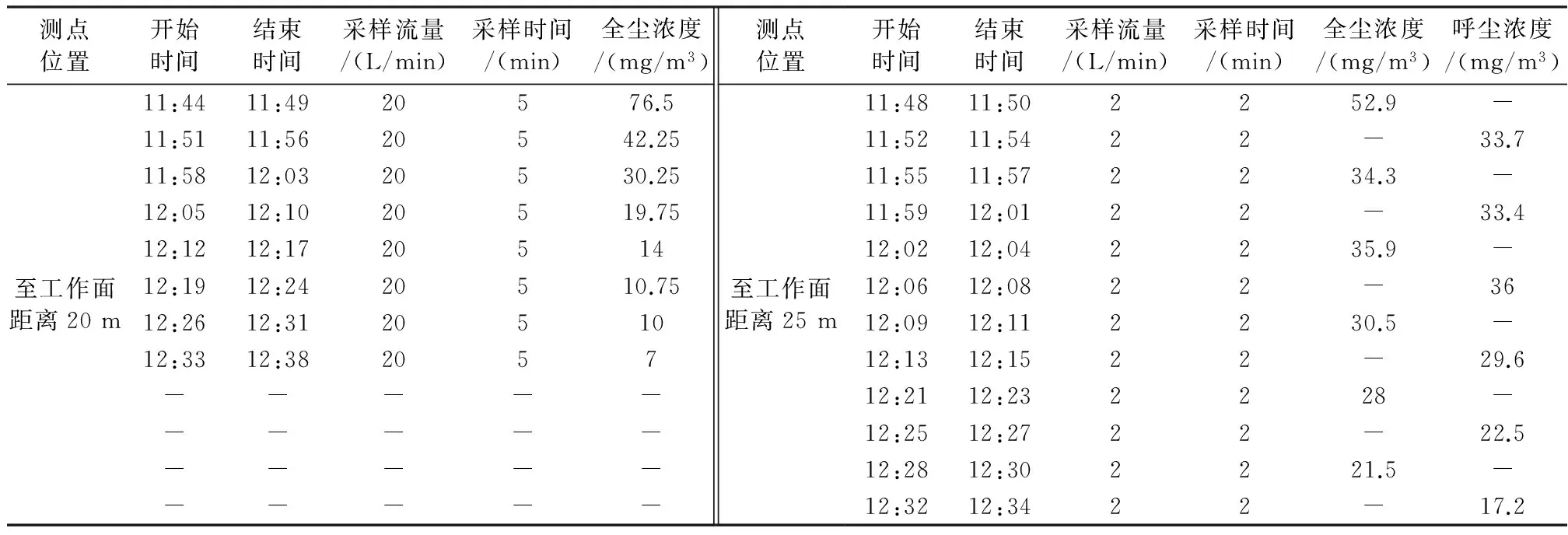
表3 20，25 m处粉尘浓度时间变化实测值

(4)距掘进面10～20 m形成的空气涡旋是粉尘扩散、粒径沉降和浓度时间变化规律发生突变的重要影响因素，这一区间粒径为10～200 μm沉降量偏少，粉尘浓度长时间较高，因此应在此处加强喷雾降尘强度或利用除尘风机进行抽吸，亦或通过改变风筒的布置方式，调整空气流场分布，以避免空气涡流场出现。

[1] 廖贤鑫,蒋仲安,牛 伟.采场爆破粉尘运移规律的Fluent数值模拟[J].安全与环境学报,2012,12(6):43-46.

[2] 蒋仲安,陈梅岭,陈举师.巷道型采场爆破粉尘质量浓度分布及变化规律的数值模拟[J].中南大学学报：自然科学版,2013,44(3):1191-1196.

[3] 陈举师,王 毅,蒋仲安,等.破碎硐室粉尘浓度空间分布规律的数值模拟[J].煤炭学报，2012,38(11):148-152.

[4] 李 锋,撒占友,王 勇,等.基于Fluent的扁平硐室采场粉尘浓度分布及运移规律研究[J].矿业研究与开发,2010,30(5):77-80.

[5] 郑炳旭,魏晓琳.城市爆破拆除的粉尘预测和降尘措施[J].中国工程科学,2002,4(8):69-73.

[6] 许秦坤,陈海焱.爆破粉尘及炮烟控制现状[J].爆破,2010,27(4):113-115.

[7] 王继峰.岩石爆破技术的现状与发展[J].煤矿爆破,2006(75):4-7.

[8] 李怀宇,张兴凯.爆破烟尘初期运动过程的模拟[J].金属矿山,1995(224):19-21.

[9] 孙 佳,蒋仲安,倪 文.爆破烟尘行为的实时模拟[J].爆破,2006,23(1):1-25.

[10] 王福军.计算流体动力学分析—CFD软件原理与应用[M].北京:清华大学出版社,2004.

[11] 俞接成,陈家庆,王 波.液-液分离用水力旋流器内部流场的三维数值模拟[J].石油矿场机械,2007,36(5):9-14.

[12] 蒋仲安,陈举师,王晶晶.胶带输送巷道粉尘运动规律的数值模拟[J].煤炭学报,2012,37(4):659-663.

[13] 黄 磊,吴可家,王振河.煤炭运输转载点粉尘沉降规律的研究[J].选煤技术,2009(3):10-12.

[14] 张 原,桂祥友.基于FLUENT软件的粉尘在水平除尘管道内沉降规律研究[J].矿业工程,2010,8(6):49-52.

Dust Distribution Law of Super-long Roadway in the Process of Digging and Blasting

He Guanghui

(Sihe Coal Mine,Shanxi Jincheng Anthracite Mining Group)

In order to analyze the dust migration laws and guide the design of dust control system in long-distance blasting excavation roadway,based on the 1100 excavation face in a metal mine,a 1∶1 geometric model is established to conduct the CFD simulation,to analyze the air flow field and boundary conditions.According to the model applicability and the air flow field distribution characteristics,the RNG k-ε turbulence model is selected to simulate the air flow field in 1100 excavation working face,the simulation results show the dust volume fraction in the blasting space is low than 10%,which determines that using the discrete phase model to simulate the dust unsteady movement in the blasting space is suitable.The dust diffusion law,dust sedimentation law and dust concentration changing law are obtained in the scope of 0～60 m nearby the excavation face.The results show that the dust concentration decreases when the height increases from 0.5 to 4 m,and the dust concentration distribution has a obvious demarcation in the vertical direction,along the roadway,the dust concentration firstly increases and then decreases.The dust particle with the diameters under 10 μm is evenly distributed in the space,and the sedimentation quantity shows a trend of "decrease-increase-decrease-increase" along the roadway,while for the dust particles with diameters of 10～200 μm,the sedimentation quantity shows a trend of "decrease-increase-decrease".Dust particles with diameters of 15～200 μm almost completely settle.In the early blasting operation within 5 min,the dust concentration along the roadway sharply decreased,and gently decreases with 5～50 min.The high concentration area stays within 0～40 m and dose not migrate along the roadway.The migration laws show that 10～20 m is the air dust jet vortex area which strongly affects dust diffusion,sedimentation and concentration variation.In order to investigate the precision of the simulation results,during the blasting period,the AKFC-92A Dust Sampler and the CCHZ-1000 Automatic dust detector are set up at 20 m and 25 m to detect the dust concentration.The actual measurement values are basically consistent with the simulation values,which indicates the simulation results is reliable.

Long-distance roadway,Blasting,Dust migration,Numerical simulation

2016-06-26)

贺光会(1975—)，男，工程师，048205 山西省晋城市。