基于离散型Hopfield神经网络的联想记忆能力研究 

余洋++傅成华

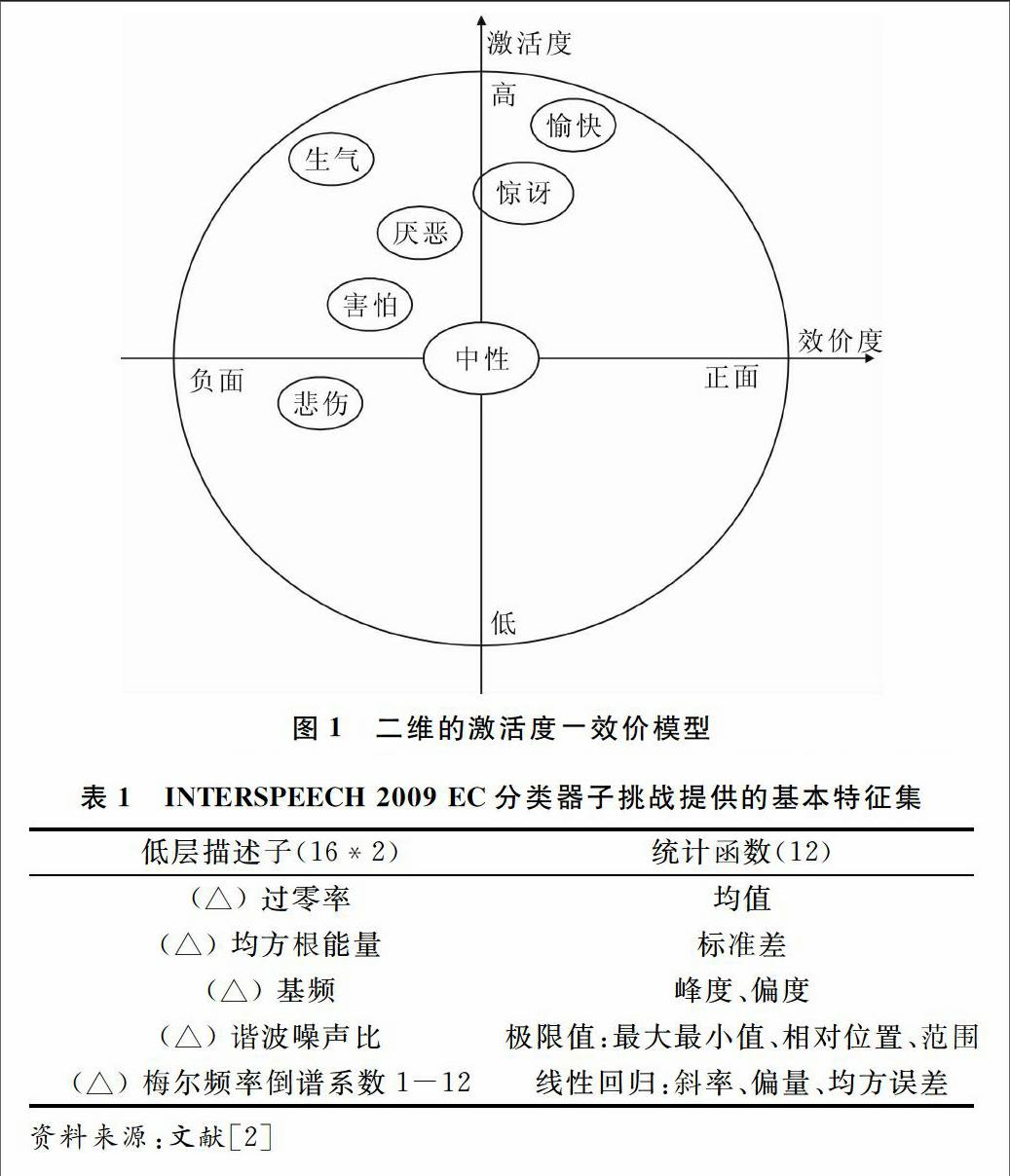
摘要：人工神经网络是对人脑功能的简单抽象和模拟，实质是一种数学模型。它通过大量的简单处理单元互相连接成规模庞大的简单抽象和信息处理系统，能够存储经验知识和联想回忆并使用已存储知识，是目前智能信息处理技术发展的一个主流方向。它可以解决许多传统方法难以解决或无法解决的问题，尤其是那些与记忆、思维、认知、推理及联想相关的问题。主要介绍了离散型Hopfield 神经网络的发展历程、工作原理、使用方法及其联想记忆功能，并通过举例证明了离散型Hopfield神经网络的联想记忆能力。

关键词：人工神经网络；Hopfield神经网络；联想记忆

DOIDOI：10.11907/rjdk.161853

中图分类号：TP391

文献标识码：A文章编号文章编号：16727800（2016）009014603

基金项目基金项目：

作者简介作者简介：余洋（1994-），男，湖北随州人，四川理工学院自动化电子信息学院硕士研究生，研究方向为智能控制；傅成华（1958-），男，四川富顺人，四川理工学院自动化与电子信息学院教授、硕士生导师，研究方向为先进控制与系统优化、神经网络与非线性信息处理。

0引言

Hopfield于1982年提出了一种新型的神经网络——Hopfield网络模型。它采用了与层次型人工神经网络完全不一样的结构特征和学习方法来模拟生物神经网络的记忆机理，首次使用“能量函数”的概念，并且说明了此神经网络与动力学之间的关系，使得判断神经网络在工作过程中的稳定性有了非常简便和可靠的依据。该神经网络非常利于人们理解学习，也可以比较方便地在集成电路中实现。Hopfield神经网络根据网络输入输出的不同分为两种形式：离散型Hopfield神经网络和连续型Hopfield神经网络，两种形式的神经网络应用领域也各不相同。本文使用离散型Hopfield神经网络实现联想存储器设计。

1离散型Hopfield神经网络

离散型Hopfield神经网络是由n个神经元相互连接而成的二值神经网络[12]，并且各神经元之间的连接是双向的，连接强度用权值表示。网络的全互联结构如图1所示。神经元的输出为离散值0（或-1）和1，分别代表神经元的抑制和激活状态。由于神经网络的时间离散特性，因而其被称为离散型Hopfield神经网络[3]。

这种连接方式使得离散型Hopfield神经网络中每个神经元的输出均通过神经元之间的连接权值反馈到同一层次的其它神经元，并作为该神经元的输入，从而使各神经元之间相互制约，保证离散型Hopfield神经网络在没有外部输入的情况下也能进入稳定状态。

两个互联神经元之间的连接权值相同（wij=wji），每个神经元到其自身的连接权值为0，即wii =0。

1.1处理单元模型

离散型Hopfield神经网络的单个神经元结构如图2所示，单个神经元采用M-P模型进行信息处理，假设神经网络有n个神经元，以xj表示神经元j的输出（也称为神经元的状态），wij表示神经元i与神经元j之间的连接权值，θj表示神经元j的阈值。

神经元j的净输入sj=∑ni=1xiwij-θj（1）

神经元j的输出 xj=f（sj）=sgn（sj）=1sj>0-1sj≤0（2）

1.2网络状态及运行规则

离散型Hopfield神经网络的状态由网络所有（n个）神经元的状态集合构成，在任意一个给定的时刻t，离散型Hopfield神经网络的状态表示为：

X（t）=（x1 ，x2 ，…，xn ）（3）

离散型Hopfield神经网络是全互联反馈式的连接结构，每个神经元都会接收到全部神经元的反馈信息，故当网络中的各神经元状态改变时，整个网络状态也随之变化。当网络中各神经元的输出状态都不再改变时就表示网络达到稳定状态（即xj （t+1）=xj （t）=f（sj （t）））。神经网络要达到稳定状态需要经过反复更新，学习训练。

离散型Hopfield神经网络的工作过程就是网络状态的动态演化过程，即从网络初始状态沿能量递减的方向不断演化的过程，直到达到网络的稳定状态，这时网络的稳定状态就是网络的输出。离散型Hopfield神经网络工作时有以下运行步骤：①对网络进行初始化；②从网络中随机选取一个神经元i；③按照式（1）计算神经元i在t时刻的净输入si （t）；④按照式（2）计算神经元i在t+1时刻的输入xi（t+1），此时网络中除i以外的其它神经元j的输出保持不变，即xj（t+1）=xj（t）其中i ≠j；⑤按照式xj（t+1）=xj（t）=f（sj（t））判断网络是否达到了稳定状态，如果未达到稳定状态就转到②继续进行，如果网络达到稳定状态则网络的工作过程终止。

1.3离散型Hopfield神经网络的能量函数

Hopfield神经网络的一大特点就是引入了“能量函数”，它表明了神经网络与动力学之间的关系。上文也提到，网络运行时在网络状态不断变化过程中，网络的能量值不断递减，直到达到稳定状态。这说明网络的能量值与网络的稳定状态有着十分密切的关系。能量函数定义为：

E=-12∑ni=1∑nj=1wijxixj+∑ni=1θixi（4）

Hopfield神经网络实际上是一个非线性动力系统，网络按动力学方式运行，网络状态的变化过程实际上是使能量极小化的过程：每次神经元状态改变时，整个网络的能量应单调递减，即能量与以前相同或下降。证明如下：

设任一神经元j由式（4）得神经元j的能量为：

Ej=-12∑ni=1wijxixj+θjxj（5）

该式可变换为：

Ej=-12xj∑ni=1wijxi+θjxj（6）

由t时刻到t+1时刻神经元j的能量变化为：ΔEj=Ej（t+1）-Ej（t）= -Δxj（∑ni=1wijxi-θj）+12Δxj∑ni=1wijxi（7）

由于在t+1时刻只有神经元j调整状态，并且各神经元不存在自反馈，式（7）可简化为：

ΔEj= -Δxj（∑ni=1wijxi-θj）（8）

在t+1时刻共有以下3种可能情况来分析ΔEj的大小从而论证网络能量值的改变方向：①如果神经元j的状态不发生变化，即xj （t+1）=xj （t），则Δxj=0，由式（8）可知ΔEj=0；②如果神经元j的状态发生变化，是从-1变为1，则Δxj=2，此时由式（1）和式（2）可知∑ni=1wijxi-θj>0，再由式（8）得ΔEj<0；③如果神经元j的状态发生变化，是从1变为-1，则Δxj=-2，此时由式（1）和式（2）可知∑ni=1wijxi-θj≤0，再由式（8）得ΔEj≤0。

综上可知，从t时刻到t+1时刻，无论神经元j的状态如何变化，其能量的改变量均为ΔEj≤0。由于神经元j是网络中任意一个神经元，而网络中的神经元又都是按照同一规则来更新状态的，因而整个网络的能量一直向减少的方向进行。网络变化的过程就是网络能量的极小化过程，因为能量函数是有界的，故网络一定会趋于稳定状态，该稳定状态就是网络的输出。离散型Hopfield神经网络能量函数的变化曲线如图3所示，能量函数的变化过程可以看作是下坡的过程，当网络的状态随时间改变时，整个网络的能量沿着下降最快的方向改变，最终停在整个网络能量的极小点[4]。这些极小点有全局极小点c，也有局部极小点a、b，最终落入哪种极小点取决于网络的初始状态。网络能量函数变化曲线如图3所示。

1.4关于离散型Hopfield神经网络联想记忆的连接权值设计

离散型Hopfield神经网络可以应用于联想记忆[5]，其联想记忆的基本原理是利用能量函数的极值点，网络将记忆的样本信息存储在不同的能量极值点上，当网络输入某一种模式时，网络工作到稳定状态后能够“联想记忆”出与其相关的其它存储样本，从而实现联想记忆。并且神经网络都有很好的容错性能，即使是对一些不全的、破损的、变形的输入信息，网络也能够很好地将其恢复成比较完整的原型信息。记忆是联想的前提，必须先将信息存储起来，才能按照某种方式或规则再取出相关信息，能量极值点存储记忆模式，而网络的连接权值和阈值决定这些极值点的分布，因此网络联想记忆的关键就是根据能量极值点和需要被记忆的模式设计一组恰当的网络连接权值和阈值。

网络在没有记忆之前是空白状态，只有设计了恰当的连接权值和阈值才会使网络具有知识，连接权值的设计调整过程就是网络的学习过程。离散型Hopfield神经网络一般用Hebb规则的外积和法来设计权值。方法具体如下：

假设网络共有n个节点，W是网络的连接权矩阵，如果网络一共处理m个两两正交的模式样本，则网络的学习记忆集合为xk=（xk1，xk2，…，xkn）（k=1，2，…，m）。

（1）若m=1只有一个学习模式，学习记忆集合为X1，对于输入模式X1，如果网络达到稳定状态，有：

X1=sgn（XW），即x1j=sgn（∑ni=1wijx1i）j=1，2， …，n（9）

由sgn函数的特点可知，若满足x1j（∑ni=1wijx1i）>0，即若连接权值wij正比于x1jx1i，则式（9）成立。综合可得，网络的连接权值与输入模式向量的每个分量之间满足关系：

wij=αx1jx1iα为常数而且大于零（10）

（2）如果有多个学习模式，则可将式（10）进行推广有：

wij=α∑mk=1xkjxkiα为常数而且大于零（11）

由wii=0可将式（11）改写为：

W=α∑mk=1[（Xk）TXk-I]α为常数而且大于零，I为nxn的单位矩阵（12）

在设计好网络连接权矩阵后，网络就处于正常工作状态，加载输入模式向量时，网络可以进行模式的记忆及联想。

2联想记忆功能实现证明

联想记忆的过程分为两个阶段：第一阶段是记忆阶段（也称存储阶段、学习阶段），它是联想记忆的关键，其处理过程是将记忆模式作为网络的稳定状态，并通过设计或学习获得需要的网络连接权值；第二阶段是联想阶段（也称回忆阶段），此阶段是利用网络进行回忆，将给定的输入模式作为网络的初始状态，网络按照既定的运行规则不断演化，一直演化到网络的稳定状态，此时网络的稳定状态就是回忆出的记忆模式。下面举例证明离散型Hopfield神经网络是如何实现联想记忆功能。设有一个4神经元的离散型Hopfield神经网络，各神经元的阈值为0，其中存储了两个模式，模式一X1为（1，1，1，1），模式二X2为（-1，-1，-1，-1），每个存储模式由两部分组成：名称和颜色。前两神经元存储的是名称，后两个神经元存储的是对应的颜色。模式一表示“蓝色的天空”，前两个1表示天空，后两个1表示蓝色的；模式二表示“绿色的树”，前两个-1表示树，后两个-1表示绿色的，当网络上加载信息不全或错误地输入模式三X3=（1，1，-1，1）时，让网络联想记忆输出模式X1。若想让网络联想输出模式X1，必须首先设计网络的连接权值，让网络记忆模式一和模式二，然后让网络加载输入模式三运行到稳定状态。将网络要存储的模式一和模式二设计为网络的两个稳定状态，由此设计网络的连接权值。根据式（12），设α=1得网络的连接权矩阵为；

W=（X1）TX1+（X2）TX2-2I=0222202222022220

设计好连接权值后，将模式三加载至网络，然后按照网络运行规则让网络运行：

t=0：网络的初始状态X（0）=（1，1，-1，1）；

t=1：选取节点1，节点1的状态为x1（1）=sgn[1×0+1×2+（-1）×2+1×2]=sgn[2]=1

网络状态X（1）=（1，1，-1，1）；

t=2：选取节点2，节点2的状态为x2（2）=sgn[1×2+1×0+（-1）×2+1×2]=sgn[2]=1

网络状态X（2）=（1，1，-1，1）；

t=3：选取节点3，节点3的状态为x3（3）=sgn[1×2+1×2+（-1）×0+1×2]=sgn[6]=1

网络状态X（3）=（1，1，1，1）；

t=4：选取节点4，节点4的状态x4（4）=sgn[1×2+1×2+1×2+1×0]=sgn[6]=1

网络状态X（4）=（1，1，1，1）；………

按此规则循环运行下去直到网络状态不再改变，网络处于稳定状态，网络的输出就是（1，1，1，1），也即网络存储的记忆模式一X1=（1，1，1，1）。同理，当网络加载模式四X4=（-1，-1，1，-1）时，网络也可联想记忆输出模式二。从而证明了离散型Hopfield神经网络具有联想记忆功能。

3结语

神经网络的联想记忆功能虽然很强，但是也存在一些缺陷。由于联想记忆能力受到了记忆容量和样本差异的制约，当记忆的模式较多且容易混淆时，网络不能够很好地辨别出正确模式，而且达到的稳定状态也往往不是记忆住的模式。并且，所有记忆模式不是以同样的记忆强度回想出来的。

参考文献参考文献：

[1]周非.基于RBF网络和逆模型的汽油机瞬态空燃比控制[D].成都：西华大学，2006.

[2]于乐斐.两类时滞细胞神经网络的稳定性分析[D].青岛：中国海洋大学，2008.

[3]夏松.Hopfield神经网络构造的联想记忆存储器实现与研究[D].合肥：安徽大学，2010.

[4]周超超.人工智能专家系统在曲轴圆角滚压校直中的研究[D].武汉：武汉理工大学，2003.

[5]颜本伟.基于小世界体系的模糊自联想记忆神经网络研究[D].重庆：西南大学，2011.

责任编辑（责任编辑：孙娟）