认知多址接入系统中的能量消耗优化研究

谢显中，肖正瑛，张森林

(重庆邮电大学 个人通信研究所，重庆 400065)



认知多址接入系统中的能量消耗优化研究

谢显中，肖正瑛，张森林

(重庆邮电大学 个人通信研究所，重庆 400065)

考虑认知多址接入系统中的多个次用户与主用户同时共享多个信道的能量消耗问题，次用户能够同时感知和接入多个主用户信道并把对主用户的干扰维持在一定的范围内。为了减少能量消耗，需要对感知时间、信道以及功率进行合理的分配，同时，把干扰功率作为约束条件以保证主用户的服务质量。在基于多用户多信道感知的频谱共享方案中，所建立的初始优化问题为非凸整型组合分式规划问题，为了对感知时间、信道及功率进行联合优化，将其进行凸松弛并进一步转化为一个含参数的线性问题，从而提出一种最小化能量消耗的算法。通过实验仿真讨论次用户数量，信道数量及干扰功率对能量消耗和最优感知时间的影响，同时也验证了分析结果。

认知无线电；多址接入；频谱共享；能量消耗

0　引　言

近年来，频谱的稀缺以及大部分授权频谱的低利用率促进了认知无线电(cognitive radio，CR)[1]技术的发展，在保证主用户(授权用户)不受到有害干扰的条件下，认知无线电通过使次用户(非授权用户)接入授权频谱来提高频谱利用率。次用户接入授权频谱有3种方式。第1种为机会频谱接入(opportunistic spectrum access，OSA)[2]：次用户只有在检测到主用户信道空闲时才接入；第2种为频谱共享(spectrum sharing，SS)[3]：采用干扰功率作为约束条件来保证主用户的QoS，使次用户能够与主用户同时接入相同的授权频谱；第3种为基于感知的频谱共享(sensing-based SS)[4]：次用户首先进行频谱感知，然后根据感知结果决定发送信号功率的大小。本文针对基于感知的频谱共享方式，它是机会频谱接入与频谱共享的结合[5]，通过感知时间和传输时间的折中，在吞吐量方面能够获得更好的性能。

由于人们对高速率无线服务需求的持续增长，当前的无线系统在能量消耗方面面临着巨大的挑战。特别是对于依靠电池供能的移动终端，由于电池技术的发展滞后于无线技术的发展，能量消耗问题显得更加严重。因此，本文将关注认知无线电传输中的能量消耗问题和能量有效性(energy efficiency, EE)。对于基于感知的认知无线电系统，为了保证主用户的服务质量，当一个数据帧长度固定时，为了减少能量消耗，除开合理设计感知时间和数据传输时间外，优化分配信道和功率也十分重要，文献[6-20]进行了该方面的探讨。

文献[6]在机会频谱接入下，采用有序的信道感知来研究最大化能量效率问题。其中，次用户每次只能在一个信道上进行感知和发送数据。文献[7]在多输入多输出(multiple-input multiple-output，MIMO)认知多址接入信道下，采用连续干扰消除(successive interference cancellation, SIC)技术并通过设计预编码矩阵来研究加权的能量效率最大化问题。由于SIC技术可以处理次用户之间的干扰问题，因此，简化了理论分析。但是，当具有SIC技术的解码器不可用或者为了减少硬件(解码器)复杂度时，那么就需要通过合理的分配信道来避免次用户之间的干扰。在总传输预算和对主用户干扰门限约束下，文献[8-13]分别利用整数规划/分数规划、拟凸性和变分理论来优化资源分配和能量效率，对正交频分复用(orthogonal frequency division multiplexing, OFDM)的时频资源进行了详细分析，并讨论了频谱感知存在错误及信道不确定的情况。为了最大化能量有效性，将主用户资源占用建模为马尔科夫过程，文献[14]给出了基于部分可观测马尔可夫过程(partially observable markov decision processes, POMDP)的联合感知和传输策略，文献[15]在考虑QoS的条件下得到了联合感知和功率分配方案。为解决次用户感知增加的能量消耗问题，文献[16]通过优化感知时间来改进能量有效性，并利用黄金分割得到最优解。针对多个次用户选择感知多个信道(即多对多)的情况，文献[17]联合考虑信道容量、期望检测概率及信噪比，利用复杂的3步方法解决多信道调度问题以实现能耗、性能与频谱机会均衡；文献[18]在信道保护约束下最小化感知过程总能耗，通过调度用户信道组决定对应的感知时长，以及能量与感知准确度的均衡；文献[19]研究了最大化能量有效性的感知分配调度方案，并基于M-凸概念给出了低复杂度的次优解。此外，文献[20]同时考虑了能量有效性和频谱有效性问题。

通过上述分析，除文献[17-19]外，目前的研究很少考虑基于多用户多信道感知的频谱共享(即次用户能够同时感知和接入多个信道的场景)的能量消耗问题和传输方案。但是，文献[17-19]主要关注多信道的协作感知调度问题，仅对频谱感知和感知结果报告的能量消耗优化，没有结合传输数据的能量消耗。此外，文献[17-18]在报告时假设所有次用户的信噪比是服从某一分布随机产生的，这不完全适合实际网络拓扑，同时，文献[19]的优化目标不是能量消耗/能量效率。

针对上述分析，本文将考虑一种基于多用户多信道感知的频谱共享(multi-users multi-channels sensing-based SS，MMSSS)方案。定义平均能量消耗与平均发送数据的比值为能量消耗的性能指标，在约束条件下建立初始的优化问题。为了对感知时间、信道及功率分配进行联合优化，将其进行凸松弛并进一步转化为一个含参数的线性问题，通过所提出的优化算法来获取最优解。实验仿真分析相关因素对能量消耗和最优感知时间的影响并与多用户多信道的机会频谱接入(multi-users multi-channels OSA，MMOSA)方案进行对比，从而验证该文的分析。

1　系统模型

假设认知无线电系统由K个次用户和N个主用户信道组成，并且K个次用户能够同时接入这N个主用户信道，即构成一个认知多址接入系统。由于次用户在接入主用户信道之前会进行频谱感知，因此，次用户的一个数据帧周期就包含感知时间和数据传输时间。数据帧周期和感知时间分别用T和τ表示，那么一个帧周期内次用户的数据传输时间就为T-τ。由于能量检测的优点，本文假设次用户利用能量检测方案，且能够同时进行多个信道的频谱感知。

(1)

(1)式中：τ为感知时间；γn为次用户接收机在信道n上接收到的信噪比(signal noise ratio，SNR)；fs表示抽样频率；φd,n表示次用户在信道n的检测概率。

2　信道和功率分配

(2)

认知无线电系统中的能量消耗包括发送信号功率，电路功率(即信号处理和其他部分产生的能量消耗)。例如，模数/数模(AD/DA)转换，变频器，混频器，合成器等[21]。因此，一个数据帧周期内的功率消耗为[22]

(3)

(4)

(3)-(4)式中：ζ为功率放大器(power amplifier，PA)的转换效率；ξ为功率放大器的峰均比(peak to average ratio，PAR)；Pc为电路功率。由于频谱感知是非理想的，因此，基于频谱感知的结果和主用户在每个信道的实际状态，次用户分别有4种不同的瞬时传输速率。用传输速率r的第1个下标表示主用户的实际状态(0表示空闲，1表示占用)，第2个下标表示次用户的判决结果(0表示空闲，1表示占用)。

当次用户成功检测到主用户的空闲状态时，第k个次用户在信道n的速率为

(5)

当次用户没能检测到主用户的空闲状态时，第k个次用户在信道n的速率为

(6)

当次用户没能检测到主用户的占用状态时，第k个次用户在信道n的速率为

(7)

当次用户成功检测到主用户的占用状态时，第k个次用户在信道n的速率为

(8)

(5)-(8)式中：Pp,n为主用户在信道n的发送信号功率；σ2=N0BNf为接收机端的噪声，其中，N0为单边功率谱密度，B为信道带宽，Nf为噪声系数。因此，次用户k在信道n上的平均吞吐量为

(9)

(9)式中，

(10)

(10)式中：H0,n为主用户在信道n的空闲概率;H1,n为主用户占用信道n的概率。由(9)式可以得到次用户k在N个信道上，一个帧周期内平均发送的数据为

(11)

那么K个次用户在N个信道上，一个帧周期的平均发送的数据就为

(12)

(12)式中：E[·]表示期望运算；P(0)和P(1)为功率分配矩阵。次用户k在信道n的平均功率消耗为

(13)

因此，次用户k在N个信道上，一个帧周期的平均能量消耗为

(14)

(14)式中：Psens为感知功率。K个次用户在N个信道上，一个帧周期的平均能量消耗为

(15)

由于次用户受到自身的功率预算限制，考虑平均发送功率约束是十分必要的。其约束条件可以表示为

(16)

(16)式中，

(17)

(17)式中，Pm表示次用户的最大平均发送功率。

认知无线电系统中，保证主用户的服务质量具有最高优先级，需要考虑次用户对主用户的干扰。根据前面的分析，次用户k的平均干扰功率约束可以表示为

(18)

(18)式中，PL为主用户在信道n上能够容忍的最大平均干扰功率。综上所述，能量消耗优化问题可以表述为

(19)

3　优化算法

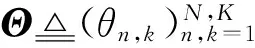
(20)

因此，(5)-(8)式的速率表达式修改为

(21)

(22)

(23)

(24)

(25)

由于感知时间τ在(0,T)，可以采用一维的穷举搜索来获得最优感知时间，其表示为

(26)

然后，最优的信道及功率分配U*，P(0)*，P(1)*表示为

(27)

对于U，P(0)和P(1)，(25)式是一个非线性分式规划问题。利用分式规划理论，引入一个参数λ，将其转化为一个含参数的线性问题，得到函数

(28)

这里，τ被当成一个常量。定义

(29)

根据Dinkelbach的关于非线性分式规划的研究[24]，当且仅当

(30)

则(25)式和(28)式的关系为

(31)

证明如下。

1)充分性。

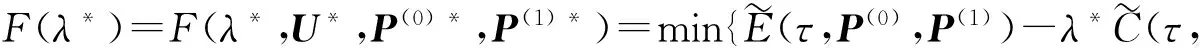
2)必要性。

证明完毕。

由此可得，λ*为(25)式的解，即最小值，且在(U*,P(0)*,P(1)*)处取得。下面，将介绍如何求解λ*。需证明F(λ)是一个关于λ的单调递减函数。

设λ1<λ2，

(32)

因此，F(λ)是一个关于λ的单调递减函数。在一个包含λ*的区间[λmin,λmax]，采用二分法来找出λ*。算法步骤如下。

步骤1确定区间[λmin,λmax]，验证F(λmin)·F(λmax)<0，给定精确度ε；

步骤2λ=(λmin+λmax)/2；

步骤3采用凸优化技术[25]，求解(28)式，并计算出F(λ)；

步骤4若F(λ)=0，则λ=λ*；若F(λmin)·F(λ)<0，则令λmax=λ；若F(λ)·F(λmax)<0，则令λmin=λ；

步骤5判断是否达到精确度。若|λmin-λmax|<ε，则得到λ*，否则，重复步骤2-步骤4。

参数ε是预先设定的一个极小值，只要确定了λ*，那么也将获得对应的最优信道及功率配置。

4　仿真结果与分析

本文的MMSSS方案中，数据帧周期T=100 ms，抽样频率为6 MHz，每个信道的带宽为6 MHz且不相互重叠。对于所有的信道，次用户感知时所接收到的信噪比(最差情况)为-20 dB，次用户的检测概率为0.9。次用户的最大平均发送功率Pm为10 dBW，主用户在信道n上的发送功率Pp,n为10 mW。双边噪声功率谱密度N0/2为-204 dBW/Hz，噪声系数Nf为10 dB，感知功率Psens为110 mW，电路功率Pc为210 mW，功率放大器的峰均比ξ为6 dB，转换效率ζ为0.35。

图1为不同信道数目下感知时间对能量消耗的影响。主用户信道的空闲概率H0,n=0.8，最大平均干扰功率PL=-5 dBW，次用户数目K=5。从图1中可以看出，能量消耗是关于感知时间τ的一个凸函数，存在最优的τ。此外，最小能量消耗的值随着信道数目的增加而减少。这是因为，当信道数目增加时，较高质量的信道(次用户链路之间增益较高，而次用户到主用户以及主用户到次用户链路之间增益较低)数目也会随之增加，通过合理的信道与功率分配就能够获得更大的收益，从而提高能量效率。虽然能量消耗随着信道数目的增加而减少，但是最优感知时间只在很小的范围内变化，这一特点对于设计网络协议十分有用。例如，对于不同的信道数目，可以设定一个固定的最优感知时间，以减少硬件参数的调整。

图2为不同次用户数目下感知时间对能量消耗的影响。主用户空闲概率和最大平均干扰功率与图1设置相同，信道数目N=9。从图2中可以看出，最小能量消耗随着次用户数目增加而增加。虽然信道数目不变，但是次用户数目的增加，导致次用户之间竞争加剧，相对于每个次用户来说，消耗了相同的感知能量，可分配的信道数目却减少了。因此，信道与功率分配的收益就会降低，从而使能量消耗增加。从图2中还可以看出，最优感知时间与图1具有相同的特点。

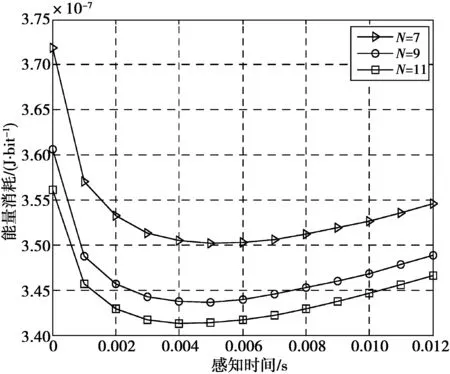
图1　不同信道数目下感知时间对能量消耗的影响Fig.1　Energy consumption versus sensing time under different number of channels

图2　不同次用户数目下感知时间对能量消耗的影响Fig.2　Energy consumption versus sensing time under different number of secondary users

图3为不同平均干扰功率约束下感知时间对能量消耗的影响。H0,n=0.8，N=9，K=5。当主用户能够容忍更高的干扰功率时，能量消耗和最优感知时间同时减少。当干扰约束条件越苛刻时，为了减少对主用户的干扰，次用户需要花费更长的时间感知信道来获得更高的频谱感知准确度。

图4为MMSSS方案与MMOSA方案(即MMSSS中，Pn,k(1)=0)进行比较，后者在实际的认知无线电系统中被广泛地应用，其严格禁止次用户与主用户在相同的信道同时进行传输。这里，N=9，K=5。从图4中可以看出，在相同的主用户空闲概率下，MMOSA比MMSSS消耗了更多的能量。由于在相同的发送功率预算下，MMSSS使次用户有更多的机会发送数据，提供了更高的吞吐量。因此，能量消耗比MMOSA低。如果干扰功率约束越苛刻，2种方案之间的差距越小。这是因为当干扰功率约束门限值非常低时，次用户检测到主用户活跃时只能采用更低的Pn,k(1)，几乎接近于0，使其只能发送很少的数据，导致MMSSS中的次用户的发送功率主要被分配在检测到主用户空闲的时间段，几乎与MMOSA相同。当主用户的空闲概率越小时，2种方案之间的差距会越大。这表明在实际的网络中，当主用户很少空闲时，MMSSS将具有更大的优势，这一点是十分重要的。因此，在未来空闲频谱越来越少时，MMSSS是一种提高频谱效率的重要方案。

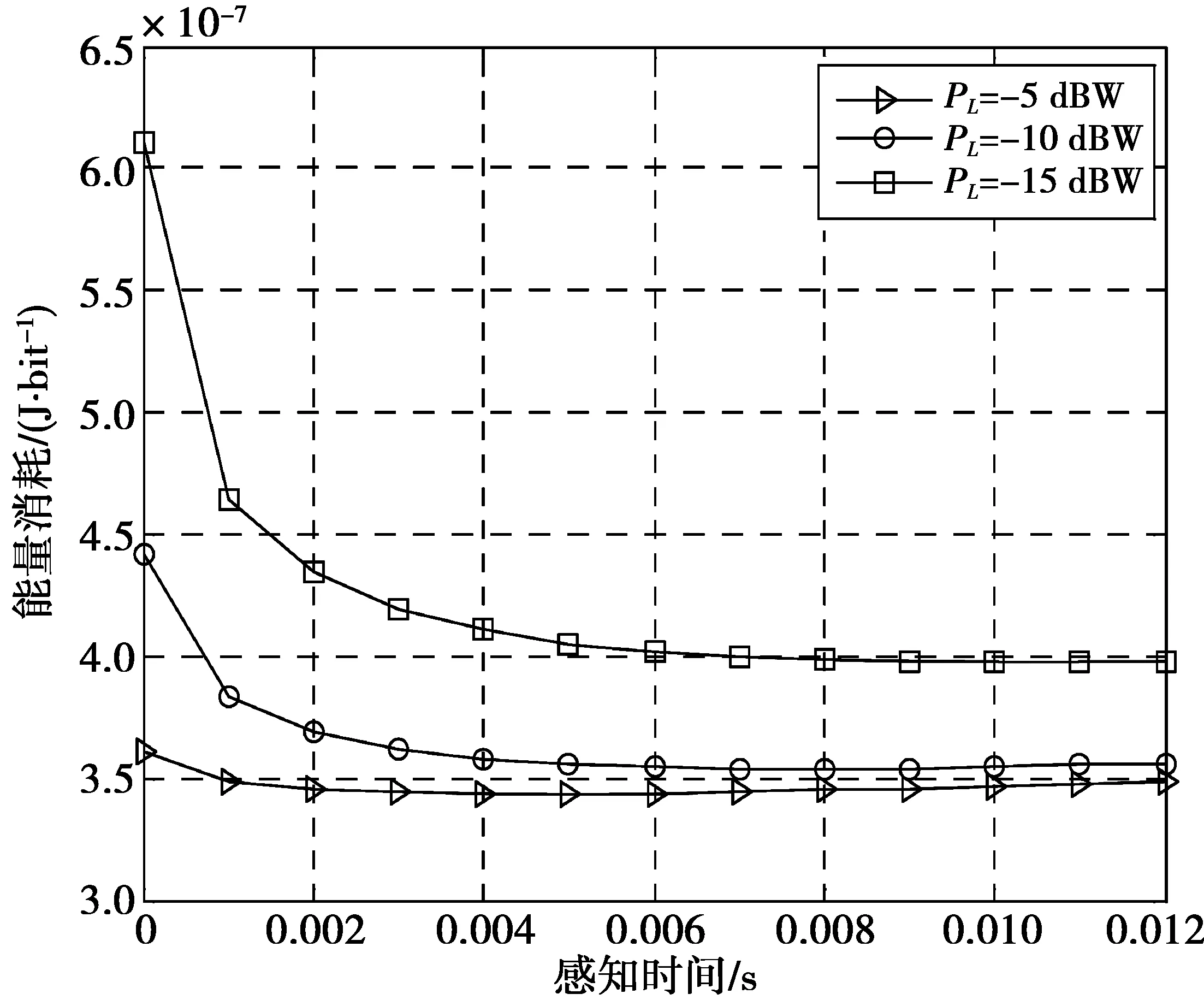
图3　不同平均干扰功率约束下感知时间 对能量消耗的影响Fig.3　Energy consumption versus sensing time under different average interference power constraint

为了更好地比较MMSSS与MMOSA的性能，把2种方案下的感知时间与能量消耗的关系放在了同一张图上。图5中，K=5，H0,n=0.8，PL=-5 dBW。图6中，N=9，K=5，H0,n=0.8。从图5，图6中可以看出，MMSSS方案的性能优于MMOSA方案。当干扰功率门限值越小时，2种方案之间的差距越小。这是因为，对于MMSSS方案，当主用户占用信道时，为了保护主用户系统，次用户发送数据的机会就会随着干扰功率门限值降低而减少。因此，总结出MMOSA为MMSSS的一个特例，即MMSSS中次用户检测到主用户占用信道时，发送功率为0。

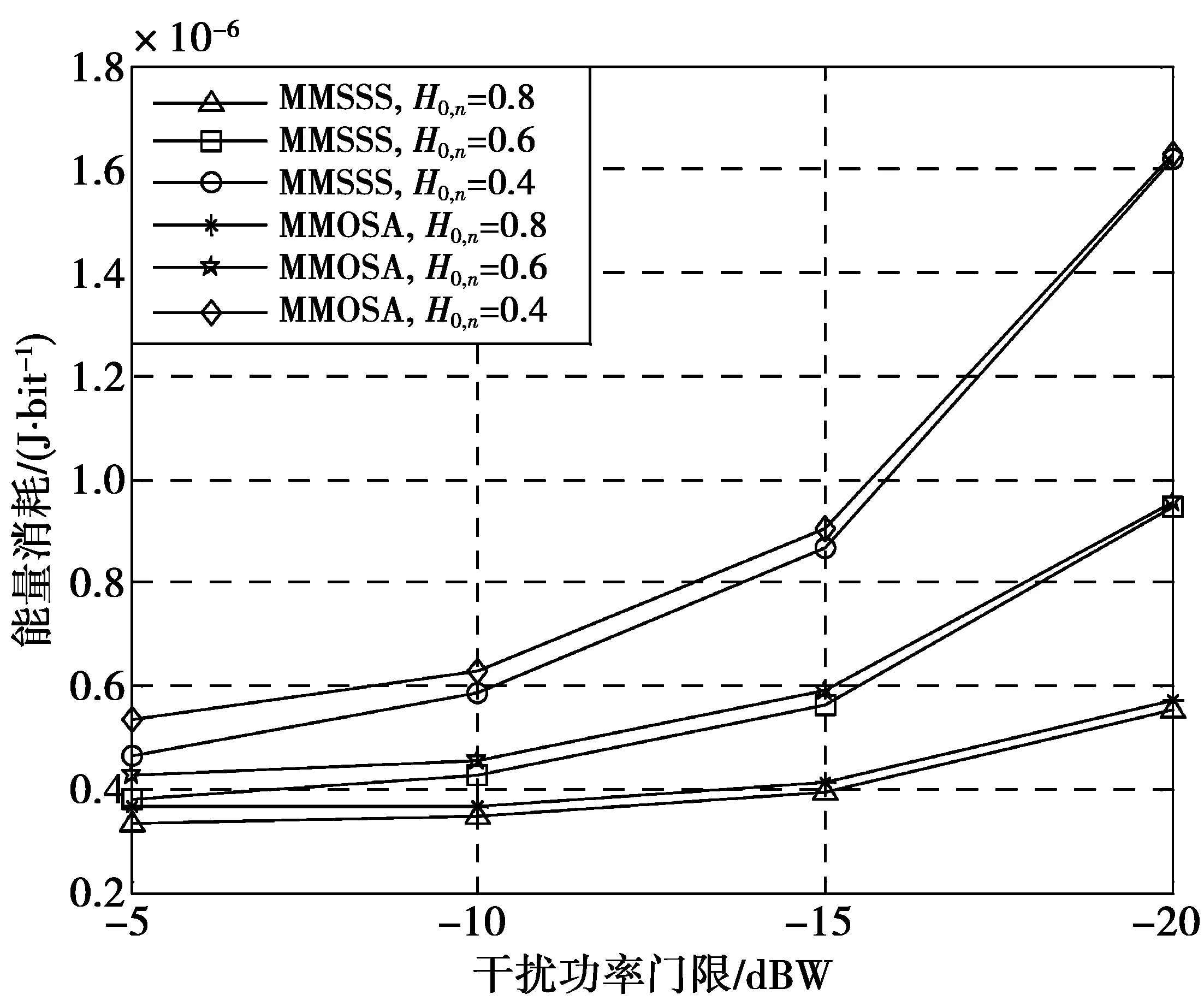
图4　不同主用户空闲概率下干扰功率门限对 能量消耗的影响Fig.4　Energy consumption versus interference power under different primary user idle probability

图5　不同信道数目下感知时间对能量消耗的影响Fig.5　Energy consumption versus sensing time under different number of channels

图6　不同平均干扰功率约束下感知时间对能量消耗的影响Fig.6　Energy consumption versus sensing time under different average interference power constraint

图7和图8分别为在H0,n=0.6，H0,n=0.4下感知时间对能量消耗的影响。其中，N=9，K=5。从图7，图8中也可以看出，MMSSS方案的能量消耗低于MMOSA方案。从图6—图8可以得出，最优感知时间随着H0,n值的减少而增加，这是为了确保有害干扰功率在约束条件范围内。当H0,n=0.4时，2种方案在最优感知时间时的性能差距大于H0,n=0.8和H0,n=0.6时的差距，这同样证实了前面图4中的分析。

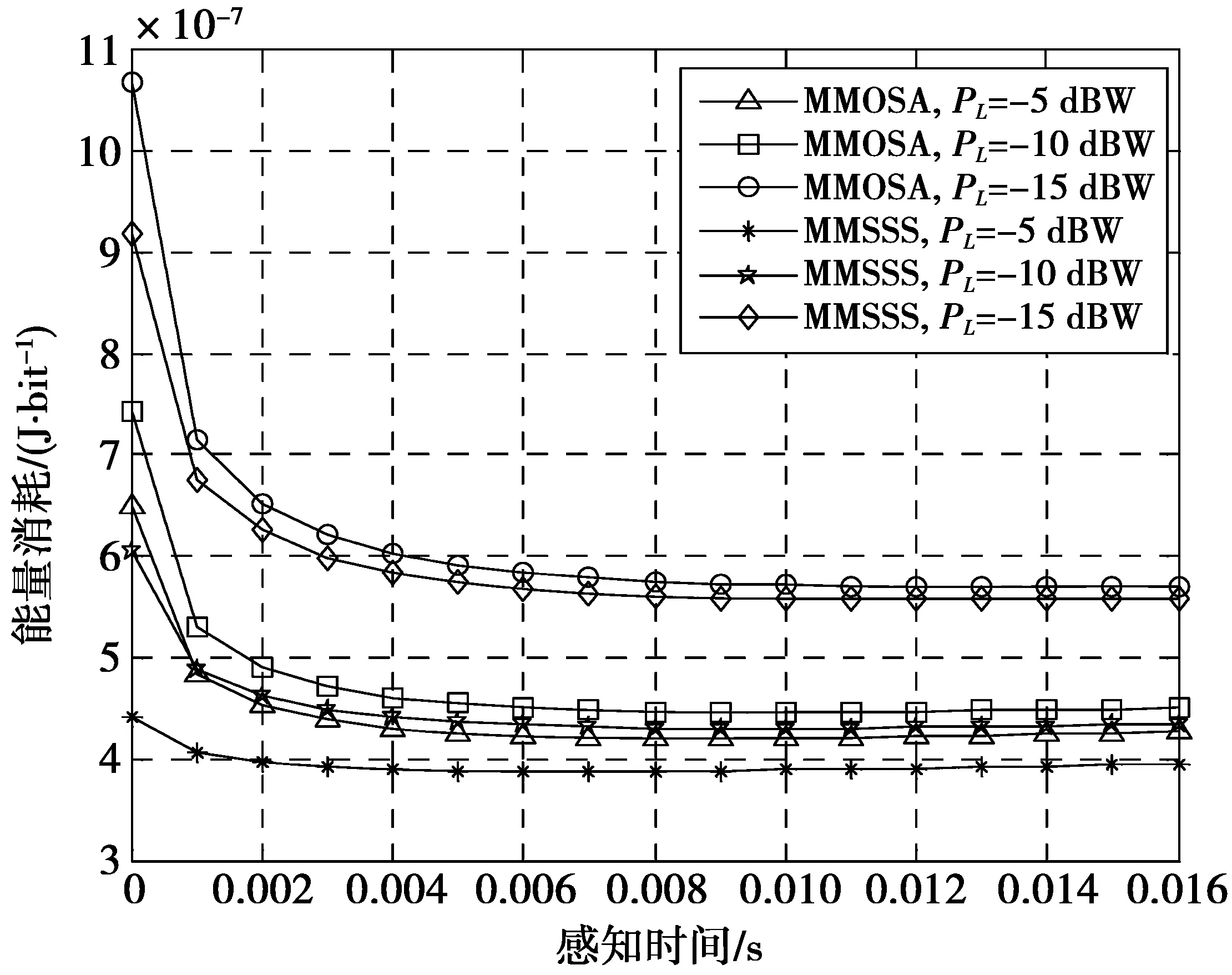
图7　不同平均干扰功率约束下感知时间 对能量消耗的影响Fig.7　Energy consumption versus sensing time under different average interference power constraint

图8　不同平均干扰功率约束下感知时间 对能量消耗的影响Fig.8　Energy consumption versus sensing time under different average interference power constraint

5　结束语

对于一个高效节能的认知无线电系统，如何设计最优的感知时间、信道和功率分配方案是一个十分重要的课题。本文研究了相关问题，并且在次用户的平均发送功率约束和主用户的干扰功率约束下，提出了一种MMSSS方案下能够获得最优感知时间、信道和功率分配的算法。通过改变次用户数目，信道数目，干扰功率门限值以及主用户占用信道概率来评估MMSSS方案的系统性能。实验结果表明，对于不同的次用户数目和信道数目，最优感知时间并不会发生很大变化。为了更好地保护主用户，当平均干扰功率约束较苛刻，或者授权信道的空闲概率较低时，最优感知时间将会随之延长。除此之外，MMSSS方案比MMOSA方案具有更好的性能，随着空闲频谱不断减少，前者的重要性将更大。

[1]MITOLA J, MAGUIRE G Q. Cognitive radio: making software radios more personal[J].IEEE Personal Communications, 1999, 6(4):13-18.

[2]GHASEMI A, SOUSA E S. Spectrum sensing in cognitive radio networks: the cooperation-processing tradeoff[J]. Wireless Communications and Mobile Computing, 2007，7(9):1049-1060.

[3]ASGHARI V, AISS S. Spectrum sharing in cognitive radio systems: service-oriented capacity and power allocation[J]. IET Communications, 2012, 6(8):889-899.

[4]KANG X, LIANG Y C, GARG H K, et al. Sensing-based spectrum sharing in cognitive radio networks[J]. IEEE Transactions on Vehicular Technology, 2009, 58(8):4649-4654.

[5]LIANG Y C, ZENG Y, PEH E C Y, et al. Sensing-throughput tradeoff for cognitive radio networks[J]. IEEE Transactions on Wireless Communications,2008，7(4): 1326-1337.

[6]PEI Y, LIANG Y C, THE K C, et al. Energy-efficient design of sequential channel sensing in cognitive radio networks: optimal sensing strategy, power allocation and sensing order[J]. IEEE Journal on Selected Areas Communications,2011,29(8):1648- 1659.

[7]HUANG Guangjie, JITENDRA K T. On precoding for maximum weighted energy efficiency of MIMO cognitive multiple access channels[C]//IEEE.IEEE GLOBECOM. Atlanta:IEEE Press, 2013:1044-1049.

[8]WANG Shaowei, MENGYAO G, ZHAO Wentao.Energy-efficient resource allocation for OFDM-based cognitive radio networks[J].IEEE Transactions on Communications,2013,61(8):3181-3191.

[9]LU L, HE Dawei, YU Xingxing, et al. Energy-efficient resource allocation for cognitive radio networks[C]//IEEE.IEEE GLOBECOM.Atlanta:IEEE Press, 2013:1026-1031.

[10] GAO Yan, XU Wenjun, LI Shengyu, et al. Energy efficient resource allocation for cognitive radio networks with imperfect spectrum sensing[C]//IEEE.IEEE PIMRC. London: IEEE Press, 2013:3318-3322.

[11] OZCAN G, GURSOY M C. Energy-efficient power adaptation for cognitive radio systems under imperfect channel sensing[C]//IEEE.IEEE INFOCOM. Toronto:IEEE Press, 2014:706-711.

[12] ABDULRAHMAN A, ZOUHEIR R, BASEM S. Energy efficient resource allocation for cognitive radios: a generalized sensing analysis[J].IEEE Transactions on Communications,2015, 14(5):2455-2469.

[13] EBRAHIM B, OSAMA A, OCTAVIA A, et al. Energy-efficient power loading for OFDM-based cognitive radio systems with channel uncertainties[J].IEEE Transactions on Vehicular Technology, 2015,64(6):2672-2677.

[14] LI He,FENG Xinxin,GAN Xiaoying, et al. Joint spectrum sensing and transmission strategy for energy-efficient cognitive radio networks[C]//IEEE.The 8th International Conference on Cognitive Radio Oriented Wireless Networks. Washington: IEEE Press, 2013: 99-104.

[15] WU Xia,XU Jinling,CHEN Ming,et al.Joint optimization over sensing time and power allocation in cognitive radio networks based on energy efficiency[C]//IEEE.IEEE CHINACOM.Maoming:IEEE Press,2014:545-549.

[16] LI Xiaohui, CAO Jianlong, JI Qiong, et al. Energy efficient techniques with sensing time optimization in cognitive radio networks[C]//IEEE.IEEE WCNC. Shanghai: IEEE Press, 2013:25-28.

[17] SUN X, TSANG D H K. Energy-efficient cooperative sensing scheduling for multi-band cognitive radio networks[J]. IEEE Transactions on Wireless Communications,2013,12(10):4943-4955.

[18] ERYIGIT S,BAYHAN S,TUGCU T. Energy-efficient multichannel cooperative sensing scheduling with heterogeneous channel conditions for cognitive radio networks[J].IEEE Transactions on Vehicular Technology, 2013, 62(6): 2690-2699.

[19] ZHANG Tengyi,DANNY H K T. Cooperative sensing scheduling for energy-efficient cognitive radio networks[J].IEEE Transactions on Vehicular Technology,2015,64(6):2648-2662.

[20] XIONG Cong,LU Lu,LI G Y. Energy-efficient spectrum access in cognitive radios[J].IEEE Journal on Selected Areas in Communications, 2014, 32(3):550-562.

[21] ISHEDEN C,FETTWEIS G P. Energy-efficient multi-carrier link adaptation with sum rate-dependent circuit power[C]//IEEE.IEEE GLOBECOM. Miami:IEEE Press, 2010:1-6.

[22] CUI S,GOLDSMITH A J,BAHAI A. Energy-constrained modulation optimization[J].IEEE Transactions on Wireless Communications,2005, 4(5):2349-2360.

[23] WONG C Y,CHENG R S,LATAIEF K B, et al. Multiuser OFDM with adaptive subcarrier, bit, and power allocation[J]. IEEE Journal on Selected Areas in Communications,1999, 7(10):1747-1758.

[24] DINKELBACH W.On nonlinear fractional programming[J].Management Science, 1967, 13(7):492-498.

[25] BOYD S, VANDENBERGHE L. Convex optimization[M].UK:Cambridge University Press, 2004:24-125.

谢显中(1966-)，男，四川人，教授，博士，主要研究方向为MIMO预编码、认知无线电网络和协作通信。E-mail：xiexzh@cqupt.edu.cn。

肖正瑛(1988-)，男，重庆人，硕士，主要研究方向为认知无线电。E-mail：277699773@qq.com。

张森林(1989-)，男，重庆人，硕士，主要研究方向为干扰对齐。E-mail：254945521@qq.com。

(编辑：王敏琦)

s：The National Natural Science Foundation of China(61271259, 61301123); The Science and Technology Research Project of Chongqing Education Commission( KJ120501, KJ130536)

Study on optimization of energy consumption in cognitive multiple access system

XIE Xianzhong, XIAO Zhengying, ZHANG Senlin

(Institute of Personal Communications, Chongqing University of Posts and Telecommunications, Chongqing 400065, P.R.China)

The energy consumption is considered in cognitive multiple access system, which the channels are simultaneously shared by multiple secondary users and primary users. The multiple channels are sensed and accessed by secondary users at the same time and the interferences on primary users are kept within a certain range. Sensing time, channels and inter ference power are needed to be properly allocated for reducing energy consumption. Moreover, the interference power is served as constraint condition for protecting quality of service of primary users. The constructed initial optimizing problem is the non-convex integer combinatorial fractional programming issues in the multi-users multi-channels sensing-based spectrum sharing scheme. The concave relaxation is used to solve the issues which are further transformed the parametric linear problem for jointly optimizing sensing time, channels and power and an algorithm of minimizing energy consumption is proposed. Finally the impacts of the number of secondary users and channels and interference power on the energy consumption and optimal sensing time are discussed by simulations. Meanwhile the analysis is verified.

cognitive radio; multiple access; spectrum sharing; energy consumption

10.3979/j.issn.1673-825X.2016.05.008

2016-01-11

2016-09-07通讯作者：肖正瑛277699773@qq.com

国家自然科学基金(61271259, 61301123);重庆市教委科学技术研究项目(KJ120501, KJ130536)

TN925

A

1673-825X(2016)05-0658-09