基于激光干涉法的地表重力垂直梯度测量系统设计及试验*

吴　琼　滕云田　张　兵　郭有光

1) 中国北京100081中国地震局地球物理研究所2) 中国河北三河065201防灾科技学院



基于激光干涉法的地表重力垂直梯度测量系统设计及试验*

吴琼1),*滕云田1)张兵2)郭有光1)

1) 中国北京100081中国地震局地球物理研究所2) 中国河北三河065201防灾科技学院

基于激光干涉法对新型地表重力垂直梯度测量系统进行了研究并初步构建了原理样机． 该测量系统利用双光路干涉测量法，获取垂直向间距为50 cm且同步自由下落的两个落体相对于参考点的时间和位移信息，并通过差分运算得到该测点的重力垂直梯度值． 在系统设计过程中, 主要解决了双落体自由下落的同步自动控制和双干涉测量光路的垂直性调节问题． 试验结果表明，本套测量系统可以获取双落体同步自由下落运动时的干涉条纹信号，并完成重力垂直梯度测量，且梯度测量精度优于100 E．

重力梯度激光干涉测量落体控制

引言

高精度重力梯度测量作为一种新兴的地球物理探测技术，不仅在海洋重力辅助导航、海底潜艇探测和海底资源勘探等领域具有重要意义(徐遵义等，2007； DiFrancescoetal，2009； Arayaetal，2011)，而且在陆地资源勘探、大型水库监测和水底坑洞探测等领域也是一种有效的地球物理探测技术(王谦身，2003; Woolrychetal，2015)． 此外，航空和卫星重力梯度测量在地球重力场等基础科学研究领域也具有重要的作用(宁津生等，1996，2002)．

自1971年美国空军首次提出精度为1 E的移动级重力梯度仪以来，高精度重力梯度仪的研究得到了迅速发展，其主要设计原理为差分加速度计和扭矩测量． 基于差分加速度计的航空重力梯度仪, 由于其自身的高稳定性和高精度得到了迅速发展和应用(李红军等，2002； 刘凤鸣等，2009)，但大部分还处于实验样机阶段，目前唯一定型的商用重力梯度仪是美国贝尔实验室研制的旋转加速度计重力梯度仪(DiFrancescoetal，2009)． 基于扭矩测量的重力梯度仪, 由于体积和稳定性问题，其发展受到了限制． 彭益武等(2006)设计的基于扭矩测量的二维簧片重力梯度仪在体积和稳定性等方面取得了突破． 另外，超导重力梯度仪由于其测量精度、体积和整体质量等方面的优势，越来越多地被应用于航空重力测量中(吴琼等，2013)，具有非常好的发展前景(Moodyetal，2002)．

上述各类梯度仪的设计原理均属于相对测量，需要对参考坐标及变化的物理量进行标定，不适用于发射到宇宙外星球进行长期的内部质量分布探测研究，因此，在美国宇航局20世纪末的火星探测计划中，Micro-G公司开展了基于激光干涉原理的绝对重力梯度仪的研制，其测量精度的设计指标为1 E，其目的是探测火星的深部结构(Brownetal，1999; Robertson，2001)．

受此启发，激光绝对重力梯度仪作为研究地球深部质量迁移的一种新型有效工具，更能满足地震的监测需求． 目前，我国差分加速度计的最高精度为10-6m/s2，这与梯度仪要求的测量精度还有很大差距； 而现有的绝对重力测量技术的测量精度可达10-8m/s2，完全能够满足重力梯度仪的精度要求(胡华等，2012； 滕云田等，2013)，故基于创新设计及软件开发，利用激光干涉法完成地表重力垂直梯度测量的方案是完全可行的． 虽然目前该仪器的体积较大，但从固定台站观测的角度看，该缺点可以忽略； 而且随着激光干涉重力梯度仪研究的进一步开展，将来可以进行小型化设计，使之满足移动重力垂直梯度仪的测量需求．

本文拟基于激光干涉法对新型地表重力垂直梯度测量系统进行研究并初步构建原理样机. 该测量系统采用激光干涉原理，通过测定两个落体同步自由下落时相对于刚性连接的两个参考点的位置信息确定各自的重力加速度，然后通过差分计算得到测点的重力垂直梯度． 由于两个参考点为刚性连接，其感受到地面的振动信息完全相同，且两个落体利用同一套伺服控制系统，由振动引入的测量误差将在差分时消除，这样即可得到某测点的高精度重力垂直梯度值． 与其它重力梯度仪相比，激光干涉重力梯度仪具有以下优点： ① 有较大的测量范围，无需标定，无漂移； ② 地面振动属于共模误差，无需设计特殊的隔振系统，对动态测量非常有利； ③ 地面倾斜属于共模误差； ④ 对地球浅层异常质量体敏感．

1　设计原理

1.1基本原理

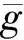
(1)

图1给出了重力梯度测量算法原理，主要是为了确定式(1)中的两个未知量href_U和href_D． 落体P1的初始位置为A00，其对应的初始速度和位移均为0，但在实际工作中一般将初始速度和位移无限接近于0的A0点作为其初始位置，在计算中近似认为A00与A0重合，因此hinst_U对应的是P1的初始位置． 在heff_U位置处，由于上落体P1在自由下落过程中所受到的重力梯度影响的综合效应为0，则测量得到的重力加速度值所对应的高度为

(2)

对于下落体P2，同样有

(3)

图1　重力梯度测量算法原理Fig.1　Principle for the algorithm of the gravity vertical gradient measurement

在计算重力垂直梯度时，首先计算heff_U和heff_D，然后将式(2)和(3)代入式(1)求得最终测点的垂直向重力梯度值． 对于heff_U和heff_D，二者采用的推导过程相同，这里仅以heff_U为例进行说明：

1) 设定初始条件． 考虑到重力垂直梯度的测量精度要求，在heff_U的计算过程中，其计算精度须精确到mm； 对于上落体P1，从初始位置A00到位置A0的下落运动过程为非自由下落运动，距离一般小于5 μm，时间小于30 ms． 这段非自由下落运动过程对heff_U值的影响在误差允许范围内，因此在计算中可被忽略． 也就是说，假设上落体在t00时刻从初始位置A00开始进入自由下落运动，则t0=0，v0=0，x0=0； 初始位置A00的绝对重力加速度g0为已知设定值． 此外，(t1，x1)和(tn，xn)已根据所获取的干涉信号解算得到．

2) 落体的自由下落运动方程为

(4)

根据假设的初始条件，解上述方程，可得

(5)

(6)

将式(5)代入式(6)，得

(7)

(8)

对比式(7)与式(8)，可得到

(9)

由式(9)可知，在利用同一套落体伺服控制系统对上、下落体进行同步控制的过程中，heff_U与heff_D在对应的开始时间t1和结束时间tn的取值完全相同，即heff_U=heff_D，故将式(2)和式(3)代入式(1)，得

(10)

即利用式(1)进行重力垂直梯度计算时与g0的选取无关，仅取决于上、下落体自由下落时重力加速度的计算和结构设计时所确定的两个落体光心之间的距离． 结构设计过程中，设上、下落体光心间的水平距离为95 mm，若水平梯度按300—500 E(朱英，李卢玲，1982)计算，梯度测量误差为3—5 E，而本套梯度测量系统精度为100 E，因此水平梯度引入的误差可以暂时忽略，故式(1)中上、下落体的光心间距即为上、下落体光心间的垂直距离．

1.2光路设计

激光干涉法重力垂直梯度测量系统的光路设计如图2所示． 可以看到，激光器发出激光束入射至分光镜BS1的上表面，分别得到BS1上表面透射和反射两束同源激光，透射光入射至分光镜BS2的上表面，反射光经反射镜M反射后入射至分光镜BS3上表面． 分光镜BS2、下落体P2和参考镜M2等构成下落体P2的干涉测量光路，所形成的干涉条纹利用雪崩光电二极管(advanced photo diodes，简写为APD，下文分别用APD1和APD2表示上落体P1和下落体P2自由下落时形成的干涉条纹的接收器)接收并转换为电压信号被后端的高速数字化仪接收； 分光镜BS3、上落体P1和参考镜M1等构成P1的干涉测量光路，形成的干涉条纹被APD1接收并转换为电压信号被后端的高速数字化仪接收(吴琼等，2011)．

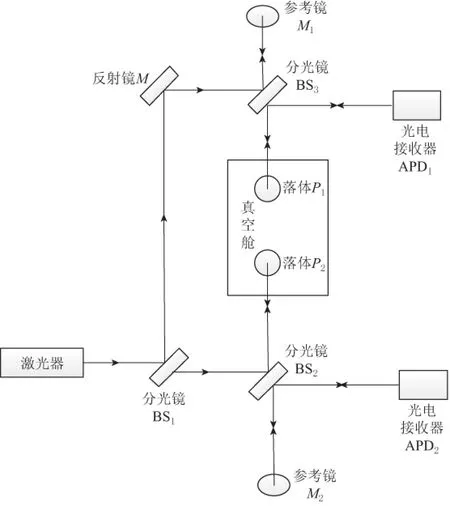
图2　干涉法重力梯度测量原理Fig.2　Measuring principle of the gravity vertical gradient based on interferometry

这套装置中，激光器、分光镜(BS1，BS2，BS3)、反射镜(M)、参考镜(M1，M2)和光电接收器(APD1，APD2)均为刚性连接，真空舱中的P1和P2在同一套伺服电机控制系统作用下作自由下落运动，因此APD1和APD2接收到的干涉条纹所受到的地震动、真空度、气压、极移和潮汐等环境干扰均保持相同． 源自这些因素的误差在测点重力梯度的差分计算时将被自动消除，不会影响最终测量结果的精度．

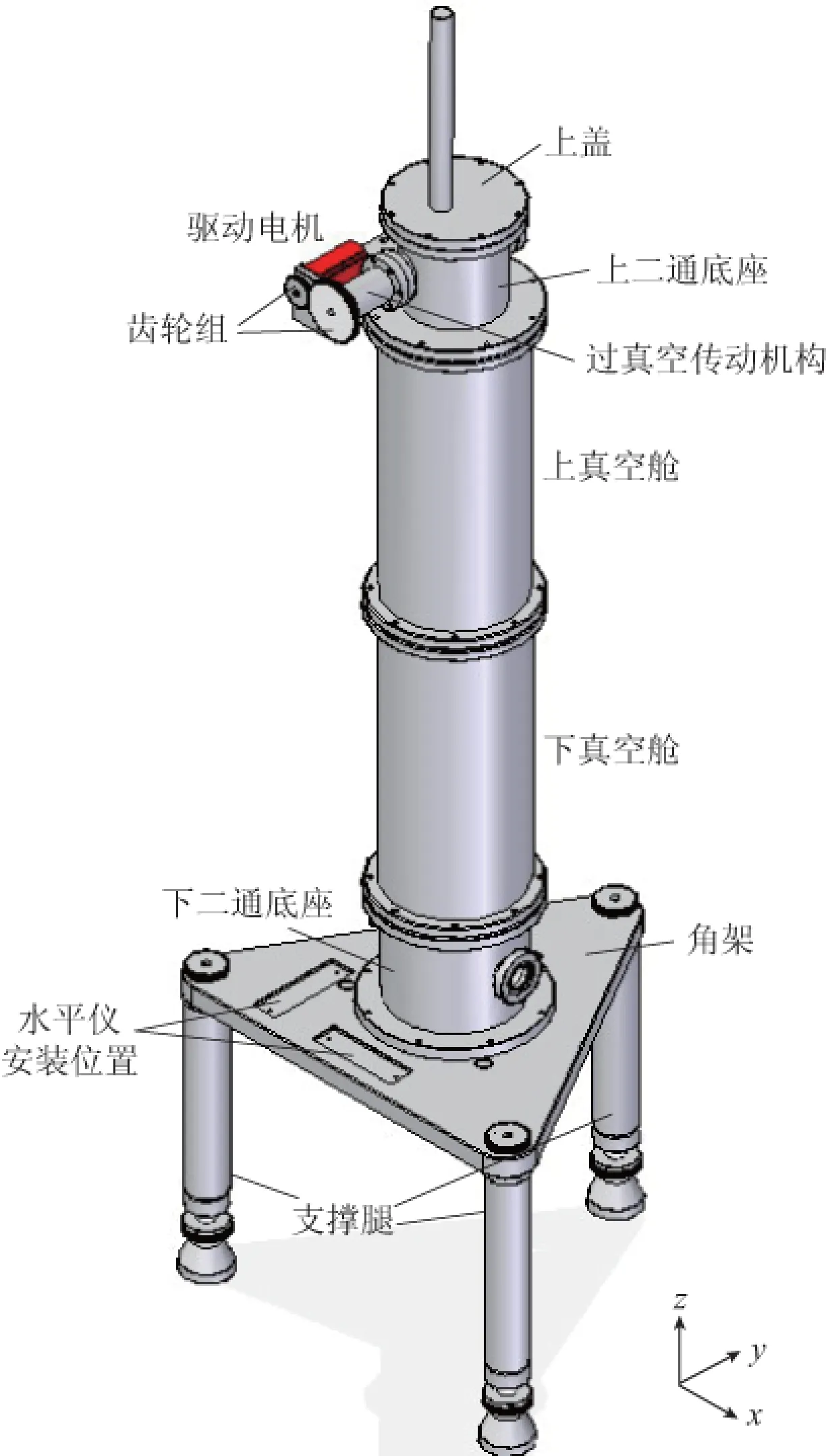
图3　真空系统设计Fig.3　Design for the vacuum system

2　测量系统设计

2.1双落体伺服控制系统结构设计

基于激光干涉法的重力垂直梯度测量系统是利用一套电机伺服控制系统控制垂直方向间距为50 cm的两个落体作同步自由下落运动，故需要构建一个如图3所示的真空系统，为落体的自由下落提供高真空环境，并为双落体伺服控制系统提供机械支撑．

真空系统安装在由3个支撑腿支撑的角架上，其中心旋转轴通过角架的质心，以确保角架完成水平调节后，真空系统的中心旋转轴为竖直状态． 该系统由上盖、上二通底座、上真空舱、下真空舱和下二通底座等构成． 由于真空系统腔体较大，在构建真空环境时将分子泵直接安装在下二通底座上，并将其预抽至2×10-4Pa以上时打开离子泵阀门，维持真空腔体内真空度优于5×10-4Pa，满足落体自由下落对真空度的要求．

图4为图3所示真空系统内部安装的落体伺服控制系统． 图4a显示的是落体伺服控制系统的整体结构，电机的输出力矩通过大气侧齿轮组和过真空传动机构驱动真空侧的齿条带动双落体作上下往复运动； 齿条经齿条运动导座约束后，可确保其沿竖直方向上下运动． 上托架内放置上落体P1，齿条通过万向联轴节驱动上托架，上托架沿上导轨作上下往复运动，对于下落体P2的驱动也采用同样的控制方式． 图4b所示结构是为保证上、下落体驱动的同步性而进行的特殊设计，由连接板、连接块、连接柱以及万向联轴节等构成． 连接板通过4个螺钉与上托架底端固定，末端与连接块固定； 连接块通过螺母锁定连接柱，三者构成“7”型结构； 连接柱通过万向联轴节与下托架固定． 该设计不仅可以保证上、下托架在电机驱动下同步运动，还可抵消安装误差和制造误差所造成的径向力作用，使整套控制机构运行平稳可靠．

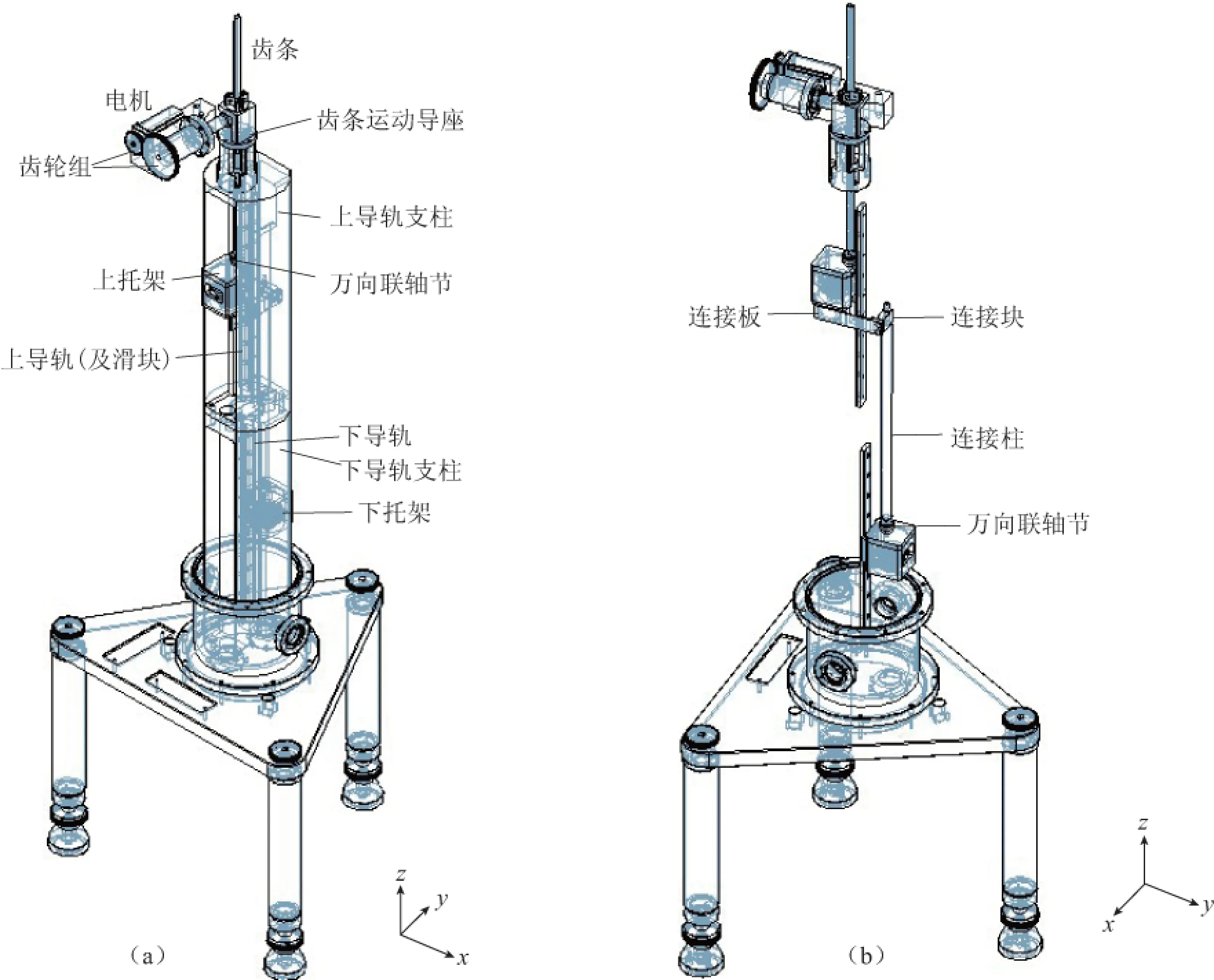
图4　落体伺服控制系统设计(a) 安装在真空舱内的落体伺服控制系统设计； (b) 上、下落体间刚性连接机构设计Fig.4　Design of the free-fall body servo control mechanism(a) Design of the free-fall body servo control mechanism in vacuum chamber; (b) Design of the rigid linkage between the up and down free-fall bodies

2.2双光路干涉测量系统设计

双光路干涉测量系统首先通过两个干涉光路测量单元分别采集上落体和下落体在自由下落过程中形成的激光干涉信号，再通过对其解算和差分运算得到地表重力垂直梯度．

依据图2所示的测量原理设计双光路干涉测量系统的机械结构，如图5所示． 激光器采用碘稳频激光系统，波长稳定度可达10-12，为整套测量系统提供长度基准． 高速数字化仪的时间基准由外部铷原子时钟提供，铷原子时钟输出频率的稳定度可达10-11，为整套仪器提供时间基准．

干涉条纹的处理解算方面，由于上、下落体自由下落的时间和位移信息可追溯到时间和长度基准，所以最后通过差分获得的重力垂直梯度值就具有了大动态范围、无需标定和无零漂等特点； 构成双光路干涉测量系统所需的各个部件均刚性安装在双光路干涉测量系统的底板上，因此振动产生的误差属于共模误差，不会对最终的梯度测量结果产生影响．

图5　双光路激光干涉测量系统机构设计Fig.5　Design of the measuring structure of dual optical path measuring system based on laser interferometry

光束垂直性调节方面，与激光干涉绝对重力仪不同，双光路干涉测量系统需要对两条测量光束进行垂直性调节． 首先，利用酒精液面提供的水平面和光学自准直仪，通过调整双光路干涉测量系统底板的支撑腿，调整入射上落体P1的测量光束的垂直性； 然后，同样利用酒精液面提供的水平面和光学自准直仪，通过调整反射镜M上的微调螺母，调整入射下落体P2的测量光束的垂直性． 这种调整方案的误差与光学自准直仪的误差相同，可以保证入射落体P1和P2的测量光束的垂直性误差小于0.2″．

2.3测量系统构建与初步试验

目前，根据2.1和2.2节的设计已构建完成了一套可以正常工作的激光干涉法地表重力垂直梯度测量系统，如图6a所示． 由于这套测量系统机构比较庞大，目前仅在实验室获取了初步的试验数据，如图6b所示． 试验数据共有35组，每组进行16次测量.

图6　激光干涉法地表重力垂直梯度测量系统(a)及其初步试验数据(b)Fig.6　The apparatus of the gravity vertical gradient measurement based on laser interferometry (a)and its preliminary test data (35 groups and 16 measurements per group) (b)

在落体自由下落过程中，选取0.045—0.130 s时段的干涉信号进行计算． 对应落体自由下落距离为1—8 cm，生成的干涉信号是调频正弦波，频率为1.4—4.0 MHz(吴琼等，2012)． 考虑到采样频率引入的时间测量误差，选取采样频率为100 MHz，使得由采样引入的时间误差导致最终的测量误差小于1×10-8m/s2．

图7给出了单次测量中上落体自由下落时生成的干涉信号及其展开，可以看出，获取的干涉信号无明显干扰信号，信噪比高，可以满足高精度重力加速度值计算的要求．

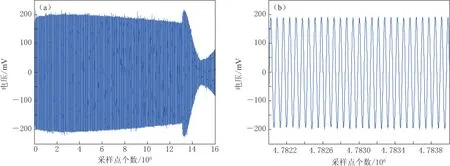
图7　实测上落体自由下落时得到的干涉条纹(a)及其展开(b)Fig.7　The interference fringes of the upper free-fall body during freely falling (a)and the expansion of the part of these fringes (b)

3　讨论与结论

在重力垂直梯度的测量过程中，潮汐、极移、气压、真空度、温度梯度、涡流以及参考棱镜的振动等相较于明显的误差源，在绝对重力测量时不会影响重力垂直梯度的测量结果，但双落体自由下落的同步性控制、参考点以及各个光学部件间的刚性和双测量光路的垂直性等则是影响其测量精度的重要因素．

2012年至今，在原有设计研发激光干涉重力仪的基础上，初步完成了激光干涉法地表重力垂直梯度测量系统的原理研究、结构设计和系统构建等，并获取了本套测量系统的第一批试验数据． 从图7所示的干涉信号可以看出，本套测量系统获取的上、下落体在自由下落过程中所产生的干涉信号的信噪比高，干涉条纹清晰完整、无畸变，完全满足后期的计算要求． 图6b显示的是本次试验完成的35组测量结果的组平均值，试验中每组设定的测量次数为16次，共完成560次测量． 对测量获得的35组平均值再进行求平均计算，确定本次试验样机测量的测点的垂直向重力梯度为2886 E，精度为99 E．

2012年11月曾利用两台拉科斯特相对重力仪对本次试验所在测点的重力垂直梯度进行测量，得到的梯度值为2402 E(精度100 E)，对比分析初步确定本套梯度测量系统的测量准确度约为400 E．

本套梯度测量系统的精度和准确度不仅需要更多试验数据的测定，还需要制定更完备的测试精度和准确度的试验方案． 另外，针对伺服控制系统运行过程中的降噪问题、数据处理算法和整套仪器的小型化设计等方面尚需进一步改进．

胡华，伍康，申磊，李刚，王力军. 2012. 新型高精度绝对重力仪[J]. 物理学报，61(9): 099101.

Hu H，Wu K，Shen L，Li G，Wang L J. 2012. A new high precision absolute gravimeter[J].ActaPhysicaSinica，61(9): 099101 (in Chinese).

李红军，邓方林，柯熙政. 2002. 旋转加速度计重力梯度仪原理及其应用[J]. 地球物理学进展，17(4): 614--619.

Li H J，Deng F L，Ke X Z. 2002. Rotating accelerometer gravity gradiometer’s measurement principle and it’s applications[J].ProgressinGeophysics，17(4): 614--619 (in Chinese).

刘凤鸣，赵琳，王建敏. 2009. 基于加速度计重力梯度仪分析与设计[J]. 地球物理学进展，24(6): 2058--2062.

Liu F M，Zhao L，Wang J M. 2009. The design and analysis for the accelerometer-based gravity gradiometer[J].ProgressinGeophysics，24(6): 2058--2062 (in Chinese).

宁津生，罗志才，晁定波. 1996. 卫星重力梯度测量的研究现状及其在物理大地测量中的应用前景[J]. 武汉测绘科技大学学报，21(4): 309--314.

Ning J S，Luo Z C，Chao D B. 1996. The present situation on satellite gravity gradiometry and its vistas in the application of physical geodesy[J].JournalofWuhanTechnicalUniversityofSurveyingandMapping，21(4): 309--314 (in Chinese).

宁津生，罗志才，陈永奇. 2002. 卫星重力梯度数据用于精化地球重力场的研究[J]. 中国工程科学，4(7): 23--28.

Ning J S，Luo Z C，Chen Y Q. 2002. Application of satellite gravity gradiometry data to the refinement of the earth’s gravity field[J].EngineeringSciences，4(7): 23--28 (in Chinese).

彭益武，赵立珍，屈少波，周泽兵. 2006. 二维簧片重力梯度仪的研制[J]. 物探与化探，30(5): 401--405，409.

Peng Y W，Zhao L Z，Qu S B，Zhou Z B. 2006. The research and development of a two-dimensional flexure hinge gradio-meter[J].Geophysical&GeochemicalExploration，30(5): 401--405，409 (in Chinese).

滕云田，吴琼，郭有光，张兵，张涛. 2013. 基于激光干涉的新型高精度绝对重力仪[J]. 地球物理学进展，28(4): 2141--2147.

Teng Y T，Wu Q，Guo Y G，Zhang B，Zhang T. 2013. New type of high-precision absolute gravimeter base on laser interference[J].ProgressinGeophysics，28(4): 2141--2147 (in Chinese).

王谦身. 2003. 重力学[M]. 北京: 地震出版社: 291--294.

Wang Q S. 2003.Gravitology[M]. Beijing: Seismological Press: 291--294 (in Chinese).

吴琼，滕云田，郭有光. 2011. 激光干涉重力梯度仪设计方案[J]. 物探与化探，35(2): 230--233.

Wu Q，Teng Y T，Guo Y G. 2011. The scheme for designing the laser interferometer gravity gradiometer[J].Geophy-sical&GeochemicalExploration，35(2): 230--233 (in Chinese).

吴琼，滕云田，黄大伦，龙剑锋. 2012. 绝对重力仪研制中一种新的自由落体轨迹重建算法[J]. 地震学报，34(4): 549--556.

Wu Q，Teng Y T，Huang D L，Long J F. 2012. A new type of algorithm for rebuilding the trace of free-fall body in absolute gravimeter development[J].ActaSeismologicaSinica，34(4): 549--556 (in Chinese).

吴琼，滕云田，张兵，张涛. 2013. 世界重力梯度仪的研究现状[J]. 物探与化探，37(5): 761--768.

Wu Q，Teng Y T，Zhang B，Zhang T. 2013. The research situation of the gradiometer in the world[J].Geophysical&GeochemicalExploration，37(5): 761--768 (in Chinese).

徐遵义，晏磊，宁书年，邹华胜. 2007. 海洋重力辅助导航的研究现状与发展[J]. 地球物理学进展，22(1): 104--111.

Xu Z Y，Yan L，Ning S N，Zou H S. 2007. Situation and development of marine gravity aided navigation system[J].ProgressinGeophysics，22(1): 104--111 (in Chinese).

朱英，李卢玲. 1982. 利用重力水平梯度Δgx计算深度的方法及地质效果[J]. 石油物探，(3): 1--16.

Zhu Y，Li L L. 1982. An approach of calculating the depth from horizontal gravity gradient (Δgx) and its geological reasoning[J].GeophysicalProspectingforPetroleum，(3): 1--16 (in Chinese).

Araya A，Kanazawa T，Shinohara M，Yamada T，Fujimoto H，Iizasa K，Ishihara T. 2011. A gravity gradiometer to search for submarine ore deposits[C]∥2011IEEESymposiumonand2011WorkshoponScientificUseofSub-marineCablesandRelatedTechnologies:UnderwaterTechnology.Tokyo: IEEE: 1--3.

Brown J M，Niebauer T M，Klopping F J. 1999. Results from a new interferometric ballistic differential gravity meter[J].BollGeofisTeorAppl，40(3): 487--496.

DiFrancesco D，Grierson A，Kaputa D，Meyer T. 2009. Gravity gradiometer systems: Advances and challenges[J].GeophysProsp，57(4): 615--623.

Moody M V，Paik H J，Canavan E R. 2002. Three-axis superconducting gravity gradiometer for sensitive gravity experiments[J].RevSciInstr，73(11): 3957--3974.Robertson D S. 2001. Using absolute gravimeter data to determine vertical gravity gradients[J].Metrologia，38(2): 147--153.

Woolrych T R H，Christensen A N，McGill D L，Whiting T. 2015. Geophysical methods used in the discovery of the Kitumba iron oxide copper gold deposit[J].Interpretation，3(2): SL15--SL25.

Development and experiments of the gravity vertical gradient measuring system based on the laser interferometry

Wu Qiong1),*Teng Yuntian1)Zhang Bing2)Guo Youguang1)

1)InstituteofGeophysics，ChinaEarthquakeAdministration，Beijing100081，China2)InstituteofDisasterPrevention，HebeiSanhe065201，China

This paper develops a new apparatus for measuring the vertical gravity gradient based on the laser interferometry. The apparatus uses the method of dual optical interferometer to determine the time shifting coordinates of dual free-fall bodies spaced 50 cm vertically，and then calculates the gravity gradient by using differential algorithm. In design and development of this instrument，particular attention is paid to those aspects which would affect synchronistically automatic control of the free-fall bodies and vertical adjustment of the dual measuring beams. The results of the experiments show that the apparatus can obtain the interference signals of these two free-fall bodies during the freely falling and complete the measurement of the gravity gradient with accuracy better than 100 E.

gravity gradient; laser interferometry; falling-body controlling

国家科技支撑计划(2012BAF14B12)资助.

2016-02-23收到初稿，2016-04-25决定采用修改稿.

e-mail: wuqiong@cea-igp.ac.cn

10.11939/jass.2016.05.013

P315.62

A

吴琼, 滕云田, 张兵, 郭有光. 2016. 基于激光干涉法的地表重力垂直梯度测量系统设计及试验. 地震学报, 38(5): 794--802. doi:10.11939/jass.2016.05.013.

Wu Q, Teng Y T, Zhang B, Guo Y G. 2016. Development and experiments of the gravity vertical gradient measuring system based on the laser interferometry.ActaSeismologicaSinica, 38(5): 794--802. doi:10.11939/jass.2016.05.013.