加劲十字形轴压杆考虑初始扭转缺陷的扭转位移函数

陈行威，宋振森

(上海交通 大学土木工程系，上海200240)



加劲十字形轴压杆考虑初始扭转缺陷的扭转位移函数

陈行威，宋振森

(上海交通 大学土木工程系，上海200240)

在小变形假定下推导了加劲十字形轴压杆考虑初始的扭转位移函数解，讨论了解的形态及其统一表达式，并与有限元进行了对比验证。分析表明，理论解与有限元结果吻合较好，当轴力小于0.4Afy时两者基本没有误差；轴力与构件跨中的扭转位移之间存在明显的二阶效应，跨中扭转位移的增加率随轴力的增加而增加；初始扭转缺陷对加劲十字形轴压杆有不利影响，其影响程度与其幅值基本呈线性关系。

加劲十字形截面;轴心受压构件;扭转失稳;位移函数

近年来，随着建筑美观和施工效率要求的提高，建筑中钢结构异形构件的使用率逐渐提高，其中，由两个标准工字钢切割焊接而成的加劲十字形截面构件使用最为广泛。相对于一般类型截面的构件，加劲十字形截面构件具有许多优势。例如，从建筑美观的角度来看，普通截面框架柱在框架结构中容易产生室内凸角，对建筑的美观性有一定的影响，采用加劲十字形截面柱取代普通截面框架柱作为竖向支撑构件则能够有效地解决这一问题[1]。另外，在受力性能方面，该类截面在各个方向的抗弯刚度相等，不存在弯曲弱轴，易于实现各个弯曲方向的等稳定设计。再者，从施工安装的角度来看，附加的翼缘为该类构件提供了更多的连接面，方便构件间的螺栓连接和焊接，能够有效缩短安装时间，减少劳动工作日[2]。

目前关于加劲十字形截面构件的研究较少，且大多集中在数值模拟和初步的实验探究阶段。例如，Tahir, M. M.和Shek, P. N.[3]对长细比在26～35之间的四组加劲十字形截面轴心受压构件和常规工字型截面轴心受压构件进行了对比实验。Ngian, S. P.等[4]分别利用传统工字型截面构件和带翼缘十字型截面构件对一个8层的无支撑半刚性钢框架按照WMM(wind-moment method)法进行了设计对比。Naderian, H. R.等[5]利用有限条法对FRP材料组成的加劲十字形截面轴心受压构件进行了数值分析。于劲[6]通过数值模拟和实验研究了该类构件的滞回性能。李正超[7]利用数值模拟研究了初始扭转对加劲十字形截面构件的稳定性影响。在已有的少量关于加劲十字形截面构件的文献中，均未见到对该类构件的基本力学性能的研究报道。实验现象表明，加劲十字形轴压杆极易出现扭转失稳。本文从薄壁构件的符拉索夫理论出发，研究初始扭转影响下构件的扭转位移，并结合有限元方法对所推导出的扭转位移函数解进行对比验证，为该类构件的后续研究提供一定的理论指导。

1.扭转位移函数

1.1扭转平衡微分方程

对于加劲十字形截面轴压杆而言，其发生扭转失稳时的扭转位移函数可以通过以下扭转平衡方程式单独确定。

Mt+Mω=MG

(1)

其中Mt=GItφ′为自由扭转扭矩，Mω=-EIωφ‴为翘曲扭矩，MG为轴压力的Wagner效应产生的扭矩。

(2)

对全截面积分可以得到初始扭转的Wagner效应所产生的扭矩为

(3)

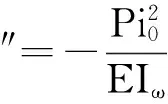
(4)

若考虑初始缺陷为幅值Aφ位于移构件跨中的正弦函数φ0(z)=Aφsin(πz/L)有

(5)

由于加劲轴压杆通常作为结构柱使用，构件的端部通常不允许扭转和翘曲，因此可取端部的边界条件为扭转固接，即

φ(0)=φ(L)=φ′(0)=φ′(L)=0

(6)

1.2扭转位移函数解

(1)当ξ2>0时，式( 5)的通解为

(7)

(8)

(2)当ξ2=0时，此时扭转平衡微分方程可化为

(9)

此时扭转微分方程的解为

(10)

(11)

(12)

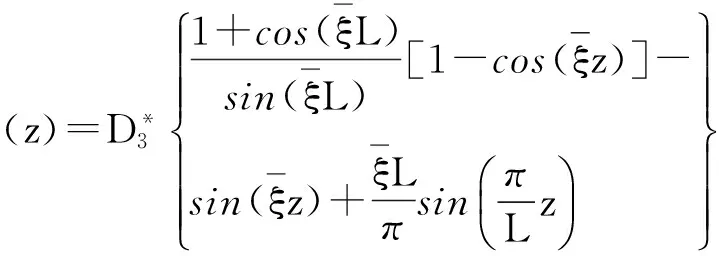
(13)

1.3扭转位移函数解的统一表达

式( 5)的求解是分别在ξ2>0，ξ2=0和ξ2<0时的情况下进行的，实际上，根据复变函数的理论，三种情况下的解可以统一为ξ2>0或ξ2<0时的解。下面以ξ2>0时的解式( 8 )为统一表达式推导ξ2=0和ξ2<0时的解。

当ξ2=0时，使用Hospital法则考虑ξ2→0时有

(14)

=φ(z)|ξ<0

(15)

因此，ξ2<0时的解也可以用ξ2>0时的解来表示，故后续对于解的讨论均可以从式( 8 )入手。

2　有限元对比分析

为进一步验证扭考虑初始扭转缺陷的扭转位移函数解，本文通过大型通用有限元软件ANSYS对加劲十字形轴压杆进行了数值模拟对比分析。算例采用常见截面H248×124×5×8，构件长度取为3000mm，材料属性取Young′s模量为E=2.06×105N/mm2，剪切模量取为G=E/2.6=79 230N/mm2。

2.1模型概况

采用壳单元shell181对加劲十字形轴压杆进行模拟。模型中单元尺寸取为腹板的厚度5mm，经试算该单元尺寸已具有很高的精度。划分好网格的整体模型如图 2所示。

由于扭转简支边界条件下轴压杆的扭转位移函数为式( 16 )所示的正弦曲线[8]，因此正弦分布的初始扭转缺陷可以通过求解扭转简支边界条件下的失稳模态来构造。

φ(z)=Csinξz

(16)

实际计算时的边界条件为扭转固接。在扭转固接的条件下，构件的端部即不允许转动也不允许翘曲，为了对端部所有节点翘曲方向的自由度进行耦合，在构件的两端分别建立了位于构件之外，但Z向投影与截面形心重合的间接加载点和间接约束点。并如图3所示，通过解析刚体单元MPC184将两端的所有节点分别与间接加载点和间接约束点相连。

2.2分析结果及对比

利用建立的考虑了初始扭转缺陷的有限元模型，分别计算了构件跨中初始扭转角为50和100两种情况下，轴力在0.2Afy～0.8Afy范围内加劲十字形截面轴压杆的受力情况。

将扭转位移的有限元结果与理论解进行对比，并将对比结果汇总于图4-图5。由图可知，有限元计算得出扭转位移曲线与理论解的曲线形态基本吻合，当荷载较小时有限元结果与理论解的误差较小，当轴力P=0.4Afy时有限元的计算结果基本上与理论解一致，可见当轴力P在0.4Afy附近时理论解中的小变形假定较为符合实际情况。随着荷载的增大，理论解与有限元小变形计算结果的偏差逐渐增大，但始终介于大变形和小变形的计算结果之间，可见随着荷载的增大，理论模型中小变形假定所造成的误差会逐渐增大。

图6汇总了构件跨中扭转角的有限元结果与理论解的对比。由图可见，构件跨中的扭转位移随轴力的增大而增大，但两者并不是简单的线性关系，曲线的斜率会随着轴力的增加而不断提高，这是由于轴力的增加会使得扭转角增大，而扭转角的增大又会反过来导致Wagner效应增大，加剧扭转，可见在扭转问题上也存在明显的P～δ效应。另外，图6再次说明了荷载的增大会使得小变形假设下的理论解与有限元解的误差增大，但理论解始终介于有限元小变形解和大变形解之间，而当荷载较小时，三者基本相等，此时可认为理论分析中的小变形假定是合理的。

3　结论

1)加劲十字形轴压杆考虑初始扭转的扭转位移函数在解的性态上与有限元计算的结果一致，当轴力小于0.4Afy时，由于小变形假定带来影响可以忽略不计，此时理论解与有限元大变形和小变形的计算结果基本相等。

2)初始扭转缺陷对于加劲十字形轴压杆而言十分不利，当轴压力一定时，初始扭转角越大，则构件跨中的扭转位移就越大，且初始扭转角构件跨中的扭转位移基本呈正相关关系。

3)轴力与构件跨中的扭转位移之间存在明显的P～δ效应，随着轴力的增大，构件跨中扭转位移的增长率也不断提高。轴力的增加会使得扭转角增大，而扭转角的增大又会反过来导致Wagner效应增大，加剧扭转。

[1]张爱林，于 劲，徐 敏，等.钢异形柱结构体系的发展前景和研究计划[C]//庆祝刘锡良教授八十华诞暨第八届全国现代结构工程学术研讨会.2008.中国天津.

[2]黄慧娟，王元清，麻建锁，等.钢结构工程住宅设计及其经济性分析[J].河北工程大学学报:自然科学版，2007,24(1):20-23.

[3]TAHIR M M.Experimental investigation of short cruciform columns using universal beam sections[J].Construction and Building Materials, 2009,23(3):1354-1364.

[4]NGIAN S P.Wind-moment design of semi-rigid un-braced steel frames using cruciform column (CCUB) section[J].International Journal of Steel Structures, 2015,15(1):115-124.

[5]NADERIAN H R,RONAGH，AZHARI M.Torsional and flexural buckling of composite FRP columns with cruciform sections considering local instabilities[J].Composite Structures, 2011, 93(10):2575-2586.

[6]于 劲. 钢异形柱结构体系抗震性能的理论分析与试验研究[D].北京：北京工业大学,2010.

[7]李正超.初始扭转对十字形截面压杆稳定性能的影响研究[D].苏州：苏州科技学院,2014.

[8]陈骥,钢结构稳定理论与设计[M].第4版.北京:科学出版社,2008.

(责任编辑李军)

The torsional displacement function of centrally compressed stiffened cruciform column with initially twisted imperfection

CHEN Xingwei,SONG Zhensen

(Department of Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China)

Based on the assumption of small deformation, this paper derives The torsional displacement function of centrally compressed stiffened cruciform column with initially twisted imperfection, gives its unified forms and discuss its property. A finite element model is developed and verified against the theoretical result. The study shows that results of FEM were generally in good agreement with the theoretical results when axial force is smaller then 0.4Afy. The is obvious second-order effect between axial force and torsional displacement. The initially twisted imperfection has negative effect on the centrally compressed stiffened cruciform column, and the degree of the influence has positive correlation with its amplitute.

Stiffened cruciform columns，Centrally compressed member，Torsional buckling.

2016-04-27

国家自然科学基金资助项目(51278296)

陈行威(1990-)，男，海南海口人，硕士，从事钢结构稳定方面研究。

1673-9469(2016)03-0008-05

10.3969/j.issn.1673-9469.2016.03.002

TU32

A