基于拓扑配准的甲骨文字形识别方法*

顾绍通

(江苏师范大学语言科学与艺术学院　徐州　221009)



基于拓扑配准的甲骨文字形识别方法*

顾绍通

(江苏师范大学语言科学与艺术学院徐州221009)

甲骨文字形具备较为稳定的拓扑结构特征,虽然异体字较多,但是同一字形的不同写法具有一定的拓扑稳定性,这使得从字形上区分不同的甲骨文字形成为可能。文章通过分析甲骨文字形的拓扑特征,研究甲骨文字形的拓扑顶点及拓扑顶点之间的拓扑关系,建立了拓扑顶点间拓扑关系的拓扑描述,将图画性质的甲骨文字形转化为拓扑图形,并对拓扑图形进行编码,实现了甲骨文字形拓扑结构的形式化描述。

拓扑配准; 拓扑结构; 拓扑顶点; 拓扑关系; 拓扑编码; 甲骨文; 字形识别

Class NumberTP391

1　引言

甲骨文是书写在龟甲和兽骨上的文字,是我国迄今发现的最早的一种成熟文字系统。出土甲骨拓片上的甲骨文字形中,大部分字形无法正确辨识其读音和意义,已有的甲骨文编码输入方法存在规则繁琐、重码多、效率低的局限[1～3],要让一般用户掌握其复杂的规则并不现实,只有少数从事甲骨文研究方面的专家学者才能掌握复杂的编码规则,因而实用性并不强。对于现代汉字已出现多种识别方法,大致可分为基于结构模式的方法和基于统计模式的方法。基于结构模式的识别方法,如隐马尔科夫模型[4]等,基于统计模式的识别方法,如贝叶斯决策的分类方法[5]等。这些方法都是针对现代汉字特点提出的识别方法,对于和现代汉字具有巨大差别的甲骨文字形识别适应性存在局限性。甲骨文是刻写在龟甲和兽骨上的文字,其构成方式主要有象形、指事、形声、会意等四种,其中象形字占大多数,这就决定了大多数甲骨文字形具有图画性,即使是一些会意字、形声字也是以象形字为基础,大都具有图画性,这也决定了甲骨文笔画繁多、构造复杂的特点；同时甲骨文的字形刚劲有力,笔端尖细,难以区分笔画,只能作为一个整体进行处理。针对甲骨文字形本身的特点,目前,已有学者已提出甲骨文字形的识别方法,如周新伦(1996)[6]提出利用图论和笔划特点来识别甲骨文字形的方法,李锋(1996)[7]提出利用图特征的原理来识别甲骨文字形的方法；利用图特征来识别甲骨文取得了不错的效果。栗青生(2011)等[8]提出利用图同构的方法来识别甲骨文字形,这种方法对于那些甲骨文中不同构但是仍为同一字形的异写字的识别没有进行处理,而且虽然同构但是却不是同一个字形的情况大量存在,这种算法的鲁棒性很低,因而实用性受到限制。

甲骨文的特色不仅在于是我国最早的成熟的文字系统以及它独特的书写材料,还在于它形成了中国文字体系结构的雏形。由于书写材料的质地坚硬、甲骨文创制人员的复杂,使得甲骨文字形的形态变化多样,具体表现在一个甲骨文字形不同的人有多种不同的刻写方法,不同的契刻方法造就了不同的甲骨文形体,有些形体之间差别还很大。但是如果仔细观察这些不同形体的甲骨文字形就会发现,不同形体之间虽然笔画顺序以及组合关系不同,但是它们之间的大体结构却是相似的,现代的学者能将不同形体的甲骨文字形归为一类,很大的原因在于字形之间结构的相似性,也就是同一甲骨文字形的不同形体之间在拓扑结构上具有同一性。本文将考察甲骨文字形拓扑结构的特点,并将甲骨文字形的拓扑特征形式化,从拓扑特征上寻求识别甲骨文字形的方法。

本文将首先分析甲骨文字形的拓扑顶点及拓扑顶点之间的拓扑关系,建立甲骨文字形的拓扑描述,构造甲骨文字形的拓扑图形(从字形抽象出来的的拓扑顶点之间连结构成的图形),将图画性质的甲骨文字形转化为拓扑图形；然后对甲骨文字形的拓扑图形进行编码,通过对甲骨文字形的拓扑编码与通用甲骨文字库中字形的拓扑特征库进行配准,实现甲骨文字形的识别。

2　甲骨文字形结构的拓扑表达

2.1拓扑学的一般知识

拓扑学最初是几何学的一个分支,是从图论演变过来的。拓扑学将实体抽象成与其大小、形状无关的点,将连接实体的线路抽象成线,进而研究点、线、面之间的关系。简单地说,拓扑学主要研究几何图形在连续变形下保持不变的性质,现在已成为研究连续性现象的重要的数学分支。直线上的点和线的结合关系、顺序关系,在拓扑变换下不变,这是拓扑性质。

设X和Y是拓扑空间,如果f:x→y是一一映射,并且f及其逆g:y→x都是连续的,则称f是一个拓扑变换,或称同胚映射。 当存在x到y的拓扑变换时,称x与y拓扑等价,或称同胚,记作X≅Y。例如图1中的各图形虽然形状各异,但是它们仍然是拓扑等价的。

图1　 拓扑等价示意图

拓扑不变量是拓扑空间一个比较重要的拓扑性质,它描述了弹性变化,如拉伸、旋转和缩放等条件下不变的性质。

拓扑学中比较简单的拓扑不变量有：

1)连通性及连通支的个数。从直观上来说,连在一起的图形是连通的,如果图形是由几个不相连接的部分组成的,则图形是不连通的,组成图形的互不连接的部分的数目称为连通支的个数。连通支的个数是1时,图形是连通的。连通支的个数是一个拓扑不变量。

2)割点的个数。在一个图形上有这样的点,去掉该点后,余下的是一个不连通的图形,具有这种性质的点,称为图形的割点。“割点”的概念是一个拓扑性质,割点在同胚映射下的象点仍然是割点。因而,割点的个数是一个拓扑不变量。

3)点的指数。设一个图形是由有限条弧组成的,x是这个图形的点,从x点引出的该图形的弧的个数,叫做点x在该图形中的指数。

对于给定的两个拓扑空间X与Y,如果要证明它们是拓扑等价的,只需要构造出从X到Y的同胚映射即可。若要证明给定的两个拓扑空间是不同胚的,可以通过寻找拓扑不变量,如果这两个拓扑空间的拓扑不变量是不相同的,那么就可以认为这两个拓扑空间是不同胚的,即拓扑不等价。

由此可见,证明两个图形同胚,需要找出同胚映射,或者借助于橡皮变形能将一个变成另一个。如果两个图形是同胚的,那么这两个图形就是拓扑等价的,即拓扑结构是相同的。

2.2甲骨文字形的拓扑顶点

字形是指构成每一个方块汉字的二维平面图形。构成汉字拓扑空间的要素是笔画及其位置关系。笔画是构成汉字字形的最小连笔单位,落笔处为笔画的起点,提笔处为笔画的终点。直线上的点和线的结合关系、顺序关系,在拓扑变换下不变,这是拓扑性质。甲骨文作为汉字的一种早期形态,从本质上来说,是一种平面图形,层次性不强,存在构形复杂,异写字、异构字繁多等特点,比如“犬”在甲骨文中的形态有一百多种。但是,我们仍然能够认知这一百多个不同形态的“犬”字,正是因为甲骨文具备了拓扑结构不变性的特征。判断两个甲骨文字形是否在拓扑上等价,可以转化为判断两个甲骨文字形在拓扑上能否配准。

图2是甲骨文字形“贞”的图像,图3是经过细化处理后的图像。甲骨文笔划线条相交的地方形成交点,甲骨文笔划的交点和字形笔划的端点统称为顶点。如图4所示。从图4可以看出,甲骨文字形的拓扑顶点是指笔划线条的交点以及甲骨文字形笔划的端点。甲骨文字形经过细化处理后,成为由细线条连接而成的图形。根据周新伦等(1996)[6]的研究,在目前已考证出的甲骨文字形中,指数高于6的顶点尚未发现。因而,甲骨文字形的拓扑顶点可以分为以下7类：孤立点、端点、二叉点、三叉点、四叉点、五叉点和六叉点。孤立点是甲骨文字形拓扑图形中指数为0的顶点,即没有边与之连接,端点是甲骨文字形拓扑图形中指数为1的顶点,二叉点是甲骨文字形拓扑图形中指数为2的顶点,三叉点、四叉点、五叉点、六叉点依此类推。从指数上看,甲骨文字形的顶点有7类,由排列组合关系知,甲骨文字形中两个顶点之间的连接关系可达7+6+5+4+3+2+1=28种。图4中标号1、5、7、10、12、13的点是端点,标号2、3、9、11的点是三叉点,标号8、14的点是四叉点。图4中甲骨文字形的顶点连接关系可以分为以下几类： 1) 端点与三叉点连接,如图4中顶点1与顶点2、顶点5与顶点4、顶点7与顶点6、顶点10与顶点9、顶点12与顶点11、顶点13与顶点14的关系即属于此类； 2) 端点与四叉点连接,图4中顶点13与顶点14的关系属于此类； 3) 三叉点与三叉点连接,如图4中顶点2与顶点3、顶点3与顶点4、顶点4与顶点6、顶点9与顶点11； 4) 三叉点与四叉点连接,图4中顶点2与顶点14、顶点3与顶点8、顶点6与顶点8、顶点9与顶点8、顶点11与顶点14的关系属于这一类； 5) 四叉点与四叉点连接,图4中顶点8与顶点14即属此类。对甲骨文字形的顶点进行进一步抽象,便得到甲骨文字形的拓扑图形,甲骨文字形“贞”的拓扑图形如图5所示。

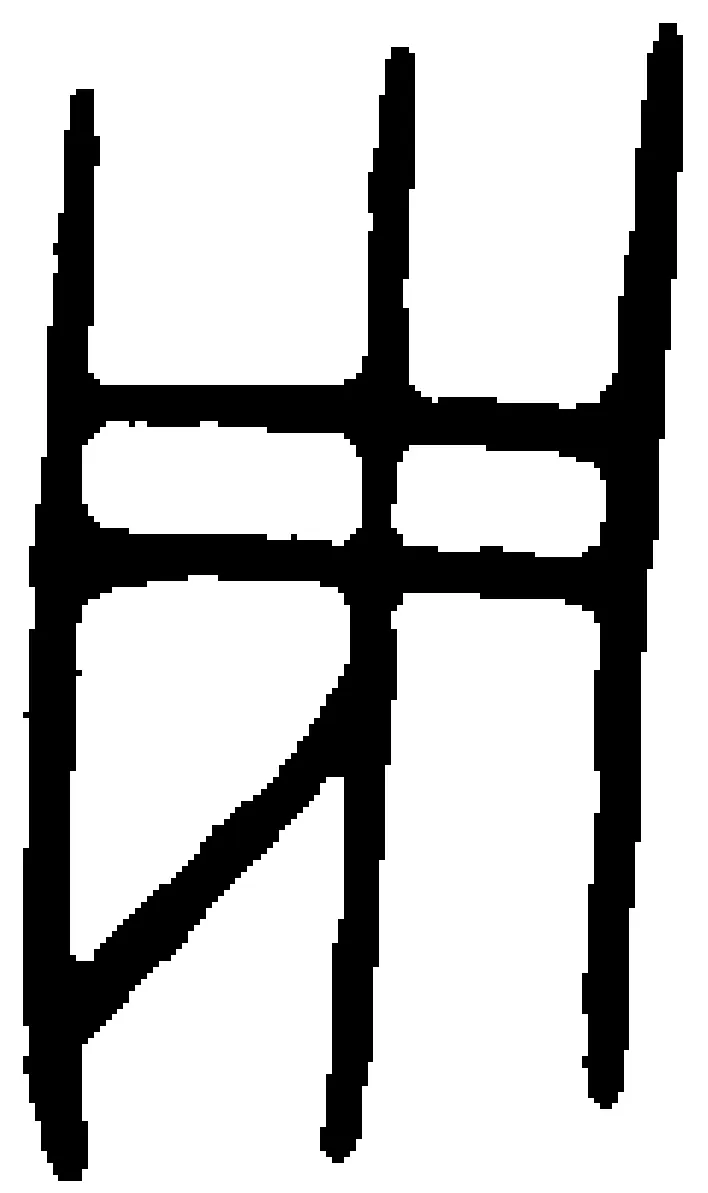
图2　甲骨文字形“贞”

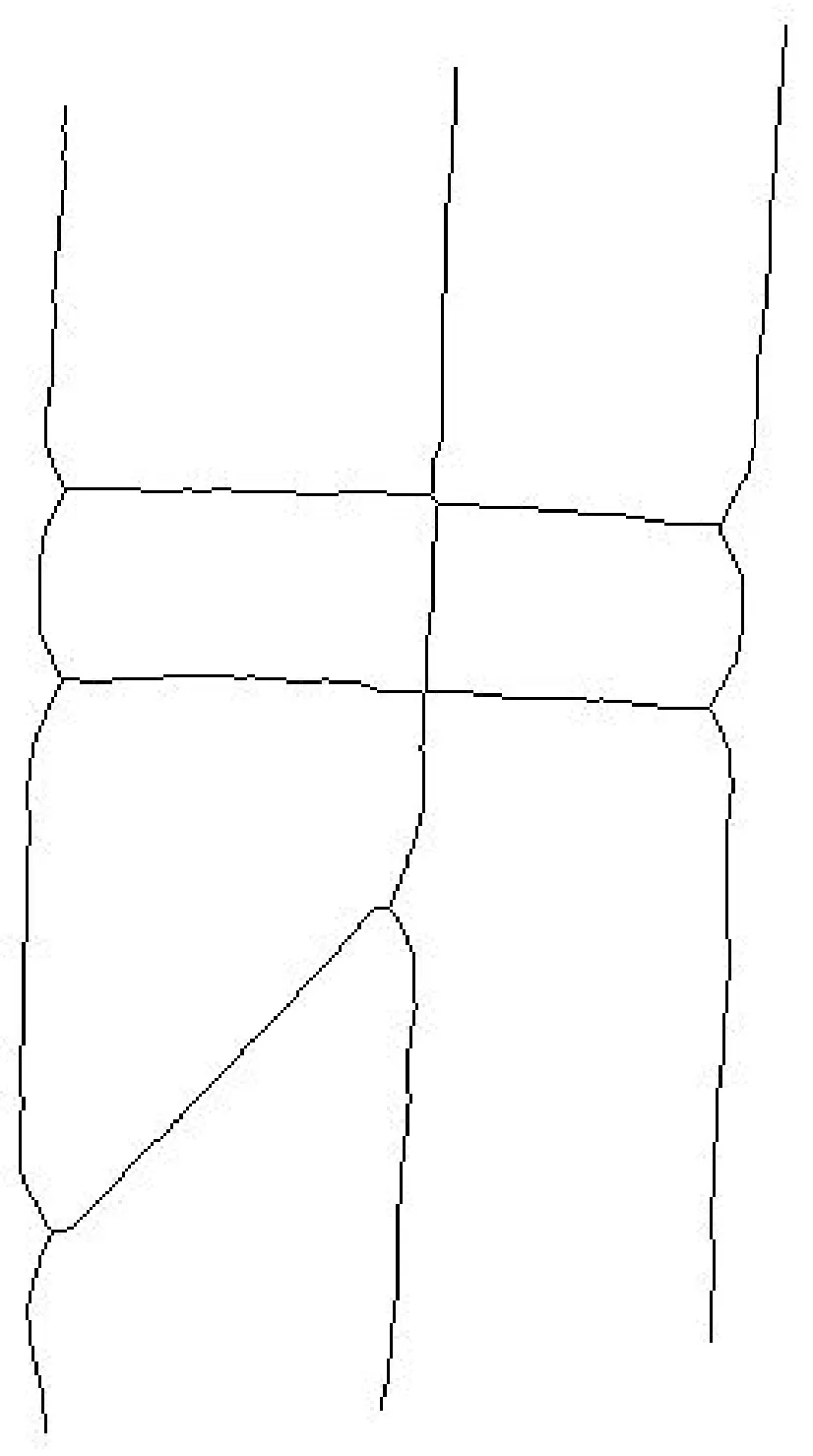
图3　细化后的字形

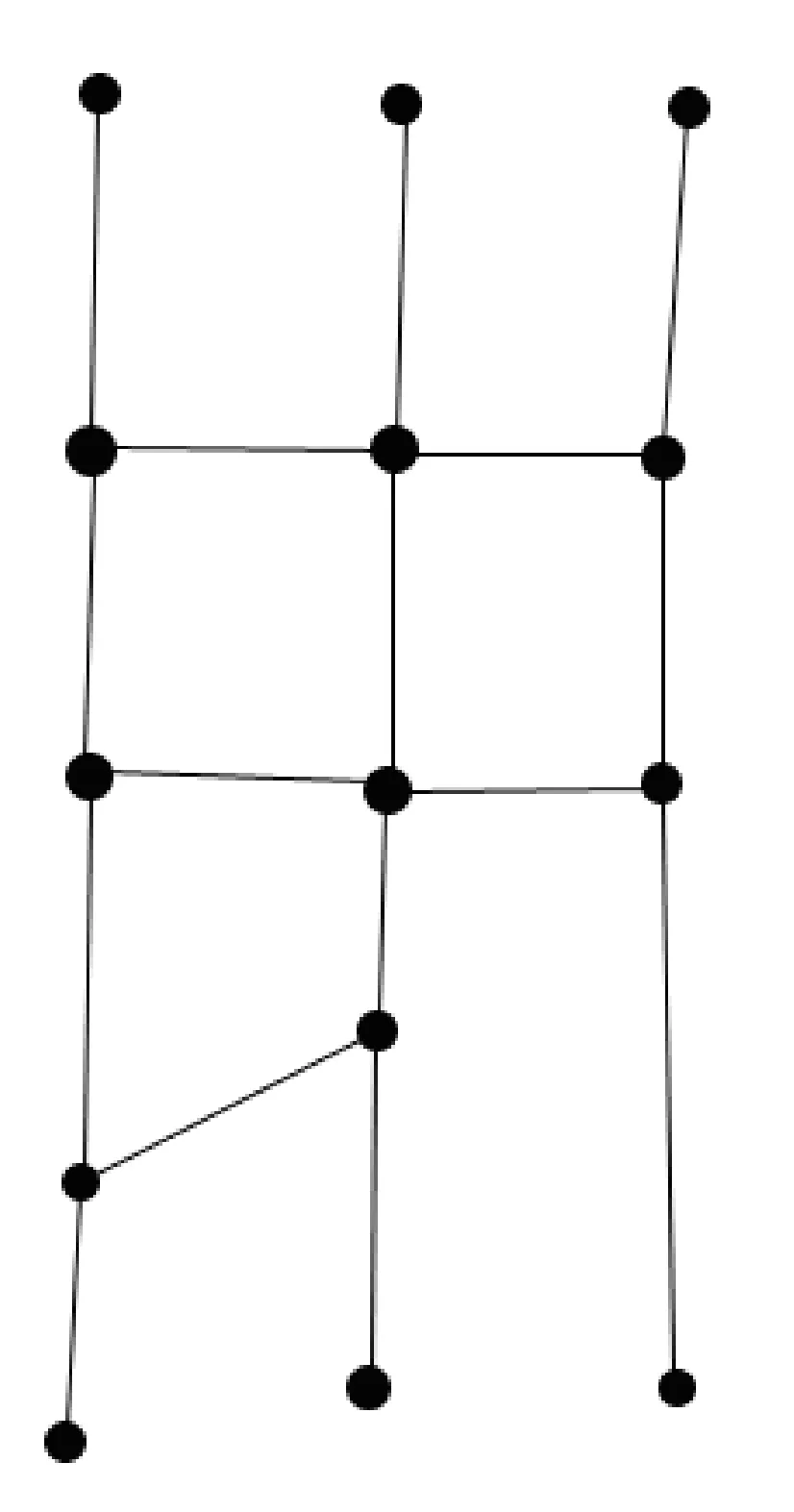
图4　细化字形“贞”的拓扑顶点

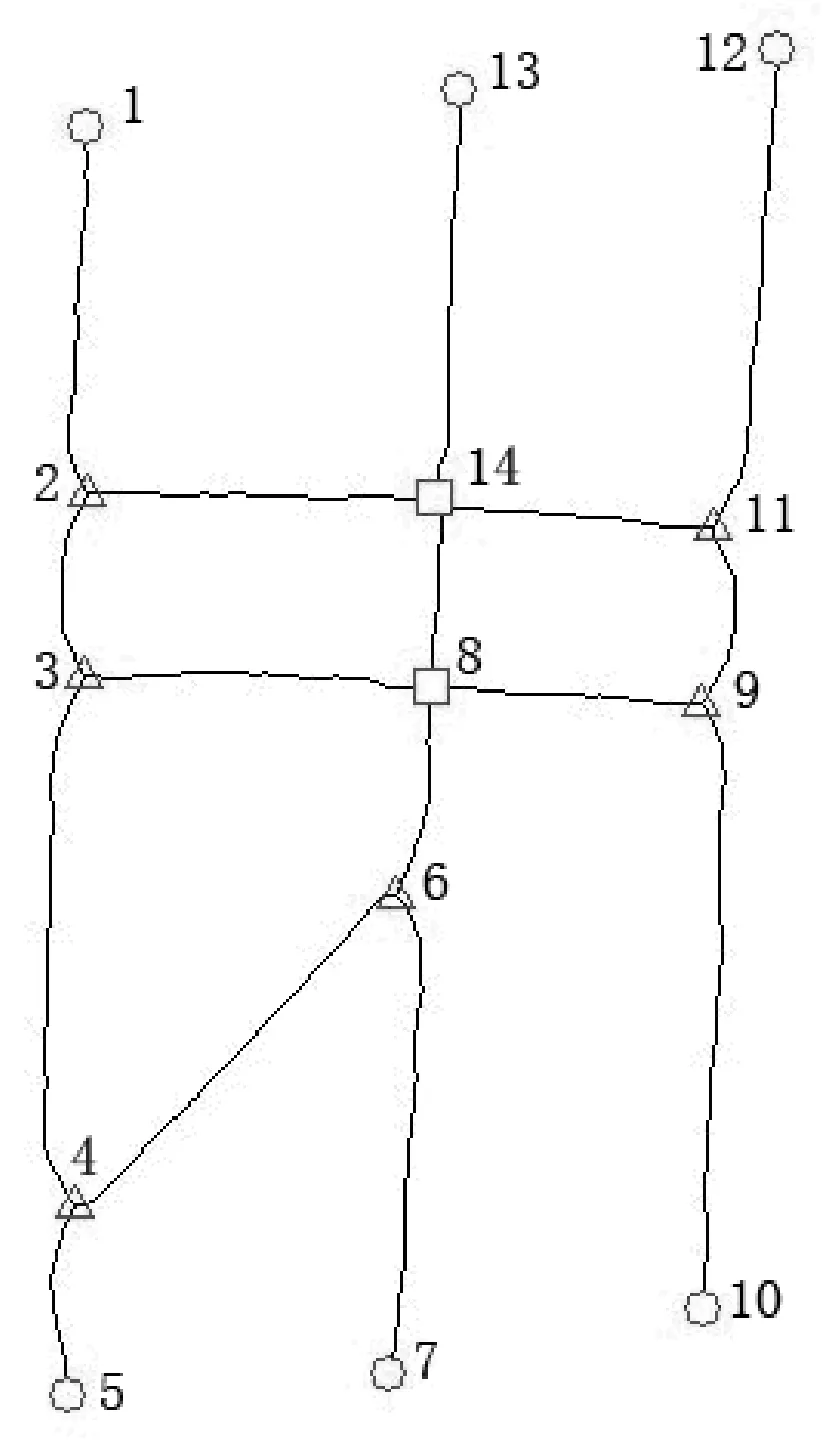
图5　“贞”的拓扑图形

提取字形图像的拓扑顶点的过程如下：先对字形图像进行细化处理,按照从上到下顺序扫描细化后字形图像的每一行的像素,对每一个像素应用八连通模板进行判断,如果像素在所有方向均无连通区域,则这一点为孤立点；如果像素只在一个方向存在连通区域,则这一点为端点；如果像素在三个方向存在连通区域,则为三叉点。四叉点、五叉点、六叉点依此类推。二叉点是指数为2的顶点,这类顶点在甲骨文字形中比较特殊。由于甲骨文书写材料的独特性以及甲骨文创制人员的复杂,使得甲骨文形态变化多样,一个甲骨文字形不同的人有多种不同的刻写方法,不同的契刻方法造就了不同的甲骨文形体。如果仔细观察这些不同形体的甲骨文字形就会发现,不同形体之间虽然笔画顺序以及组合关系不同,但是它们之间的大体结构却是相似的。从拓扑结构上来说,二叉点和弧线段、直线段不存在拓扑上的区别,但是有些二叉点却不宜与弧线段、直线段等同。因此,在具体处理中,需要对这两类二叉点区别对待。对于夹角大于90度的二叉点,可以将此二叉点关联的边视为弧线段或直线段。只需对夹角小于或等于90度的二叉点加以处理。由此可见,某些二叉点虽然可以显示字形刻写时形体上的差异,但并不一定能构成不同的甲骨文。对于字形的拓扑结构来说,也不会产生变化。

从以上对甲骨文字形顶点的分析可以看出,甲骨文字形拓扑顶点之间的拓扑关系可以表述为各顶点之间的连接关系。这种拓扑关系由甲骨文字形的各拓扑顶点以及拓扑顶点相互之间的连接关系唯一确定。因而甲骨文字形拓扑关系包括拓扑顶点的数目及拓扑顶点之间的连接关系。具有相同数目的拓扑顶点以及相同连接关系的拓扑空间之间可以建立一个同胚映射关系,因而是拓扑等价的。由此可见,拓扑顶点数量相同,拓扑顶点之间的连接关系不一定相同；拓扑顶点数量不同,拓扑顶点之间的连接关系必不相同；拓扑顶点之间的连接关系相同,拓扑顶点数量必相同；拓扑顶点之间的连接关系不同,拓扑顶点的数量未必不同。所以,如果两个字形的拓扑顶点数量相同,并且拓扑顶点之间的连接关系也相同的话,那么这两个字形一定是同一个字形。但是,甲骨文字形是一种字形结构不稳定的字形,同一个字有很多不同的写法,造成甲骨文中存在很多的异写字,拓扑顶点的数量、拓扑顶点之间的连接关系不同的字形却可能是同一个字,例如：与虽然拓扑结构不相同,但在甲骨文中却是同一个字“师”。

甲骨文字形的细化处理是提取甲骨文字形拓扑顶点的基础和先决条件,对于拓扑顶点的分析至关重要,没有甲骨文字形的细化处理便无法准确分析字形的拓扑顶点。目前,图像细化的处理算法有很多,大体上可以分为串行细化算法和并行细化算法。串行细化算法如Hilditch细化算法[9]、Pavlidis算法[10],并行细化算法如Rosenfeld细化算法[11],Zhang并行快速细化算法[12]等,Zhang并行快速细化算法细化之后的轮廓走势与原图保持得相对较好。因此,对于甲骨文字形的细化处理,本文采用Zhang并行快速细化算法。

2.3拓扑编码

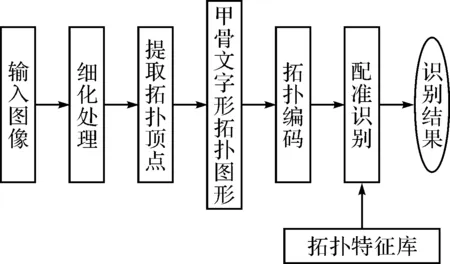
甲骨文字形的拓扑编码就是给甲骨文字形的每一种拓扑结构进行形式化的表达,通过这种形式化的表达,可以比较两个拓扑结构的异同。这种编码应该能够描述甲骨文字形的结构关系。在甲骨文字形拓扑顶点的各种连接关系中,端点与三叉点以及端点与四叉点的连接关系比较特殊。甲骨文中异体字繁多,存在正反无别的现象,由于甲骨文是由不同的书写者在不同的时期所作,因而对于同一字形书写方式各异,比如图6中a、b是同一个甲骨文字形“安”不同写法的细化图像。在图6a中端点与三叉点、四叉点的连接现象在图6b中消失了,但这并不妨碍我们把他们视为同一个甲骨文字形。因而甲骨文字形拓扑结构的编码应该具有这样的容错性和鲁棒性。由此可见,端点在甲骨文字形拓扑结构中并不是一个非常重要的因素。由定义可知,不同的叉点关联的边的数目不同,体现在拓扑结构上也必不相同,因此他们的权值也不相同。可以预见,W1

图6　甲骨文字形“安”的细化图像

令Nv、Ne、N0、N1、N2、N3、N4、N5、N6分别表示拓扑图形的顶点、边、孤立点(0叉点)、端点(1叉点)、二叉点、三叉点、四叉点、五叉点、六叉点的数目,N表示各叉点的权值之和,T表示甲骨文字形C的拓扑编码,R表示拓扑顶点之间的连接关系。那么一个甲骨文字形的拓扑结构的编码可以用一个4元组表示为

T(C)=(f1,f2,N,R)

其中,f1、f2分别为连通支、割点的数目,N=0×N0+0.1×N1+0.2×N2+0.3×N3+0.4×N4+0.5×N5+0.6×N6。R表示拓扑顶点之间的连接关系,可以用无向图描述如下：设G=(Nv,Ne)是具有Nv个顶点、Ne条边的图。G的邻接矩阵是具有如下性质的n阶方阵：

2.4甲骨文字形拓扑顶点关系的数据结构描述及

拓扑配准算法

从以上对甲骨文字形拓扑顶点关系的描述可以看出,决定甲骨文字形拓扑结构关系的要素有：连通支、顶点以及顶点之间的连接关系。顶点包括孤立点、端点、二叉点、三叉点、四叉点、五叉点和六叉点。根据甲骨文字形的拓扑结构关系,甲骨文字形拓扑图形的形式化描述可以通过建立拓扑顶点、连接矩阵等要素之间的数学关系来实现。

拓扑配准是将不同图形的拓扑结构进行匹配的过程,其一般步聚是：首先对两幅图像进行特征提取得到拓扑顶点；根据拓扑顶点之间的连续关系构造拓扑关系图；对拓扑关系图进行量化编码；通过进行相似性度量找到匹配的拓扑关系图。

拓扑配准可以定义如下：给定两幅待配准的图形的拓扑结构如下T1(x,y)和T2(x,y),称其中之一T1(x,y)为基准拓扑,另一个T2(x,y)为待配准拓扑,则称拓扑配准为两拓扑关系的映射变换。

T2(x,y)=g(T1(x,y))

这里,g为一个二维坐标变换。

特征提取和拓扑量化编码是拓扑配准的重要环节。特征提取是配准技术中的关键,准确的特征提取为特征匹配的成功进行提供了保障。因此,寻求具有良好不变性和准确性的特征提取方法,对于匹配精度至关重要。如果能够精确描述两幅不同字形图像的拓扑特征,就可以实现字形在拓扑关系上的配准。

综上所述,甲骨文字形拓扑图形的配准算法如下：

Step1:提取字形图形的拓扑顶点；

Step2:构造拓扑顶点之间的拓扑关系；

Step3:对字形的拓扑关系进行量化编码；

Step4:计算基准拓扑与待配准拓扑之间的距离；

Step5:小于给定阈值的两个拓扑间距离的字形图形被识别为拓扑等价,否则拓扑不等价。

甲骨文字形配准识别系统识别字形的流程如图7所示。

图7　甲骨文字形配准识别

在判定两个拓扑间是否等价的过程中,基准拓扑与待配准拓扑之间的距离的阈值的选取对于识别结果有着直接的影响。那么,阈值如何确定呢？一般来说,如果两个甲骨文字形的拓扑图形等价,即属于同一甲骨文,那么这两个拓扑图形之间的距离要小于不同甲骨文字的拓扑图形的距离。甲骨文中,同一甲骨文字的异写字形有很多,这些异写字形之间的拓扑距离要小于其与另一甲骨文字拓扑图形的距离。因此,确定阈值的一个合理的解决办法是,对每一个甲骨文字,计算此甲骨文字异写字形之间拓扑距离的值,在所有的甲骨文字中,找中两个异写字形的最大的拓扑距离,此距离作为阈值。

用数学语言描述如下：令T表示阈值,则

T=max{maxC1,maxC2,…,maxCn}

其中maxCn表示甲骨文字Cn的异写字形之间拓扑距离的最大值。

3　实验结果

我们在Windows环境下主频2.60GHz的计算机上,利用Visual C++ 6.0和OpenCV 1.0实现了上文提出的算法,设计了甲骨文字形自动识别系统。该系统的字库平台是自主开发的通用甲骨文 字库,该TTF格式字库建立在Windows环境下,字形采用基于二 次Bezier曲线的轮廓描述技术,字库含有甲骨文字形3673个。系统识别流程如下：对输入的图形进行细化处理后,由识别系统 提取细化后图形的顶点,构造甲骨文字形图形的拓扑图形,然后对拓扑图形进行数学描述。通过计算待配准拓扑与拓扑特征库中拓扑编码的距离,实现甲骨文字形的配准识别。识别的结果在计算机屏幕上用曲线轮廓甲骨文字形及对应的汉字显示出来,对于无法与现代汉字对应的字形直接显示曲线轮廓甲骨文字形。该识别系统对于甲骨文中的异写字具有一定的容错性和鲁棒性。实验结果表明,本文提出的算法,既可以识别目前已识读的甲骨文字形,也能够识别目前尚无法识读的甲骨文字形。

表1　实验数据表

4　结语

甲骨文作为我国最古老的成熟的系统文字体系,已经具备了较为稳定的拓扑结构特征,奠定了汉字形体拓扑结构的雏形。甲骨文字形异体字较多,但是同一字形的不同写法的拓扑特征具有稳定性,这也使得今天的人们能够从字形上区分不同的甲骨文字形。甲骨文字形的结构可以由构成甲骨文字形的拓扑顶点唯一确定。拓扑顶点之间不同的组合关系形成了不同的甲骨文字形。本文分析了甲骨文字形的拓扑结构,确定甲骨文字形的拓扑顶点,具体分析了甲骨文字形拓扑顶点之间的拓扑关系,通过对拓扑顶点、拓扑关系、拓扑编码相应的数据结构来刻画甲骨文字形顶点之间的关系,将图画性质的甲骨文字形转化为拓扑图形,并对每种拓扑图形进行编码,实现了对甲骨文字形的拓扑描述。在此基础上,利用拓扑配准的方法,通过计算基准拓扑与待配准拓扑之间的欧氏距离,实现基于拓扑结构的甲骨文字形的配准,从而识别甲骨文字形。

[1] 顾绍通,马小虎,杨亦鸣.基于字形拓扑结构的甲骨文输入编码研究[J].中文信息学报,2008,22(4):123-128.

GU Shaotong, MA Xiaohu, YANG Yiming.Topological Frame Based Input Method Coding of Jiaguwen[J].Journal of Chinese Information Processing,2008,22(4):123-128.

[2] 李继明.计算机文字信息处理技术新探——甲骨文象形码设计方案[J].中文信息学报,1996,10(3):18-29.

LI Jiming. A newly discovery on words processing technology——The design of pictographic code to inscriptions on bones or tortoise shells[J].Journal of Chinese Information Processing,1996,10(3):18-29.

[3] 肖明,赵慧,甘仲惟.甲骨文象形码编码方法研究[J].中文信息学报,2003,17(5):60-65.

XIAO Ming, ZHao Hui, GAN Zhongwei. Study for the method of Jiaguwen symbol coding[J]. Journal of Chinese Information Processing,2003,17(5):60- 65.

[4] 刘家锋,唐健华,黄降龙.基于HMM的联机汉字识别系统及其改进的训练方法[J].中文信息学报,2001,15(4):47-52.

LIU Jiafeng,TANG Jianhua,HUANG Xianglong. A HMM based on-line Chinese character recognition system and improved training algorithm[J].Journal of Chinese Information Processing,2001,15(4):47-52.

[5] 蔺志青,郭军.贝叶斯分类器在手写汉字识别中的应用[J].电子学报,2000,30(12)：1804-1807.

LIN Zhiqing,GUO Jun. An application of Bayesian classifier in the recognition of handwritten Chinese character[J].Acta Electronica Sinica, 2000,30(12):1804-1807.

[6] 周新伦,李锋,华星城,等.甲骨文计算机识别方法研究[J].复旦学报(自然科学版),1996,35(5)：481-486.

ZHOU Xinlun, LI Feng, HUA Xingcheng, et al. A method of Jia Gu Wen recognition based on a two-level classification[J].Journal of Fudan University(Normal Science),1996,35(5):481-486.

[7] 李锋,周新伦.甲骨文自动识别的图论方法[J].电子科学学刊,1996,18(增刊)：41-47.

LI Feng,ZHOU Xinlun. Recognition of Jia Wu Wen based on graph theory[J].Journal of Electronics,1996,18(supplied):41-47.

[8] 栗青生,杨玉星,王爱民.甲骨文识别的图同构方法[J].计算机工程与应用,2011,47(8)：112-114.

LI Qingsheng,YANG Yuxing,WANG Aimin.Recognition of inscriptions on bones or tortoise shells based on graph isomorphism[J].Computer Engineering and Application, 2011,47(8):112-114.

[9] Hilditch C J. Linear Skeletons from Square Cupboards[A].In:Meltzer,B. and Michie,D. eds,Machine Intelligence,New York:Elsevier,1969:403-420.

[10] Pavlidis T. A thinning algorithm for discrete binary images[J]. Computer Graphics and Image Processing,1980,13(2):142-157.

[11] Rosenfeld A. A characterization of parallel thinning algorithms[J]. Information Control,1975,29(3):286-291.

[12] Zhang T Y,Suen C Y. A fast parallel algorithm for thinning digital patterns[J]. Communications of the ACM,1984,27(3):236-239.

Identification of Oracle-bone Script Fonts Based on Topological Registration

GU Shaotong

(School of Linguistic Science and Art,Jiangsu Normal University, Xuzhou221009)

Oracle-bone script,as the character system with stable topological structure,although has many variant forms,same characters share the semblable topological structure for different forms. This characteristic makes it possible to identify different fonts based on the forms. By analyzing the topological characteristic,topological vertexes,and the topological relation among topological vertexes,the research describes the topological relation among topological vertexes and converts oracle-bone script fonts to topological graphs. Meanwhile,by coding the topological graphs,the authors realize the formal description of topological frame.

topological registration, topological frame, topological vertex, topological relation, topological coding, oracle-bone script, font identification

2016年4月10日,

2016年5月16日

国家社会科学基金(编号：13CYY039);教育部社会科学基金(编号：10YJC740032);江苏高校优势学科建设工程资助项目(编号：PAPD);江苏省高校哲学社会科学重点研究基地基金资助。

顾绍通，男，硕士，讲师，研究方向：中文信息处理。

TP391

10.3969/j.issn.1672-9722.2016.10.029