一种基于卡尔曼滤波的惯导系统综合校正算法*

秦立新

(海军驻上海江南造船(集团)有限责任公司军事代表室　上海　201913)



一种基于卡尔曼滤波的惯导系统综合校正算法*

秦立新

(海军驻上海江南造船(集团)有限责任公司军事代表室上海201913)

为了解除惯导系统在综合校正时必须处于水平阻尼条件下的限制,论文提出了一种基于卡尔曼滤波的无阻尼综合校正算法。首先,舰船在航行时处于无阻尼状态,并基于外测速度信息利用Kamlan滤波技术实时估测出系统的水平误差角；其次,将估测出的水平误差角引入到综合校正算法中进行解算,计算出陀螺漂移并进行补偿。通过仿真分析表明,系统在综合校正的过程中不再受到水平阻尼条件的限制,提高了惯导系统的长期定位精度。

惯性导航系统(INS); 综合校正; 卡尔曼滤波; 无阻尼

Class NumberTP301.6

1　引言

对于连续运行时间很长时间的船用惯性导航系统(INS),惯性指示位置和航向角的主要误差源是系统陀螺仪未被补偿的漂移误差。为了保持较高的位置精度和航向精度,需要对系统进行重调[1～2]。目前,很多学者对惯性导航系统综合校正技术进行了大量的研究工作,文献[3]介绍了基于OEPQ坐标系下综合校正算法,但此算法需要限制载体航行方式；文献[4]对平台式两点校进行了常值误差分析；但采用两点校等方法进行海上系统重调校正只是一种理想方式,系统水平阻尼工作状态要求舰艇在校正时必须处于匀速直航状态[5]。文献[6～7]虽然适用于捷联惯导系统且解除了舰船在等纬度航行的限制,但是也是在水平阻尼条件下进行综合校正。所以,近年出现的一些方案,在算法上存在局限性且忽略了舰船在机动状态下加速度对系统的干扰。

本文提出了一种新的综合校正方法,能在校正过程中解除对舰艇航行方式的限制:在校正过程中,使惯导系统处于无阻尼状态,基于外部速度观测信息,利用Kalman滤波估测出水平误差角,由于惯导处于无阻尼状态,不仅满足了舒拉振荡条件,并且提高了Kalman滤波器的可观测度[8～9],将Kalman滤波器估计出的水平误差角引入到传统综合校正过程中,建立综合校正方程,解算出导航系统的陀螺漂移和位置航向误差并补偿,完成惯导系统的综合校正[10～11]。最后对该综合校正方案进行仿真验证,并给出结论。

2　惯导系统水平误差角的估计

(1)

方程组(1)为动基座下无阻尼惯导系统误差方程。

式中,δL、δλ分别为纬度误差和经度误差；δVx、δVy分别为载体的东向速度误差和北向速度误差；ΔAx、ΔAy分别为东向和北向加速度计误差；fx、fy、fz分别为加速度计在x轴、y轴和z轴测量的比力信息；φx、φy、φz分别为载体x轴、y轴和z轴姿态误差角；εx、εy、εz分别为x轴、y轴和z轴陀螺漂移。

状态向量为

X=[δLδλδVxδVyφxφyφzεxεyεzΔAxΔAy]T

由式(1)和状态向量建立12维系统状态方程:

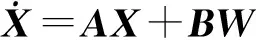
(2)

其中

W=[00axaywxwywz00000]T,

W为零均值的高斯白噪声。

其中系数矩阵A为

选取惯导系统解算速度和多普勒计程仪测量速度之差作为观测量,系统量测方程为

Z=HX+ν

(3)

式中,Z为系统的量测向量；H为系统的量测矩阵；量测噪声ν为零均值高斯白噪声。

量测量为

其中,Vs为地理坐标系下惯导系统解算的速度信息；Vsx,Vsy为Vs在地理系水平方向上的分量；Vd为地理坐标系下多普勒计程仪输出的载体艏艉向速度信息,其中

K为航向角。

量测矩阵为

把方程(2)和(3)离散化,得

(4)

最后,由式(4)采用Kalman滤波估计惯导系统水平误差角。

3　无阻尼综合校正方案设计

为了解除综合校正对载体航行姿态的限制,同时减小引入的新的动态误差,设计的方案中将式(4)估计出的惯导系统水平误差角φx、φy带入到校正算法中进行解算,同时在校正时间段内,系统工作于无阻尼状态。

惯导平台坐标系相对地理坐标系误差角为

(5)

式中,θx、θy、θz为计算机坐标系与地理坐标系的夹角；ψx、ψy、ψz为平台坐标系相对计算机坐标系的误差角。

引入Kalman滤波估计的结果,由于方位误差角φz估计效果不理想,因此方位信息仍由外界信息获得。对式(5)做变换:

(6)

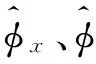
由图1可知,方位误差角φz=δK,根据校正原理得到:

(7)

令

图1　φz与δK的关系

因此,P(tN)=M(tN)ψ(tN),再由平台漂移角ψ和陀螺漂移ε之间的关系可得

ΩU-1(tN,tN-1)M-1(tN)P(tN)

(8)

式中,

Ω为地球自转角速度。

结合式(5)～式(8),即可估算出陀螺漂移并实现无阻尼条件下的综合校正。

本方案整体流程图如图2所示。

通过综合校正整体流程图可以看出,首先利用外部观测信息和卡尔曼滤波器估出水平误差角,重调开始时利用外部提供的精确经纬度信息和航向信息对系统进行重调,并利用估测出的水平误差角建立位置误差和陀螺漂移的关系,在第二点取得信息后利用估测出的水平误差角和外部观测信息计算出陀螺漂移并进行补偿。同时又对系统进行重调。

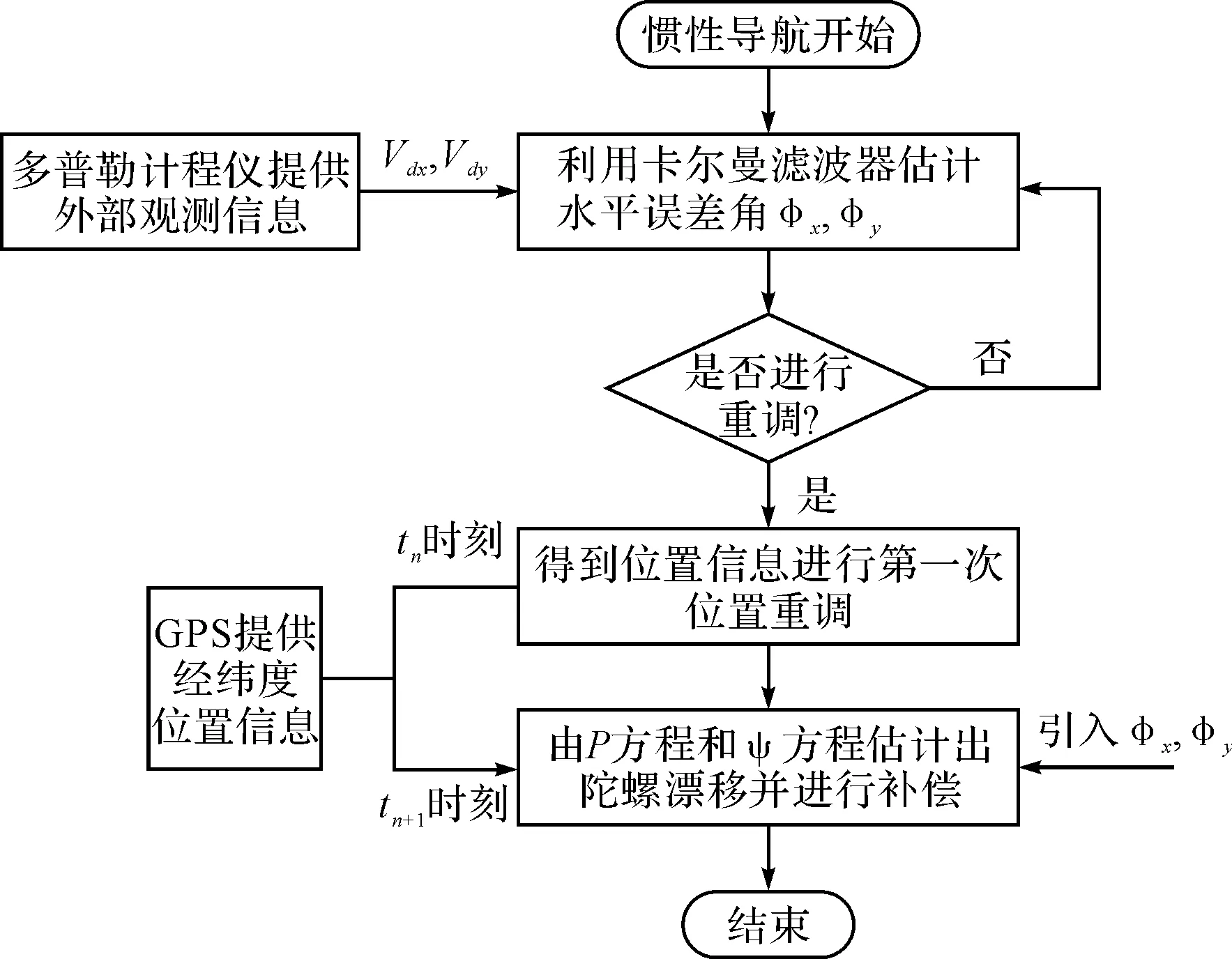
图2　综合校正整体流程图

4　仿真研究

仿真结果如图3～图5所示。

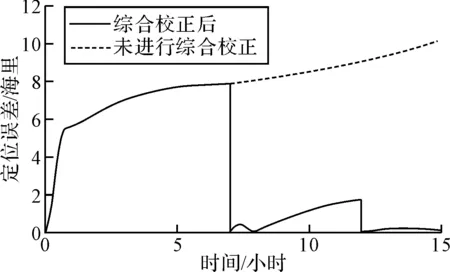
图3　定位误差

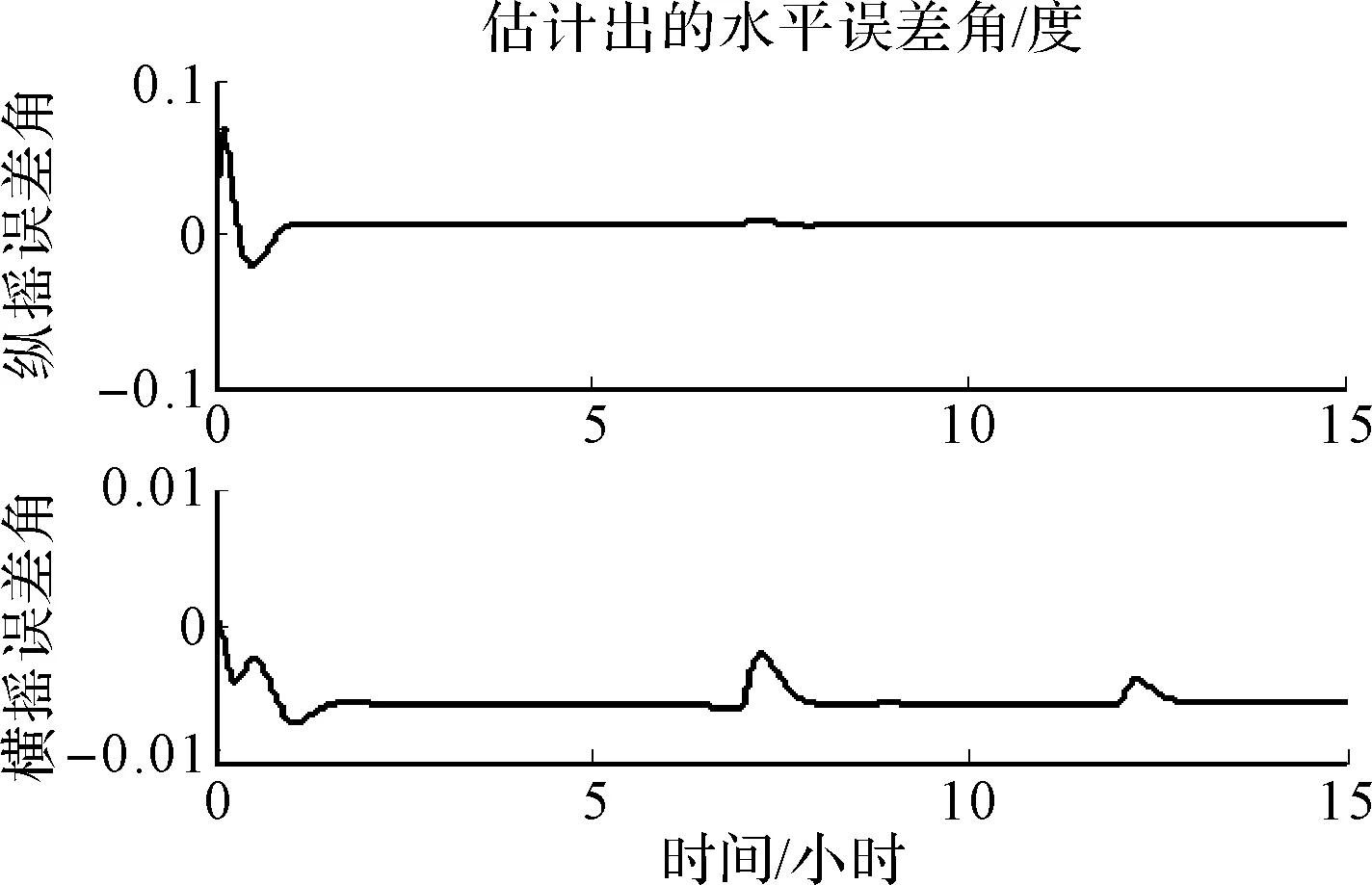
图4　估计出的水平误差角

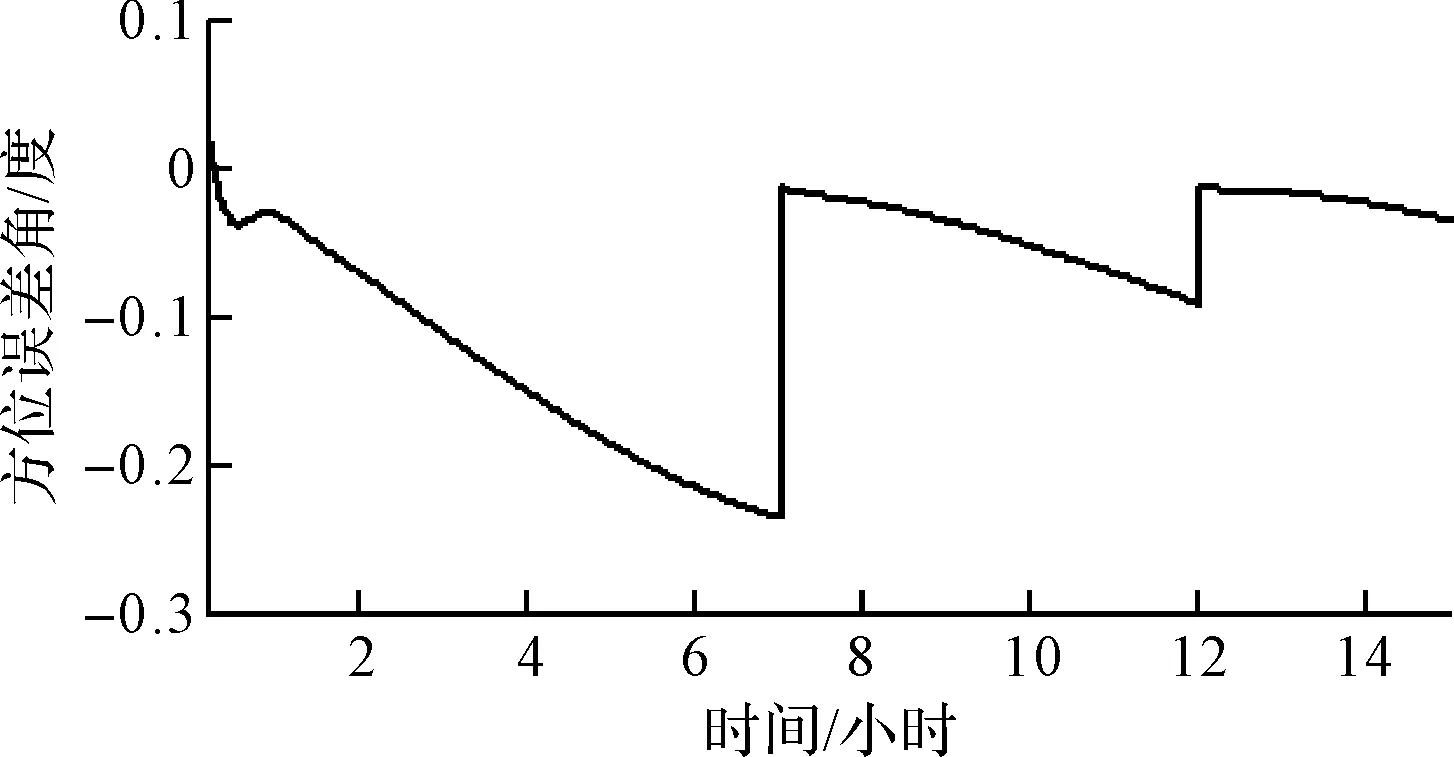
图5　方位误差角

舰船航行7小时的时候利用外部参考信息进行第一次系统重调并将估测出的水平误差角带入综合校正算法中进行第一点解算,5小时后再利用外部位置信息进行海上重调,此时将7～5小时期间估测出的水平误差角引综合校正算法中进行解算,估测出陀螺漂移并进行补偿。方位误差角的估计如图5所示。由图3～图5可以看出在第12小时综合校正后舰船的速度及经纬度都得到了很好的校正且定位误差和方位误差允许范围内,说明此方法的可行性。

5　结语

本文提出的综合校正方法,在校正过程中解除对舰艇航行时必须处于水平阻尼条件下的限制,基于外部速度观测信息,利用Kalman滤波估测出水平误差角,将其引入到传统综合校正过程中,在惯性坐标系下建立综合校正方程,由传统校正算法解算得到导航系统的陀螺漂移和位置航向误差并补偿,完成惯导系统的综合校正。

[1] 高钟毓.惯性导航系统技术[M].北京:清华大学出版社,2012:143-144.GAO Zhongmin. Inertial navigation systems technology[M]. Beijing: Tsinghua University Press,2012:143-144.

[2] Donald R. Watland, Peoria, Ariz. Orthogoanl Polar Coordinate System to Accommodate polar navigation[P]. United States Patent,1995.

[3] 黄德鸣,程禄.惯性导航系统[M].北京:国防工业出版社,1986:66-90.

HUANG Deming, CHENG Lu. Inertial Navigation System[M]. Beijing: National Defense Industry Press,1986:66-90.

[4] 杨晓东,邓太光.平台式惯导系统两点校的常值误差分析[J].交通运输工程学报,2011,11(3):100-104.

YANG Xiaodong, DENG Taiguang. Constant error Analysis of two-point calibration on Platform Inertial Navigation System[J]. Journal of Traffic and Transportation Engineering,2011,11(3):100-104.

[5] 邓太光,杨晓东.一种平台式惯导系统两点校方法的改进[J].控制工程,2011,18(SI):23-36.DENG Taiguang, YANG Xiaodong. A better two-point calibration method for Platform Inertial Navigation System[J]. Control Engineering,2011,18(SI):23-36.

[6] 高伟,史洪洋,张鑫,等.基于位置信息的捷联惯导系统综合校正技术[J].华中科技大学学报(自然科学版),2014,42(6):101-106.

GAO Wei, SHI Hongyang, ZHANG Xin, et al. Iintegrated correction based on position information SINS[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition),2014,42(6):101-106.

[7] 张鑫.船用单轴旋转光纤陀螺捷联惯导初始对准/测漂及综合校正研究[D].哈尔滨:哈尔滨工程大学,2012:103-105.

ZHANG Xin. Research on Initial Alignment/evaluation of the Inertial Sensor Error and Comprehensive Correction for Shipboard Single-axial Rotary Fiber-Gyroscope Inertial Navigation System[D]. Harbin: Harbin Engineering University,2012:103-105.

[8] 秦永元,张洪钺,汪淑华.卡尔曼滤波与组合导航原理[M].西安:西北工业大学出版社,1998:48-55.QIN Yongyuan, ZHANG Hongyue, WANG Shuhua. Kalman filtering and navigation principle[M]. Xi’an: Northwestern Polytechnical University Press,1998:48-55.

[9] 付梦印,邓志红,闫莉萍.Kalman滤波理论及其在导航系统中的应用[M].北京:科学出版社,2010:92-100.

FU Mengyin, DENG Zhihong, YAN Liping. Kalman filtering theory and its application in navigation system[M]. Beijing: Science Press,2010:92-100.

[10] 吴俊伟,曾启明,聂莉娟.惯性导航系统的误差估计[J].中国惯性技术学报,2002,10(6):1-5.

WU Junwei, ZENG Qiming, NIE Lijuan. Estimation of INS’s error[J]. Journal of Chinese Inertial Technology,2002,10(6):1-5.

[11] 徐景硕.固定点平滑技术在惯导对准精度评估中的应用[J].测控技术,2004,23(11):74-76.

XU Jingsuo. Application of fixed point smoothing to the testing and evaluation of INS in-flight alignment[J]. Measurement & Control Technology,2004,23(11):74-76.

A Comprehensive Calibration Algorithm Based on Kalman fliter for Inertial Navigation System

QIN Lixin

(Naval Representative Office in Shanghai Jiangnan Shipyard(Group) Co., Ltd, Shanghai201913)

In order to lift the restrictions that the inertial system in comprehensive correction must be in a horizontal damping condition,this paper proposes an undamped comprehensive correction algthm based on Kalman filter. Firstly,the ship is sailing with the undamped state, and the Kalman fliter is used to real time estimate horizontal-angle error based on the velocity observations. Secondly horizontal error of estimated angle is taken into the comprehensive correction algorithm for solving, then the gyro drift is calculated and compensated. The simulation results show that the system is no longer subject to the horizontal damping conditions in the process of comprehensive correction and increase the long-term positioning accuracy of inertial navigation system is increased.

inertial navigation system(INS), comprehensive calibration, Kalman filter, undamped

2016年4月13日,

2016年5月20日

秦立新,男,工程师,研究方向:舰船电气。

TP301.6

10.3969/j.issn.1672-9722.2016.10.010