数值流形程序开发设计及其应用

焦　健

(北京城建设计发展集团股份有限公司，北京　100037)



数值流形程序开发设计及其应用

焦健

(北京城建设计发展集团股份有限公司，北京100037)

针对数值流形程序开发面临覆盖系统剖分算法、基于覆盖的平衡方程的建立、接触问题处理等几个难题，提出了具体的解决对策，完成了数值流形程序的编制，并通过算例验证了该程序的可靠性，展现了该程序在处理不连续变形计算方面的独特优势。

数值流形方法，不连续变形计算，程序开发

数值流形方法(NMM)诞生于岩石力学领域，是由石根华博士在创立非连续变形分析[1](DDA)之后提出的一种新型的数值计算方法。它通过采用连续和非连续覆盖函数的办法，将有限元与DDA整合到一种计算模式下[2]。

自数值流形方法提出以来一直颇受关注与好评，但石根华博士的数值流形程序并未在国内作大力推广，而科研工作者独自将其编程实现又面临诸多困难[3,4]，因此数值流形方法在国内的研究和应用还仅限于为数不多几个科研机构。在前人工作的基础上[5]，完成了数值流形程序的开发设计，并成功地用于几个实际问题的解决，取得了满意的结果。本文重点介绍数值流形程序编制中几个难点问题的解决方法。

1　覆盖系统自动剖分算法

数值流形方法中采用两套独立的网格，物理网格和数学网格。物理网格为材料固有边界和内部裂纹；数学网格可以由常规的网格，如有限元网格、规则的格子或级数收敛域转化而得到。采用三角形或四边形有限元网格，可以方便地取节点的形函数作为覆盖函数的权函数，是目前主要的数学网格形式。二者相比，四边形有限元网格具有拓扑运算简单、同阶覆盖函数条件下精度更高的优势。此外，数值流形方法并不要求数学网格与求解域完全吻合，而是能够覆盖整个求解域即可。所以，即使在边界不规则处也无需调整网格形状以适应边界条件。基于上述考虑，本文采用矩形数学网格，在此基础上完成划分流形单元和覆盖系统自动剖分的工作。

如图1所示，粗线为材料物理网格，细线为数学网格(图中一个基本数学网格定义为一个数学单元，如数学单元1-2-5-4)。基于数学网格节点定义了数学覆盖：包含某节点的所有数学单元的并集称为一个数学覆盖，如节点5所对应的数学覆盖为矩形区域1-3-9-7。一个数学覆盖可以被物理网格剖分为若干物理覆盖，如数学覆盖1-3-9-7被物理网格剖分出六个独立的子区域，其中只有13-15-16-26-22和22-26-19-20两个子区域位于材料内部，成为两个物理覆盖。流形单元是数值流形方法的最小积分单位，它是若干个物理覆盖的交集。在矩形数学网格的条件下，流形单元必定是四个物理覆盖的交集。流形单元上的位移函数是这四个物理覆盖上的覆盖函数加权之和。编制数值流形程序的第一个困难就是在两套网格的叠加下搜索记录所有流形单元，以及每个流形单元所属的物理覆盖。

本文采用的覆盖剖分算法如下：循环每一条物理网格与数学网格线做求交运算，交点将每条物理网格划分为若干段，记录每一段物理网格。同时，数学单元在物理网格的剖分下出现若干个子区域。若子区域位于材料内部，则构成一个流形单元，并为流形单元添加一个成员变量，记录其所在的数学单元的四个节点；位于材料外部则不予考虑。如图1中数学单元1-2-5-4被剖分成23-5-24-22，21-22-24和1-2-23-21-4三个子区域，只有前两个子区域位于材料内部，属于流形单元，最后一个子区域无需处理。整个系统完成全部流形单元的搜索后如图2所示。

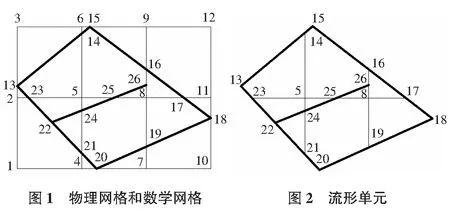
再对每一个数学网格节点进行循环，获得各个节点所对应的物理覆盖。算法如下：针对当前数学网格节点，搜索所有包含当前节点的流形单元并求其并集，构成该节点的数学覆盖。然后，令物理网格对该数学覆盖进行剖面，剖分处的每一个单独区域即构成一个物理覆盖，将其编号记录。

获得物理覆盖之后，便可以搜索每个流形单元所属的物理覆盖。如前述，每一个流形单元均记录了其所在数学单元的四个节点，这四个节点均对应若干个物理覆盖，依次对该流形单元与四个节点的物理覆盖进行分析，判断流形单元完全包含于哪个物理覆盖中，共可以找到四个物理覆盖，这四个物理覆盖即为该流形单元所属的物理覆盖。

2　覆盖函数和权函数

取覆盖函数为常函数，矩形有限元的形函数作为权函数，即：

(1)

(2)

其中，ui，vi分别为x向，y向的覆盖函数；We(i)为流形单元第i(i=1～4)个物理覆盖的权函数，采用的是流形单元所在矩形数学单元的形函数[9]。

则流形单元上的总体位移函数可表示为:

(3)

其中，

Te=[Te(1)(x,y),Te(2)(x,y),Te(3)(x,y),Te(4)(x,y)]

(4)

(5)

De={De(1),De(2),De(3),De(4)}T

(6)

其中，De(i)为流形单元第i(i=1～4)个物理覆盖上的常覆盖函数{ui,vi}。

3　平衡方程的建立

数值流形方法依据最小势能原理建立平衡方程。总势能包括：应变势能、初应力势能、荷载势能、惯性力势能、弹簧势能和接触摩擦力势能。对它们分项求导使势能极小化则可得总体平衡方程:

(7)

其中,总刚度矩阵K由单元刚度矩阵、固定点矩阵、惯性力矩阵和接触弹簧矩阵迭加得到，各矩阵的具体形式及计算某些矩阵元素涉及到的单纯形积分问题见文献[2]。荷载矩阵由F初应力矩阵、点荷载矩阵、分布荷载矩阵、体荷载矩阵、速度矩阵以及接触摩擦力矩阵迭加组成。文献[2]给出了除分布荷载矩阵外其他矩阵的具体形式；而在实际问题中，分布荷载也是很常见的荷载形式。本文推导建立了分布荷载矩阵。

作用于某条边上的分布荷载通常会跨越多个流形单元，首先搜索获得荷载通过的所有流形单元，再逐个为这些单元添加分布荷载矩阵。以图3中单元A-B-C为例推导分布荷载矩阵。

设A点(x1,y1)和B点(x2,y2)处的荷载集度分别为(fx1,fy1)，(fx2,fy2)。AB边上任一点的坐标和荷载集度可表示为:

(8)

(9)

继而，分布荷载在该单元上的势能有如下表达式:

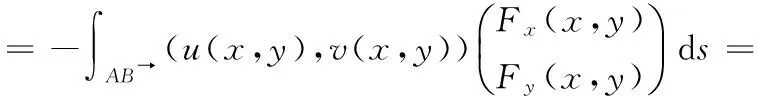
(10)

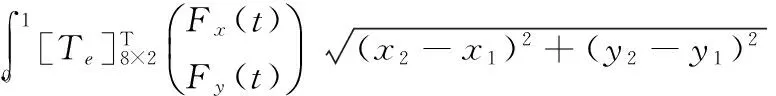
4　接触问题的处理

为了保证不连续边界在变形过程中满足两接触边之间无拉力、无嵌入，数值流形方法在接触位置设置数值上的“法向接触弹簧”；同时，为了模拟不连续面的抗剪能力，还在接触位置处设置了“切向接触弹簧”。

在本文的程序中，设定所有接触的初始状态都是锁定的，即法向弹簧和切向弹簧同时对接触两侧的相对位移起着限制作用。施加荷载后，随着变形的继续发展，接触可以在锁定、滑动和张开三种模式之间转换(称为开合迭代)，以模拟不连续面闭合、滑动和张开三种不同的状态。接触三种模式间的转换对平衡方程的影响见文献[2]。

接触位置的确定，文献[6]给出如下原则：

接触面的边缘是：1)块体的边界；2)材料场中裂缝两侧的一边。

接触的顶角可以是：1)物理边界或裂缝的顶端；2)块体边界或裂缝的三角形的交点。

在各种接触情形中，接触面的边缘一定如上所述是块体的边界或裂缝的一边；而接触的顶角却不仅限于上述两种情况。如图4所示，双层简支梁中部受集中荷载作用。如果只在裂缝的顶端，即A，B两点设置接触弹簧，虽能确保裂缝顶端处不发生嵌入，却不能避免在不连续面的其他部位发生嵌入。计算后的变形如图5所示。

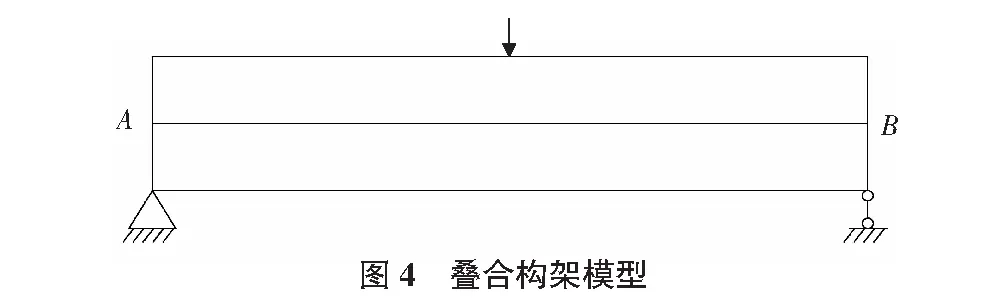
故本文除了在裂缝顶端及裂缝交点处设置初始接触之外，还在裂缝的整个长度范围内的每个单元顶点处设置了“初始假接触”。与裂缝顶端处的初始接触不同，这些接触的初始状态不是闭合而是张开的，即并没有设置法向和切向弹簧。只有在计算过程中当这些接触位置发生嵌入时，才添加接触弹簧，令其从张开变为锁定。之后，这些接触也可以随着变形的发展，在锁定、滑动和张开三种模式下进行转换。图6为上述双层简支梁采用“初始假接触”的办法计算后的变形图。可见，这种处理方式可以有效地避免在不连续面任意位置发生嵌入。

5　应用算例

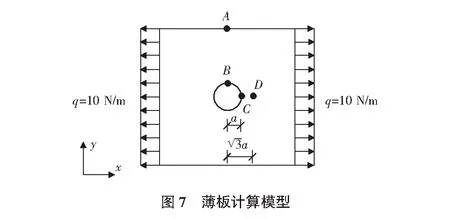
用有解析解的连续体变形问题验证了本文程序计算结果的可靠性，薄板计算模型见图7，表1给出一带圆孔薄板的应力结果比较。

表1　计算结果对比

程序在模拟不连续变形方面也取得了满意的结果。图8，图9为双层构架受集中力的变形情况。

6　结论及展望

采用本文所述主体思路完成的数值流形程序能够用于材料变形分析，经验证，计算出的变形及应力场符合理论解。特别是接

触弹簧及开合迭代算法的应用，使程序在进行不连续变形分析方面具有独特的优势。目前，数值流形程序中材料的本构方程仍然是基于弹性理论的线性方程，下一步的工作将研究改进现有的弹性本构，以期描述岩土材料的非线性永久变形和应变软化特征。

[1]Shi Genhua. Block system modeling by discontinuous deformation analysis [M].Southampton:Computational Mechanics Publications,1993.

[2]Shi Genhua.Numerical Manifold Method.In:Proc of IFDDA’96.Berkeley,California,USA:Tsi press,1996:52-204.

[3]Chen G，Miki S，Ohnishi Y.Automatic Creation of Mathematical Meshes in manifold method of Material Analysis [A].In:Working Forum on the Manifold Method of Material Analysis[C].California， USA:[s n.]，1995:105-126.

[4]曹文贵，速宝玉.流形元覆盖系统自动形成方法之研究[J].岩土工程学报，2001，23(20):187-190.

[5]蔡永昌，朱合华，夏才初.流形方法覆盖系统自动生成算法[J].同济大学学报，2004，32(5):585-590.

[6]石根华.数值流形方法与非连续变形分析[M].裴觉民，译.北京：清华大学出版社，1997.

Numerical manifold program development design and application

Jiao Jian

(BeijingUrbanConstructionDesign&DevelopmentGroupCo.,Limited,Beijing100037,China)

In light of cover system subdivision algorithm of numerical manifold program, based on over balancing equation establishment and contact problems processing and other difficulties, the paper puts forward specific solving countermeasures, finishes numerical manifold program compilation, testifies the program reliability through checking, and finally shows its unique advantages in processing discontinuous deformation computation problems.

numerical manifold method, discontinuous deformation computation, program development

1009-6825(2016)08-0256-03

2016-01-05

焦健(1981- )，男，工程师

TB115

A