考虑水平应力分布的深地下圆形洞室弹性解

尤业超　韩　阳　卞少帅

(解放军理工大学国防工程学院，江苏 南京　210007)



考虑水平应力分布的深地下圆形洞室弹性解

尤业超韩阳卞少帅

(解放军理工大学国防工程学院，江苏 南京210007)

在地层结构法的基础上，考虑水平应力在纵向线性分布，利用弹性力学计算方法得出深地下圆形洞室结构的弹性解，计算结果更接近于深地下工程的岩体水平应力线性分布实际情况。

圆形洞室，应力函数，水平应力，弹性解

0　引言

在利用地层结构法[1]进行深地下圆形洞室弹性计算时，往往有如下基本假设：

1)地层岩体和初砌支护材料为线弹性体；

2)圆形洞室为深埋洞室，不考虑地表边界产生的影响；

3)地层为无限大弹性平面；

4)地层初始应力作用在无限远处。假定埋深后，地层初始应力的垂直应力为σv=p，水平应力为σH=λp(λ为常数)，故而地层的垂直应力和水平应力均为常数。该种计算方法认为洞室为深埋洞室，水平应力的垂直分布对结构计算影响较小，基本可以忽略。然而，深地下应力状态非常复杂，除了地层自重应力外，还存在构造应力。因此，对于复杂地应力下的大断面地下圆形地下结构工程，水平应力的纵向分布应给予考虑。本文假定水平应力呈线性分布，求解深埋圆形洞室结构线弹性应力解。

1　基本参数假设

本文基于地层结构法基本假设外，还考虑呈线性分布的水平应力。设一点在地下埋深h处，以此处作为原点，距原点距离为r处，其纵向应力由构造应力和覆盖层岩体材料的自重(设重度为γ，岩体水平压力分布系数为K)。设垂直应力σv=q0，水平向考虑构造应力和岩体材料的侧压力的分布，设σh=q1+Ky，用极坐标形式为σh=q1+KRsinθ。

计算模型如图1所示。

2　深地下圆形洞室弹性计算

2.1应力函数设定与求解

在r处任意一点的初始应力转换成极坐标表示形式，其计算公式如下：

(1)

其中，σv为垂直应力；σh为水平应力；σr为径向应力；σθ为环向应力；τrθ为剪应力。

将σv和σh代入式(1)，整理可得初次应力:

(2)

故而假设二次应力状态下的应力函数为:

Φ=f1(r)+f2(r)sinθ+f3(r)cos2θ+f4(r)sin3θ

(3)

将该应力函数代入相容方程[2]中可得下式：

(4)

由于sinθ，cos2θ，sin3θ非线性相关，故可得式(5)。

(5)

利用欧拉公式求解得：

(6)

2.2二次应力场

根据弹性力学中极坐标下应力与应力函数计算公式[3]解各个应力关系式：

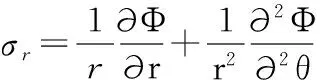
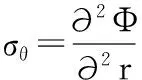
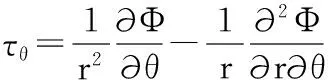
计算模型的边界条件主要从以下几个方面考虑：1)由释放荷载引起的附加应力场应力分量σr2，σθ2在无限远处的值为0；2)由释放荷载所引起的附加应力场应力分量在r=R处等于释放荷载的大小，即：σr2|r=R=ΔσrR,τrθ2|r=R=ΔτrθR；3)考虑径向和环向位移周期性变化规律和对称性变化规律。从而可得出相应的 f1(r)，f2(r)，f3(r)，f4(r)中各个参量的值(假设圆形洞室半径为R)，计算结果如表1所示。围岩二次应力场中的各点应力分量是由围岩的初始应力场与由释放荷载引起的附加应力场叠加而成的[1]。故而二次应力场的应力分量计算如表1所示。

表1　应力函数中各参量数值

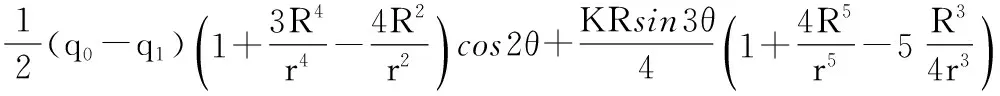
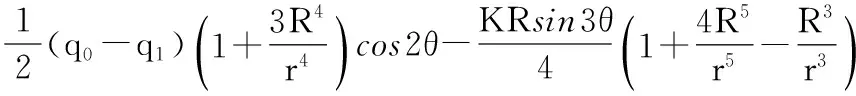
当K=0时，即不考虑水平应力的分布，各应力分量等于地层结构法中二次应力场的各应力分量。

2.3初砌内力和三次应力场计算

围岩的三次应力场是由初砌与围岩的接触应力引起的附加应力与二次应力场叠加产生的。设圆形衬砌在围岩的接触面上的任意点R的接触应力为:σrR=s0+s1sinθ+s2cos2θ+s3sin3θ。τrθR=0。其中，s0，s1，s2，s3均为常数。

按照地层结构法中的初砌内力和三次应力场计算方法可求得初砌内力和三次应力场的应力解。本文限于篇幅不再推导。

3　算例

假设现有一个圆形地下洞室埋深500m，洞室直径10m。地层平均岩层重度为25kN/m3，水平应力取垂直应力的0.7倍。分别利用地层结构法和本文计算公式计算洞顶和洞底以外1m处的径向应力值。分析水平应力分布的影响。计算结果见图2，图3。

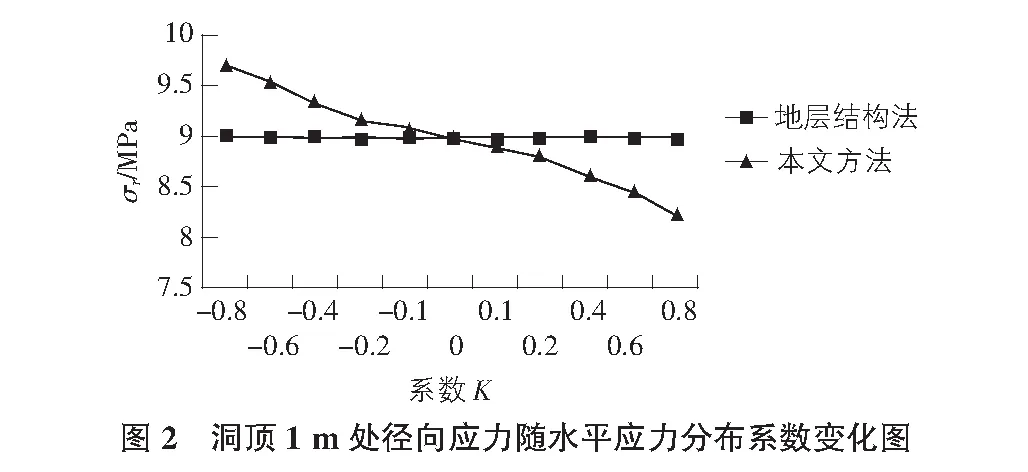
图2和图3表明：当K值较小时，文中的计算结果接近于地层结构法的计算结果，而当K值较大时，本文计算方法计算的径向应力值偏离地层结构法的计算结果。

4　结语

在地层结构法基础上考虑水平应力垂直方向的线性分布情况并进行理论推导，得出如下结果：

1)设定新应力函数，利用现有的边界条件推导出圆形洞室结构(未支护情况下)线弹性应力解(二次应力场，即未支护情况下的应力状态)，并为三次应力状态下的线弹性应力解推导提供思路；2)水平应力的线性分布转化为三角函数形式的思路为考虑水平应力复杂分布的应力分量求解提供借鉴作用。

[1]刘新宇.地下结构计算理论[M].南京：解放军理工大学工程兵工程学院，2012:33-41.

[2]徐秉业,刘信声.应用弹塑性力学[M].北京：清华大学出版社,1995:150-163.

[3]徐芝纶.弹性力学简明教程[M].北京：高等教育出版社,2013:75-79.

Elastic solution of deep underground circular cavity with horizontal stress distribution

You YechaoHan YangBian Shaoshuai

(CollegeofDefenceEngineering,PLAUniv.ofSci. &Tech,Nanjing210007,China)

In the paper, the linear distribution of horizontal stress is considered based on the layer structure method, and the deep underground cavern structure elastic solution is obtained by the usage of elasticity mechanics. The calculation result is closer to the actual situation of engineering in deep underground with linear horizontal stress.

circular cavity, stress function, horizontal stress, elastic solution

1009-6825(2016)08-0042-02

2016-01-07

尤业超(1992- )，男，在读硕士；韩阳(1991- )，男，在读硕士；卞少帅(1990- )，男，在读硕士

TU318

A