砌体结构烟囱筒体风荷载作用下的可靠度分析★

金　涛　上官子昌 *　董榅键

(大连海洋大学海洋与土木工程学院，辽宁 大连　116023)



·结构·抗震·

砌体结构烟囱筒体风荷载作用下的可靠度分析★

金涛上官子昌 *董榅键

(大连海洋大学海洋与土木工程学院，辽宁 大连116023)

研究了在风荷载的作用下得到砌体结构烟囱筒体受压破坏极限状态方程，以30 m高烟囱为例，考虑荷载效应基本组合，提出了采用蒙特卡罗法(Monte Carlo Method)并结合Matlab编程计算可靠度的方法，可供参考。

烟囱，可靠度，蒙特卡罗法

0　引言

砌体结构烟囱是目前我国排放烟气或废气的主要高耸构筑物[1]，由于砌体结构材料来源广泛，造价低廉，施工简单，目前在我国各种烟囱中砌体结构烟囱是比较常见的一种构筑物，如图1所示。而在非地震区，风荷载为烟囱结构设计的主要水平荷载。由于烟囱特殊的体型特征，需要考虑不同情况下的可靠度指标来保证结构的工作状态。

1　砌体结构烟囱的基本假设

在风荷载的作用下，砌体结构烟囱的应力和应变值应在变形的允许范围内，烟囱采用烧结普通砖砌筑的筒体结构，壁厚在高度方向均匀变化，烟囱形状及截面和壁厚剖面图如图2和图3所示。

2　砌体结构烟囱在风荷载作用下的受力分析

对于大部分地区的烟囱受到的主要水平荷载为风荷载，而雨荷载和雪荷载对烟囱的作用可以忽略不计。而受到的主要竖向荷载为砌体结构烟囱的自重，它们是烟囱的主要受力荷载。

为简化计算，采用以下基本假定：1)砌体为弹性材料；2)砌体的刚度、强度不随时间变化；3)标准高度的年最大平均风速为伯努利实验。

2.1水平风荷载引起砌体结构烟囱底部的弯矩M

基本风压：水平风荷载的基准压力，现行规范按当地空旷平坦地面上10 m高度处10 min平均的风速观测数据，经概率统计得出50年一遇最大值来确定的风速，再考虑当地相应的空气密度，按贝努利(Bernoulli)公式确定的风压。

垂直于建筑物表面上的风荷载标准值，应按下列规定确定[2]：

计算主要受力结构时，应按式(1)计算：

ωk=βZμSμZω0

(1)

其中，βZ为高度Z处的风振系数；μS为风荷载体型系数；μZ为风压高度变化系数；ω0为基本风压，kN/m2。

烟囱在风荷载作用下的计算简图如图3所示，设烟囱的底部直径为D，烟囱的高度为H，由式(1)可得垂直于烟囱表面每段(H/3)高度上风荷载标准值的大小为(i=1，2…)：

Fi=βZμSiμZiω0DiLi

(2)

其中，βZ为高度Z处的风振系数；μSi为各点处风荷载体型系数；μZi为各点处风压高度变化系数；ω0为基本风压，kN/m2；Li为各点处等效受荷高度；Di为烟囱各段截面直径。

由上述式(2)得各点处等效风荷载在烟囱底部产生的总弯矩M标准值解析式如下：

(3)

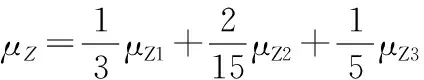
2.2竖向力作用下烟囱底部轴向压力

设g为重力加速度，取g=10m2/s，在竖向自重力的作用下砌体结构烟囱底部的轴向压力标准值为：

N=6.8γA0H

(4)

其中，A0为烟囱底部截面的面积，m2；H为烟囱的高度，m；γ为砌体的容重，kN/m3。

2.3烟囱底部外径的计算公式

设d为烟囱底部的内径，m；c为烟囱底部的壁厚，m；则烟囱底部的外径D为：

D=d+2c

(5)

3　结构可靠度分析

结构可靠度是指在规定的时间内、规定的条件下完成预定功能的能力。计算结构可靠度的方法有很多种，本文中采用计算精度比较高的蒙特卡罗法(Monte Carlo Method)计算结构的可靠度，蒙特卡罗法根据随机变量的分布函数选取N次随机数输入到分析中，计算功能函数式的值，假如失效的次数为n，因此可以用n/N来表示一个安全系数a。用Z=g(X1，X2，X3，…，Xn)来描述结构的工作状态，则Z称为结构的功能函数。

现以R表示结构抵抗外力的荷载，S表示作用在结构上的荷载，则结构的功能函数表达式为：Z=g(R，S)=R-S，由上式可知当RS(Z>0)时处于可靠状态。

3.2可靠度指标β的确定

3.3砌体结构烟囱功能函数方程

砌体结构烟囱在竖向自重力和水平力风荷载共同作用下，水平截面极限承载能力应按下列公式计算[3]：

N≤φfA

(6)

(7)

β=hd/d

(8)

其中，N为在竖向力自重的作用下砌体结构烟囱底部的轴向压力设计值，N；A为计算截面面积，m2；φ为高径比及轴向力偏心距对承载力的影响系数；β为计算截面以上筒壁高径比；hd为计算截面至筒壁顶端的高度，m；d为烟囱计算截面直径，m；e0为在风荷载设计值作用下，轴向力至截面重心的偏心距，m；α为与砂浆强度等级有关的系数，当砂浆等级不小于M5时，α=0.001 5；当砂浆强度等级为M2.5时，α=0.002 0；f为砌体抗压强度设计值，由式(9)确定：

对工件裂纹形貌检查，选取开裂处切取一个单齿，暴露裂纹面，裂纹面宏观检验，裂纹面形貌一致，呈现应力型裂纹形貌，如图3所示。

(9)

其中，fm为砌体的强度平均值；δf为砌体强度变异系数；γf为砌体结构的材料性能分项系数，一般情况下，宜按施工质量控制等级为B级考虑，取1.60。

我国现行砌体结构规范采用的砌体强度平均值公式为：

(10)

其中，fm为砌体抗压强度平均值，MPa；f1为块体(砖、石、砌体)抗压强度等级或平均值，MPa；f2为砂浆抗压强度平均值，MPa；α为考虑砌块高度对砌体强度的修正系数；k1为块体类别和块体砌筑方法的修正系数；k2为砂浆强度影响对砌体抗压强度的修正系数。

以块体(砖、石、砌体)抗压强度等级或平均值f1和砂浆抗压强度平均值f2、基本风压ω0、砌体的容重r以及烟囱底部内径d和壁厚c为随机变量。结合可靠度理论，因此推导出结构功能函数表达式为：

Z=g(R,S)=g(f,ω0,r)=φfA-N

(11)

取自重和风荷载的分项系数均为1，将式(3)～式(10)代入式(11)得：

(12)

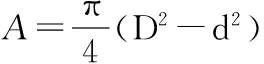
(13)

(14)

其中，H为已知常数,在本文中H=30 m。

4　砌体结构烟囱在风荷载作用下的可靠度算例

4.1随机变量统计参数

算例：以30 m高烟囱为例，根据有关规范规定[4]：对于随机变量基本风压标准值ω0，新疆哈密地区30年一遇的基本风压ω0=660 kN/m2。在设计基准期100年时，μω0=961 kN/m2，σω0=168 N/m2。查阅有关文献可知MU30烧结普通砖和M10砂浆的抗压强度平均值服从指数分布，分别为λ(f1)和λ(f2)，通过大量实验可知：μf1=30 MPa，σf1=1.95 MPa，μf2=10 MPa，σf2=1.16 MPa。烧结普通砖的容重γ服从N(μγ，σγ)的正态分布，μγ=1 800 kg/m3，σγ=116 kg/m3。砌体强度变异系数δf=0.10和其他各系数的取值为：砌块高度对砌体强度的修正系数α=0.5，块体类别和块体砌筑方法的修正系数k1=0.78，砂浆强度影响对砌体抗压强度的修正系数k2=1.0，风荷载体形系数μS=0.8，风振系数βZ=1.0，计算可得μZ=0.49。通过现场实地测量，得到30 m高烟囱底部的内径d和壁厚c也近似服从N(μd，σd)和N(μc，σc)的正态分布，其中μd=3 m，μc=0.5 m，σd=σc=0.058 m。

4.2运用蒙特卡罗方法(Monte Carlo Method)

用蒙特卡罗法的关键是要产生随机数，然后根据随机变量的概率分布进行随机抽样。xi(i=1,2,3,…,n)进行N次随机抽样，得到每一个变量的样本值xi(i=1,2,3,…,n),用所得样本值xi(i=1,2,3,…,n)计算功能函数Z=g(R，S)的值，若总共进行了N次，如果Z<0则结构失效一次，记录失效的次数记为nf，则结构失效的概率为:

(15)

已知算例中的基本风压标准值ω0近似服从λ(ω0)的指数分布，本文中的试验次数为2万次。Matlab有很大的功能，能直接产生服从各相应概率分布函数的随机变量数组[5]，如正态分布、指数分布等，可直接产生随机变量xi(i=1,2,3,…,n)以代入功能函数中。

4.3计算结果

通过运用Matlab编程软件并结合式(5)，式(12)～式(15)计算该算例的可靠度β=3.8，可以看出，此算例砌体结构烟囱的可靠度指标满足现行砌体结构设计规范规定的建筑结构安全等级为二级，结构构件承载力极限状态的可靠度指标(脆性破坏)β≥3.7的要求。

5　结语

1)本文以砌体受压破坏为极限状态，得到烟囱在水平风荷载作用下水平截面极限承载能力可靠度的计算过程。

2)以30 m高烟囱为例，通过可靠度计算，用烧结普通砖砌筑的烟囱在风荷载作用下的可靠度指标β≥3.7，满足现行规范中的要求。

3)用Matlab编程软件实现蒙特卡罗方法(Monte Carlo Method)分析结构可靠度比其他分析方法更简单适用，此方法的普遍适用性使其成为当今研究结构可靠度的很好方法，此方法将来能在结构可靠度计算中发挥巨大的作用。

[1]GB 50051—2013，烟囱设计规范[S].

[2]GB 50009—2012，建筑结构荷载规范[S].

[3]GB 50003—2011，砌体结构设计规范[S].

[4]卫军，周锡武，张晓霞，等.超高太阳能烟囱结构可靠性计算分析[J].广州城市职业学院学报,2007,1(11):80-86.

[5]薛定宇，陈阳泉.高等应用数学问题的MATLAB求解[M].北京：清华大学出版社,2013:47-72.

Reliability analysis of masonry structure chimney body under wind loads★

Jin TaoShangguan Zichang*Dong Wenjian

(OceanandCivilEngineeringInstitute,DalianOceanUniversity,Dalian116023,China)

Research under the wind load are deduce the concrete compression failure equation of masonry structure chimney body. Finally the paper points out a method that using Matlab programs to calculate a series of structure reliability of a 30 m-example chimney according to the Monte Carlo Method the influence basic combination of action effects are indicated, for reference.

chimney body, reliability, Monte Carlo Method

1009-6825(2016)08-0035-03

2016-01-05★：蓝色学科(项目编号：34/100713025)

金涛(1987- )，男，在读硕士；董榅键(1992- )，男，在读硕士

上官子昌(1959- )，男，博士，教授，国家一级结构工程师

TU362

A