乳腺肿瘤同伦LM算法EIT图像重建
秦伟刚,王 超
(1. 天津大学电气与自动化工程学院,天津 300072;2. 天津工业大学电气工程与自动化学院,天津 300387)
乳腺肿瘤同伦LM算法EIT图像重建
秦伟刚1,2,王 超1
(1. 天津大学电气与自动化工程学院,天津 300072;2. 天津工业大学电气工程与自动化学院,天津 300387)
将同伦延拓方法与Levenberg-Marquardt(LM)迭代算法相结合,对不同的乳腺肿瘤模型进行图像重建,并与LM算法进行比较.在不同迭代初始值下,同伦LM算法与LM算法的平均电导率相对误差相比,最优值能降低接近7%,,运行时间最大能减少46%,的计算开销,电压相对误差要优于LM算法7%,以上.实验结果表明,同伦LM算法比LM算法能重建更好的图像,提高了重建图像的精度和收敛速度.
电阻抗层析成像;同伦延拓法;Levenberg-Marquardt算法
与其他肿瘤相比,女性乳腺肿瘤的发病率最高[1].乳腺肿瘤检测方法主要分为两大类:侵入式和非侵入式.在非侵入式方法中,电阻抗层析成像(electrical impedance tomography,EIT)是一种新的无损伤功能成像技术[2],在生物医学工程领域被应用于如乳腺肿瘤检测[3]、肺通气功能检测[4-5]和脑功能检测[6]等的临床研究中.由此可见,EIT可以用来研究病变组织的变化情况,对其成像研究仍然是有价值的.
通常,EIT逆问题具有非线性和欠定性,因此迭代算法被广泛采用,如正则化牛顿法、Levenberg-Marquardt(LM)法和Landweber法[7-9].这些图像重构算法在一定约束条件下都可以使求解问题收敛,但这些算法都是局部收敛的 .
LM算法是结合二次收敛牛顿法与梯度下降法的一种非线性优化迭代方法,在EIT逆问题求解中获得了很多应用[10].对LM算法来说,如果初始值不在收敛域内,全局最小值就很难获得.许秋平[11]使用LM算法求解非线性方程,虽然可以解决系数矩阵奇异的问题,但当选取的初始值与真实值相距较远时,出现不收敛的情况.Kleefeld等[12]将LM算法用于参数估计问题,由于实际的电导率未知,初始值的选取较为困难.
同伦延拓法(homotopy continuation method)是一种解决非线性逆问题的强有力工具,对初值要求十分宽松,且具有全局收敛特性[13-14],可以被用于EIT逆问题的求解[15],并且与其他方法结合能进一步提高计算效率.吴焕丽等[16]将牛顿法和同伦方法进行结合,Fu等[17]提出了一种Tikhonov正则化-同伦方法,Wu[18]设计了一种同伦Newton-Raphson方法,提高了收敛速度和计算精度.
由上可知,用LM算法来解非线性方程的解,要求初始值应接近真实解,才能更好地收敛到真实解,实际上真实解并不知道.本文基于同伦方法和LM算法,给出了一种同伦LM算法(称为HLM算法),对不同乳腺肿瘤模型进行图像重建.首先利用同伦延拓方法为EIT逆问题求解的LM算法产生一个较好的迭代初始值,然后再通过LM迭代算法来收敛到全局最优解,并讨论了平均电导率相对误差、运行时间和电压相对误差随初始值的变化情况.
1 EIT数学描述
假设所研究的敏感场为似稳场,内部无电流源,根据Maxwell方程,在敏感场内满足Poisson方程

式中:σ为电导率分布;φ为敏感域内的电势分布.
在施加电流的电极上满足
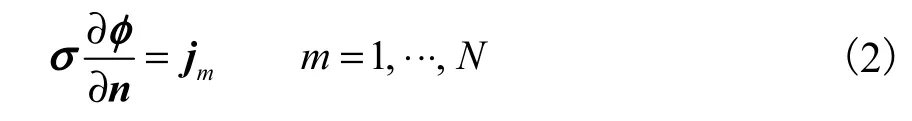
式中:jm为由电极注入的电流密度;n为外方向单位矢量;N为电极数.
在测量电极上满足

当媒质各向同性、电导率σ均匀分布时,方程(1)变为Laplace方程,即

2 EIT逆问题求解算法
2.1LM算法
EIT逆问题可表示为非线性方程

或者最小二乘问题,即将计算电压和测量电压的误差2范数作为代价函数,记R(σ)=f(σ)-U ,则

式中:f(σ)表示注入电流后,对应电导率分布σ的边界计算电压;U表示边界测量电压;表示欧几里德范数.
令代价函数

要满足式(7),可通过标准Gauss-Newton法进行迭代,即

式中:k为迭代数,k=1,2,…;J为Jacobian矩阵;JTJ称为Hessian矩阵,且为对称阵;M为有限元剖分单元数.
为克服Hessian矩阵的严重病态性,以及避免步长过大,重新将代价函数写为

求式(10)对σk+1的极小点,可得
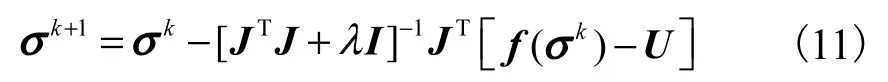
式(11)就是所要求解的LM算法的迭代公式,其中λ>0称为阻尼因子,I为单位矩阵.当λ较大时LM算法接近于梯度下降法,当λ较小时接近于Gauss-Newton法.
2.2同伦延拓法
由于LM算法具有局部收敛性,同伦延拓法具有全局收敛性,且对初始值不敏感.构造定点同伦方程[19]为
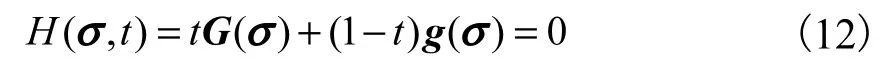
式中t为同伦参数,t∈[0,1].式(12)满足2个边界条件

式中g(σ)为一简单函数,与G(σ)为同伦映射.
2.3HLM算法
定义泛函

为了寻求式(14)的解,让G(σ)表示为T(σ)的一阶导数,即

同伦是拓扑学中的基本概念,定点同伦的表达式可写为

式中σ0表示初始电导率,它也是式(17)的解.
同伦方程(16)的解为σ随t由0到1变化的一条连续曲线.根据萨德(Sard)定理,同伦方程对初始值的选择几乎都有解,不可解的测度为零[20].
为简化计算,方程(16)中t∈[0,1]取等间隔分布tk=k/K,同伦LM优化算法的迭代公式为

当迭代次数小于K时,按照式(18)进行迭代;大于K时,按照式(19)进行迭代.目的是经过式(18)的计算为式(19)寻求一个较好的初值,最终经式(19)收敛到真实解.
由于逆问题中Jacobian矩阵的条件数很大,为提高成像质量和收敛速度,对参数λ采用可调模式,初始值定义为

式中τ根据拇指规则[20]确定,取τ=0.1.
为解决同伦算法计算效率不高的问题,此处对式(18)中λ的取值为

式(19)中λ的取值为
3 仿真实验和结果
本文采用16电极结构,等间隔排列在敏感场的外表面,采取“相邻电流激励-相邻电压测量”模式.根据有限元法对其进行三角元网格剖分,进行图像重建,剖分结果包含1,024个三角元和609个节点.
实验运行在Inter Core2 CPU2.4,GHz、RAM 2,GB的计算机上.以计算电压和测量电压差值的2范数作为停止迭代条件,允许误差大小设为0.000,01,最大迭代次数设为30.根据恶性肿瘤和正常组织的差异性,病变组织的电导率要高于正常组织,文中设背景电导率为1,S/m,目标电导率为5,S/m,给出了4种不同乳腺肿瘤模型分布,如图1~图4所示.上述算法通过MATLAB实现,图1~图4中第2列为LM算法重建的灰度图像,第3列为HLM算法重建的灰度图像.

图1 模型分布1及其图像重建Fig.1 Model distribution 1 and its image reconstruction

图2 模型分布2及其图像重建Fig.2 Model distribution 2 and its image reconstruction

图3 模型分布3及其图像重建Fig.3 Model distribution 3 and its image reconstruction

图4 模型分布4及其图像重建Fig.4 Model distribution 4 and its image reconstruction
4 分析和讨论
为定量评价重建图像的质量,定义平均电导率相对误差

式中:σc为计算电导率分布;σr为实际电导率分布.定义参数evr表示电压相对误差,即
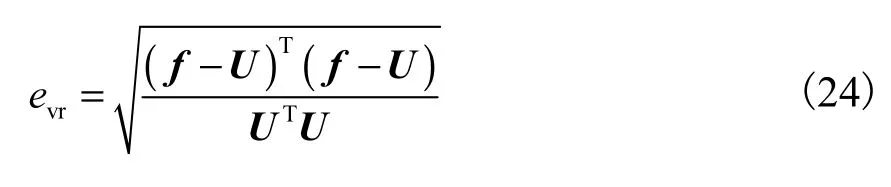
由于同伦方法计算效率不高,针对不同的乳腺肿瘤模型,图5给出了同伦法计算的不同初始电导率时的电压相对误差.
接下来,通过LM算法和HLM算法对平均电导率相对误差进行了对比,图6描述了两种算法在不同初始电导率时的计算结果.结果显示,HLM算法计算的电导率相对误差要小于LM算法的电导率相对误差,并且两种算法得到结果的变化趋势是一致的,也说明HLM算法提高了重建图像的精度.
虽然同伦方法可以扩大算法的收敛域,但是并没有消除对初值的依赖性,从图5的结果来看,不同的初值下,前期迭代的电压相对误差变化较大,随着迭代次数增加,电压相对误差变化一直处于下降的趋势.对同一种模型分布来说,不同的初值情况,随着迭代次数的增加,电压相对误差数值的下降也是比较明显的.从图6的结果来看,不同的模型分布取不同的初值迭代时,HLM算法与LM算法的平均电导率相对误差相比,最大能降低接近7%,.实验发现,对于HLM算法来说,不同的初值,从同伦法切换到LM算法的迭代时刻不同,目的是为LM算法提供一个较好的初始值,这也说明引入同伦法后,迭代算法仍然是稳定的.
为进一步说明HLM算法的有效性,分别取不同电导率迭代初始值,利用LM算法和HLM算法计算不同模型分布的运行时间,如图7所示.可以发现,使用HLM算法计算的运行时间比LM算法计算的运行时间有所减少,最大能减少46%,的计算开销,这也表明HLM算法进一步提高了重建图像的收敛速度.
最后,对两种算法的电压相对误差进行了比较,如图8所示.同样,HLM算法计算的电压相对误差明显要优于LM算法7%,以上,也体现了HLM算法优于LM算法.

图5 同伦法计算的不同初始电导率时的电压相对误差Fig.5 Relative errors of the voltage calculated by homotopy method for different initial conductivities

图6 LM算法和HLM算法计算的平均电导率相对误差Fig.6 Relative errors of the average conductivity calcu-lated by LM and HLM algorithms
从上述结果可以看出,与LM算法相比,HLM算法能提高图像重建的精度和收敛速度,能获得更好的图像重建结果.
另一方面,由于EIT逆问题的软场特性,即灵敏场分布随着电导率的变化而改变,这种非线性增加了图像重建的难度.文中HLM算法克服了LM算法的缺点,使得重建图像更加稳定.当然,为了获得更精确的解,像电极数目、电极形状以及网格剖分的数量都需要进一步的综合考虑,以提高敏感场的灵敏度,为EIT逆问题求解提供可靠、有效的测量信息.
5 结 语
文中给出了一种优化的图像重建迭代算法——HLM算法,对不同的乳腺肿瘤模型进行研究,利用具有大范围收敛域的同伦延拓法进行电导率修正,然后作为初始值代入LM算法进行迭代,直至最后收敛,说明了HLM算法的可行性和有效性.从平均电导率相对误差、运行时间和电压相对误差来看,HLM算法提高了重建图像的精度和收敛速度.另外,提高敏感场的灵敏度和基于阻抗成像算法仍然是研究的重点,并且值得进一步探索.
[1] Siegel R,Ma J M,Zou Z H,et al. Cancer statistics CA:A cancer[J]. Journal for Clinicians,2014,64:9-29.
[2] Mamatjan Y,Grychtol B,Gaggero P,et al. Evaluation and real-time monitoring of data quality in electrical impedance tomography[J]. IEEE Transactions on Medical Imaging,2013,32(11):1997-2005.
[3] Kantartzis P,Abdi M,Liatsis P. Stimulation and measurement patterns versus prior information for fast 3D EIT:A breast screening case study[J]. Signal Processing,2013,93:2838-2850.
[4] Camporota L,Smith J,Barrett N,et al. Assessment of regional lung mechanics with electrical impedance tomography can determine the requirement for ECMO in patients with severe ARDS[J]. Intensive Care Med,2012,38:2086-2087.
[5] 王 超,白瑞峰,魏艺明,等. 基于小波变换肺部气血阻抗分离及能量分析[J]. 天津大学学报:自然科学与工程技术版,2014,47(3):195-199. Wang Chao,Bai Ruifeng,Wei Yiming,et al. Separation of pulmonary gas-blood bio-impedance and energy analysis based on wavelet transformation[J]. Journal of Tianjin University:Science and Technology,2014,47(3):195-199(in Chinese).
[6] Bera T K,Biswas S K,Rajan K,et al. Projection error propagation-based regularization(PEPR)method for resistivity reconstruction in electrical impedance tomography(EIT)[J]. Measurement,2014,49:329-350.
[7] Wang C,He X R,Bai R F. Trackability evaluation of reconstruction algorithms to the change of measured objects in electrical tomography[J]. Physiological Measurement,2014,35:583-596.
[8] Kanzow C,Yamashita N,Fukushima M. Levenberg-Marquardt methods with strong local convergence properties for solving nonlinear equations with convex constraints[J]. Journal of Computational and Applied Mathematics,2005,173:321-343.
[9] Wang H X,Wang C,Yin W L. A pre-iteration method for the inverse problem in electrical impedance tomography[J]. IEEE Trans on Instrum Meas,2004,53:1093-1096.
[10] Barra L P S,Telles J C F. A geometric inverse problem identification procedure for detection of cavities[J]. Engineering Analysis with Boundary Elements,2013,37:1401-1407.
[11] 许秋平. 电力调度系统中拓扑分析与潮流计算方法的研究[D]. 济南:山东大学数学学院,2011. Xu Qiuping. A Study of Topological Analysis and Flow Calculation in Power System Dispatching[D]. Jinan:School of Mathematics,Shandong University,2011(in Chinese).
[12] Kleefeld A,Reißel M. The Levenberg-Marquardt method applied to a parameter estimation problem arising from electrical resistivity tomography[J]. Applied Mathematics and Computation,2011,217:4490-4501.
[13] 黄象鼎,曾钟钢,马亚南. 非线性数值分析的理论与方法[M]. 武汉:武汉大学出版社,2004. Huang Xiangding,Zeng Zhonggang,Ma Yanan. The Theory and Method for Nonlinear Numerical Analysis[M]. Wuhan:Wuhan University Press,2004(in Chinese).
[14] Huang Q Q,Zhu Z B,Wang X L. A predictor-corrector algorithm combined conjugate gradient with homotopy interior point for general nonlinear programming [J]. Applied Mathematics and Computation,2013,219:4379-4386.
[15] Liu S,Lei J,Li Z H,et al. Generalized flow pattern image reconstruction algorithm for electrical capacitance tomography[J]. Nuclear Engineering and Design,2011,241:1970-1980.
[16] 吴焕丽,徐桂芝,张 帅,等. 基于圆柱模型的三维电阻抗成像问题研究[J]. 山东大学学报:理学版,2009,44(5):45-48. Wu Huanli,Xu Guizhi,Zhang Shuai,et al. Research of the three-dimensional electrical impedance tomography based on the cylinder model [J]. Journal of Shandong University:Natural Science,2009,44(5):45-48(in Chinese).
[17] Fu H S,Han B. Tikhonov regulation-homotopy method for electrical impedance tomography[J]. Journal of Natural Science of Heilongjiang University,2011,28(3):319-323.
[18] Wu T M. Solving the nonlinear equations by the Newtonhomotopy continuation method with adjustable auxiliary homotopy function[J]. Applied Mathematics and Computation,2006,173:383-388.
[19] 徐桂芝,李 颖,杨 硕,等. 生物医学电阻抗成像技术[M]. 北京:机械工业出版社,2010. Xu Guizhi,Li Ying,Yang Shuo,et al. Electrical Impedance Tomography in Biomedical Engineering[M]. Beijing:China Machine Press,2010(in Chinese).
[20] Madson K,Nielsen H B,Tingleff O. Methods for Non-Linear Least Squares Problems(Informatics and Mathematical Modelling)[M]. 2nd ed.Copenhagen,Denmark:Technical University of Denmark,2004.
(责任编辑:孙立华)
Image Reconstruction of Breast Tumors Using Homotopy LM Algorithm in Electrical Impedance Tomography
Qin Weigang1,2,Wang Chao1
(1.School of Electrical Engineering and Automation,Tianjin University,Tianjin 300072,China;2.School of Electrical Engineering and Automation,Tianjin Polytechnic University,Tianjin 300387,China)
A homotopy Levenberg-Marquardt(HLM)algorithm,which is the combination of homotopy continuation method and Levenberg-Marquardt(LM)algorithm,was presented.The reconstructed images of different breast tumor models were acquired by HLM algorithm and compared with those by LM algorithm.The relative errors of the average conductivity were obtained by means of HLM algorithm and LM algorithm.The optimal value of the relative errors of the average conductivity by HLM algorithm was reduced by nearly 7 percent for different initial values.The best running time and the relative errors of the voltage are decreased by 46 percent and 7 percent respectively.The results show that the better images are reconstructed by HLM algorithm,and the accuracy and convergence rate are improved.
electrical impedance tomography(EIT);homotopy continuation method;Levenberg-Marquardt(LM)algorithm
R318
A
0493-2137(2016)05-0506-07
10.11784/tdxbz201504037
2015-04-10;
2015-08-26.
国家自然科学基金重点资助项目(50937005).
秦伟刚(1978—),男,博士研究生,qinweigang@tjpu.edu.cn.
王 超,wangchao@tju.edu.cn.
网络出版时间:2015-11-11. 网络出版地址:http://www.cnki.net/kcms/detail/12.1127.N.20151111.1802.010.html.

