边界应力对石墨烯翘曲的影响

张海正, 师明星

(西南交通大学力学与工程学院, 成都　610031)



边界应力对石墨烯翘曲的影响

张海正, 师明星

(西南交通大学力学与工程学院, 成都610031)

对于边界应力引起的石墨烯薄膜边界翘曲问题，分别建立了理想边界模型和真实边界模型来分析边界尺寸对翘曲形貌的影响。通过建立弹性薄壳模型，将边界处理成只具有面积而没有几何尺寸的理想梁模型以及具有真实尺寸的真实边界壳模型，然后进行理论分析来确定石墨烯薄膜边界翘曲时的尺度关系(即翘曲波形的波长、腹向衰减表征尺度以及面外翘曲幅值)。理论分析发现，边界宽度的变化对石墨烯薄膜的能量、翘曲幅值及腹向衰减尺度的影响显著，且当边界宽度为0.1 nm时，总应变能有最小极值点出现在波长为7 nm左右，该发现与原子模拟研究所得结果基本一致；同时发现，石墨烯翘曲幅值在边界宽度为0.1 nm时幅值达到最大，腹向衰减尺度随边界宽度在边界宽度为0.1 nm时衰减得最快。

石墨烯；边界应力；边界宽度；边界翘曲；薄壳理论

引　言

石墨烯是由单层碳原子通过共价键链接按照六方环状对称结构排列而成。继2004年英国曼彻斯特大学的两位科学家发现了石墨烯以后[1]，其优异的性能和独特的二维结构一直都是众人研究和讨论的焦点问题。石墨烯中每个碳原子通过很强的键σ(自然界中最强的化学键)与其他的三个碳原子相连接，这些很强的碳-碳键使石墨烯片层具有极其优异的力学性质和结构刚性。碳原子的四个价电子，每个碳原子都贡献一个未成键的π电子，这些π电子垂直于平面方向，可形成π轨道，在晶体中自由移动，赋予石墨烯良好的导电性。而这些面外离位的π键与相邻层内的键的作用力远小于σ键，故其层间作用力远远小于层内作用力，使得石墨层间很容易分离，形成单层的石墨烯。

由于其独特的二维结构以及优异的晶体品质，石墨烯具有十分优异的电学、热学、磁学和力学性能[2-8]。石墨烯作为已知的世上最薄、最坚硬的纳米材料，其杨氏模量可达到1.1 TPa(是钢的100多倍)，透光率约为97.7%[9]，几乎完全透明，并拥有气体完全不渗透性[10]，热系数高达5300 W/m·k，高于碳纳米管，常温下其电子迁移率超过15 000 cm2/V·S，比纳米碳管或硅晶体高[11]，而电阻率只约10-3Ω/m，比铜或银更低，为世上电阻率最小的材料。使其在纳电子器件、高灵敏传感器、透明导电薄膜、功能复合材料、储能、催化等领域有着广阔的应用前景[12-13]。

研究表明，在没有热影响的情况下(绝对温度为零)，由于边界应力的存在，独立的石墨烯薄膜的边界仍表现出不稳定性，边界的原子结构对石墨烯的边界形貌产生影响。Shenoy等[14]基于有限元分析和原子模拟的研究发现，手扶椅形(armchair)边界和锯齿形(zigzag)边界均会产生边界压应力，边界压应力的存在会使石墨烯薄膜产生翘曲现象，同时发现锯齿形边界的翘曲幅度大于手扶椅边界的翘曲幅度。

Reddy等[15]通过建立弹性薄壳模型来分析石墨烯薄膜边界翘曲时的尺度关系(即翘曲波形的波长、腹向衰减表征尺度以及面外翘曲高度)。在其模型的理论分析中，边界被简化处理成只具有面积而没有几何尺寸的理想梁模型。然而，这并不能全面表征真实的石墨烯薄膜边界原子结构情况。真实的石墨烯薄膜边界附近原子结构与内部不同，即石墨烯薄膜的实际边界存在一定的几何宽度。因而，边界宽度对翘曲形貌的影响，该在研究中得到重视。文献检索显示，边界宽度对石墨烯翘曲的影响还没有被研究过。进行该方面的研究，将有助于了解石墨烯薄膜翘曲形貌中边界宽度和其它尺度之间应满足的关系，丰富石墨烯薄膜的研究内容。

1　石墨烯力学参数的确定

原子力纳米压痕实验和原子力显微镜等先进的实验技术被广泛用于测量石墨烯的力学的相关参数。Lee C等[7]利用原子力显微镜压痕技术首次分析了石墨烯的弹性模量和断裂强度，得出石墨烯的杨氏模量为(1.0±0.1)TPa，理想强度为(130±10)GPa(假定石墨烯的厚度为0.335 nm);Gomez-Navarro C等[16]通过化学的方法制备单层石墨烯，然后利用原子力显微镜测试其弹性性能，得到石墨烯杨氏模量为(0.25±0.15)TPa(假设石墨烯的厚度为1 nm)。Poot M等[17]通过原子力纳米压痕实验测试了石墨烯的弯曲刚度和应力特性，二者被证实随薄膜厚度的增加而增加。

然而，由于石墨烯特殊的原子量级厚度的平面层状二维结构，用实验的方法对石墨烯力学性能进行测试仍然难度较大。一方面是由于高质量石墨烯材料的制备存在较大难度，另一方面是由于可有效使用的实验设备和技术较少，且测量数据的精度不易保证。理论分析方面，目前尚未出现较成熟的纳米尺度的力学理论框架，很多研究者是基于连续介质理论分析方法研究石墨烯等纳米尺度材料的力学性能[18-25]。

考虑到石墨烯边界弹性模量是随边界宽度的变化而变化，当石墨烯边界宽度趋近于零时，边界弹性模量趋近于一个定值；而当边界宽度趋近于无穷大时边界弹性模量应与石墨烯内部弹性模量有如下关系：

Ee=Eb·b

(1)

表1　石墨烯薄膜参数表

2　两种理论分析模型

2.1理想边界模型

如图1所示，在理想边界模型中，将边界处理成具有面积而没有具体几何尺寸的梁模型。表征边界尺度效应的边界宽度可以改变，厚度不变，从而边界的面积会变化，这些变化会体现到边界的弹性模量和边界应力当中。

图1理想边界模型

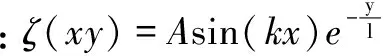
(2)

(3)

(4)

相应地，理想边界时系统的应变能为：

(5)

其中，石墨烯薄膜内部应变能密度表达式为：

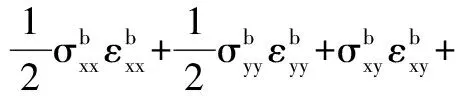
(6)

边界应变能密度为：

(7)

得到理想边界模型总能量表达式为：

Π=Πbulk+Πedge+Πinternal-stress

(8)

其中:Πbulk、Πedge、Πinternal lstress表达式见附录。

根据最小势能原理，石墨烯纳米带边界发生翘曲时总势能应满足如下方程：

(9)

(10)

联立(8)、(9)两个方程，组成非线性方程组，用以确定翘曲变形参数间的关系。

2.2真实边界模型

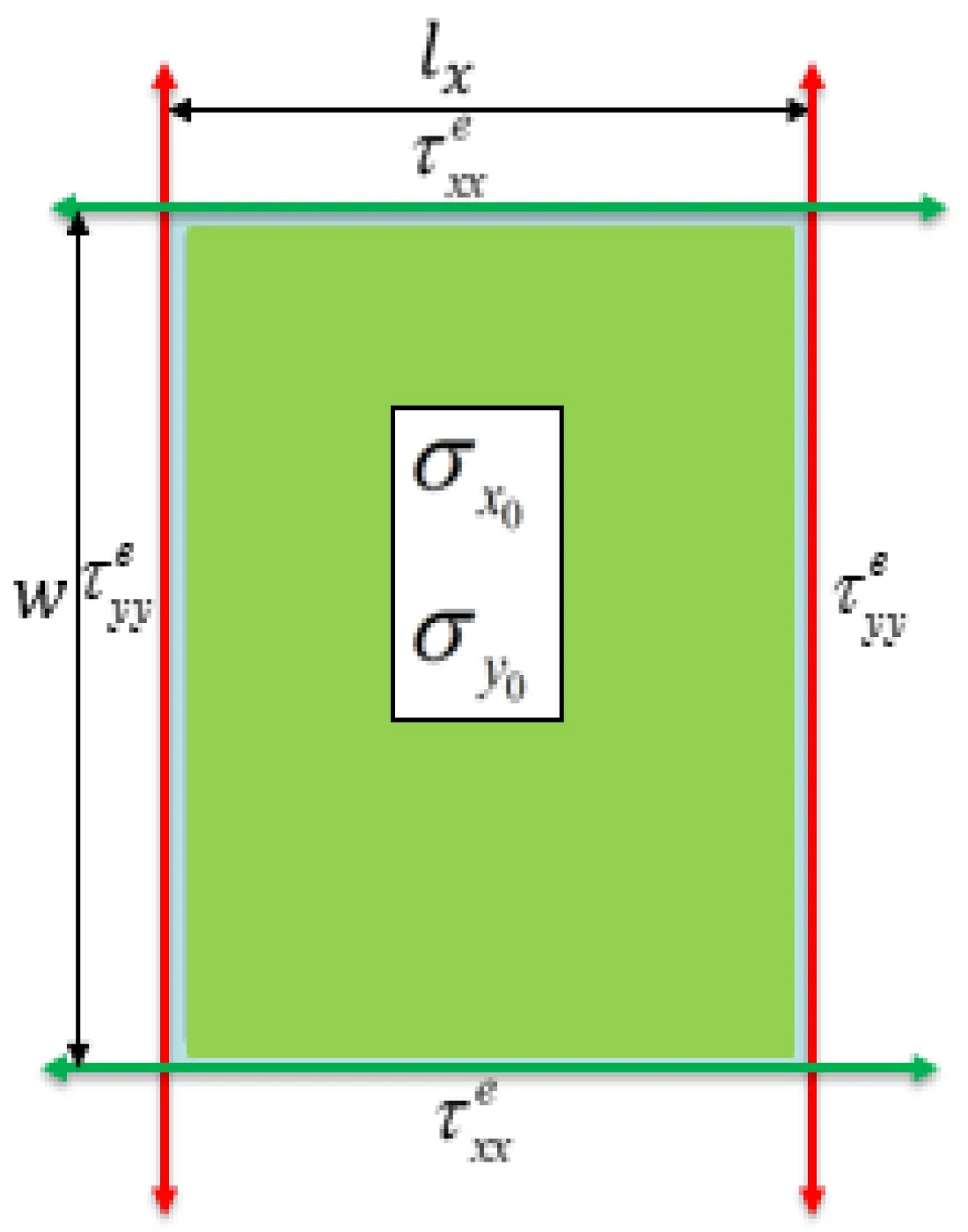
图2真实边界模型示意图

同样引入石墨烯薄膜面外翘曲函数为：，石墨烯薄膜内部和边界的应变都由式(2)～式(3)给出。真实边界模型时系统的应变能为：

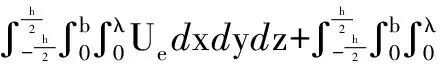
(11)

其中，石墨烯薄膜内部应变能密度由式(6)给出，边界应变能密度则为：

(12)

这样得到真实边界模型总能量表达式为：

(13)

根据最小势能原理，总应变能分别对翘曲幅值及腹向衰减尺度求偏导，可得：

(14)

(15)

联立(14)、(15)两个方程，可以得到表征石墨烯边界翘曲的真实边界模型的非线性方程组。求解此方程组，可以确定表征翘曲变形的参数与几何尺寸(边界宽度)之间的关系。

对于上面得到的两种模型的方程组式(9)与式(10)、式(14)与式(15)，用Matlab数值计算分析软件进行求解。结合分子动力学模拟分析结果，给定初始翘曲波长时，求解方程组来确定翘曲幅度和翘曲向腹内衰减幅度的大小。

3　数值结果与讨论

3.1理想边界模型

在理想边界模型中，对于具有不同宽度边界的石墨烯纳米带，其发生不同波长翘曲时的应变能如图3所示。容易看出，在边界宽度b=0.1nm时，总应变能曲线有明显极值点，在λ=7附近。而在边界宽度b≥0.2时，总能量明显比b=0.1 nm的情形要高很多，并且无明显极值点出现，相比之下边界宽度b=0.1 nm时总能量最小，石墨烯薄膜整体相对最为稳定。

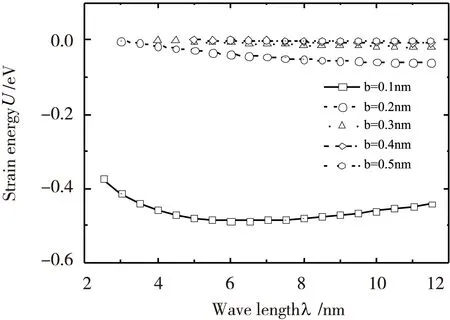
图3理想边界模型应变能变化曲线图

图4为薄膜翘曲幅值随翘曲波长的变化曲线图，从图中可以看出翘曲幅值随翘曲波长的增加呈增加趋势，且增加速度逐渐减缓；同时，在翘曲波长一定时，翘曲幅值随边界宽度增加而明显减小，相比之下边界宽度b=0.1 nm时，翘曲幅值达到最大值。

图4理想边界翘曲幅值变化曲线图

图5为翘曲腹向衰减尺度随翘曲波长变化曲线图，图中显示翘曲腹向衰减尺度随翘曲波长的增加呈增加趋势；而相同翘曲波长时，翘曲腹向衰减尺度随边界宽度变化不明显。

图5理想边界腹向衰减尺度曲线变化图

3.2真实边界模型

在真实边界模型中，总应变能随翘曲波长变化如图6所示。可以看出在边界宽度b=0.1 nm时，曲线有明显极值点出现，同样在λ=7附近。而在边界宽度b≥0.2时，总应变能随翘曲波长的增加而呈减小趋势，且无明显极值点出现。相比之下边界宽度b=0.1 nm时总能量最小，石墨烯薄膜整体相对最为稳定。

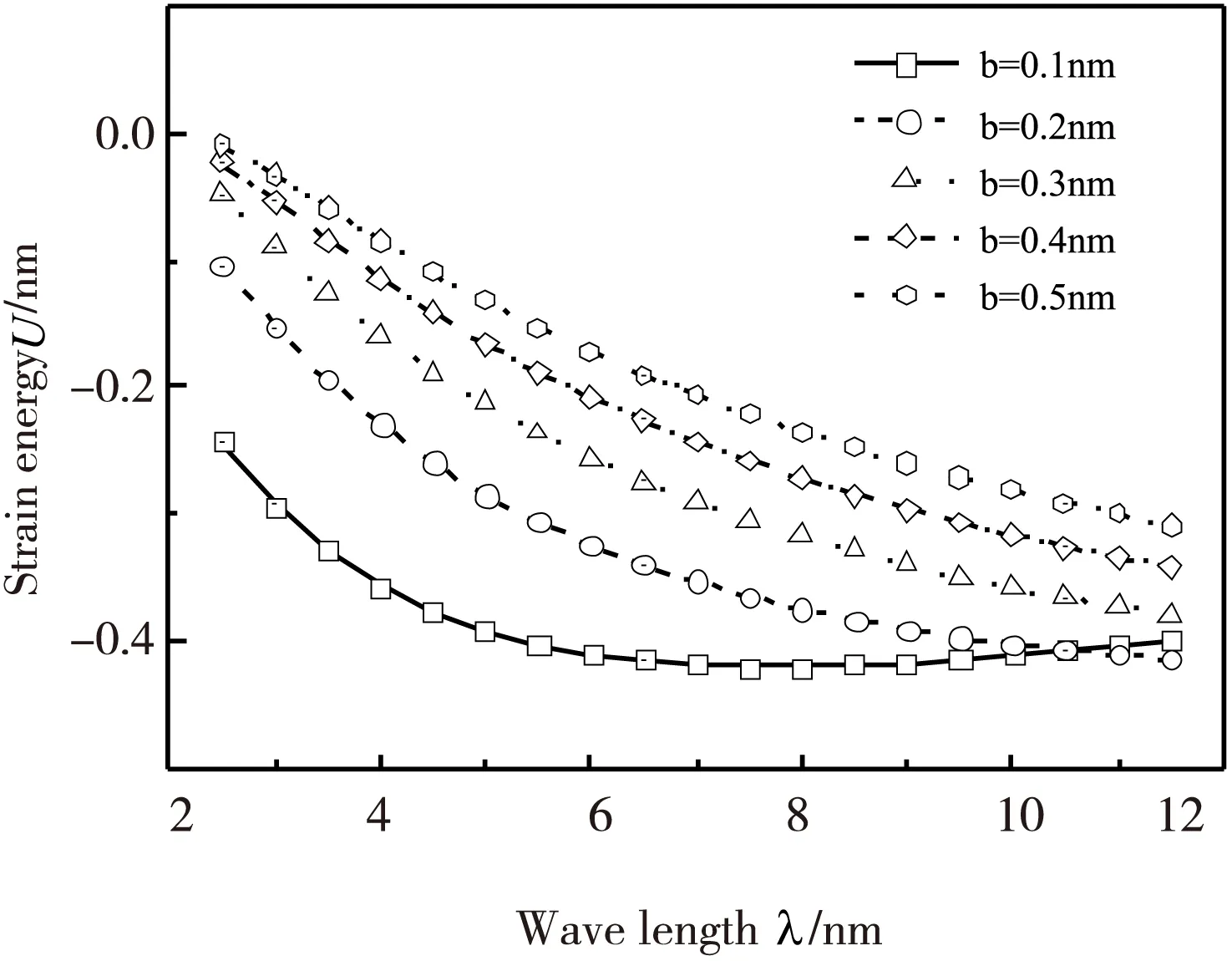
图6真实边界应变能变化曲线图

石墨烯薄膜翘曲幅值随翘曲波长的变化曲线如图7所示，图中显示翘曲幅值随翘曲波长的增加呈增加趋势，且增加速度逐渐减缓；而翘曲波长不变时，翘曲幅值随边界宽度增加而减小。即边界宽度为b=0.1 nm石墨烯薄膜翘曲幅值最大。

图7真实边界翘曲幅值变化曲线图

翘曲腹向衰减尺度随翘曲波长变化曲线如图8所示，从图中容易看出翘曲腹向衰减尺度随翘曲波长的增加呈增加趋势；且翘曲波长不变时，翘曲腹向衰减尺度随边界宽度增加而增加；相比之下，翘曲腹向衰减尺度在b=0.1 nm最小，即对石墨烯薄膜内部影响最弱。

图8真实边界腹向衰减尺度变化曲线图

4　结　论

本文对考虑边界尺寸的石墨烯薄膜由于边界应力发生的翘曲变形进行了理论分析，分别建立了理想边界和真实边界模型，探讨边界宽度的变化对石墨烯薄膜总应变能、翘曲幅值以及翘曲腹向衰减尺度的影响，由数值解得到如下主要结论：

(1) 两种模型均于边界宽度b=0.1 nm时出现总应变能最小值，石墨烯薄膜整体达到相对最稳定变形状态。

(2) 两种模型中翘曲幅值于边界宽度b=0.1 nm时达到最大值。

(3) 理想边界模型翘曲腹向衰减尺度随边界宽度变化可以忽略不计；真实边界模型翘曲腹向衰减尺度b=0.1 nm最小，即对石墨烯薄膜内部影响最弱。

附录A

令

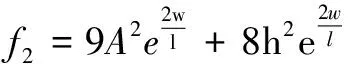
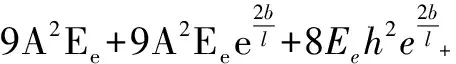
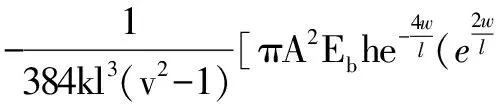
(A1)

(A2)

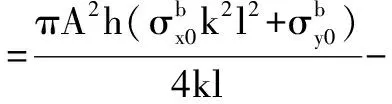
(A3)

(4A)

(A5)

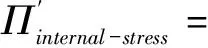
(A6)

[1] NOVOELOV K S,GEIM A K,MOROOV S V,et al.Electric field effect in atomically thin carbon films[J].Science,2004,306(5696):666-669.

[2] BRINK J V D.Gaphene:from strength to strength[J].Nature nanotechnology,2007,2:199-201.

[3] GEIM A K,NOVOSELOV K S.The rise of grahene[J].Nature Materials,2007,6:183-191.

[4] AVOURIS P,CHEN Z,PEREBEINOS V.Caron-based materal[J].Nature Nanotechnology,2007,2:605-615.

[5] LI D,KANER R B.Materials science: graphene-basedmaterials[J].Science,2008,320(5880):1170-1171.

[6] RAO C N,SOOD A K,SUBRAHMANYAM K S,et al.Graphene:the new two-dimensional nanomaterial[J].Anewante Chemie International Edition,2009,48(42):7752-7777.

[7] LEE C,WEI X,KYSAR J W,et al.Measurement of the elastic properties and intrinsic strength of monolayer grapheme[J].Science,2008,321(5887):385-392.

[8] GRATAB R,SHENO V B,RUOFF R S.Anomalous strength characteristics of tilt grain boundaries in graphene[J].Science,2010,330(6006):946-953.

[9] NAIR R R,BLAKE P,GRIGORENKO A N,et al.Fine structure constant defines visual transparency of graphene[J].Science,2008,320(5881):1308.

[10] BUNCH J S,VERBRIDGE S S,ALDEN J S,et al.Impermeable atomic membranes from graphene sheets[J].Nano Letters,2008,8(8):2458-2462.

[11] MOSER J,BARREIRO A.Fine structure constant defines of grapheme[J].Applied Physics Letters,2007,91:1635-1647.

[12] 张芳,史冬梅,暴宁钟,等.石墨烯技术及产业发展现状[J].全球科技经济瞭望,2014(5):45-51.

[13] 胡耀娟,金娟,张卉,等.石墨烯的制备、功能化及在化学中的应用[J].物理化学学报,2010,26(8):2073-2086.

[14] SHENOY V B,REDDY C D,RAMASBRAMANIM A,et al.Edge-stress-induced warping of graphene sheet and nanoribbons[J].Physical Review Letters,2008,101:3382-3390.

[15] REDDY C D,RAMASUBRMANIAM A,SHENOY V B,et al.Edge elastic properties of defect-free single-layer graphene sheets[J].Applied Physics Letters. 2009,94(10):101904-101906.

[16] GOMEZ-NAVARRO C,BURGHRAD M,KERN K.Elastic properties of chemically derived single grapheme sheets[J].Nano Letters,2008,8(7):2045-2049.

[17] POOT M,VAN D Z H S J.Nanomechanical properties of few-layer graphene membranes[J].Applied Physics Letters,2008,92(6):063111-063113.

[18] HUANG Y,WU J,HWANG K C.Thickness of graphene and single-wall carbon nanotubes[J].Physical Review B,2006,74(24):4070-4079.

[19] WU J,PENG J,HWANG K C,et al.The intrinsic stiffness of single-wall carbon nanotubes[J].Mechanics Research Comunications,2008,35(1):2-9.

[20] LU Q,ARROYO M,HUANG R.Elastic bending modulus of monolayer graphene[J].Journal of Physics D:Applied Physics,2009,42(10):102002-102007.

[21] LU Q,HUANG R.Nonlinear mechanics of single-atomic layer graphene sheets[J].International Journal of Applied Mechanics,2009,1(3):443-467.

[22] GUO J G,ZHOU L J,KANG Y L.Chirality-Dependent Anisotropic Elastic Properties of a Monolayer Graphene Nanosheet[J].Journal of Nanoscience & Nanoechnology,2012,12(4):3159-3164.

[23] LEUNG A Y T,GUO X,HE X Q,et al.A continuum model for zigzag single-walled carbon nanotubes[J].Applied Physics Letters,2005,86(8):083110-083112.

[24] GOVINDJEE S,SACKMAN J L.On the use of continuum mechanics to estimate the propertiesof nanotubes[J].Solid State Communication,1990,110:227-230.

[25] GAO X L,LI K.Finite deformation continuum model for single-walled carbon nanotubes[J].International Journal of Solid and Structures,2003,40(26):7329-7337.

Effect of Stress on the Boundary of Graphene Sheets

ZHANGHaizheng,SHIMingxing

(School of Mechanics and Engineering, Southwest Jiaotong University, Chengdu 610031, China)

Theoretical and true edge models are established respectively to study the importance of edge width on edge warping of graphene nanoribbons, which is caused by the edge stress. In both models the graphene nanoribbon itself is treated as an elastic shell. The edge owns a nominal edge area and thus beam model is used for the edge in the theoretical model. In comparison the edge will behave like thin shell as the ribbon itself in the true edge model. The deformation parameters, such as warping period and amplitude and the damping scale inward are analyzed by seeking numerical solutions of a set of nonlinear equations. Theoretical analysis found that, the variation of edge width has significant effects on the three deformation parameters. When the edge width is 0.1nm, total strain can be minimal extremum points about 7 nm wavelength which is consist with the predictions based on molecular dynamics. It is also found that only when the edge width is 0.1nm, edge warping reaches the maximum amplitude and at the same time the warping descends at the rapidest scale inward.

graphene; edge-stress; edge width; edge warping; shell theory

2016-03-30

国家自然科学基金项目(11472229)

张海正(1990-),男,河北唐山人,硕士生,主要从事微纳米结构动力学方面的研究，(E-mail)zhanghaizheng1990@163.com;

师明星(1972-),男,山西朔州人,教授,博士,主要从事柔性电子器件和微纳米材料方面的研究,(E-mail)shimingxing1972@163.com

1673-1549(2016)03-0055-06

10.11863/j.suse.2016.03.12

TN383

A