模拟退火改进蚁群算法的公交网络设计

沈显庆,崔保峰

(黑龙江科技大学 电气与控制工程学院,哈尔滨 150022)



模拟退火改进蚁群算法的公交网络设计

沈显庆,崔保峰

(黑龙江科技大学 电气与控制工程学院,哈尔滨 150022)

针对基本蚁群算法设计公交网络时,出现过早收敛和易陷入局部寻优,导致蚁群搜索停滞的问题，提出一种模拟退火改进蚁群算法。通过总运行时间和乘客总换乘次数构造目标函数，利用模拟退火算法生成比较优秀的初始公交线路集，根据初始线路集初始化信息素，将模拟退火算法的蒙特卡洛循环思想加入蚁群的搜索中，对目标函数进行迭代求解。采用模拟退火算法、基本蚁群算法、改进后的模拟退火蚁群算法对目标函数进行优化对比。结果表明：模拟退火改进蚁群算法比模拟退火算法和蚁群算法的求解效率分别高10.6倍和3.5倍。该算法有效地解决了公交网络设计问题，优化方案可使乘客换乘次数与乘客总乘车时间大幅缩减。

蚁群算法； 模拟退火算法； 公交网络； 目标函数

0　引　言

城市化进程的加快给各大城市交通带来了巨大的压力。面对日益严重的交通拥堵问题，各大城市先后推进“智慧公交”的建设。城市公交网络设计是城市公交规划的基础，合理的公交网络设计直接关系到公众对乘坐公共交通工具出行的热情，其对整个公交网络的运营与调度均至关重要。因此，研究一种能够快速而精确地解决大规模公交网络设计问题的算法具有重要现实意义。

城市公交网络设计现已被证实是一个NP-Hard问题，需要处理的数据量比较大，传统方法很难求其最优解。目前，国内外多采用启发式算法进行优化求解，白子健等[1]提出了一种适用于禁忌搜索算法的优化模型，利用该模型得到了较优解。满英等[2]将模拟退火算法与遗传算法融合，成功地解决了温州滨海新区的规划问题。赵毅等[3]在只考虑公交路线设置的情况下，应用遗传算法对公交线路进行了优化。王佳等[4]采用遗传算法解决了公交网络层次性规划的问题。张辉等[5]采用蜂群算法优化贪婪算法产生的初始线路集得到了较优解。现有研究对公交网络优化问题的求解效率往往不是很高，且对大型公交网络的适用性较差，仍存在很大的提升空间。

笔者根据城市公交网络设计中的关键点，建立以乘客总乘车时间与乘客总换乘次数的加权和为目标函数的模型，通过模拟退火算法生成初始次优路线集，按初始路线集更新初始信息素，利用经过多项改进的蚁群算法优化目标函数，以期能有效地提高问题的解决效率，使改进后蚁群算法能够适用于大规模公交网络优化问题。

1　公交网络模型的建立

笔者研究的城市公交网络设计是在给定公交网络图、乘客需求矩阵(OD矩阵)及公交线路数的情况下，利用改进的模拟退火蚁群算法求解最优路线的问题。

1.1模型假设

(1)公交在线路上运行时不发生意外，且线路畅通。

(2)乘客在所研究时间段内对公交的需求保持不变。

(3)公交在任意线路上的运行时间必须大于规定的最小时间、小于规定的最大时间。

(4)公交运行线路必须覆盖全部站点。

(5)公交任意单条线路不能存在重复站点。

1.2模型的建立

为了将公交网络模型[6-7]设计的较为合理，文中综合考虑了乘客的总乘车时间和乘客的总换乘次数，建立二者的加权和模型：

(1)

式中：F——所建立模型的目标函数，该模型将最优路线问题转化为求取目标函数的最小值问题；

γ1、γ2——乘客总乘车时间和乘客总换乘次数的权值，该权值使二者保持在一个数量级上；

c——总的公交路线数；

S、P——公交起始站点集与公交终点站集；

Qij——站点i到站点j的乘客需求量；

Tkji——第k条线路上公交从站点i到站点j的运行时间；

Zip——如果公交站点i不能直达公交站点p，则Zip=1，否则Zip=0。

模型约束条件考虑到每个站点的平均停留时间t0，每条线路的公交行驶总时间tk不得低于60 min，不得高于90 min。

2　公交网络模型的求解

文中将公交网络设计类比该觅食过程，将起点站类比成蚁群的巢穴，终点站类比成食物源，那么该问题就成了蚁群算法最擅长的问题了。但由于公交网络相当复杂，且存在公交站点全覆盖与单条线路无重复站点等约束条件的限制，使采用基本蚁群算法求解时存在如搜索过早停滞等问题，故笔者提出一些改进，用于解决大型公交网络设计问题。

2.1初始路线集的改进

蚁群算法多采用随机初始化的方式更新初始信息素，由于随机初始化的结果往往都比较差，致使蚁群前期容易陷入无用的搜索。前期信息素的匮乏导致蚁群自身搜索速度较慢，进一步降低了蚁群的搜索速度，因此，在此基础上采用模拟退火算法去生成初始线路集。

模拟退火算法是一种全局搜索算法，它能快速地找到全局次优解，进而可以用此次优解去更新信息素，不但解决了随机初始化时导致容易陷入无用搜索的问题，而且也解决了前期信息素匮乏的问题。具体步骤：

Step1设定初始温度θ、终止温度θ1与退火速度α。为了快速寻找全局次优解，α的值不必太大。随机产生(c-1)条路线，且任意一条路线无重复站点。

Step2产生第c条路线用来补充前(c-1)条路线遗漏的站点，使c条路线覆盖全部站点。当温度下降到终止温度之前继续执行。

Step3设置内部蒙特卡洛循环，随机更换(c-1)条中的k(1≤k≤c-2 )条，补充第c条线路。

Step4计算更新后的线路目标函数值，并计算更新前与更新后的目标函数的差值作为ΔE。如果ΔE≤0,则接受新值；否则如果exp(-ΔE/θ)>rand,则也接受新值，否则舍弃新值。

Step5记录较优秀的路线及目标函数值供下次蒙特卡洛循环使用，直至内部循环结束。

Step6降温T←αT。

2.2改进蚁群算法优化的目标函数

利用模拟退火算法的快速全局寻优产生的次优路线集去更新信息素，但是一个新的问题随之出现，由于信息素的累积速度较快，较优秀的路线被重复叠加信息素的概率较大，而较差的路线上的信息素却在不断挥发而越来越小，致使蚁群的搜索容易出现陷入局部最优甚至搜索停滞等问题。

笔者借鉴最大-最小蚁群系统[8-10](MMAS)的思想，将信息素限制在(τmin,τmax)内，以解决基本蚁群算法求解公交网络设计问题时出现的容易陷入局部最优问题。与传统MMAS的思想不同，文中初始化信息素时仍然按模拟退火算法产生的次优解集去更新信息素轨迹，而不是全部初始化为τmax，当某条路径上的信息素小于τmin时，将该路径上的信息素重新赋值为τmax。

为扩大蚁群搜索范围保证所求结果为全局最优解，在蚁群搜索过程中加入蒙特卡洛循环，该循环通过多次随机更换线路并与之前的线路比较，一方面增加了蚁群搜索的范围，另一方面保留了更优秀的解用来进行信息素的更新。

基本蚁群算法对蚂蚁如何选择下一个路径一般存在两种考虑：一是蚂蚁有50%的概率选择信息素浓度最高的可选路径，有50%的概率按照轮盘赌法选择下一个路径；二是蚂蚁只按轮盘赌法选择下一个路径。针对公交网络设计问题优化了概率选择，使其更适用于大型公交网络的设计。改进的蚁群算法具体实现步骤：

Step1n←0(n为循环次数)，利用模拟退火算法产生的初始次优解按照τnew=ρτold+Q/F更新初始信息素，其中，ρ为信息素持久性系数；τold为信息素初始值，一般设置成相等；Q为信息素总量；F为目标函数值。每次更新完信息素检查各站点信息素量，如果信息素量小于τmin则将其置为τmax。

Step2每只蚂蚁按更新后的信息素去更新路径，选择策略为有35%的概率选择信息素浓度最大的站点，有65%的概率按轮盘赌法选择下一个站点。

Step3设置内层循环，该循环次数较少，但每次循环若产生的路径比step2产生的路径优秀则替换之前的路径，直到循环结束产生更优秀的解。

Step4记录当前最好的路径和目标函数值，n←n+1。

Step5当n大于设定的最大迭代次数时，输出最优解。

3　应用实例

3.1站点需求矩阵

为验证算法的优越性，笔者提供的公交网络图，如图1所示。该公交网络共由25个站点组成，其中包含三个起始站点S={1,2,3}和五个终点站P={21,22,23,24,25},17个中间站点。其中各站点之间的连线表示各站点的可行路径，各站点连线上的数字为公交在站点间的理想行驶时间。

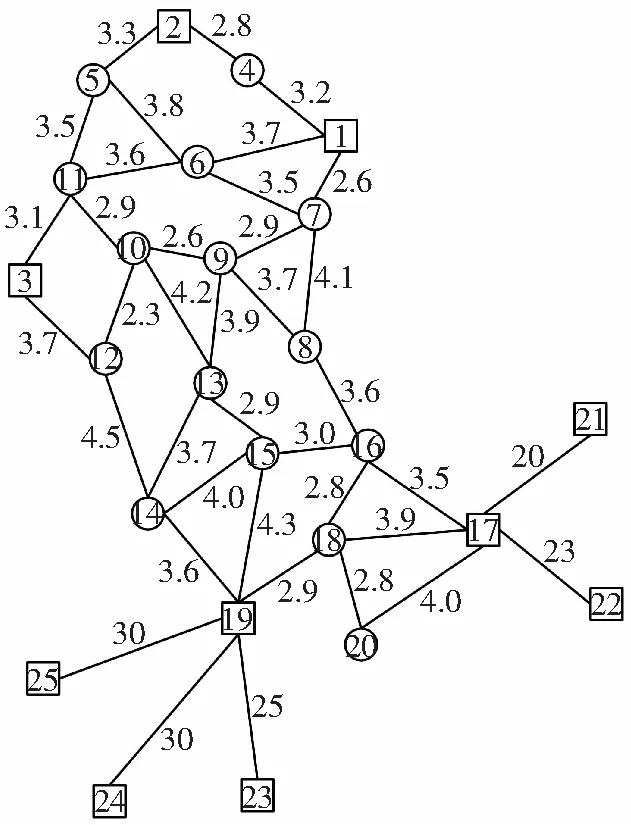
图1　公交网络

公交网络设计中OD需求矩阵也是必需的，表1为图1所对应的站点需求矩阵。

表1　站点需求矩阵

3.2结果与分析

综合考虑OD需求矩阵，取公交总线路数c=6，乘客总乘车时间权重γ1=1.5，乘客总换乘次数权重γ2=2.5，公交平均每站换乘时间t0=1.5，分别用模拟退火算法、基本蚁群算法和改进后的模拟退火蚁群算法优化目标函数，采用Matlab编程，运行环境CPU为英特尔酷睿13处理器、内存4 G。

3.2.1模拟退火算法的求解

经过多次测试，取初始温度θ=20 000 ℃，终止温度θ1=1 ℃，退火速度α=0.95，测试20次得到最优目标函数值曲线，如图2所示。所对应最优线路为{1 6 5 11 10 9 8 16 17 21}、{2 4 1 7 8 16 18 20 17 22}、{3 11 10 9 13 14 15 16 18 19 23}、{2 5 6 11 10 9 8 16 18 19 24}、{3 11 10 9 13 15 19 25}、{3 11 10 12 14 15 19 25}。

图2　模拟退火算法优化过程

Fig.2Optimization process of simulated annealing algorithm

3.2.2基本蚁群算法的求解

初始信息素量Q=200，最大迭代次数nmax=30(测试时发现当nmax>30时，蚁群搜索缓慢，并且易出现停滞状态)，信息素持久系数ρ=0.85。测试20次得到最优目标函数值曲线,如图3所示。所对应最优线路为{1 6 7 9 13 14 19 18 17 21}、{2 4 1 6 7 8 16 18 17 22}、{3 12 10 9 13 14 15 19 23}、{2 5 6 7 9 13 14 19 24}、{2 5 6 7 9 13 14 19 25}、{3 11 6 7 8 16 18 20 17 22}。

图3　基本蚁群算法优化过程

Fig.3Optimization process of basic ant colony algorithm

3.2.3模拟退火改进蚁群算法的求解

初始温度θ=20 000 ℃，终止温度θ1=1 ℃，退火速度α=0.6，初始信息素量Q=200，最大迭代次数nmax=50，信息素持久系数ρ=0.85，τmin=0.05，τmin=0.1，测试20次得到最优目标函数值曲线，如图4所示。所对应最优线路为{3 11 6 7 8 16 18 20 17 21}、{3 12 14 13 9 8 16 17 22}、{1 6 11 10 13 15 14 19 23}、{2 5 6 11 10 13 14 19 24}、{3 11 5 6 1 7 8 16 18 19 25}、{2 4 1 6 11 10 13 14 19 24}。

图4　模拟退火改进的蚁群算法优化过程

Fig.4Optimization process of simulated annealing improved ant colony algorithm

3.3算法对比

笔者分别采用模拟退火算法、基本蚁群算法和模拟退火改进的蚁群算法对目标函数进行了20次优化，设平均求解时间为t，对比结果，如表2所示。

表2　不同算法结果对比

从表2可以看出，模拟退火改进的蚁群算法比基本蚁群算法和模拟退火算法在解决公交网络设计时更优秀，具有求解速度快、优化结果更加精确的特点。

4　结　论

(1)该研究考虑乘客总乘车时间与乘客总换乘次数,结合OD矩阵建立了公交网络的模型，通过模拟退火算法产生初始次优公交路线集，利用改进的蚁群算法对初始次优路线集迭代寻优，优化目标函数最终得到最优的公交线路集。

(2)与既有研究对比，模拟退火改进的蚁群算法有效地解决了公交网络设计，优化方案可使乘客换乘次数与乘客总乘车时间大幅缩减，具有很好的适用性。

(3)模拟退火改进的蚁群算法在解决公交网络设计问题时能找到三种算法的最优解，最差解与平均解，均优于基本蚁群和模拟退火算法的解，求解效率是模拟退火算法的10.6倍，是基本蚁群算法的3.5倍。

[1]白子健,赵淑芝,田振中.公共交通网络优化的禁忌算法设计与实现[J].吉林大学学报:工学版,2006,36(3):340-344.

[2]满英,刘三阳,陈小娟.基于改进的模拟退火遗传算法的公交线网优化[J].四川理工学院学报:自然科学版,2008,21(1):1-3.

[3]赵毅,钟声.基于遗传算法的城市公交路线优化问题[J].计算机工程与科学,2012,34(9):109-112.

[4]王佳,符卓,杜靖毅.基于遗传算法的城市公交骨架线网优化设计[J].计算机应用研究,2012,29(12):4518-4533.

[5]张辉,赵鹏.基于改进蜂群算法的城市公交网络设计[J].北京交通大学学报,2015,39(4):118-124.

[6]金孟合,王慧.基于蚁群算法的公交路线走向模型及其求解[J].江南大学学报:自然科学版,2007,6(2):239-242.

[7]张莉,沈文国,安新磊.一种新的多重权重复杂公交网络模型的研究[J].武汉理工大学学报:交通科学与工程版,2016,40(1):105-109.

[8]姚艳.一种最大最小蚂蚁系统的改进算法[J].数学的实践与认识,2014,44(5):242-247.

[9]高维,景小荣.基于MMAS的MIMO_OFDM系统上行多用户检测[J].重庆邮电大学学报：自然科学版,2015,27(6):745-749.

[10]王晶,王雪峰,王肖杰,等.基于改进型MMAS算法的微电源容量优化布址[J].电力系统自动化,2015,39(2):73-80.

(编辑李德根)

Transit network design based on simulated annealing improved ant colony algorithm

SHEN Xianqing,CUI Baofeng

(School of Electrical &Control Engineering,Heilongjiang University of Science &Technology,Harbin 150022,China)

This paper proposes an improved ant colony algorithm based on simulated annealing as an alternative to the basic ant colony algorithm plagued by such drawbacks as premature convergence and vunerability to the local optimization with a resulting stagnation in ant colony search,such as is the case with the basic ant colony algorithm.This algorithm works firstly by constructing the objective function by the total running time and the total number of passengers transfer;then by generating a better initial bus line set using the simulated annealing algorithm;and ultimately by drawing on the initial line set initialization pheromone and applying the Monte Carlo cycle of simulated annealing algorithm to the ant colony search and thereby solving the objective function through loop iteration.The algorithm is validated by optimization and comparison of objective function using the simulated annealing algorithm,basic ant colony algorithm,and the improved ant colony algorithm and simulated annealing.Results show that the improved ant colony algorithm boasts 10.6 and 3.5 times respectively higher than efficiency the simulated annealing algorithm and the ant colony algorithm.The algorithm may provide an effective solution to the bus network design,and the resulting optimization scheme may afford a significant reduction in the passenger transfer times and the total passenger travel time.

ant colony algorithm;simulated annealing;transit network;objective function

2016-04-06

沈显庆(1969-),男，吉林省通化人，教授，博士，研究方向：伺服系统与智能控制，E-mail:shenxianqing2001@163.com。

10.3969/j.issn.2095-7262.2016.03.019

TP301.6； U491.12

2095-7262(2016)03-0327-05

A