利用组合型交叉熵实现多处理机调度的算法

车向前，张欣欣，边　莉

(1.黑龙江科技大学 计算机与信息工程学院，哈尔滨 150022； 2.黑龙江科技大学 电气与控制工程学院， 哈尔滨 150022； 3.黑龙江科技大学 电子与信息工程学院，哈尔滨 150022)



利用组合型交叉熵实现多处理机调度的算法

车向前1，张欣欣2，边莉3

(1.黑龙江科技大学 计算机与信息工程学院，哈尔滨 150022； 2.黑龙江科技大学 电气与控制工程学院， 哈尔滨 150022； 3.黑龙江科技大学 电子与信息工程学院，哈尔滨 150022)

为提高大型多处理机调度的效率与稳定性，提出一种利用组合型交叉熵实现多处理机调度的方法。该方法依据处理机与作业的约束关系，将处理机调度问题表示为使目标函数最小化的线性0-1整数规划模型，采用组合型交叉熵算法对该模型进行优化求解。利用组合型交叉熵算法对多处理机问题的具体事例进行测试，与模拟退火算法和蚁群算法的测试结果对比分析。结果表明：组合交叉熵算法的优化速度是蚁群算法的6.1倍，是模拟退火的29.5倍，该算法稳定性高，收敛速度快，运行时间短，在解决大型多处理机问题时效率明显高于模拟退火算法和蚁群算法。

组合型交叉熵； 多处理机调度； 0-1整数规划

0　引　言

并行分布式计算是当前科学领域研究的热点问题。并行算法的设计、任务的划分、通信的协调和同步、多任务的调度是目前并行分布式计算需要解决的问题，其中任务的调度会直接影响计算的效率，因此，如何合理高效地进行多任务的调度与分配是目前亟须解决的难题。多处理机调度问题[1-3]的应用及理论方面的研究，得到了科学领域研究者的极大关注。多处理机调度问题实质是NP完全问题，传统的线性规划无法解决，目前，国内外多采用启发式算法近似求解。文献[4]利用蚁群算法实现多处理机调度问题，每个处理机对应一只蚂蚁，每次迭代过程中并行蚂蚁由主控进程生成，当所有蚂蚁完成一次搜索时再进行同步，这种方法增加了执行时间。文献[5]采用动态信息素更新和参数选择，将蚁群算法进行改进，该方法在保证收敛速度的条件下能够得到全局最优解，很好地解决了多处理机任务调度问题。但这种方法存在收敛速度慢、效率较低等不足。文献[6]将量子计算和粒子群算法结合解决多处理机调度问题，虽然操作简单，容易实现，但是效率低、易陷入局部最优解。针对现有研究解决多处理机问题时普遍存在收敛速度较慢、效率较低的现状，笔者引入了组合型交叉熵算法。

1　多处理机调度模型

多处理机调度问题是指有c台型号相同的处理机H1，H2，…，Hc，d项相互独立的作业T1，T2，…，Td，作业独立工作，而且每项作业在每台处理机上工作的概率相同，但是每项作业不允许中断。d项相互独立的作业不能拆分为更小的子作业。调度的目的是给出一种合理优越的调度方案，使c台处理机以尽量短的时间完成d项作业[7]。多处理机调度问题的目标是指在满足一定性能指标和约束条件的前提下，将可并行的任务按适当的分配策略确定一种分派和执行顺序，合理分配到各处理机上有序执行，以达到减少总执行时间的目标。因此，多处理机调度问题的数学模型如式(1)所示。多处理机调度问题的目的即求z的最小值。

(1)

式中:z——完成d项作业所需要的时间；

ynm=1——作业Tm在处理机Hn上处理；

tm——处理机完成作业Tm的时间；

根据多处理机调度问题的特点和模型可知，多处理机调度问题属于离散优化问题，文中应用CE对多处理机问题进行优化求解，即通过交叉熵算法求出z的最小值。因为ynm的取值为0或1，所以多处理机调度问题是0-1整数规划问题。

2　交叉熵算法

交叉熵算法[8](Cross entropy algorithm，CE)是以信息论中的交叉熵理论为基础提出的一种全局随机优化算法。近些年来,交叉熵算法被应用到故障诊断、预测等大型复杂、优化问题中。该算法的基本特征是在优化过程中根据参数化概率密度分布，使每次迭代使用的候选样本都发生变化。因此，CE算法优化过程中的关键是迭代，具体的实现过程可分为两步[9-12]：一是由给定的概率密度函数生成一组随机样本；二是根据产生的随机样本更新概率密度函数，进而为下一步迭代产生更优的样本数据。

2.1交叉熵算法的基本原理

针对优化问题

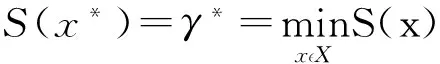
(2)

式中：S——X上的实值函数；

x*——所求问题的最优解；

γ*——所求函数S的最小值。

CE算法将以上优化问题转化为概率问题，即转化为求S(X)比已知参数γ小的概率问题。该问题可表示为

l(γ)=Pv(S(X)≤γ)=

(3)

式中：X=(x1,x2,…，xn)随机向量，由f(·，v)产生的随机样本；

f(·,u)——概率密度函数；

I{S(X)≤γ}——指示函数；

γ——给定实数；

l——S(X)比给定实数γ小的概率；

I{S(X)≤γ}——指示函数集合；

Ev——相应的期望值。

当γ接近γ*时，l值将会越来越小，因此，为了有意义，值不能太小，则γ和v的选取至关重要。为了解决此问题，采用多级别算法，构造分布参数序列{vt，t>0}和级别序列{γt，t>0}，t为迭代次数。将vt和γt进行更新迭代，一直到某次迭代后分布参数序列中对应元素改变量的最大值小于某一规定的参数btol，则迭代结束[13]。

2.2组合型交叉熵算法

CE算法分为连续型交叉熵算法和组合型交叉熵算法[14]，组合型交叉熵算法(CCE)是用来处理离散型数据，而连续性交叉熵算法是用来处理连续性数据。两者之间的区别在于概率密度函数的选择，针对组合优化问题组合型交叉熵算法的概率密度函数为Berboulli分布。设成功概率为p，则CCE算法的概率密度函数为

f(x;p)=px(1-p)1-x，

(4)

式中,当x=1时，f(x；p)=p；

当x=0时，f(x;p)=1-p。

CCE算法的步骤为：

第一步设置初始值P(0)(n为P(0)的维数)，最佳样本的分数ρ，样本数M，平滑系数α，迭代次数t=0，终止参数btol。

第二步令t=t+1，Pt-1以Bernoulli分布产生M+n的样本矩阵Xt=(X1(t),X2(t),…,XM(t))，其中Xm(t)=(xm(t),1,xm(t),2,…，xm(t),n)，1≤m≤M 。

γ(t)=S[(1-ρ)M]。

(5)

第四步利用式(6)更新参数P：

(6)

第五步利用平滑参数α，对pj处理，如式(7)所示：

pj=αpj+(1-α)pj-1。

(7)

第六步若相邻两次迭代产生的参数矩阵满足式(8),则停止迭代，否则从第二步开始重新迭代。

(8)

3　算　例

文献[8]中的实例，三台相同的处理机和九项作业，为了验证算法在解决大型多处理机调度问题时的有效性与优越性，现取d=21项作业，算法复杂度以指数剧增。每项作业需要运行的时间tm=(81,40,26,4,65,98,53,71,15,23,45,78,56,12,31,28,60,21,17,32,35)，下面解决如何使21项作业在尽可能短的时间内由三台处理机完成的NP完全问题。设Ynm为作业Tm分配到处理机Hn上所有的处理方案，则多处理机调度问题的求解由式(1)转化式(9)

(9)

3.1多处理机调度问题的CCE算法

根据多处理机调度问题的数学模型可得,CCE算法的目标函数式(9)为z，z中的变量ynm的取值为0和1，ynm服从Bernoulli分布，因此，该算法可以解决多处理机调度问题。为了得到目标函数的最小值，利用CCE算法优化目标函数z，选取初始为P0=(0.5，0.5，…，0.5)(P0的维数为n)，ρ=0.85，M=60，α=0.9，btol=0.1× 10-3。文中的实验环境为CPU 1.8 GHz，内存为4 G，采用Matlab对该问题编程，程序运行10次，结果见表1。

表1　CCE算法的10次运行结果

由表1可知，计算结果平均在第11次收敛，选取10次计算结果中最好解，目标函数与迭代次数nd的关系，如图1所示。

图1　CCE算法的计算过程

由图1可见，CCE算法在第13次迭代时已经寻找到了种群最优适应值，z=286。对应的调度方案为H1(81,26,98,28,21,32)，H2(15,45,78,56,31,60),H3(40,4,65,53,71,23,12,17,35)，调度时间为286 s。

3.2三种算法的比较

针对多处理机调度问题，采用模拟退火算法和蚁群算法与CCE算法进行对比分析。经过实验分析与验证，模拟退火算法中起始温度20 000 ℃，终止温度1 ℃，退火速度α=0.97。相同条件下测试10次最好解的测试结果，如图2所示。蚁群算法中信息素持久性系数ρ=0.8，信息素总量Q=200，相同条件下测试10次最好解的测试结果，如图3所示。

图2　模拟退火算法的计算过程

Fig.2Calculation process of simulated annealing algorithm

图3　蚁群算法的计算过程

表2　三种算法结果比较

综合三种算法对多处理机调度问题的测试结果，CCE算法比模拟退火算法和蚁群算法具有运行时间短、收敛速度快、稳定性高的优势，可以在大型多处理机调度方案中应用。

4　结　论

(1)将组合型交叉熵算法应用到多处理机调度问题中，通过对该算法和多处理机调度问题的建模和仿真分析，得出CCE算法的优化速度是蚁群算法的6.1倍，是模拟退火算法的29.5倍。

(2)CCE算法的平均值为293.1，小于蚁群算法和模拟退火算法，说明CCE算法稳定性更高。将CCE算法应用于更大的多处理机调度问题，该算法调度任务时会节省很多时间。

(3)CCE算法可解决多处理机调度问题，证明该算法具有稳定性高、收敛速度快、运行时间短等优势。

(4)文中对于可转化为类似多处理机问题模型的解决方案，提供了一种全新的思路，交叉熵算法可以应用到众多工程问题的解决方案中。

[1]曹杰先,秦永彬,许道云.求解多处理机调度问题的近似算法[J].计算机工程与设计,2014,35(7):2407-2411.

[2]MU PENGCHENG,NEZAN JEANFRAN.Advanced list scheduling heuristic for task scheduling with communication contention for parallel embedded systems [J].Science China Information Sciences,2010,53(11):2272-2286.

[3]DA LI,LEI ZHANG.An efficient dynamic scheduling for multiprocessor architecture[J].International Conference on Electrical and Computer Engineering,2012,12(1):125-130.

[4]郭乘涛,江志斌.应用混合蚁群算法求解并行批处理机组批与调度问题[J].上海交通大学学报,2010,44(8):1068-1073.[5]邓酩,谢晓兰,程小辉.多处理机调度问题的蚁群优化算法[J].桂林理工大学学报,2013,33(2):329-332.

[6]黄天赦,叶春明,叶伟.关于多处理机调度问题的量子粒子群算法研究[J].计算机工程与应用,2009,45(9):49-51.

[7]高尚,杨静宇.群智能算法及其应用[M].北京:中国水利水电出版社,2006:24-28.

[8]REUVEN Y RUBINSTEIN.The Cross-entropy method:a unified approach to combinatorial optimization[M].Australia:Springer-Verlag New York Inc,2004:15-25.

[9]边莉,车向前,张少卿.基于改进交叉熵算法多目标不等间距阵列综合[J].上海交通大学学报,2014,48(3):372-376.

[10]MINVIELLE P,TANTAR E.Sparse antenna array optimization with the cross-entropy method[J].IEEE Transaction on Antennas and Propagation,2011,59(8)：2862-2871.

[11]WANG CHUANSHENG,QIU YUE.Vehicle routing problem with stochastic demandsand simultaneous delivery and pickup based on the cross-entropy method[J].Advances in Automation and Robotics,2012,10(2):55-60.

[12]陈宁,沙倩,汤奕.基于交叉熵理论的风电功率组合预测方法[J].中国电机工程学报,2012,32(4):29-34.

[13]边莉,边晨源.基于组合型交叉熵算法的多电源配电网故障定位[J].电力科学与技术学报,2014,29 (3):86-91.

[14]边莉,边晨源.组合型交叉熵算法在电网故障诊断中的应用[J].电力系统及其自动化学报,2015,27 (10):41-47.

(编辑李德根)

Problem of multiprocessor scheduling based on combinatorial cross-entropy algorithm

CHE Xiangqian1,ZHANG Xinxin2,BIAN Li3

(1.School of Computer &Information Engineering,Heilongjiang University of Science &Technology,Harbin 150022,China； 2.School of Electrical &Control Engineering,Heilongjiang University of Science &Technology,Harbin 150022,China； 3.School of Electronic &Information Engineering,Heilongjiang University of Science &Technology,Harbin 150022,China)

This paper presents a novel method designed for realizing multiprocessor scheduling using combinatorial cross entropy as part of the dedicated efforts to improve the efficiency and stability of a large multiprocessor scheduling.This method works by using the constraint relation between processor and job to define the multiprocessor scheduling as a 0-1 integer programming model for minimizing the objective function;realizing the optimal solution using the combinatorial cross-entropy algorithm;testing the concrete example of the multiprocessor scheduling problem using the combinatorial cross-entropy algorithm;and performing a comparative analysis of the results with the simulated annealing algorithm and the ant colony algorithm.Results demonstrate that the combinatorial cross entropy algorithm working at 6.1 times and 29.5 times respectively the speed of the ant colony algorithm and simulated annealing boasts a significantly greater efficiency than simulated annealing algorithm and ant colony algorithm in solving the large scale multiprocessor scheduling problem.

combinatorial cross-entropy algorithm;multiprocessor scheduling problem;0-1 integer programming problem

2016-02-01

国家自然科学基金项目(51504085)

车向前(1978-)，男，黑龙江省克东人，副教授，硕士，研究方向：图像处理、机器视觉、逆向工程，E-mail:che_xq@163.com。

10.3969/j.issn.2095-7262.2016.03.018

TP301.6

2095-7262(2016)03-0323-04

A