OFDM水声通信多普勒频移的最大似然估计

郭铁梁，任敦亮，郝俊才，姜洪喜

(黑龙江科技大学 理学院，哈尔滨 150022)



OFDM水声通信多普勒频移的最大似然估计

郭铁梁，任敦亮，郝俊才，姜洪喜

(黑龙江科技大学 理学院，哈尔滨 150022)

针对水声信道的时间、空间及频率变化特性，以及由于发射机和接收机之间相对运动产生的多普勒频移对OFDM子载波间正交性的破坏问题，提出一种OFDM水声通信系统多普勒频移的估计方法，用于估计和补偿接收机的多普勒频移。该方法以OFDM数据块为研究对象，假设在一个OFDM数据块内多普勒因子不随路径变化，采用最大似然估计算法估计多普勒频移，通过仿真分析系统多普勒因子临界值，并将多普勒因子估计方差与克拉美罗界进行比较。结果表明：系统存在一个信噪比范围并-15～0 dB，此时估计方差最接近于克拉美罗界。该方法还可以给出系统多普勒因子的临界值，能够保证在不同信道条件下估计参数的一致性，提高了多普勒因子的估计精度。

水声通信； 正交频分复用； 多普勒频移； 最大似然估计； 克拉美罗界

0　引　言

正交频分复用(Orthogonal frequency division multiplexing,OFDM)技术能够很好地解决由多径效应而引起的频率选择性衰落问题，因此，在水声无线通信领域已广泛应用。水声信道存在时空频变特性，加之发射机和接收机存在相对运动，由此产生了多普勒频移。这种频移影响载波跟踪和信号同步，也破坏OFDM子载波间的正交性。

对于OFDM水声通信系统多普勒频移估计问题，近年来，研究者提出多种解决方法。早期的研究是通过在OFDM信号中添加训练序列或导频对多普勒频移进行估计[1-3]。Shaif等[4]提出在数据块首尾添加一对已知波形的线性调频(Linear frequency modulation,LFM)信号，然后在接收端利用相关器检测数据块前后的LFM信号，通过测量上述两个LFM信号之间的数据块在时间上的伸缩变化来估计多普勒因子。计算出多普勒因子之后，通过对该数据块进行采样率转换就可以补偿多普勒频移，传输距离为100～3 000 m，误码率为4×10-3。此后,Beaujean等[5]又进行了改进，这种方法简单适用，得到了广泛的应用。但上述方法的应用是有前提条件的，即假设在一个数据块持续时间内收发双方的多普勒频移不变。由于这种方法是将整个数据块缓存后进行相应地计算与处理，如果在接收的过程中收发双方的相对速度发生了改变，这种方法将引起较大的误差。

S.Mason等[6]提出了利用一系列并行自相关器对数据块的同步信号进行相关运算来估算多普勒因子的方法。张翔采[7]用模糊函数法处理多普勒问题也属于上述方法。这类方法不需要缓存整个数据块就能够进行相应的处理与运算，且可以控制系统的估计精度。这样接收端就可以根据不同情况进行相应的系统设置。这种方法的缺点是硬件数量及计算复杂度很高。

崔健等[8]提出了几种处理OFDM水声通信系统多普勒频移的方法。其中一种方法是采用循环前缀相关估计多普勒因子，并利用线性插值重采样的方法进行多普勒校正。文献[8]还综合利用循环前缀和训练序列进行多普勒估计与补偿。另外，常娟等[9]提出利用功率谱的分布对最大多普勒频移进行估计。这种方法复杂度低、精度较高，但该算法在多径的情况下效果不理想。M.Stojanovic等[10]将水声信道的多普勒频移估计和补偿分两步，分别是宽带补偿和窄带补偿[10]，2013年，M.Stojanovic在文献[2]中又采用了多倍重采样技术对多普勒频移进行补偿。而文献[11]采用中继前向放大与重采样技术相结合的方法估计和补偿多普勒频移。陈阳等[12]通过水上实验对两种OFDM系统多普勒频偏估计算法进行了对比，其中基于拷贝相关时延差估计的多普勒估计算法结构简单、易于实现，而基于空载波的算法较复杂，但精度较高。徐小卡[13]提出了在频域测量多普勒展缩因子的算法，即在发射端发送频率已知的单频信号，然后在接收端对该信号进行测频，这样通过频率的变化就可获得多普勒因子，再利用循环前缀估计窄带多普勒频移。文献[14]主要采用了基于过采样与线性插值的宽带多普勒频移估计与补偿，然后再采用基于多普勒因子候选值与空载波能量相结合的窄带多普勒频移估计。

上述文献中多种多普勒频移的估计方法在算法的精度、运算量或硬件设备的复杂度等几个方面各有优缺点，但并没有讨论算法在不同系统中的一致性问题，即同一方法对系统不同条件下的适应性问题。笔者综合考虑上述问题，提出一种OFDM水声通信系统接收机多普勒频的最大似然估计方法，给出了这种估计方法的克拉美罗界(Cramer rao bound,CRB)。

1　信号与系统模型

1.1OFDM的数学描述

如果一组二进制数据在发射端被传送，首先将该组数据映射成为N个复数序列{d[0]，d[1]，…,d[N-1]}，再对这一复数序列做逆离散傅里叶变换(Inverse discrete fourier transform,IDFT)，则得到N个新复数序列{s[0]，s[1]，…,s[N-1]}，其中,

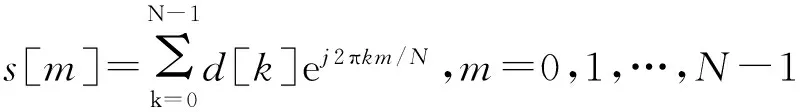
(1)

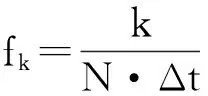
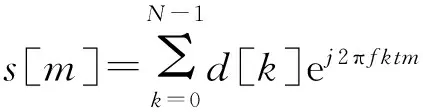
(2)

因此，式(2)表示的是一个多个载波调制信号的和。其相邻子载波间的频率之差为

Δf=fk-fk-1=1/N·Δt=1/T。

如果以Δt的时间间隔把序列{s[0]，s[1]，…,s[N-1]}进行数模转换，滤波输出后得到的连续信号形式：

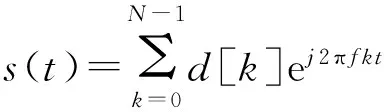
(3)

在接收端，对式(3)接收到的连续信号，以Δt为时间间隔进行采样，然后进行离散傅里叶变换(Discrete fourier transform,DFT)，则复数序列{d[0]，d[1]，…,d[N-1]}可以得到恢复，进而通过与接收端相反的映射关系恢复出二进制数据。为减少计算量，提高系统效率，通常采用快速傅里叶变换算法代替离散傅里叶变换进行计算。

1.2OFDM水声通信系统的多普勒频移

一般情况下，多普勒频移Δfd由声速、收发设备之间的相对速度以及信号传输方向和径向速度之间的夹角所决定。如图1所示，A为发射机，C为接收机，当发射机相对于接收机以速度v从A点向B点方向移动时(B表示v的方向)，Δfd的计算：

Δfd=(v/c)·f·cosφ，

(4)

式中：v——发送设备相对于参照物的运动速度，m/s；

c——水中声波的传播速度，m/s；

f——信号的传输频率，Hz；

φ——AC与AB的夹角，rad。

最简单的情况是φ=0，再令a=v/c，则式(4)变为

Δfd=a·f，

(5)

式中:Δfd——多普勒频移；

a——多普勒因子。

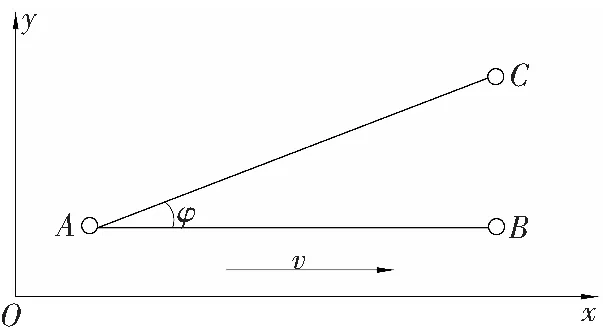
图1　发射机与接收机之间相对运动引起的多普勒频移

Fig.1Doppler shift caused by relative motion between transmitter and receiver

用T表示OFDM符号的周期(无保护间隔)，各子载波频率间隔Δf=1/T，设子载波数量为N，则第k个子载波的频率表示为

fk=fc+kΔf,k=0,1,…,N-1，

式中：fc——中心载波频率。

在一个OFDM符号周期T内，第k个子载波上所传送的复数信息符号用d[k]表示，则系统所传送的带通信号：

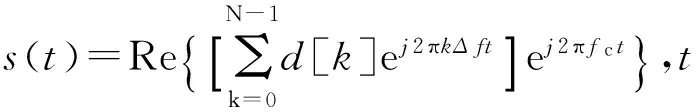
(6)

由于水声信道的多径效应，其冲激响应表示为

(7)

式中：p——多径数；

Ap(t)——第p个路径信号的幅值；

δ(t)——单位冲激信号；

τp(t)——第p个路径的时延。

为简化研究过程，假设各路径具有相同的幅值Ap和相同的多普勒因子a，则有：

(8)

再设在一个OFDM符号周期T内，式(8)中Ap、τp和a均为常数，则系统接收到的带通信号：

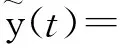
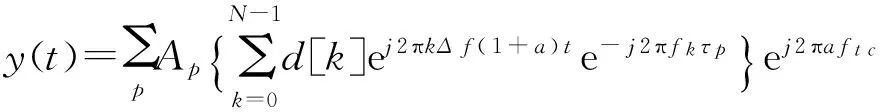
(9)

式中:n(t)——基带信号中的加性高斯噪声。

式(9)中存在两处频率偏移[10]：

(1) 宽带多普勒频移。OFDM符号周期由T变为T/(1+a)。这时每一子载波都发生了与该子载波频率和a有关的多普勒频移ej2πkaΔft。

(2) 窄带多普勒频移。所有子载波共同产生了一个与中心载波和a有关的多普勒频移ej2πafct。

在实际的水声通信系统中，当水下声速为c=1 500 m/s，并且发射机和接收机的最大相对运动速度为vmax=6 m/s时，产生的多普勒因子为amax=1±0.004。而对于陆上无线电磁通信，当电磁波速为c=3×108m/s,vmax=60 m/s，时，amax=1±2×10-7。针对上述数据，对于一个1 024点的OFDM符号，水声信道大约产生一个四倍采样周期的时延，而对于陆上无线电磁通信，则仅产生一个2×10-4倍采样周期的时延。由此可见，多普勒频移对于OFDM水声通信系统所产生的严重影响。因此，在接收端对OFDM符号解调之前，必须对多普勒效应所产生的信号展缩与载波频移进行估计，然后加以补偿与校正，否则就会产生严重的子载波间干扰和误码率。

多普勒效应在时域上表现为接收信号的压缩或伸展，这种影响通常表示为

y(t)=s[(1+a)t]，

(10)

式中：s(t)——发射信号；

y(t)——具有多普勒频移的接收信号。

式(10)表示的是模拟信号，y(t)在接收端被采样后可写成离散时间信号形式：

y[m]=s[(1+a)m]，

式中：m——整数。

在已知多普勒因子a的条件下，对接收信号y[m]进行重采样，就可以在接收端恢复原信号：

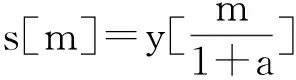
(11)

如果将式(9)写成离散时间信号形式，设奈奎斯特采样周期为T/N，可得：

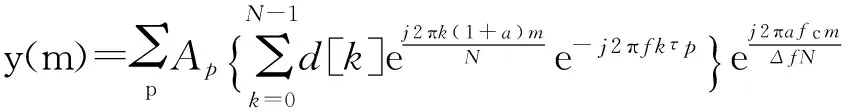
(12)

由式(11)，对式(12)进行采样率转换，略去噪声项，得：

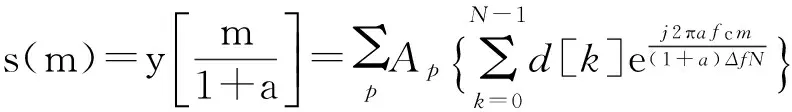
(13)

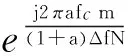
只有再进一步消除窄带多普勒频偏对接收信号的影响，OFDM信号才能顺利通过DFT进行解调。因此，接收端对基带信号s(m)进行宽带多普勒频移补偿之后，还必须进行CFO补偿：

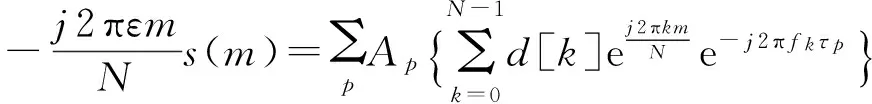
(14)

经式(13)和式(14)的补偿算法之后，就可大幅减小多普勒效应对OFDM水声通信系统所产生的影响，降低由此而引起的子载波间干扰，以恢复子载波间的正交性，进而能够顺利进行DFT运算。因此可知，多普勒因子a的估计算法或方法是解决多普勒频移的一个关键问题。

2　最大似然估计与克拉美罗界

2.1多普勒因子a的最大似然估计

为了突出研究问题的重点，需做一些必要的简化工作。对于式(12)，只保留一条路径，在理想均衡与同步的前提下，只存在噪声和多普勒效应对接收信号的影响。式(12)简化为

y(m)=x[m](a)+n[m]，

(15)

其中,

考虑到接收端由于多普勒效应使信号发生展缩，对整数m的取值范围加以修正。设m的范围为，0≤m≤M-1，M应根据保护间隔的长度加以确定。

下面定义三个矩阵：

Y=[y[0]，y[1]，…，y[M-1]]T,

X(a)=[x[0](a)，x[1](a)，…，x[M-1](a)]T,

N=[n[0]，n[1]，…，n[M-1]]T,

式中：Y——接收到的总信号；

X(a)——接收信号中受到多普勒效应影响的有效成分；

N——接收信号中均值为0，方差为σ2的噪声。

根据式(15)，可得到上述三个矩阵关系：

Y=X(a)+N。

为了应用最大似然方法对多普勒因子a进行估计，应将X(0)作为已知条件，可以认为接收机已知某一OFDM数据块的全部信息，对于这一数据块相当于没有多普勒效应的影响，或者说a=0。下面就利用接收机接收到的这一数据块的实际数据Y以及X(0)，对多普勒因子a进行最大似然估计。基于上述假设，有：

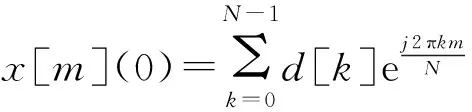
故

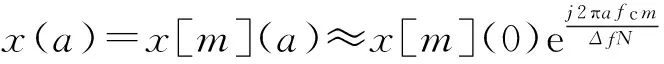
(16)

下面构造似然函数，概率密度函数为

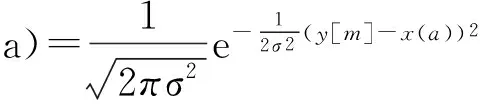
式中：0≤m≤M-1。

最大似然函数为

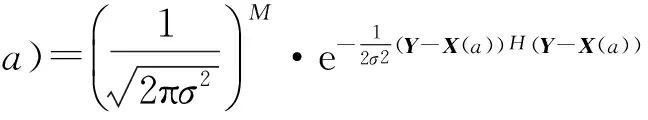
对上述似然函数取自然对数:

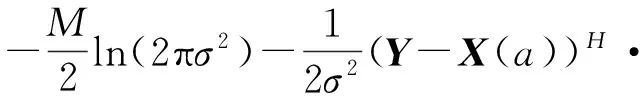
(17)

将式(17)对a取一阶导数：

X(a)HX(a)]

(18)

式(18)中，YHY表示OFDM数据块的能量。当子载波数量足够大时，这一数值近似为常数，所以其导数为0，这样式(18)可以近似表示：

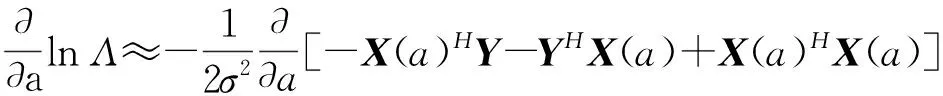
(19)

最后，根据相应的求极值的算法，即可求出多普勒因子的最大似然估计值:

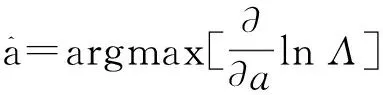
2.2克拉美罗界

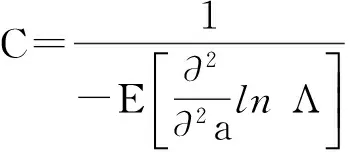
(20)

对式(19)进行展开计算：

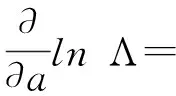
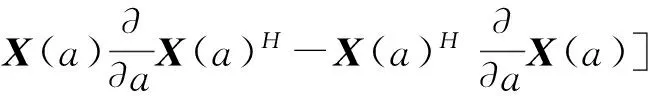
(21)

然后式(21)两边对a再求一次导数：

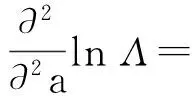
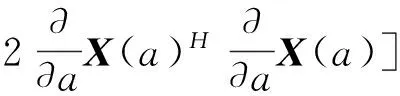
又由于

E[(Y-X(a))]=E[(Y-X(a))H]=E[N]=0，

所以式(20)变换为

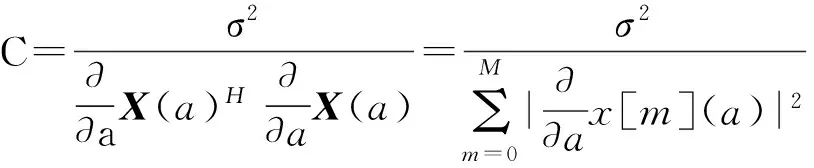
根据式(16)，

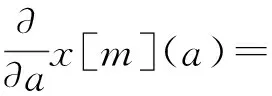
所以

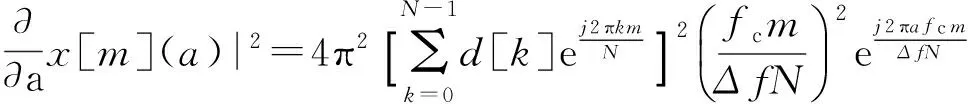
(22)

由式(22)可知，对于多普勒因子估计的CRB主要由复数信号和采样的点数所决定。采样点数越大，CRB越小。

3　系统仿真分析

3.1仿真参数

通过计算机仿真验证上述关于多普勒频移最大似然估计新算法的性能。设水声信道的最大时延扩展为l ms，这一时延与1～5 km范围内的浅水信道的实际通信情况是相符合的。系统仿真部分参数详细说明，参见表1。

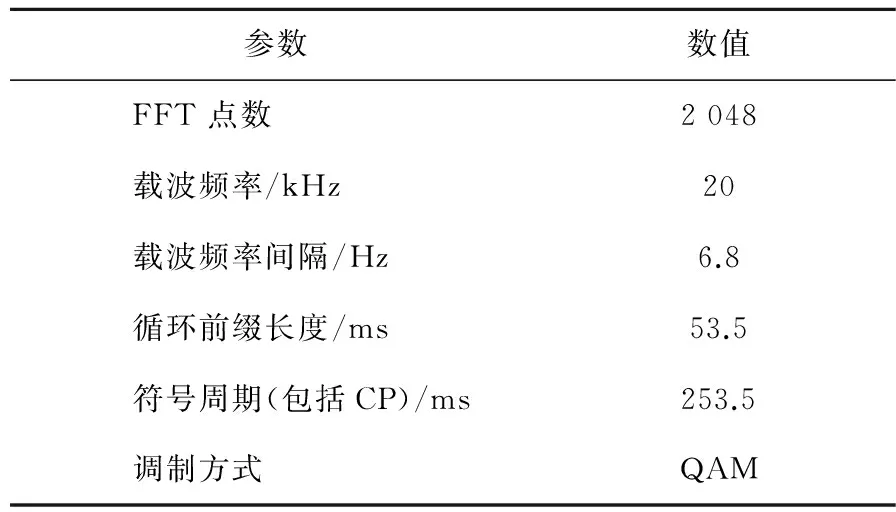
表1　OFDM系统仿真主要参数

该仿真系统载波中心频率设为20 kHz，所能处理的最大多普勒频移为40～80 Hz。这个数值相当于相对运动速度为6～12 kn的发射机与接收机之间所产生的多普勒频移。仿真系统平均分配所有子载波的功率和频率间隔。为了简化研究过程，文中仿真过程采用非编码方式，多径数据采用表2数据[15]。

表2水声信道多径幅度衰落和相对时延

Table 2Amplitude fading and relative delay related with multipath in UWA channel

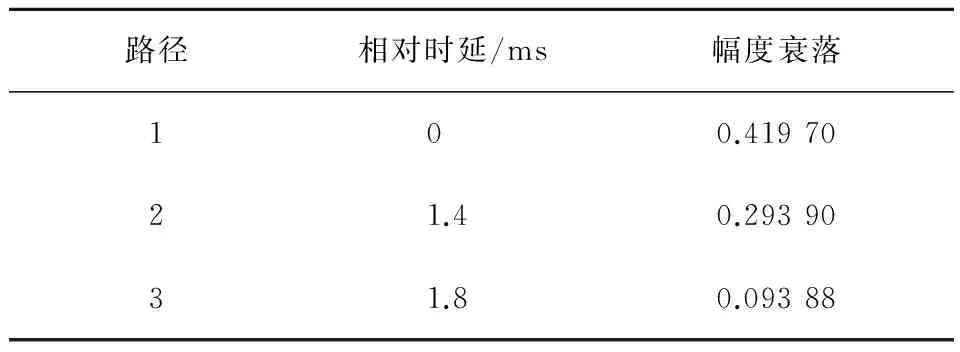
路径相对时延/ms幅度衰落1 00.419702 1.40.293903 1.80.09388

3.2多普勒频移对误码率的影响

采用表2数据对此进行了仿真，分别采用1径信道和3径信道进行研究。结果表明，对于一定子载波数的OFDM水声通信系统，存在一个多普勒频移的临界值，如果多普勒频移超过此值，OFDM信号中携带的有效信息就会受到破坏。仿真结果如图2所示，在系统FFT点数为2 048，载波频率为20 kHz的情况下，当多普勒因子达到3×10-5时，系统的误码率已经超过了10-2。另外，在多径情况下，多普勒频移对于系统误码率的影响也是有所上升的。

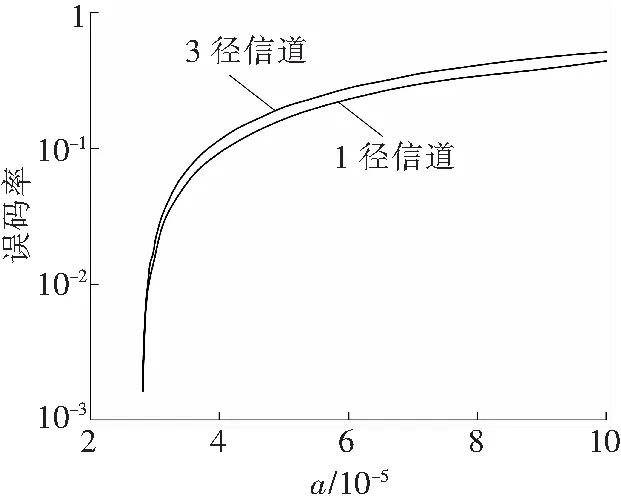
图2　多普勒频移对误码率的影响

3.3最大似然值与多普勒固子的关系

设一种极限情况信噪比为0，1径信道主要受多普勒频移和加性高斯白噪声的影响，对于接收到的数据进行最大似然估计，在上述仿真系统的条件下，如图3所示，当多普勒因子a=0.003时，似然函数达到最大值。对于3径信道，主要采用表2中的数据，在这种情况下，得到的似然函数最大值所对应的多普勒因子依然近似为a=0.003，这说明最大似然估计法，对于同一OFDM发射系统，在不同路径数信道的情况下，对于多谱勒频移的估计存在一致性。

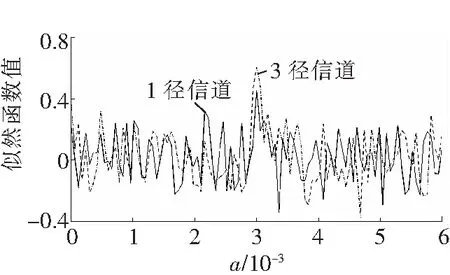
图3　最大似然函数值与多普勒因子的关系

Fig.3Relationship of maximum likelihood function and Doppler factor

3.4估计方差与低信噪的关系

首先通过仿真得到克拉美罗界，然后在1径信道和3径信道的情况下分别得到多普勒因子的估计方差与信噪比的关系曲线。图4表示的是信噪比较低的情况，当多普勒因子的数量级为10-5时，可近似认为估计方差的数量级为10-10。从图4可以看到，这时克拉美罗界线上所对应的信噪比大约为-15 dB，又根据图2的结论，这一信噪比也是系统的临界值(这一临界值会随信号和多普勒因子的改变而发生变化)。从图4中的1径信道和3径信道曲线也可以看出，当系统的信噪比低于上述临界值时，多普勒因子的估计方差会大幅上升。另外，图5中高信噪比曲线也表明在信噪比从-15～0 dB之间，多普勒因子的估计方差的变化规律基本遵从克拉美罗界。当信噪比高于0 dB时，估计方差会出现地板效应。这时估计方差会逐渐高于克拉美罗界。这种情况主要与极值搜索算法有关，此文不做详细讨论。

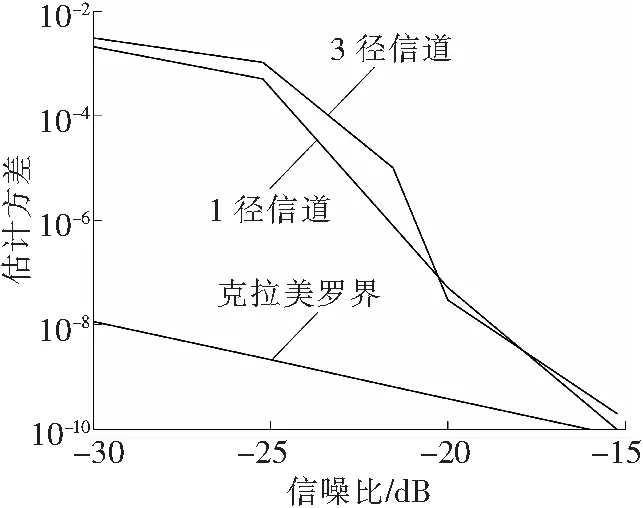
图4　估计方差与低信噪比的关系

图4和图5中多普勒因子的估计方差与信噪比的关系，也可以用图6的星座图更加直观地加以说明。由图4可见，多径现象对于多谱勒因子方差的影响可以暂不考虑。图6a和6b说明在信噪比-22 dB和-20 dB之间存在一个多普勒因子的临界值，对于这个系统只要多普勒频移超过这个临界值，系统的误码率就会急剧上升。对于图6c和6d，信噪比分别为-10 dB和5 dB,说明多普勒频移在此段信噪比区间对于系统的误码率的影响程现缓慢变化关系。

图5　估计方差与高信噪比的关系

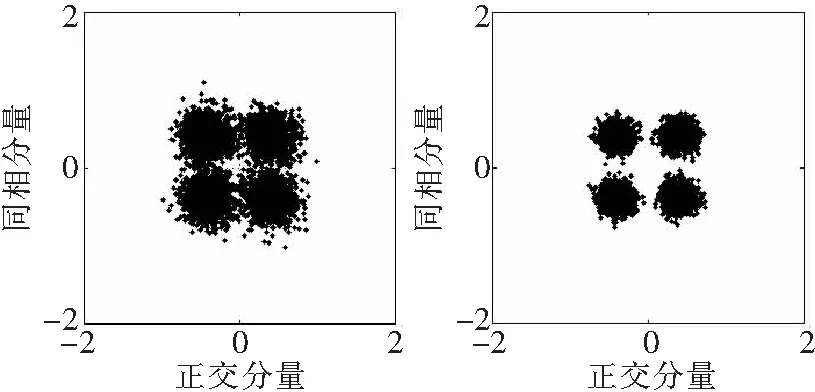
a　信噪比-22 dB　　　　　b　信噪比-20 dB

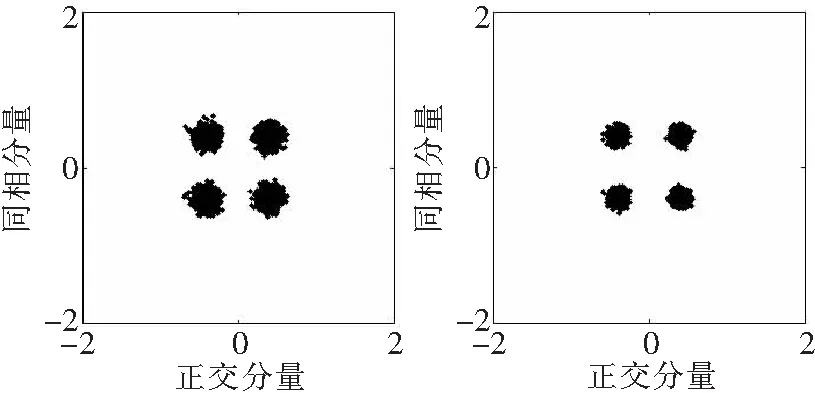
c　信噪比10 dB　　　　　d　信噪比5 dB

4　结　论

结合水声信道的特点，分析OFDM水声通信系统多普勒频移理论模型，采用最大似然的方法对多普勒频移进行估计。计算机仿真验证了最大似然估计法，给出了最大似然估计方差的下限——克拉美罗界，将多普勒因子的估计方差与克拉美罗进行了比较，得出：

(1)最大似然估计方法可以用来初步判定系统的多普勒频移的临界值。

(2)对于某一OFDM水声通信系统，存在多普勒因子估计方差最接近于克拉美罗界的信噪比范围。

(3)在不同路径数的情况下，最大似然估计法对OFDM水声通信系统多普勒因子估计具有一致性。

[1]YERRAMALLI S,STOJSNOVIC M,MITRA U.Partial FFT demodulation:A detection method for highly doppler distorted OFDM systems[J].Signal Processing IEEE Transactions on,2012,60(11):5906-5918.

[2]TU K,DUMAN T M,STOJAOVIC M,et al.Multiple-resampling receiver design for OFDM over doppler-distorted underwater acoustic channels[J].IEEE Journal of Oceanic Engineering,2013,38(2):333-346.

[3]MA L,QIAO G,LIU Q.Doppler estimation based on two identical OFDM symbols in underwater acoustic communications[C]// Xianning:CECNet,2014:55-64.

[4]SHARIF B S,NEASHAM J,HINTON O R,et al.A computationally efficient Doppler compensation system for underwater acoustic communications[J].Oceanic Engineering,IEEE Journal of,2000,25(1):52-61.

[5]BEAUJEAN P P,LEBLANC L R.Adaptive array processing for high-speed acoustic communication in shallow water[J].Oceanic Engineering,IEEE Journal of,2004,29(3):807-823.

[6]MASON S,BERGER C,ZHOU S,et al.Detection,synchronization,and Doppler scale estimation with multicarrier waveforms in underwater acoustic communication[J].Selected Areas in Communications,IEEE Journal on,2008,26(9):1638-1649.

[7]张翔.水声通信中多普勒频移补偿的仿真研究[J].系统仿真学报,2005,17(5):1172-1174.

[8]崔健,黄建国.OFDM 水声通信中的综合多普勒补偿方法[J].计算机工程与应用,2008,44(1):129-131.

[9]常娟,王海燕,申晓红.OFDM 水声通信中最大多普勒频偏估计算法研究[J].无线通信技术,2007,16(3):37-40.

[10]LI B,ZHOU S,STOJANOVIC M,et al.Multicarrier communication over underwater acoustic channels with nonuniform Doppler shifts[J].Oceanic Engineering,IEEE Journal of,2008,33 (2):198-209.

[11]DAOUD S,KARAKAYA B,GHRAYEB A.Doppler compensation for AF two way relaying over time varying UWA channels[C]// Istanbul,Turkey:Institute of Electrical and Electronics Engineers Inc,2014:1082-1086.

[12]陈阳,张艺朦,赵安邦,等.两种 OFDM 多普勒估计算法在水声信道中的比较[J].吉林大学学报：信息科学版,2012(4):341-346.

[13]徐小卡.基于 OFDM 的浅海高速水声通信关键技术研究 [D]:哈尔滨：哈尔滨工程大学,2009.

[14]郭铁梁,赵旦峰,杨大伟.正交频分复用水声通信系统多普勒频移快速估计[J].吉大学报：工学版，2013(3):813 -818.

[15]邓红超,刘云涛,蔡惠智.瑞利分布时变水声信道仿真与实验[J].声学技术,2009,28(2):109-112.

(编辑晁晓筠)

Maximum likelihood estimation for Doppler shift of OFDM underwater acoustic communication

GUO Tieliang，REN Dunliang，HAO Juncai，JIANG Hongxi

(School of Sciences,Heilongjiang University of Science &Technology,Harbin 150022,China)

This paper proposes an improved method capable of estimating and compensating the Doppler effects at the receiving end,an approach designed for working with the metabolic time,space and frequency of underwater acoustic(UWA) channel,and above all overcoming the notorious effect on the orthogonality among subcarriers by the Doppler frequency shift resulting from the relative motion between transmitters and receivers.The proposed method building on the OFDM data block and on the assumption that Doppler factor does not change with the path during one block works by estimating the Doppler frequency shift using the maximum likelihood estimation algorithm;providing the simulation analysis of the critical value of Doppler factor,combined with the maximum likelihood algorithm;and ultimately comparing the variance of the factor with the Cramer Rao bound(CRB).The results show that the system features a rang of SNR(-15—0 dB provided in this paper),allowing the estimation variance to be the most close to the CRB.The method capable of giving the threshold value of Doppler shift,and thereby ensuring the consistency of the estimated parameters in different channel conditions could contribute to an improvement in the estimation precision of Doppler factor.

underwater acoustic communication;orthogonal frequency division multiplexing;Doppler shift;maximum likelihood estimation;Cramer Rao bound

2016-05-01

黑龙江省自然科学基金项目(F2015018)

郭铁梁(1971-),男,黑龙江省双城人,副教授,博士,研究方向：现代通信系统与通信技术，E-mail:guotieliang@hrbeu.edu.cn。

10.3969/j.issn.2095-7262.2016.03.015

TN929.3

2095-7262(2016)03-0304-07

A