主动式波浪补偿在位置控制系统中的应用

鄢华林，缪 鑫，王 伟，程 浪

（江苏科技大学，镇江 212003）

主动式波浪补偿在位置控制系统中的应用

鄢华林，缪 鑫，王 伟，程 浪

（江苏科技大学，镇江 212003）

为确保海洋作业时人及货物的安全，船体之间保持随动，为克服波浪影响，从而提出了主动式波浪补偿位置控制方法。首先，建立主动式波浪补偿电机驱动系统的数学模型；然后采用智能伪微分控制控制算法，实现整个位置控制系统的仿真，其响应效果完全满足系统的要求，构建实验平台。实验结果与仿真结果一致，验证了此法的可行性。

主动式波浪补偿；位置控制；伪微分控制器

0　引言

在海上作业时，因为作业环境相对复杂，海风、海浪以及船舶自身的航行会使相对作业的船舶之间产生相对运动，引起货物碰撞甲板或者货物悬空，从而造成甲板与货物的碰撞产生损坏或者缆绳因张力过大而断裂带来更严重的安全问题。为解决上述出现的这一系列安全问题，提出了主动式波浪补偿这个概念。本文将主动式波浪补偿应用到位置控制中，能及时预测并做出正确的应对措施来减少损失规避风险。

1　主动式波浪补偿的原理

本文是运用主动式波浪补偿的原理，将其应用在海洋作业时的位置控制上，主要是由控制系统、电机系统以及执行系统组成的。若想在海洋平台上实现安全平稳的作业，就必须补偿因波浪、船舶自身的航行和其他因素造成两船舶之间的相对运动，此时所需要的位置补偿如图1所示。

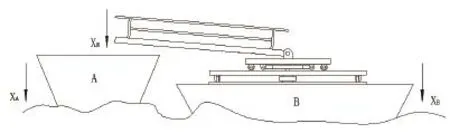
图1　位置控制补偿原理

从图1可知船A位移量为xA，船B位移量为xB，电机控制的货物位移量为xM，这时候可以设货物与船A的相对位移为xAM，位置控制的目的就是保证货物与甲板相对距离为恒定值即xAM=C，式中C为常数。

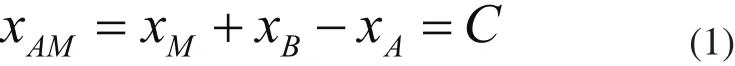
驱动系统选择的是电机驱动，其电机选型为稀土永磁直流伺服电机，其直流伺服电机驱动系统如图2所示。

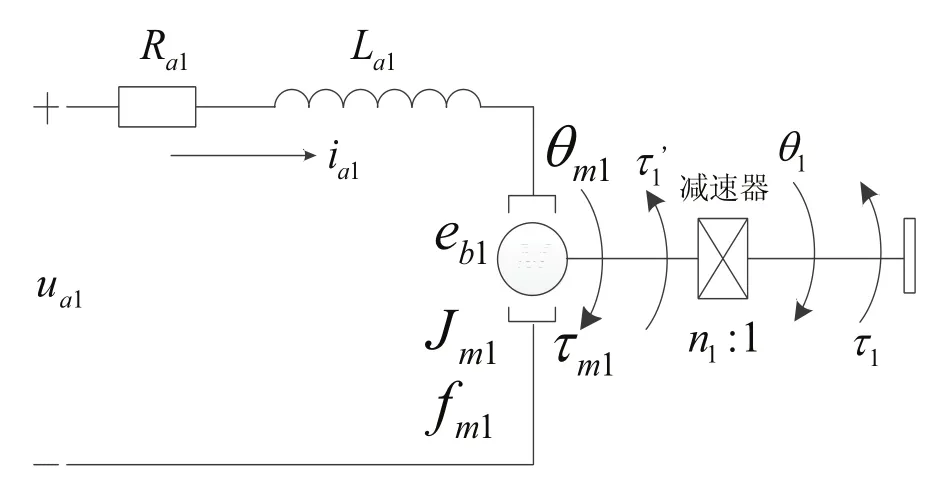
图2　直流伺服电机驱动系统

2　位置控制驱动系统的数学模型建立

2.1电机数学模型的建立

根据力学性质和电路的基本定律得出电机驱动系统的微分方程。

对于电机驱动系统根据基尔霍夫电压定理有方程：

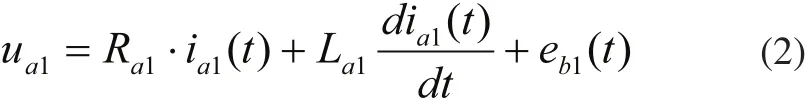
式（2）中eb1（t）是反电动势，满足下式：

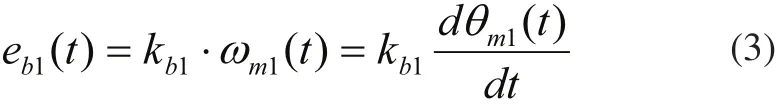
电机的驱动力矩与电流成正比关系，即：

根据直流电机轴上受力情况可以列出如下方程：

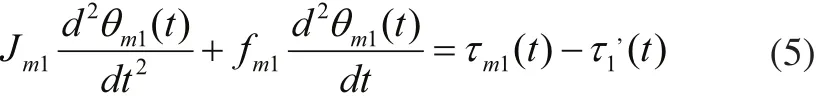
其中：

kb1和k1分别为为稀土永磁直流电机的反电动势常数和力矩常数；

Jml和fml分别为折合到直流伺服电机输出轴上等效转动惯量与等效粘性摩擦系数；

τm1和分别为直流伺服电机产生的驱动力矩与作用在输出轴上的阻抗力矩；

可以把直流伺服电机看作理想状态，经过减速器后，并没有产生相应的能量损失，由上式可得：

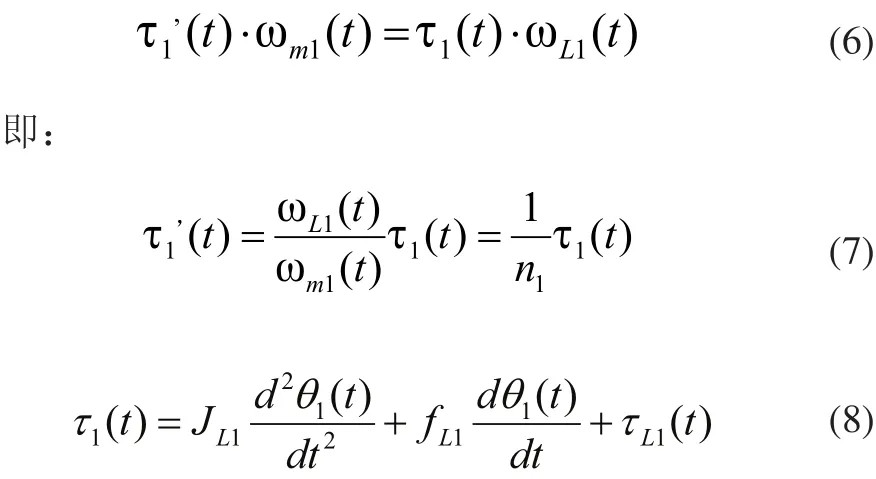
其中：

JL1和fL1分别为负载的等效转动惯量和等效粘性摩擦系数；

τL1（t ）为其他干扰因素。

由式（6）、式（7）和式（8）可以得到：

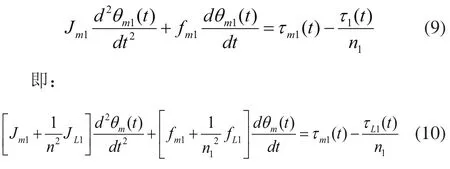
将其折算到稀土永磁直流伺服电机的输出轴上，可以得到：

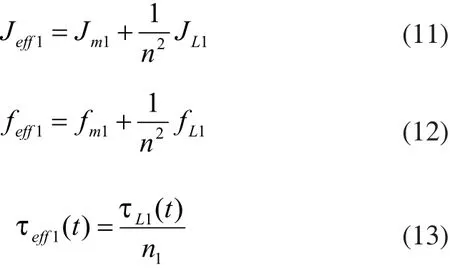
其中：

Jeff1、feff1和τeeffff11分别为折算到输出轴上的总等效转动惯性量、等效阻尼系数和等效干扰力矩。

因此，式（12）可简化为：

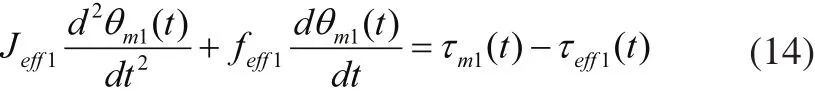
将式（2）、式（3）、式（4）和式（14）进行Laplace变换得：

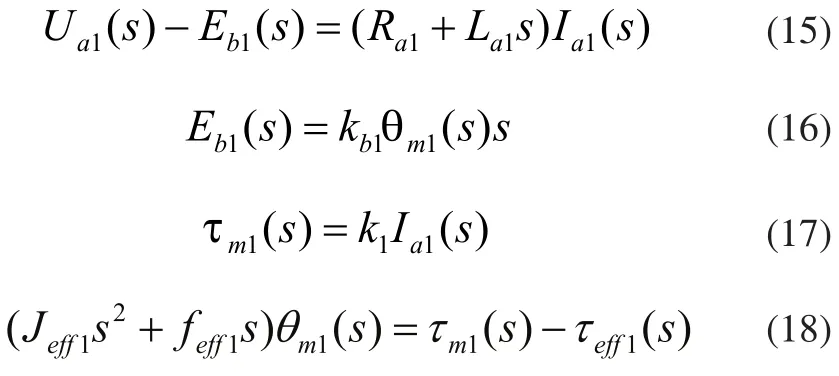
2.2传递函数的建立与简化

根据式（15）、式（18）可以得出直流伺服电机驱动系统的结构框图，如图3所示。

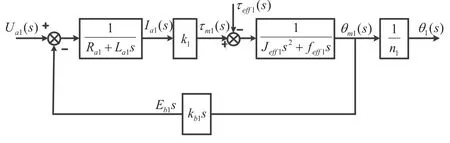
图3　伺服电机传递函数方框图

由图3可得：

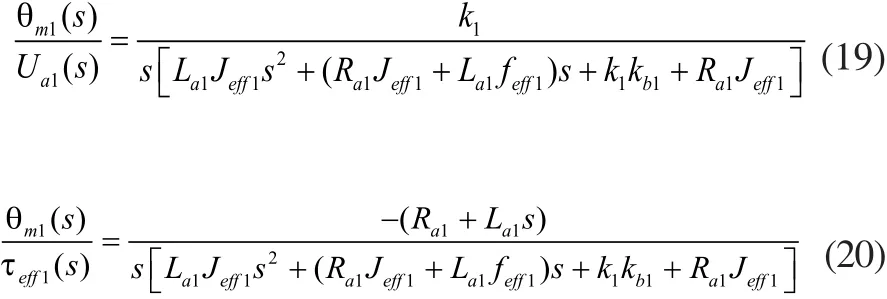
于是有：

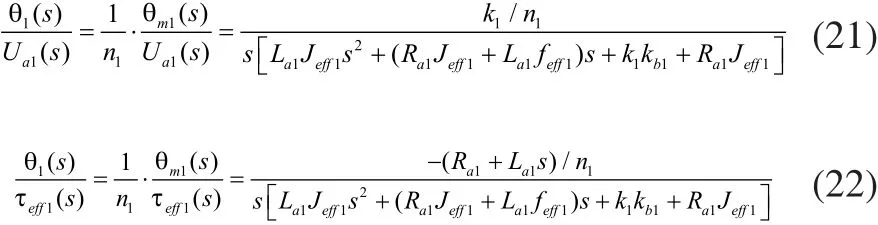
由于在直流伺服电机电枢电路中，电感值La1通常为零点几毫亨级，所以在建模的过程中可将电感值忽略不计，可对传递函数进行简化可得：

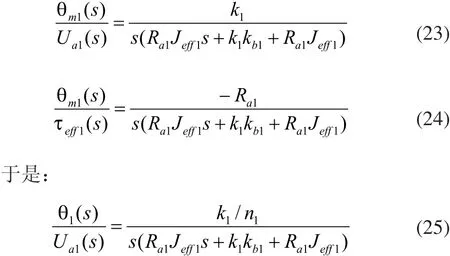
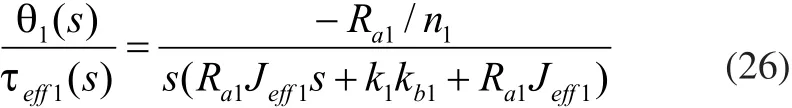
通过对传递函数的观察可以发现直流电机位置控制的传递函数系统没有零阶相，故系统的本身是不稳定，简化为二阶系统后的一般形式为：

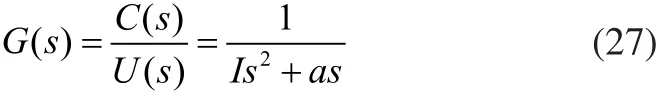
带入该直流伺服电机系统相关参数，其传递函数为：

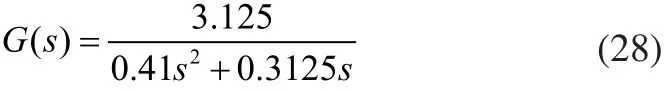
3　智能伪微分控制器

伪微分反馈控制控制器（Pseudo－Derivative－Feedback）是从微分反馈控制控制器改进而来，又称PDF算法。经过上述传递函数推导可知，主动式波浪补偿位置控制电机驱动系统属于二阶被控对象系统，其微分反馈控制系统的结构框图如图4所示。

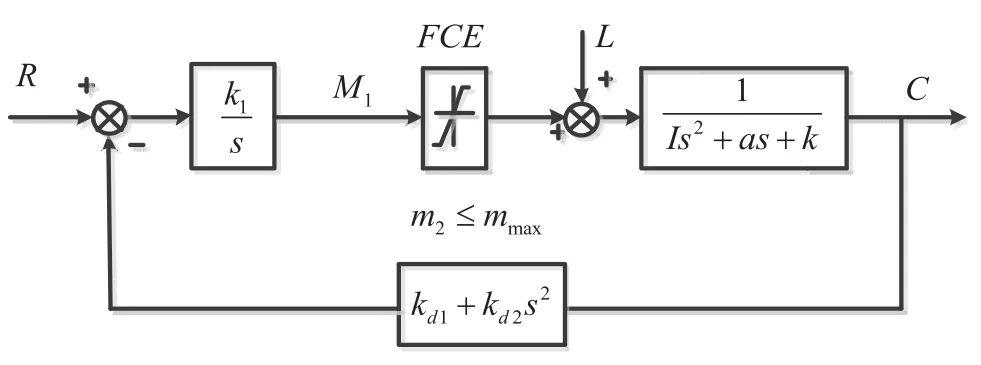
图4　微分反馈控制器

由图4可知，输出信号C先后经过微分和积分运算，两次运算后的结果依旧为C，所以主反馈回路对输出信号C的微分是无效的。采用微分反馈控制算法时，不可避免的增加对参考输入的运算，从而会在系统微分方程的右侧产生相应的强迫项，会降低系统的响应速度。

针对响应速度的问题，对图4进行修改，得到新的系统框图，所得结果如图5所示。

比较图5和图4可得，修改后反馈回路中微分阶次降了一阶，而且主反馈回路并没有对被控量直接进行微分运算，经计算可得出两种控制算法对M1（t）输出方程相同，为：

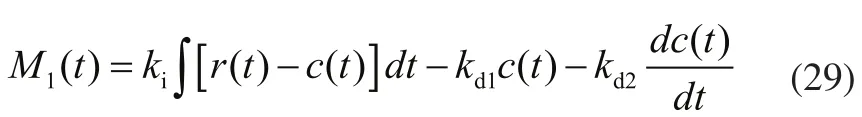
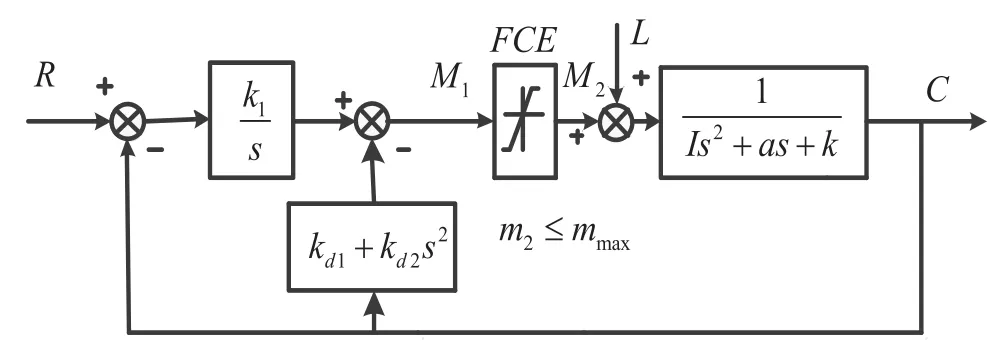
图5　PDF控制系统方框图

由式（29）可知，改进后的控制框图和开始的控制框图的输出信号相同，所以称之为伪微分反馈控制。实际运算时，因为伪微分反馈控制的微分运算低于微分反馈控制运算，在保证输出不变的情况下，减少了微分反馈对噪声信号的增益，有效提高了控制品质，大大的提高了响应速度。

经过整定，可以确定Ki、Kd1、Kd2的计算公式：

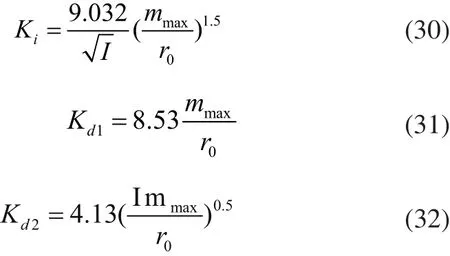
其中：mmax为输出单元在线性范围内所能的最大值；r0为输出信号在线性范围内的最大值。

4　基于伪微分控制器下系统仿真与结果分析

4.1参数设定及仿真

主动式波浪补偿应用在位置控制方面，其试用范围应在4级海浪以下，由表1可知，四级海浪的波高为2.0m。

调试Ki、Kd1、Kd2三个参数对系统控制要求的影响，使其进行调试后能达到预期的理想控制效果。根据式（30）、式（31）、式（32）可得出参数大小，参数值如表2所示。

表1　海浪等级表

表2　伪微分控制参数表

因为主动式波浪补偿位置控制是针对于海洋平台的，其运作环境为海上作业，在海上运作时势必会受到海浪的影响，而波浪运动是周期往复的，近似于正弦波，所以在系统仿真的时候，一般会选取正弦波信号作为波浪信号。此时可以MATLAB中的Simulink里建立PDF（伪微分）控制器传递函数方框图，如图6所示。

4.2仿真结果分析

主动式波浪补偿应用在位置控制方面，其波浪周期也就是正弦波的周期约为7秒，波浪运动的幅值一般能达到2.0m。系统的仿真响应曲线如图7所示。

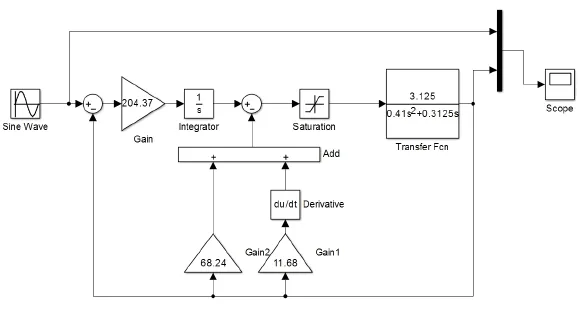
图6　PDF控制Simulink的仿真框图

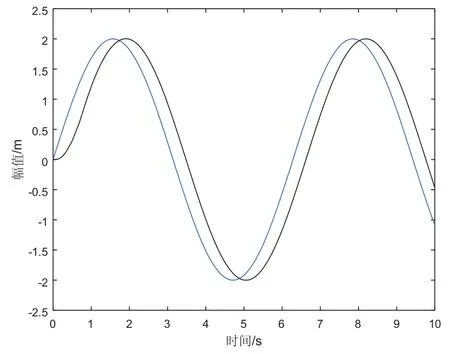
图7　电机驱动正弦曲线

从仿真后的图7可以看出，主动式波浪补偿系统对于波浪（即正弦波）的响应与给出的正弦波信号基本保持一致，能达到了主动式波浪补偿控制系统对于响应性的要求。

5　实验平台的搭建与实验结果

5.1实验平台的搭建

为验证所提方法的有效性，搭建了主动式波浪补偿在位置控制中应用的模型 ，如图8所示。

图8　模型的实物图

上述实验平台搭建所需的实验设备如表3所示。

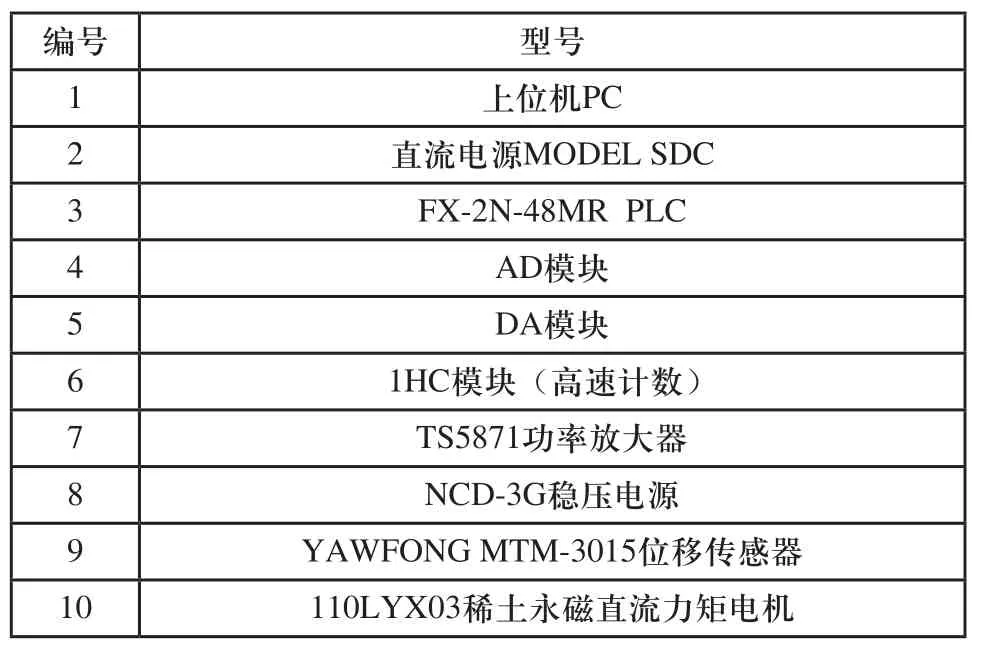
表3　实验设备表

5.2实验结果

实验结果所得的跟随曲线如图9所示。

【】【】

Application of active wave compensation in the position control system

YAN Hua-lin， MIAO Xin， WANG Wei， CHENG Lang

TP273

A

1009-0134（2016）10-0029-04

2016-05-12

鄢华林（1957 -），男，江西高安人，研究员，博士，研究方向为电液伺服控制和海洋装备。