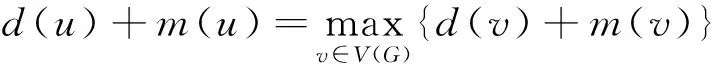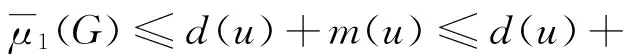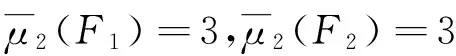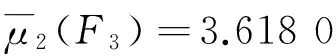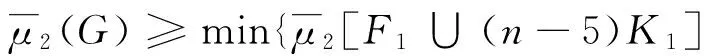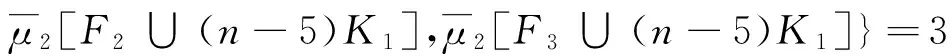单圈图的最大拉普拉斯分离度
黄冬明,方 怡,余桂东
(安庆师范大学 数学与计算科学学院,安徽 安庆 246133)
单圈图的最大拉普拉斯分离度
黄冬明,方怡,余桂东
(安庆师范大学 数学与计算科学学院,安徽 安庆 246133)

单圈图;图的拉普拉斯分离度;图的拉普拉斯矩阵
设G=(V(G),E(G))是一个n阶简单连通图,其顶点集V(G)={v1,v2,…,vn},边集E(G)={e1,e2,…,em}。若m=n,则称G是单圈图。通常情况下,用Kn、K1,n-1、Cn、Pn分别表示n个顶点的完全图、星图、圈和路。
下面给出相关引理。


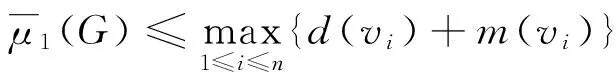

假设G1和G2是两个顶点集不相交的图,其中v1∈V(G1),v2∈V(G2),图G1和G2的粘图记为G1·G2,其中V(G1·G2)=V(G1)∪V(G2)∪({v*}-{v1,v2}),G1·G2中的两个顶点相邻,当且仅当它们在G1或G2中相邻,或者,如果一个顶点是v*,则另一个顶点和v1或v2相邻。
用Lv(G)表示由L(G)删掉顶点v相应的行和列后所得的主子矩阵。为了方便,记
Φ(G;x)=det[xI-L(G)],
Φ[Lv(G);x]=det[xI-Lv(G)]。
引理4[6]设G1·G2如上述所定义,则有Φ(G1·G2;x)=Φ(G1;x)Φ[Lv2(G2);x]+Φ(G2;x)Φ[Lv1(G1);x]-xΦ[Lv1(G1);x]Φ[Lv2(G2);x]。
图1为n阶最大度为n-1的单圈图Un。
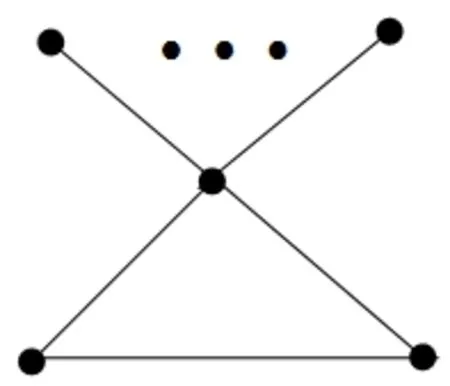
图1 Un
通过简单计算,得到下面的结论:
引理5Φ(K1,n;x)=x(x-n-1)(x-1)n-1,Φ[Lv2(K1,n);x]=(x-1)n,其中v2是K1,n的中心;Φ(C3;x)=x(x-3)2,Φ[Lv1(C3);x]=(x-1)(x-3),其中v1是C3的某个顶点。
引理6设Un如图1所示,则当n≥5时,SL(Un)=n-3。
证明将Un看作由C3的某个顶点v1和K1,n-3的中心点v2所粘合得到的图,由引理4与引理5可得
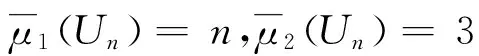
用g(G)表示图G中最短圈的长度,Δ(G)为图G的最大度,An表示n阶单圈图的集合。图2中F1、F2、F3为3个g(G)=3的5阶单圈图。
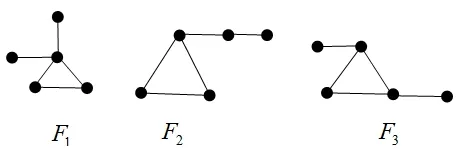
图2 F1、F2和F3
下面是本文的主要结论。
定理1设G是An中的任意一个图,则当n≥8时,有SL(G)≤SL(Un),当且仅当G=Un等号成立。
证明若G∈An,且Δ(G)=n-1,则G=Un,则结论成立。
下面证明当G∈An,且Δ(G)≤n-2时,有
SL(G) (1) (2) (3) 由(1)式和(3)式,可得 下面将分2种情形来讨论:当g(G)=3时,F1∪(n-5)K1,F2∪(n-5)K1或F3∪(n-5)K1中的某个图是G的生成子图。通过计算可得 (4) 这样由引理2可得 [1]YouZF,LiuBL.ThesignlessLaplacianseparatorofgraphs[J].ElectronicJournalofLinearAlgebra, 2011, 22: 151-160. [2]LiJX,CheeW,ChanWH.SomeresultsontheLaplacianeigenvaluesofunicyclicgraphs[J].LinearAlgebraAppl, 2009, 430(8/9): 2080-2093. [3] 简相国,袁西英,张曼. 单圈图和双圈图的最大无符号拉普拉斯分离度[J]. 运筹学学报, 2015, 19(2): 9-104. [4]CvetkovicDM,DoobM,SacksH.SpectraofGraphs:TheoryandApplications[M].NewYork:AcademicPress, 1979. [5]MerrisR.AnoteonLaplaciangrapheigenvalues[J].LinearAlgebraAppl, 1998, 285: 33-35. [6]YuanXY.ANoteonthelaplacianspectralradiiofbicyclicgraphs[J].Advancesinmathematics, 2010, 6: 703-708. The Maximum Laplacian Separator of Unicyclic Graphs HUANG Dong-ming, FANG Yi, Yu Gui-dong (School of Mathematics and Computation Sciences, Anqing Normal University, Anqing, Anhui 246133, China) unicyclic graph; the Laplacian separator of graph; Laplacian matrix 2016-03-01 安徽省高校自然科学基金(KJ2015ZD27,AQKJ2015B010)。 黄冬明,男,安徽含山人,安庆师范大学数学与计算科学学院硕士研究生,研究方向为图论。E-mail: 719004685@qq.com http://www.cnki.net/kcms/detail/34.1150.N.20160817.1131.006.html O157.5 A 1007-4260(2016)03-0018-03 10.13757/j.cnki.cn34-1150/n.2016.03.006